石英振梁加速度计静态输入输出特性
2014-07-20杨贵玉李庆丰
杨 挺,杨贵玉,李庆丰
(航天长征火箭技术有限公司,北京 100076)
石英振梁加速度计静态输入输出特性
杨 挺,杨贵玉,李庆丰
(航天长征火箭技术有限公司,北京 100076)
通过平衡方程建立了一种石英振梁加速度计敏感元件的静力学模型,分别利用梁弯曲振动微分方程和有限元分析方法获得了敏感元件的输入加速度与输出频率之间的精确关系,从而从理论上获得了敏感元件的静态输入输出特性。通过离心试验对所设计的加速度计进行了标定,并与理论计算结果进行比对,最终认为理论计算能够准确的反映出石英振梁加速度计的静态输入输出特性。同时,该计算方法可以为其他包含振梁的传感器的设计提供依据。最后,提出了实测结果与理论计算存在偏差的原因:标度因数的偏差来源于振梁厚度的加工误差,非线性度的偏差来源于装配角度偏差以及外界温度变化引起的频率漂移等因素。
静态输入输出特性;石英振梁加速度计;振动微分方程;有限元分析
石英振梁加速度计是一种利用压电谐振式测量原理,将被测加速度转换成石英振梁固有频率变化的传感器[1],因其具有大量程、高精度、小体积、低功耗、直接频率输出等优势在低成本组合导航系统、天线平台稳定系统、石油钻井等领域有着广泛的应用[2-3],其典型产品为美国 Honeywell公司的 RBA500[4]和法国Thales公司的A100[5]。
研究静态输入输出特性不仅可以深入了解石英振梁加速度计的敏感原理,同时可以获得其标度因数和线性度指标。标度因数反映了传感器的输出对输入加速度的敏感能力;而线性度则反映了加速度计的实际静态校准曲线与参考直线的吻合程度,良好的线性特性保证了测试系统解算输入加速度值的准确性。文献[6-7]中虽然均给出了梁振动轴向力与频率关系的计算方法,但是只针对单梁或是双梁石英谐振器结构,并没有将其与敏感元件整个结构结合进行分析,未给出输入加速度与振梁谐振频率的准确关系。
本文建立了目前所研制的石英振梁加速度计敏感元件的静力学模型,利用平衡关系,建立了输入加速度与梁轴向力的关系,再结合梁振动微分方程,获得了敏感元件的输入输出特性关系的解析表达式;建立了敏感元件的有限元模型,利用ANSYS软件中包含预应力的模态分析功能,同样获得了敏感元件的输入输出曲线;最后,通过离心试验测得所研制石英振梁加速度计的实际静态校准曲线,并与前面的理论计算结果进行比较,最终验证了理论计算的结果。该理论分析方法可以为其它振梁式传感器的敏感元件设计提供参考。
1 敏感元件静力学分析
1.1 敏感元件静力学模型
石英振梁加速度计敏感元件的结构示意图如图1所示,主要包括振梁、挠性支撑摆和质量摆。振梁为单梁形式,振动方式为Z平面内弯曲振动,当有Z向的加速度输入时,质量摆绕挠性支撑摆中心转动,从而在振梁内部引入轴向力,这里假设振梁和挠性支撑摆为柔性结构,忽略其自身质量,而质量摆当成刚体处理,质量为m。
以敏感元件感受到+Z向的加速度a为例进行分析,如图2所示,以虚线框内的系统作为研究对象,当系统处于静止状态时,由振梁、挠性支撑摆和质量摆构成的系统应满足合力和力矩为零,令挠性支撑摆质心为支点,由此可以获得如下平衡方程:

图1 敏感元件结构示意图Fig.1 Schematic diagram of the sensing element

图2 敏感元件静力学模型Fig.2 Schematic diagram of the static model
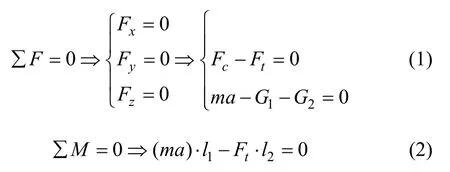
式(1)中,Ft为振梁所受到的轴向拉力,Fc为挠性支撑摆受到的轴向压力,G1和G2分别为振梁内部节点和挠性支撑摆质心所受到的Z向的剪切力。由于系统处于非惯性系下的静止状态,必须考虑外界加速度a引起的惯性力ma。式(2)中l1为质量块质心到支点的Y向距离,即惯性力ma的力臂;l2为振梁与支点的Z向间距,即Ft的力臂。
从式(1)可以看出,当系统感受到外界输入时,振梁与挠性支撑摆受到的轴向力大小相等,方向相反,而由式(2)可以建立振梁所受轴向力与外界加速度的关系,即:

式中,l1/l2可以称为杠杆的放大倍率,反映了敏感结构对于外界加速度的放大能力。同时,式(3)表明振梁内部的轴向拉力与外界输入加速度成正比。事实上,如果输入加速度方向为-Z向,也将得出类似的结论,只是此时振梁内部的轴向力将以压力形式存在,轴向压力与输入加速度的关系仍满足式(3)。
1.2 梁弯曲振动方程
前一部分已经获得输入加速度a与轴向力F的关系,而若要获得敏感元件的输出频率f,还必须建立轴向力与振梁谐振频率的关系,这就必须借助于梁弯曲振动方程。对于图3所示的双端固定单梁,在轴向力作用下,梁的横向弯曲自由振动方程为:
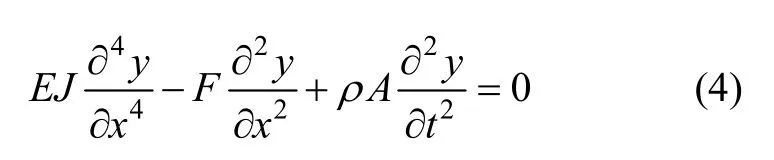
式中,E为弹性模量;J为梁的横截面在弯曲方向的惯性矩,大小为hw3/12;y为挠度,x为轴向坐标,F为梁受到的轴向力,ρ为材料密度;A为横截面积,大小为hw;t为时间。设原点在振梁左端,由于梁是两端固定,故边界条件为:
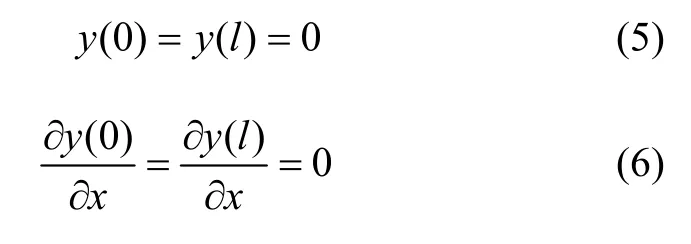

图3 双端固支梁结构示意图Fig.3 Schematic diagram of the double-clamped beam
依据边界条件式(5)和式(6)对式(4)求解即可获得轴向力与频率关系的解析表达式:
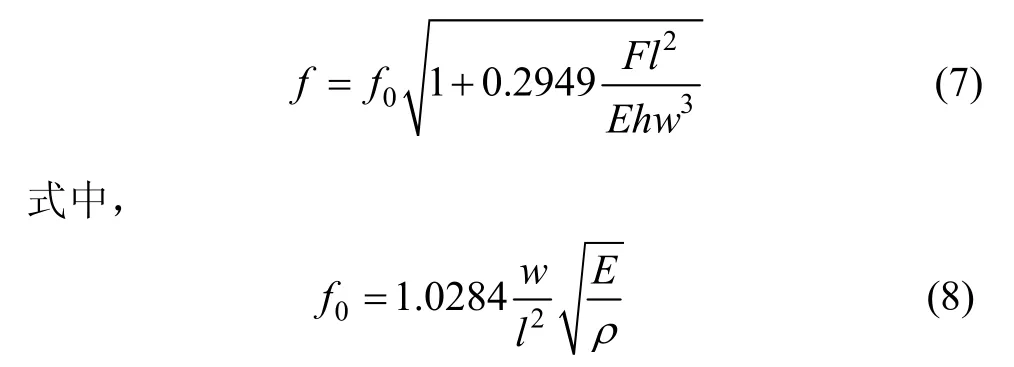
由式(3)和式(7)即可建立输入加速度a与振梁谐振频率f的关系表达式。表1为自行研制的一种石英振梁加速度计敏感元件的结构参数以及计算所需要的常数值,当输入加速度为-100g~+100g时,利用Matlab绘制式(7)的曲线图,如图4(a)所示,利用最小二乘法对该曲线进行线性拟合后可以获得单一敏感元件的标度因数(即线性拟合曲线的斜率)为23.28 Hz/g,非线性度为0.6%F.S.。
如果对式(7)进行泰勒级数展开,可以获得式(9):
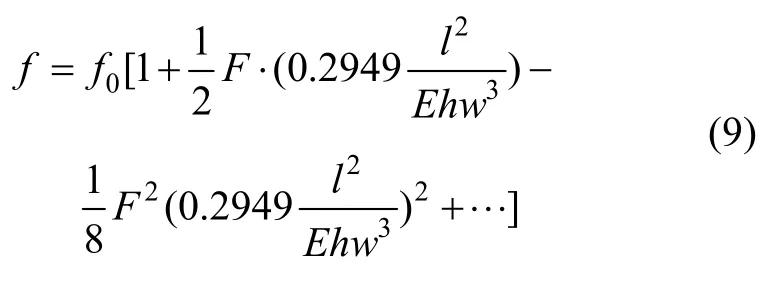
为了消除2次项误差,同时增加敏感元件的灵敏度,可以采用差分装配,即将两个敏感元件沿Z向反向放置,将二者的频率差值Δf作为敏感元件的输出,其表达式为式(10):
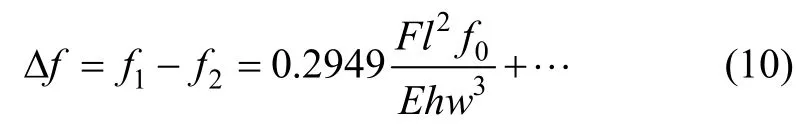
式(10)中除了1次项外,只剩下3次以上的非线性项。同样可以绘出Δf对输入加速度a的曲线图,如图4(b)所示,对该曲线进行线性拟合后可以获得差分装配后敏感元件的标度因数为46.57 Hz/g,是单一敏感元件的2倍,非线性度为0.0124%F.S.,明显小于单一元件的结果,具有更好的线性特性。

表1 敏感元件结构参数及相关常数值Tab.1 Values of configuration parameters and basic constant
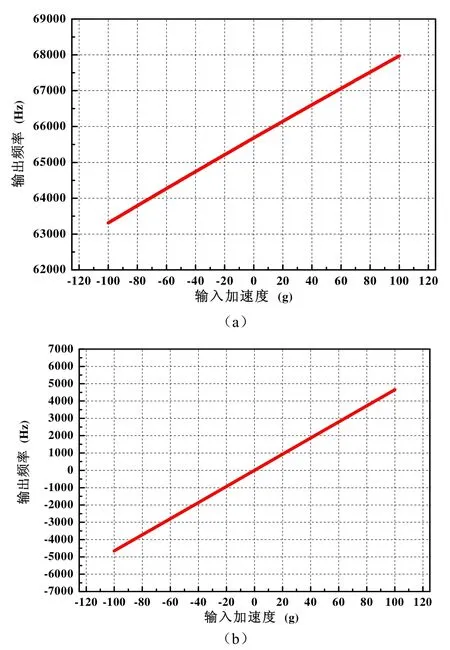
图4 静力学分析获得的敏感元件输入输出特性Fig.4 Input-output characteristics of the sensing element obtained by static analysis
2 敏感元件有限元仿真
借助ANSYS软件中包含预应力的模态分析功能同样可以获得敏感元件输入加速度a与输出频率f的关系曲线。预应力计算中,可以在Z向加载-100g~+100g的惯性载荷。图5为敏感元件结构的有限元模型,计算过程中采用10节点的四面体Solid187单元,材料参数考虑了石英的各向异性,分网采用程序控制自由网格划分,薄梁结构区域网格进行了细化,单元总数量为14 560个。

图5 敏感元件有限元模型Fig.5 Finite element model of the sensing element
经计算,单个敏感元件的加速度-频率特性如图6(a)所示。通过线性拟合得到敏感元件的标度因数为22.08 Hz/g,非线性度为0.628%F.S.。当将两个敏感元件差分装配后,敏感元件的工作特性如图6(b)所示,此时敏感元件的标度因数提高至 44.17 Hz/g,非线性度为0.0119%F.S.,与前面静力学分析的结果基本吻合。
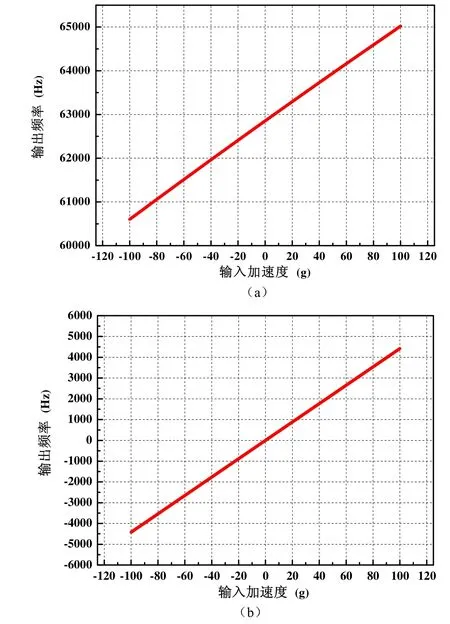
图6 有限元仿真获得的敏感元件输入输出特性Fig.6 Input-output characteristics of the sensing element obtained by finite element analysis
3 离心试验验证
为了验证前面理论分析的准确性,对所研制的样机进行了离心试验,输入加速度范围与理论计算的范围一致,即-100g~+100g。图7给出了离心试验获得的石英振梁加速度计的静态校准曲线,作为对比,同时给出了前面解析计算、有限元分析所获得的曲线。从图7中可以看出,理论计算能够基本准确地反映出敏感元件的输入输出特性。
经线性拟合分析可知,石英振梁加速度计实测标度因数为43.39 Hz/g,略低于理论计算值,与有限元分析结果的误差为 1.77%。主要原因在于敏感元件在加工过程中,薄梁是通过单面腐蚀加工而成,对其最终厚度h的控制难度较大,可能存在±5 μm左右的加工误差。由式(10)可知,如果厚度比设计值大,则标度因数将有所降低。
实测非线性度为 0.0477%,大于理论计算获得的数值,分析认为原因主要有三点:第一,实际装配的石英振梁加速度计中两个敏感元件在结构上不可能完全一致,存在一定的加工误差,无法将式(9)中的2次及以上的偶次项完全消掉,因此抑制共模误差的能力有限;第二是两个敏感元件的敏感轴在装配过程中存在角度偏差;第三是测试过程中无法保证环境温度的稳定,石英谐振器的谐振频率会随着温度变化发生漂移,从而引入非线性误差。

图7 加速度计输入输出特性曲线Fig.7 Input-output characteristics of the accelerometer
4 结 论
本文分别利用静力学方程、有限元仿真和离心试验获得了所研制石英振梁加速度计的输入加速度-频率曲线和非线性度,经对比分析认为,理论计算基本能够准确地获得敏感元件的线性特性,可以作为石英振梁加速度计结构设计的依据,同时为其它振梁式传感器设计提供参考。理论计算的标度因数值与实测值存在一定误差,原因在于薄梁厚度存在较大的加工误差;而非线性度大于实测值,主要原因是差分工作的元件结构之间存在加工误差、装配角度偏差和外界温度变化的引起的频率漂移。
(References):
[1]Levy R,Gaudineau V.Phase noise analysis and performance of the vibrating beam accelerometer[C]//2010 IEEE International Frequency Control Symposium.2010:511-514.
[2]Traon O L,Janiaud D,Guerard J,et al.The fairy world of quartz vibrating MEMS[C]//2012 European Frequency and Time Forum.2012:214-220.
[3]Levy R,Papin G.A new electronic scheme to compensate MEMS resonators nonlinearities[C]//2012 IEEE 25th International Conference on Micro Electro Mechanical Systems.2012:508-510.
[4]高延滨,詹俊妮,何昆鹏,等.高精度石英振梁加速度计频率采样系统设计[J].应用科技,2012,39(3): 61-63.GAO Yan-bin,ZHAN Jun-ni,HE Kun-peng,et al.Design of a high-precision VBA frequency sampling system[J].Applied Science and Technology,2012,39(3):61-63.
[5]Menozzi G,Pleska E.MEMS in France:an overview of trends and products for aeronautic &defense applications[R].Advances in Navigation Sensors and Integration Technology.France:NATO OTAN,2003:9.1-9.20.
[6]Zhao Chihang,He Jie,Huang Libin,et al.A novel double-ended tuning fork quartz accelerometer[C]//2011 Third International Conference on Measuring Technology and Mechatronics Automation.2011:187-190.
[7]冯丽爽,王文璞,周震,等.石英振梁加速度计谐振器的结构设计[J].中国惯性技术学报,2013,21(1):101-105.FENG Li-shuang,WANG Wen-pu,ZHOU Zhen,et al.Structure design of quartz vibrating beam accelerometer resonator[J].Journal of Chinese Inertial Technology,2013,21(1):101-105.
Static input-output characteristics for quartz vibrating beam accelerometers
YANG Ting,YANG Gui-yu,LI Qing-feng
(Aerospace Long March Launch Vehicle Technology Company,Beijing 100076,China)
The static model of a quartz vibrating beam accelerometer’s sensing element was established based on equilibrium equations.The precise relations between the input acceleration and the output frequency of the sensing element were deduced based on flexural vibration differential equation and finite element analysis.Then the static input-output characteristics of the sensing element were obtained in theory.Furthermore,the static input-output characteristics of the accelerometer were calibrated via centrifugal test.The test results were compared with the theoretical calculation results.In conclusion,the theoretical prediction can precisely reveal the static input-output characteristics of the quartz vibrating beam accelerometer.The analysis method of this paper can provide valuable references for the design of other sensors with the vibrating beam.In the end,it is pointed that there are differences between the results obtained from the centrifugal test and the calculation,in which the scale factor deviation is caused by the micro-machining error in the beam thickness and the deviation of the nonlinearity is ascribed to assembly errors,frequency shift.
static input-output characteristics;quartz vibrating beam accelerometers;vibration differential equation;finite element analysis
V 241.5;TH 824.3
A
1005-6734(2014)03-0386-05
10.13695/j.cnki.12-1222/o3.2014.03.020
2013-10-14;
2014-02-11
总装预研项目(51323040123)
杨挺(1985—),男,工程师,从事微机械加速度计研究。E-mail:andrewfine@semi.ac.cn
book=390,ebook=115
