基于改进最小二乘支持向量机的惯性测量组件故障在线检测方法

杨 辉，赵 剡，滕 冲，李 敏

（北京航空航天大学 仪器科学与光电工程学院，北京 100191）

基于改进最小二乘支持向量机的惯性测量组件故障在线检测方法

杨 辉，赵 剡，滕 冲，李 敏

（北京航空航天大学 仪器科学与光电工程学院，北京 100191）

为提高惯导系统工作的可靠性和导航性能，对其惯性测量组件的故障模式和检测模型进行了分析。针对最小二乘支持向量机（LS-SVM）回归算法做了两点改进，具体方法是先对输入样本观察窗平移更新的每个样本数据进行异常点滤波判断并用牛顿插值法进行处理，接着通过对在线LS-SVM回归过程的研究，提出了一种递推求解的快速算法，将惯性测量组件的输出量、舵偏角改变量并辅以环境因素作为观测样本序列，应用该算法来提高模型检测的准确性和时效性。最后对惯性测量组件无故障和出现卡滞、恒偏差时的故障模式进行了仿真实验，结果表明，与应用LS-SVM、SVM和BP神经网络算法相比，提出的惯性测量组件故障在线检测方法具有较强的鲁棒性和较快的速度。

惯性测量组件；在线最小二乘支持向量机；动态数据窗；鲁棒性；故障预测

惯导系统是技术密集和高度复杂的非线性动力学系统，因其工作环境特殊，同时还要考虑体积、重量等，所以不太适合应用硬件冗余的方法对其故障检测；基于神经网络的故障检测方法虽有一定成效，但在有限样本学习能力最优却并不能保证对未知样本的推广能力更好，而且易出现局部极值点和维数灾难[1-4]；基于卡尔曼滤波的方法虽然在对准与容错组合导航方面应用广泛，但它对模型的精确性要求较高，而且滤波过程涉及的复杂计算耗时比较严重，所以这两种方法均不宜用于惯性测量组件的故障在线检测。LS-SVM虽将SVM的求解从二次规划问题转化成线性方程组，提高了求解效率，但由于失去了稀疏性，当它用于动态建模时，所需的存储空间和计算量随样本数增加而增大，容易出现数据饱和与模型实效等问题[5-6]，所以在此基础上出现了许多改进算法，如动态加权LS-SVM、增量LS-SVM[7]、在线LS-SVM[8]等算法。其中文献[8]提出的方法虽然对模型结构的适时调整起到了重要作用，但这种方法在加入新样本，剔除旧样本的时候，没有考虑训练样本数据中包含的噪声和异常点，因而决策边界就会受那些靠近决策边界的异常点影响。另外，该方法在回归过程中，每次得到的都是一个时变的线性方程组，训练求解的计算量都较大，尤其是当样本数目较多时，会严重影响在线预测的速度。

为此，先对惯性测量组件的故障模式进行了研究，接着对OLLS-SVM回归算法进行了改进，最后应用改进的算法对惯性测量组件的状态观测样本数据进行修正，基于修正之后的样本序列和相应的回归模型，实现了对其故障在线检测的目的。

1 惯性测量组件的故障模式及检测模型分析

假定只考虑飞机的纵向动态飞行，设载机模型的状态方程为[9]：

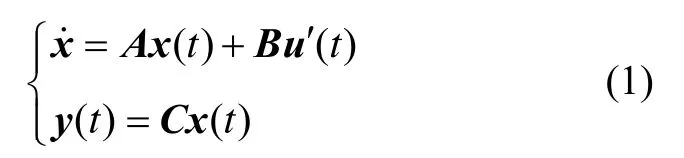
设飞机的纵向飞行控制律为：

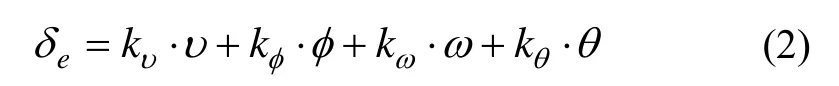
由式(2)可以看出，飞行控制律为其状态量的线性组合，因而，在装机之前对惯性测量组件进行校核尤为重要，然而受校核所用仪器及检测水平的限制，总有一些隐蔽性很强的故障被漏检，载机运行时，惯导系统基座的振动，供电电源的不稳定、环境温度、湿度的变化和空间电磁干扰等因素都可能会使这些隐蔽性很强的潜在故障发展为功能性故障，造成惯性测量组件的工作不稳定，甚至是出现故障，从而对载机飞行控制产生不利的影响。因为目前所用的惯性测量组件形式多样，不同类型的惯性测量组件因受其工作原理、制作材料、安装工艺、环境因素等影响，故障发生的模式差异较大，如果从这些影响因素方面考虑对其故障检测，不但要在载机上增加相应的硬件冗余检测装置，而且故障的分析与诊断过程极其复杂，工程领域难以应用，因此，本文将惯性测量组件（陀螺或加速度计）看作是一般的传感器，仅考虑其出现卡滞、恒增益、恒偏差和完全失效4种故障模式[10]。设u(t)为某个惯性测量组件的输入；Out(t)表示相应输出；表示对其输入信号正常时的响应输出；C、M分别为常数，K为增益系数，则其故障模式的数学描述为：

1） 卡滞故障：

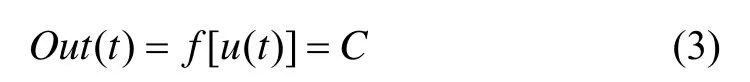
2） 恒增益故障：

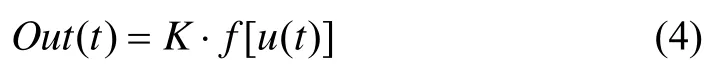
3） 恒偏差故障：

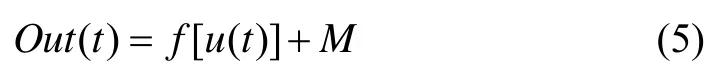
4） 完全失效故障：

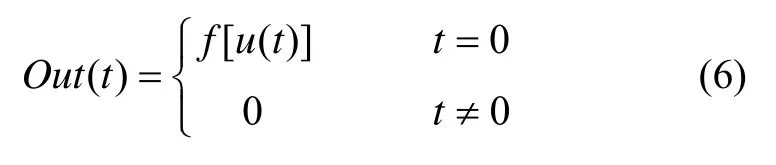
为了构建基于性能的惯性测量组件故障检测模型，需要忽略每个组件的类型，仅考虑其测量输出的原始数据υ、φ、ω θ、。由于惯导系统的潜在故障转化为功能故障是一个渐变的过程，所以在其还没有完全失效之前，可以把x(t)的各个分量、eδ及辅助因素（基座的振动量ν、环境温度T、供电电源功率P、电磁辐射χ）在k时刻的采样值放在一起构成一个时间观测阵列，用于对其故障的在线检测。惯导系统故障检测模型如图1所示。在试用过程中，为了加快在线故障检测的速度，只要采用相应的传感器对这些环境因素实时测量并和设定的工作极限值进行对比，如果惯导系统的工作状态良好，并且各个环境因素的当前测试值也没有超出其工作极限值，则忽略各个环境因素对惯导系统性能的影响，直接采用x(t)的各个分量及eδ进行预测即可，相反，则须考虑其影响。所以对于式(1)，建立如式(7)所示的LS-SVM故障预测模型[11-13]。

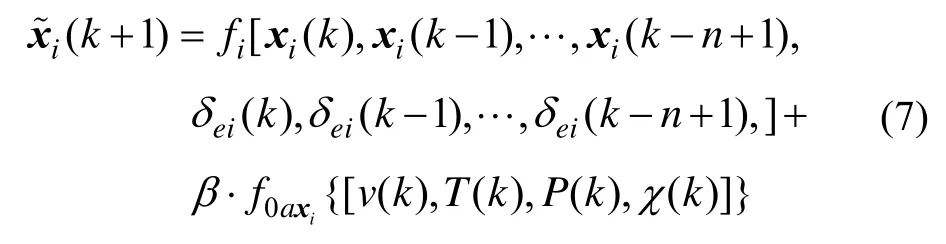
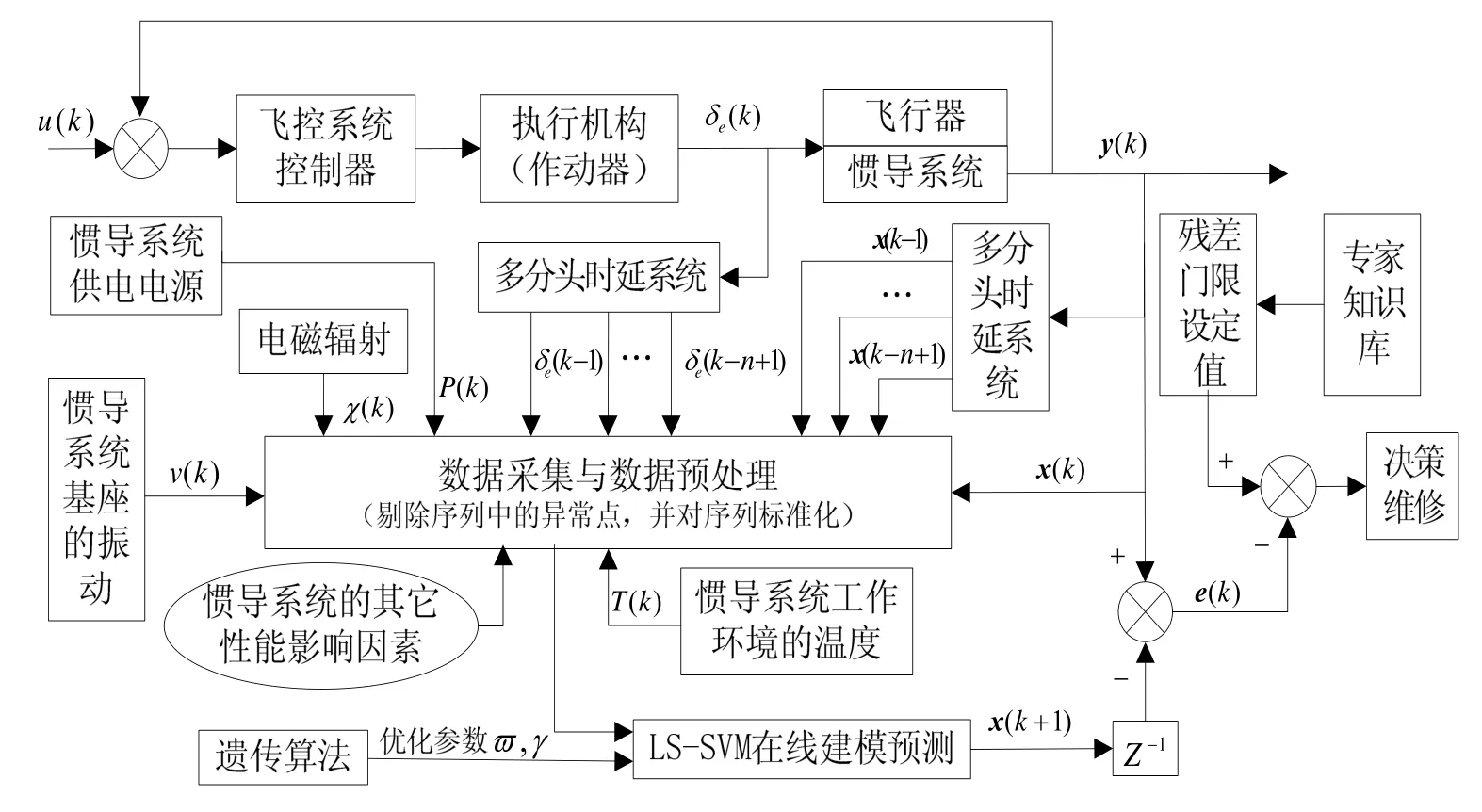
图1 惯性导航系统的故障在线检测模型Fig.1 Fault online test model of inertial navigation system

由于式(7)所示的惯导系统故障预测模型涉及较多参数，预测速度难以提高，所以采用两步法来提高惯导系统的故障预测速度。

步骤一：采用简化后的式(9)对x(t)第i个分量在k+1时刻的值进行预测。

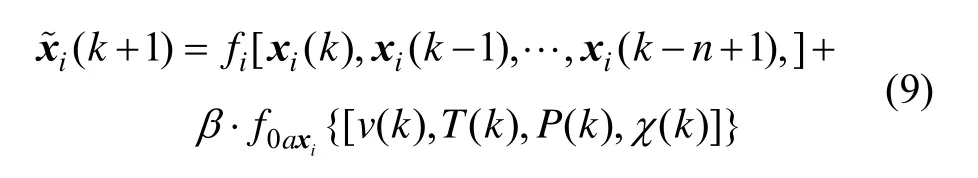
式(9)所示的预测模型，可以通过对LS-SVM回归算法的改进，来提高算法的鲁棒性和速度，下面对其算法进行研究。

2 LS-SVM算法的改进

2.1 LS-SVM算法

对于给定的训练样本集：

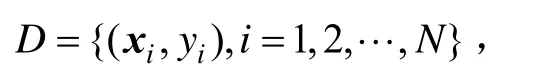
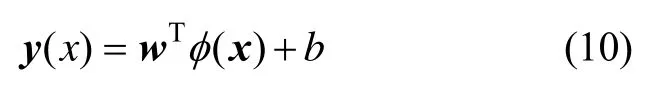
根据结构风险最小化原理，把回归问题表示为下列约束优化问题：

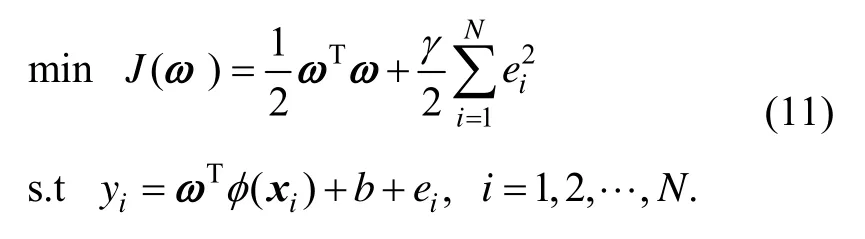
式中，γ为正则化参数，b为常值偏差。通过其对偶形式，采用Lagrange乘子法求解得：

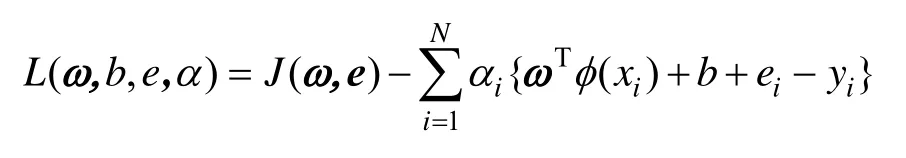
式中，iα为拉格朗日乘子，根据KKT(Karush-Kuhn-Tucker)条件对式(12)的分别求偏导并令其等于0，从中消去ω、ei，整理可得矩阵方程：

2.2 在线LS-SVM算法的改进

在线LS-SVM回归的时间序列学习，可以认为是一个随时间滚动的优化过程[14-15]，针对引言部分提到此方法的两个不足，对其前期的数据预处理和后期的在线递推回归做了一些方法上的改进。

2.2.1 数据预处理

因为任何确定的物理量在极短时间内不可能发生过程的突变，所以假设经历数秒后，惯性测量组件已经转入稳态工作，对于测量组件在k时刻采集的故障检测样本序列X′(k)，设1in≤ ≤，对于第i行元素，按照进入样本窗的先后顺序，取其最后进入的连续 4个元素，实时计算这四点的标准差，然后再按式(16)作3次差分，计算出.

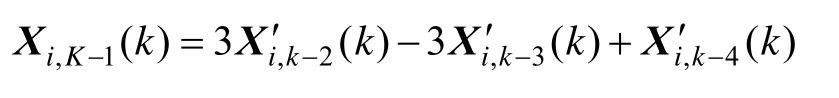
2.2.2 在线LS-SVM回归算法的改进

假设学习的样本X′(k)经过数据预处理后变为，因为样本窗在加入新样本，剔除旧样本的过程是实时滚动更新的，所以在线LS-SVM核函数矩阵Ω、待求的 Lagrange乘子α及常值偏差b都应该是k的函数。即在k时刻，它们可分别表示为：

则最小二乘支持向量机的输出式(15)变为：

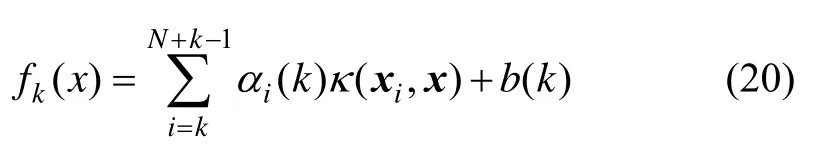
式(13)也可以改写为：

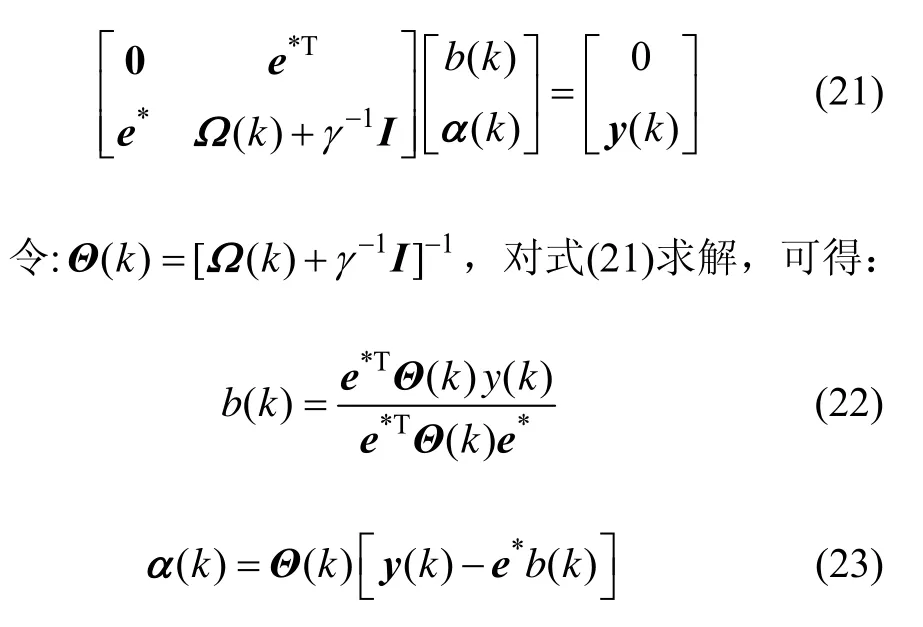
从式(22)(23)可以看出，只要求出Θ(k)，便可以得到b(k)、α(k)的解，对Θ(k)的计算过程如下：

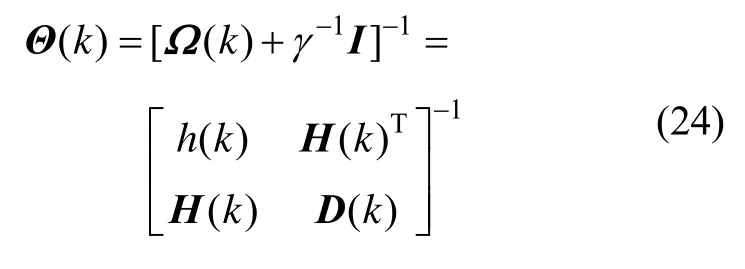
式(24)中，各参数计算公式如式(25)～(27)所示：

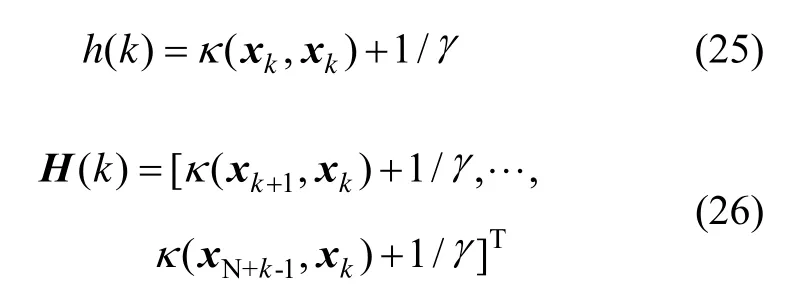
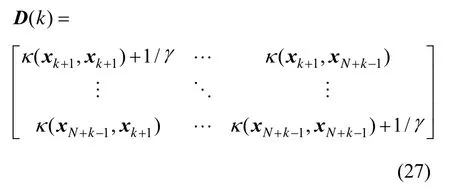
上述式(19)～(27)是通常所用的求解方法，但因为该方法每次得到的都是一个时变的线性方程组，所以每次训练，求解的计算量都较大，尤其是当样本数目较多时，会严重影响在线预测的速度。为了减少在线LS-SVM回归算法的计算量，下面的分析通过对Θ(k)及Θ(k+1)求解过程的分析，建立了一种Θ(k)的递推求解方法[16]。

对式(24)求解可得：

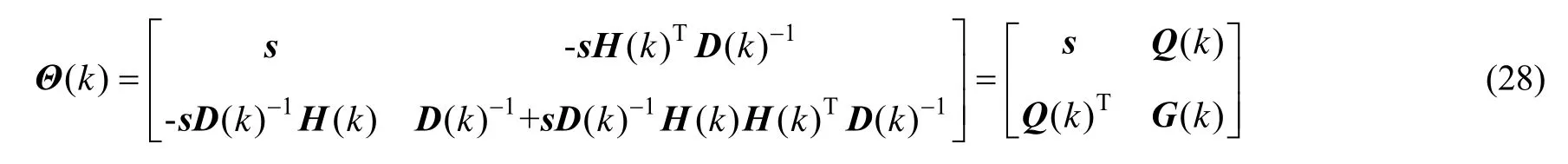
式(28)中，s表达式如下式(29)所示：

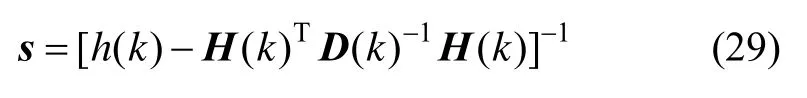
观察式(29)，可以求得：

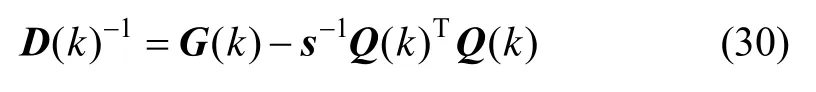
在第k+1时刻，新样本加进来取代了旧样本，此时，核函数矩阵变为：

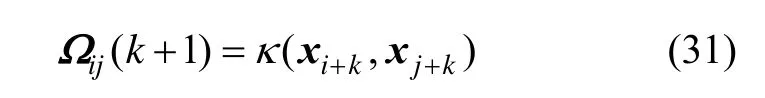
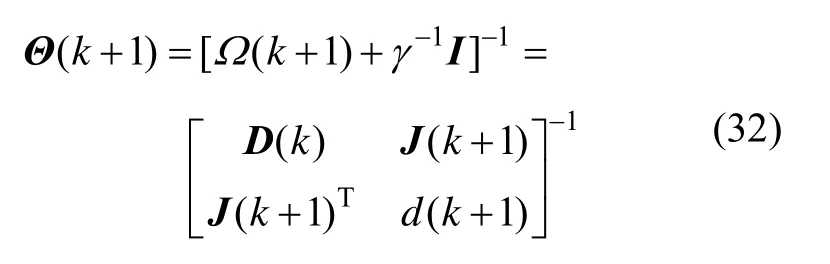
式(32)中，各参数计算公式如(33)(34)所示：

对式(32)求解得：

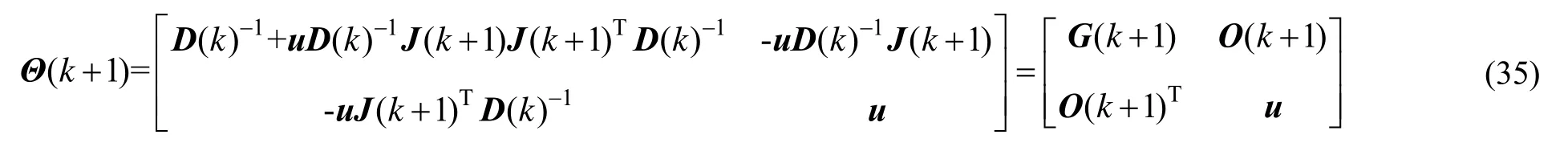
式(35)中，u的表达式如下式(36)所示：

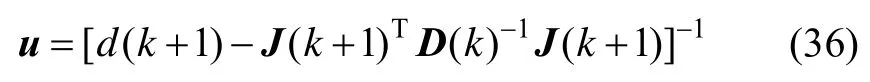
从式(20)～(34)可以看出，在样本窗在加入新样本，剔除旧样本时，假设初始Θ(0)是直由接求逆得到的，然后对Θ(0)按式(28)进行分块后，按式(30)求得，再将代入式(35)便可求得Θ(1)，重复上述递推过程就可以求得其余Θ(k)及Θ(k+1)，这种递推求解法明显的能减少计算量。

3 惯性测量组件故障在线检测的实现

建模时选用径向基核函数来提高故障状态原始信息最优的特征抽取性能及非线性预测能力。关于核函数及其参数的选取和优化方法，文献[17]已经做了详细介绍，所以不再重复。

对于式(9)所建立的惯性测量组件故障在线预测模型，其实现步骤如下：

1）设定时刻K=0；

2）惯性测量组件每采集一次样本，K自动加1；

3）判断惯导系统工作的环境因素是否超限，若超限，置β=1，否则置β=0；

4） 对观测样本序列数据按 2.2.1节所述的数据预处理方法进行处理；

5）判断K是否大于N-1，是则进行以下第（6）步，否则返回第2）步继续；

6）按式(9)建立的模型进行故障在线预测；

7） 按 2.2.2 节所述内容，计算Ω(k)，Θ(k)，α(k)及b，并预测；

8）把预测得到的残差和设定的门限值比较并输出故障诊断结果。

故障检测模型的逼近能力，可以采用均方根误差(RMSE)进行评价。

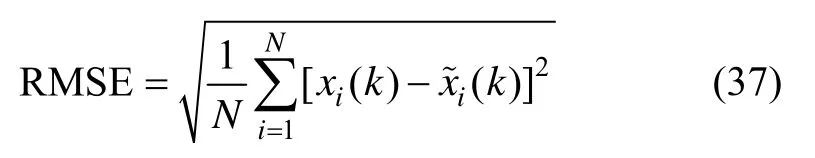
4 仿真实验与结果分析

仿真实验时，设定预测模型的输入输出延时为5 s，利用交叉验证法选定γ=30，径向基核函数的宽度优化后取为3，纵向飞行控制律为：

4.1 惯性测量组件故障检测性能的比较

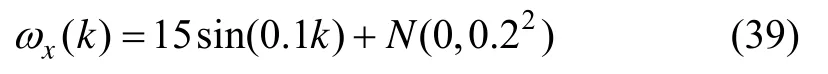
把所述方法和标准SVM、改进前的LS-SVM及自行设计的一个 10-10-5-1四层（输入层、预处理层、隐含层、输出层）神经网络模型（标准SVM、LS-SVM与文中所使用的核函数参数及正则化参数完全相同）对原始信号135个样本点的检测结果做了比较，从表1可以看出，本文改进之后的在线LS-SVM方法在预测精度和预测时间上具有明显的优势。

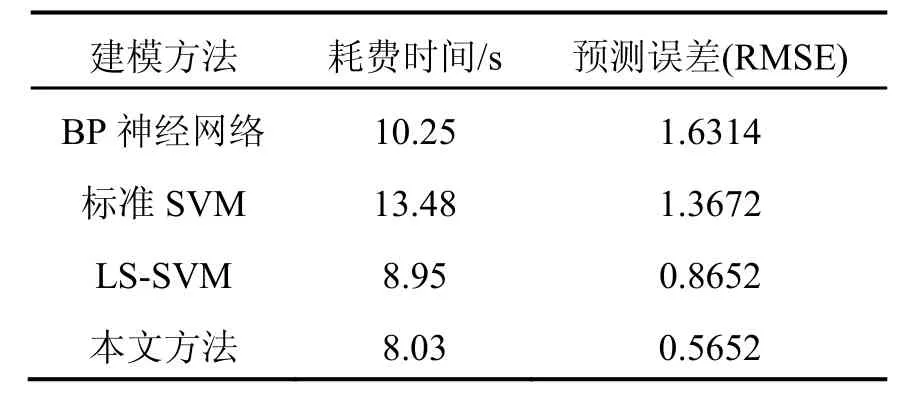
表1 预测性能参数对比Tab.1 Comparison of prediction performance

4.2 惯性测量组件故障检测结果的分析

1）卡滞故障

假设俯仰角惯性测量陀螺在时刻点k=80时，出现了卡滞故障，其输出情况如图2所示，由图可知，卡滞故障发生时刻，陀螺的实际输出信号出现了跳变，之后近似常值信号输出。这是因为本文所用的预测模型采用的是动态数据窗在线实时建模的思想，加大了对数据预处理的力度，当卡滞故障发生后，它对突变的原始样本点数据具有较强的鲁棒性，所以在卡滞故障发生时刻，预测曲线没有迅速逼近陀螺的实际输出信号，而是一个缓慢变化的过程。同时还可以从预测的残差曲线明显的看出，其它时刻点的残差变化不及卡滞故障发生时刻明显。

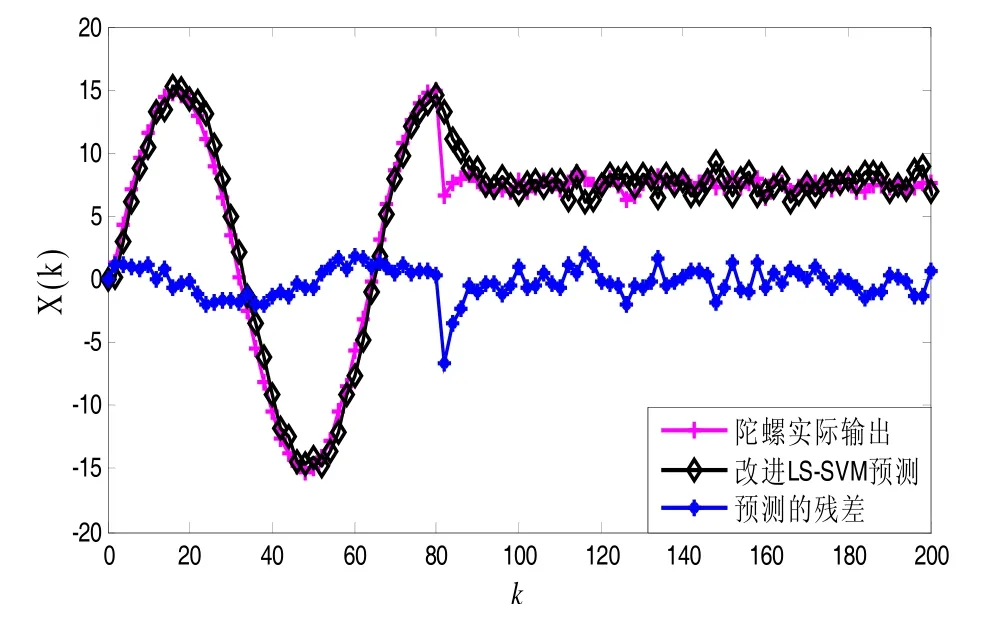
图2 卡滞故障预测及其残差曲线Fig.2 Prediction curves of lock fault and residual error

2）恒偏差故障

假设俯仰角测量陀螺在时刻点k=80时，出现了恒偏差故障，其输出情况如图3所示。

由图3可知，在时刻点k=80之后，陀螺的输出信号曲线及预测曲线整体沿Y轴向上或向下近似平移偏差绝对值个单位，方向由其偏差的符号决定。由于本文预测方法能够在很短的时间内通过调整，适应新的预测系统的结构参数，并进行预测输出，所以残差变化会在故障点出现明显的一个跳变。故障发生前后，其残差变化并不明显。

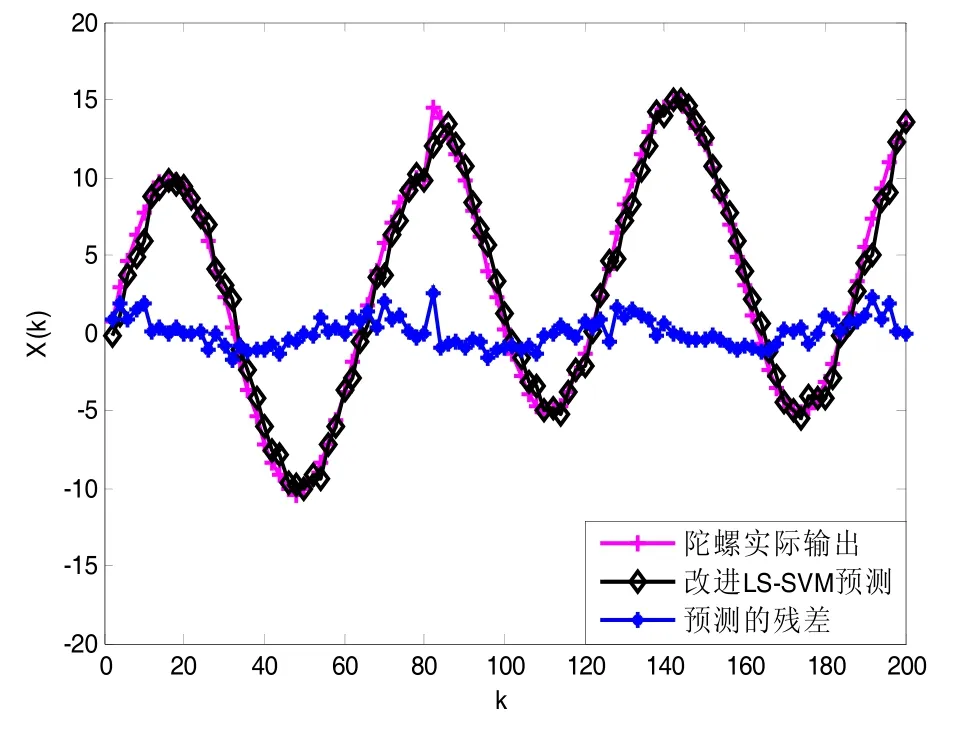
图3 恒偏差故障预测及其残差Fig.3 Prediction curves of constant bias fault and residual error

5 结 论

为提高惯性测量组件工作的可靠性和导航性能，对其故障模式进行了分析，接着对在线LS-SVM回归算法进行了改进，随后应用改进的算法对惯性测量组件状态观测样本数据的异常点进行了修正并建立了故障检测模型。仿真实验表明本文方法对包含异常点的样本预测，具有较强的鲁棒性和较快的预测速度。

在载机强机动条件下，采用什么方法对其惯性测量组件进行故障在线预测与诊断，如何将收集的惯导系统各故障信息准确对应到它的各个状态点，构建基于性能的惯导组件故障预测与健康管理体系方法，仍需要做更深的研究。

（References）：

[1]唐圣金，郭晓松，王振业，等.基于故障树的多光纤陀螺冗余系统可靠性分析[J].中国惯性技术学报，2013，21(2)：259-264.TANG Sheng-jin，GUO Xiao-song，WANG Zhen-ye，et al.Reliability analysis for redundant system with multiple FOGs based on fault tree analysis method[J].Journal of Chinese Inertial Technology，2013，21(2):259-264.

[2]Friedman M，Schwartz J.Techniques for architecting high performance hybrid test systems [C]//IEEE，Autotestcon.Salt Lake City，UT，2008:282-285.

[3]Yang B S，Han T，An J L.Neural network for fault diagnosis of rotating machinery[J].Mechanical Systems and Signal Processing，2004，18(3):645-647.

[4]钮永胜，赵新民.基于神经网络在线建模的非线性动态系统中传感器故障检测方法[J].宇航学报，1998，19(1)：55-59.NIU Yong-sheng，ZHAO Xin-min.Multiple sensor failure detection in nonlinear system based on system identification method using on-line learning neural network[J].Journal of Astronautics，1998，19(1):55-59.

[5]Keerthi S S，Lin C J.Asymptotic behaviors of support vector machines with Gaussian kernel[J].Neural Computation，2003，15(7):1667-1689.

[6]Chapelle O，Vapnik V，Bousquet O.et al.Choosing multiple parameters for support vector machines[J].Machine Learning，2002，46(1-3):131-159.

[7]张浩然，汪晓东.回归最小二乘支持向量机的增量和在线式学习算法[J].计算机学报，2006，29(3)：400-406.ZHANG Hao-ran，WANG Xiao-dong.Incremental and online learning algorithm for regression least squares support vector machine[J].Chinese Journal of Computers，2006，29(6):400-406.

[8]叶美盈，汪晓东，张浩然.基于在线最小二乘支持向量机回归的混沌时间序列预测[J].物理学报，2005，54(6)：2569-2573.YE Mei-ying，WANG Xiao-dong，ZhANG Hao-ran.Chaotic time series forecasting using online least squares support vector machine regression[J].Acta Physica Sinica，2005，54(6):2569-2573.

[9]胡良谋，曹克强，苏新兵，等.基于LS-SVM的飞控系统传感器故障诊断[J].飞行力学，2011，29(3)：36-39.HU Liang-mou，CAO Ke-qiang，SU Xin-bing，et al.Fault diagnosis for flight control system’s sensor based on LSSVM [J].Flight Dynamics，2011，29(3):36-39.

[10]段江涛，陈怀民，王亮.基于检测滤波器的俯仰角速率传感器故障检测研究[J].计算机测量与控制，2011，19 (4)：785-788.DUAN Jiang-tao，CHEN Huai-min，WANG Liang.Pitch angle sensor fault detection based on detection filter[J].Computer Measurement &Control，2011，19(4):785-788.

[11]WU Xue-zhong，XIE Li-qiang，XING Jian-chun，et al.A z-axis quartz tuning fork micro machined gyroscope based on shear stress detection[J].IEEE Sensors Journal，2012，12(5):1246-1252.

[12]Ma J，Theiler J，Perkins S.Accurate on-line support vector regression[J].Neural Computation，2003，15(11):2683-2703.

[13]Özbayoğlu G，Evren Özbayoğlu M.A new approach for the prediction of ash fusion temperatures:A case study using Turkish lignites[J].Fuel，2006，85(4):545-552.

[14]Tay F E H，Cao L J.Application of support vector machines in financial time series forecasting[J].Omega，2001，29(4):309-317.

[15]Suykens J A K，Vandewale J.Least squares support vector machine classifiers[J].Neural Processing Letters，1999，9(3):293-300.

[16]吴琼，杨以涵，刘文颖.基于最小二乘支持向量机的电力系统暂态稳定在线预测[J].中国电机工程学报，2007，27(25)：38-43.WU Qiong，YANG Yi-han，LIU Wen-ying.Electric power system transient stability on-line prediction based on least squares support vector machine[J].Proceedings of the CSEE，2007，27(25):38-43.

[17]王强，田学民.基于改进的GA-LSSVM的软测量建模方法[J].北京理工大学学报，2012，32(10)：1031-1035.WANG Qiang，TIAN Xue-min.Soft Sensing Based on Improved GA-LSSVM [J].Journal of Beijing Institute of Technology，2012，32(10):1031-1032.

Fault online test method of inertial measurement units based on improved LS-SVM

YANG Hui ，ZHAO Yan ，TENG Chong ，LI Min
(School of Instrumentation and Opto-electronic Engineering，Beihang University，Beijing 100191，China)

In order to improve the reliability and navigation performance of the inertial navigation system，the fault mode and test model were analyzed.Two ameliorations were made for the method of the online least squares support vector machine(LS-SVM):1) The singularity was found out and disposed with Newton interpolation method among the sample data which was shifted and updated in the observation window.2) A recursive solution method was put forward based on the process regression analysis of online LS-SVM，and the inertial measurement units outputs complement with elevator angle variation and environmental factors were chosen as the observed sample sequence.Then the proposed method was used to improve the accuracy and timeliness of the online test model for the inertial navigation system.Finally，the simulation was made when the inertial navigation system has no fault and has lock fault or constant bias fault.The results show that，compared with SVM，LS-SVM，and BP neural network modeling，the proposed method has higher learning speed and robustness performance.

inertial measurement units;online least squares support vector machine;dynamic data window;robustness;fault prediction

U666.1

A

1005-6734(2014)03-0409-07

10.13695/j.cnki.12-1222/o3.2014.03.025

2013-11-20；

2014-03-12

航空科学基金资助项目(20110112007，20100818018)

杨辉（1983—），男，博士研究生，从事导航制导与控制的研究。E-mail：happyncu@163.com

联 系 人：赵剡（1956—），男，教授，博士生导师。E-mail：zhaoyan@buaa.edu.cn