一种惯性辅助卫星完好性监测多解分离法的优化方法

雷宝权，曾 进

（中航工业西安飞行自动控制研究所，西安 710065）

一种惯性辅助卫星完好性监测多解分离法的优化方法

雷宝权，曾 进

（中航工业西安飞行自动控制研究所，西安 710065）

针对惯性辅助卫星完好性监测多解分离法计算量大的问题，给出了一种基于参数序贯复用的优化方法。在对多解分离法及其计算量分析基础上，采用序贯处理技术，推导了低阶顺序处理多解分离法。同时根据系统结构特点以及滤波器间量测信息高度相关性，提出滤波器参数复用方法，避免参数重复计算。通过仿真实验，从故障引入时间和可见星数目变化两个方面对优化前后多解分离法的计算量进行了对比。仿真结果表明该优化方法可以有效降低多解分离法的计算量，便于工程应用。

卫星导航；惯性导航；卫星完好性监测；故障检测隔离；多解分离法；序贯处理；参数复用

全球导航卫星系统(GNSS)的广泛应用，使得实时卫星信号完好性监测越发的重要，受限于卫星星座分布和卫星伪距量测精度，接收机自主完好性监测(RAIM)无法提供足够的可用性满足飞机的导航目标，因此，依靠于 GNSS互补性强的惯导(inertial)辅助GNSS完好性监测就得到了人们的重视[1-3，8]。惯性辅助卫星完好性监测技术根据检验统计量特征的不同可分为两类：一是位置域内的多解分离法(MSS)[2-6]；二是距离域内的自主完好性监测外推法(AIME)[1-3，7-10]。目前应用最为广泛的是MSS法。

MSS法最早由 Brenner[1]提出使用多个GPS/inertial卡尔曼滤波器进行卫星故障检测而来；Kevin[4]等人在主-子滤波器的基础上，扩展了子-子滤波器集，用以识别、隔离检测到的故障星；Honeywell公司的Curt等人[5]提供了基于 MSS法的卫星完整性监测技术半物理仿真实现和飞行测试的结果；Lee等人[1]则分析比较了MSS法和AIME法的优缺点，指出MSS法需要设计多个滤波器，计算量大。从这些公开发表的文献资料来看，当可见星数为 10颗时，基于MSS法的故障检测隔离(FDE)算法需要56个滤波器的存储空间，开环并行计算，这对导航计算机的计算量和存储量要求都很高，不利于MSS法的工程应用，如何降低MSS法的计算量，有待进一步研究。

本文首先给出基于多解分离的 FDE算法基本原理，然后针对其故障检测(FD)时的计算特点，分析了FD整个处理流程的计算量，提出了一种降低MSS法FD计算量的滤波器参数序贯复用优化方法(同理MSS法FE)，并将该方法计算量与优化前MSS法计算量进行了仿真对比，验证了其有效性。

1 基于多解分离的FDE算法

1.1 基于多解分离的FDE算法基本原理

MSS法是一种将“RAIM”概念扩展到 GNSS/inertial组合导航系统的有效方法。它的FD由1个处理N颗可见星数据的主滤波器、N个使用去除一颗可见星的其余所有卫星量测的子滤波器组成，子滤波器的量测隔离了可见星n。FE则需要进一步构造个子-子滤波器。MSS法 FD滤波器层次结构如图1所示。各滤波器的解为：主滤波器解，子滤波器解，子-子滤波器解。通过与的位置估计状态相减，得到解分离估计，然后与检测门限比较，即可进行故障检测。故障星的隔离需要进一步比较，处理过程与故障检测类似。

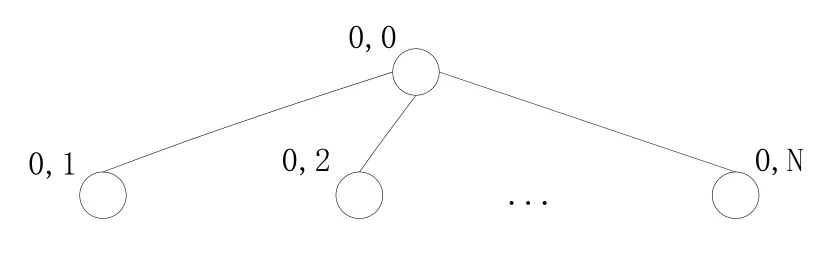
图1 MSS法故障检测滤波器层次结构图Fig.1 MSS method FD filter hierarch

1.2 MSS法GNSS/inertial组合卡尔曼滤波器模型

MSS法的GNSS/inertial系统采用伪距、伪距率组合，亦可仅采用伪距。系统的状态量包括INS误差状态量和GNSS误差状态量。

选取东-北-天(ENU)地理坐标系为导航参考坐标系，INS误差状态量包括导航系下的平台姿态误差、速度误差、位置误差δLδλδh和机体系下的惯性器件误差以及高度计偏差δhb；GNSS误差状态变量则包括各颗可见星的不相关的伪距偏差和由钟差引起的距离误差δtu，其中N为可见星数。系统误差状态量可表示为：

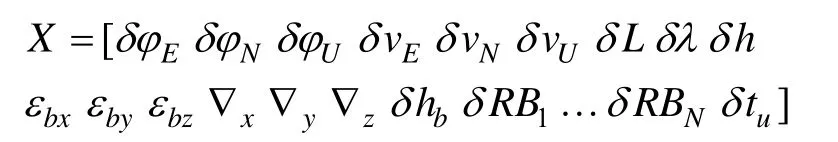
系统的状态方程：

伪距偏差δRB和高度计偏差δhb均设定为一阶马尔柯夫过程，系统噪声：；当可见星数N取为6时，状态转移矩阵为：

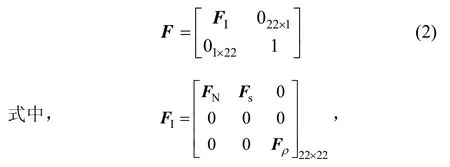
其中，FN的非零元素可由简化的INS导航算法误差模型推导而来，

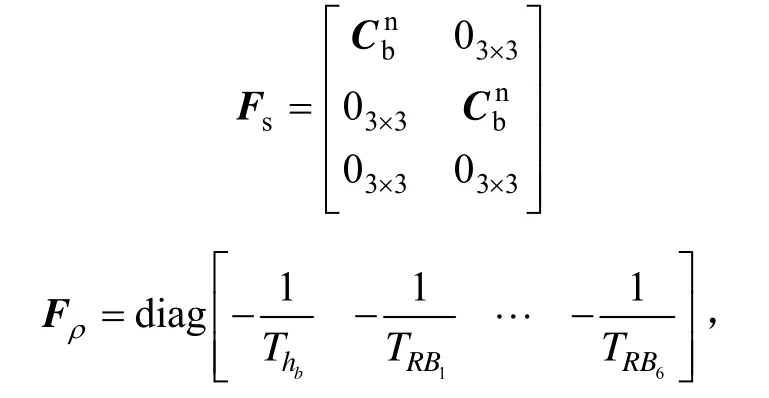
由每颗可见星n的测量伪距和计算伪距之差组成Δz，系统观测方程为：

为卫星接收机给出的测量伪距，为计算伪距，由INS位置信息与接收机解码的卫星导航电文中卫星n位置坐标计算得出；

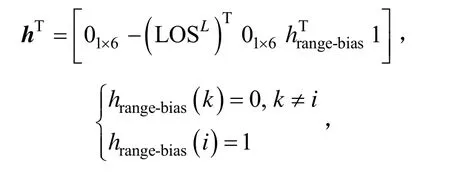
v为量测噪声，包含接收机随机误差和电离层、对流层、多径等误差。

1.3 故障检测

对于子滤波器n来说，主滤波器与子滤波器的解分离矢量为：

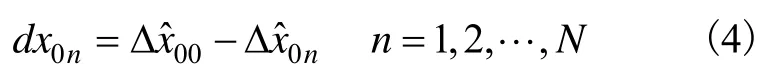
则水平位置检验统计量d0n为：

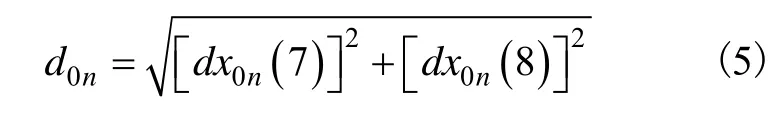
式中，7和8表示纬度和经度误差状态。子滤波器综合N-1个量测量的不同组合，得到各自的检验统计量和对应协方差矩阵dP0n，dP0n描述了主滤波器和子滤波器距离的统计量：

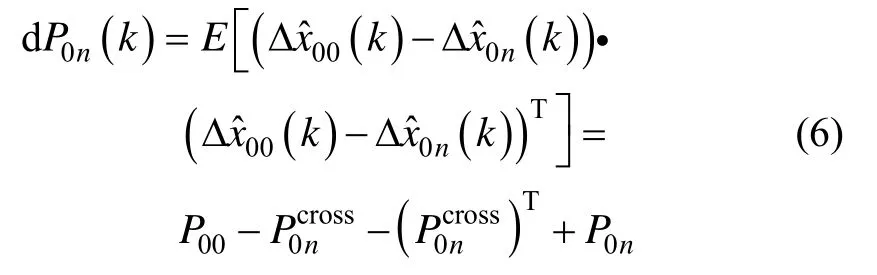
当没有卫星故障时，量测噪声的存在可能带来误警，因此，检测门限需由最大可允许的误警率决定，通过公式(7)计算：

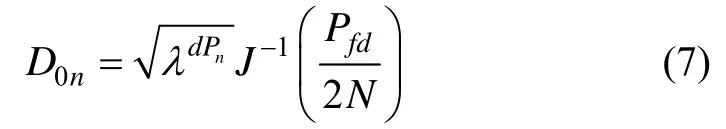
依据N组检验统计量和检测门限，MSS法故障检测判据为：当所有检验统计量均小于检测门限时，系统无故障；当至少出现一个检验统计量大于其检测门限时，系统存在故障。

1.4 故障隔离

2 MSS法FD计算量分析

MSS法FD处理流程如图2所示。

分析MSS法FD处理流程的计算特点，基于MSS法的FD算法基础是卡尔曼滤波，其主滤波器的解和协方差传播为：

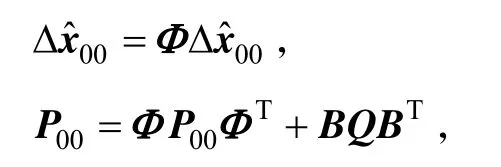
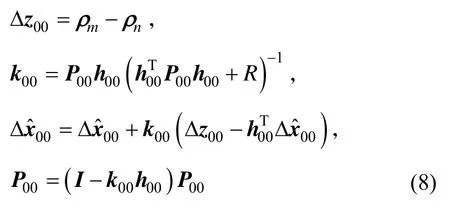
式中，Φ为状态转移阵，由F阵离散化而来；B为噪声分布阵；为量测噪声协方差阵。单独分析上述传播方程，可得MSS法中主滤波器每一步滤波的计算情况：

表1 MSS法中主滤波器每一步滤波计算情况Tab.1 Computing details of main filter in MSS method

经过Matlab计算分析：矩阵加法、减法和转置计算量相当，乘法计算量大约为加法的10倍，矩阵求逆计算量大约为加法的100倍，忽略主滤波器中矩阵数据的差异性影响，定义主滤波器中一次矩阵加法计算量为1个单位时间(1tU)，则MSS法中主滤波器每一步滤波的总计算量为238tU，其中求取卡尔曼增益阵k00和协方差阵P00的计算量为206tU，占总计算量的87%。

进一步分析 MSS法中子滤波器每一步滤波的计算量，子滤波器与主滤波器的差异为：1)量测少一维可见星信息；2)每一步需多计算交叉协方差阵。从MSS法FD计算流程可知主、子滤波器开环并行计算，忽略矩阵维数差异，则单个子滤波器将比主滤波器多出109tU的计算量，当可见星数N取为6时，MSS法中滤波器每一步滤波的计算情况为：

表2 MSS滤波器每一步计算情况Tab.2 Computing details of filters in MSS method

则MSS法滤波器每一步滤波总计算量约为2320tU。检测部分各子滤波器的检验统计量d0n、检测门限D0n和水平保护门限HPL的计算量固定，不作考虑。

如果继续考虑故障隔离的子-子滤波器解Δxˆnm，MSS法的计算量和存储量都将远远增大，极大的限制了MSS法在工程上的使用，因此必须对MSS法计算处理流程进行优化。

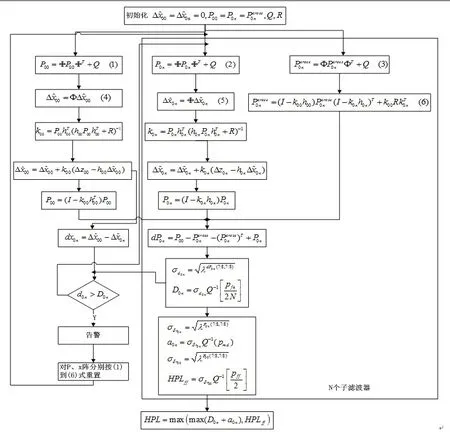
图2 MSS法故障检测处理流程图Fig.2 MSS method FD process flow chart

3 MSS法FD计算量优化方法

根据MSS法FD部分的计算量分析，可以发现：

① MSS法FD中每一步滤波的计算量最大来源为求取卡尔曼增益和协方差阵，约占总计算量的90%以上；

② 主滤波器和去除一颗可见星的子滤波器量测信息相关度高，但两者却实行开环并行计算，当可见星为6颗时，每一步计算需同时开辟7个卡尔曼滤波器存储与计算空间，造成了重复计算。

3.1 序贯处理

对于问题①中求取卡尔曼增益阵和协方差阵计算大，采用卡尔曼滤波的序贯处理技术。它是将量测更新中对z的集中处理分散为对z各分量组的顺序处理，使对高阶矩阵的求逆转变为对低阶矩阵的求逆。

设主滤波器的离散状态方程和量测方程为：

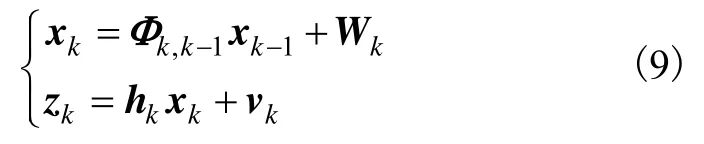
式中，Wk和vk均为独立零均值白噪声序列，协方差阵分别为Qk和Rk，Rk为分块对角阵，当可见星为6颗时，可将Rk改写为：

表3 常规和采用序贯处理技术MSS法计算量对比Tab.3 Calculation comparison between normal MSS method and MSS method with sequential processing

可以看到，随着矩阵阶数的降低，采用低阶顺序处理的总计算量也随之下降。

3.2 滤波器参数复用

对于问题②，MSS法FD中子滤波器量测相较主滤波器只去掉了1颗可见星，则两者滤波器信息具有强的相关性，采用滤波器参数复用的方法优化，利用主滤波器参数得到子滤波器参数，避免参数重复计算，从而降低计算量。

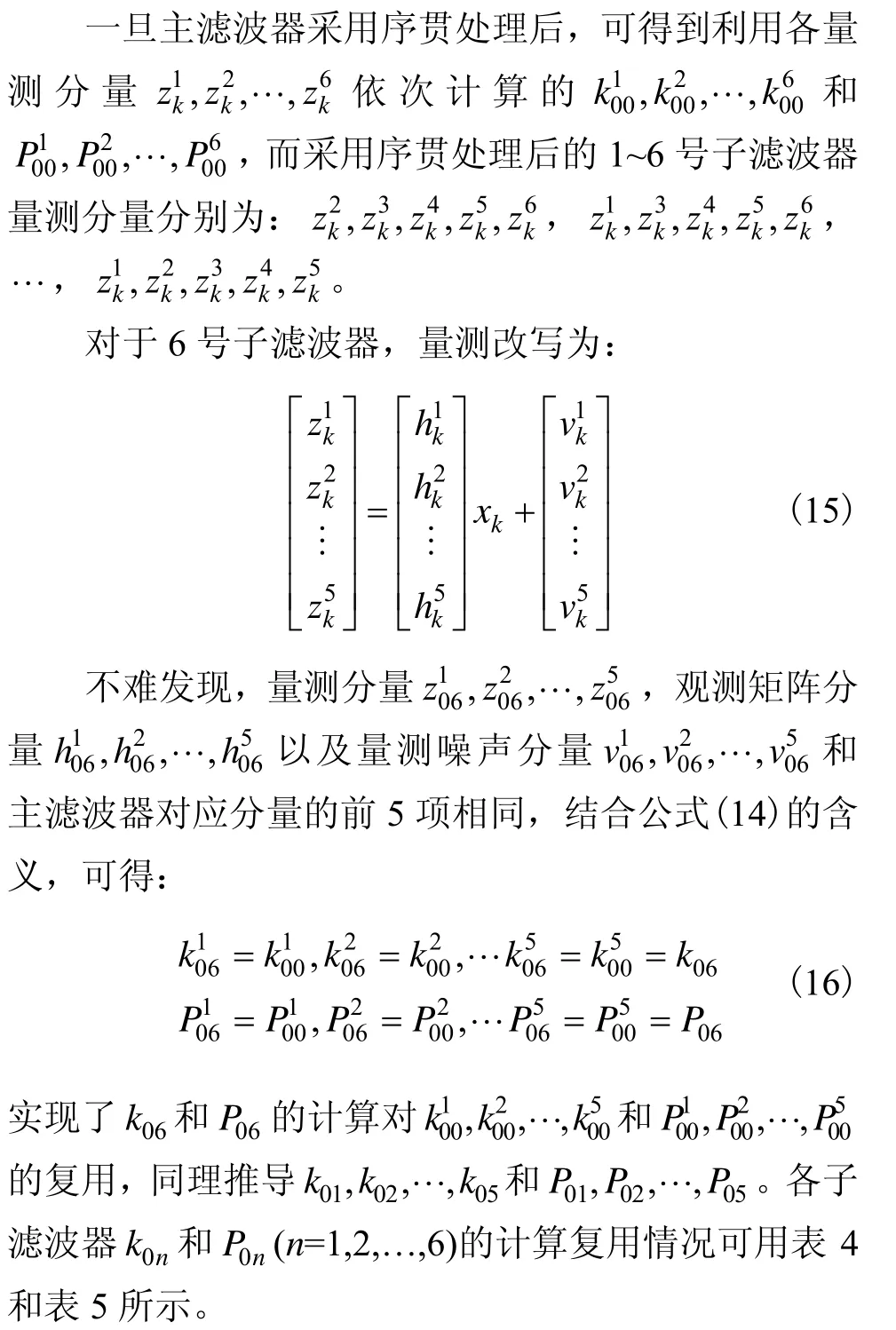
从表中可看到，子滤波器组k0n和P0n(n=1，2，…，6)复用了约 41.6%的主滤波器计算值，可以很明显的降低k0n和P0n的计算量，节省计算时间。

在MSS法FD中采用滤波器参数复用方法后，总计算量将进一步降低。各方法滤波器计算量对比如表6所示。

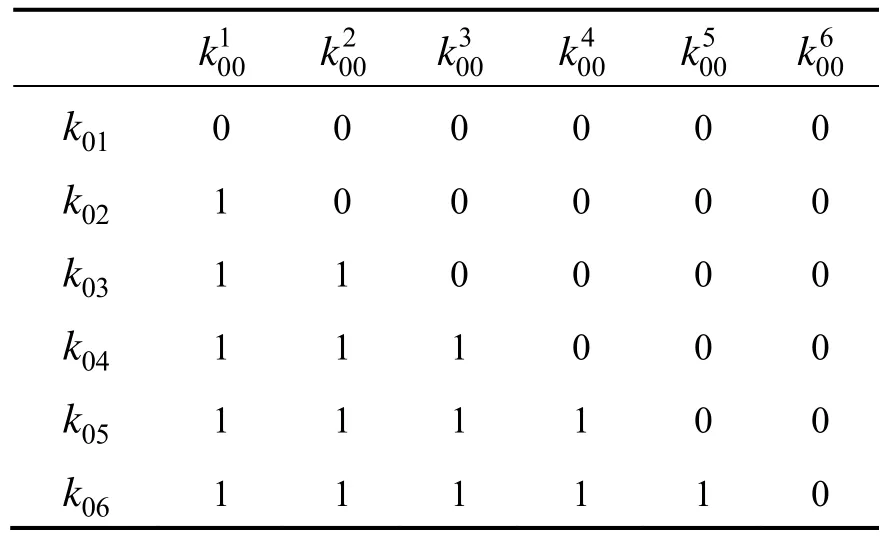
表4 k0n复用情况表（0表示：无复用情况；1表示：复用）Tab.4 Parameters reuse details of k0n（0 :no reuse ;1 :reuse）

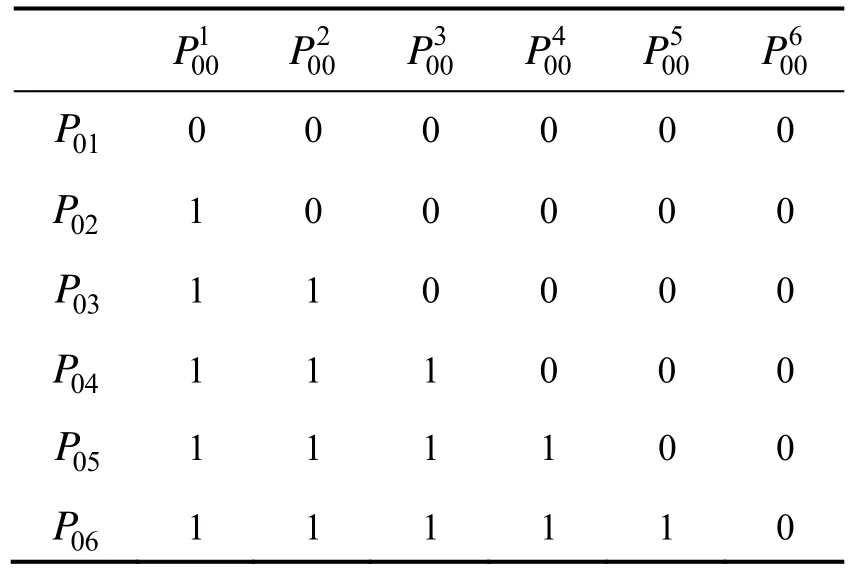
表5 P0n复用情况表（0表示：无复用情况；1表示：复用）Tab.5 Parameters reuse details of P0n（0 :no reuse ;1 :reuse）

表6 各方法滤波器计算量对比Tab.6 Calculation comparisons of three methods

4 仿真结果及分析

本文对MSS法、采用序贯处理技术MSS法和采用参数序贯复用优化 MSS法的计算量分别进行Matlab环境下的仿真。由飞行轨迹发生器产生轨迹数据；卫星星历数据采用模拟仿真数据，采样率1 Hz，量测噪声为10 m(接收机误差、电离层误差、对流层误差和多径等)，卫星伪距偏差为 2 m(卫星时钟稳定性误差和星历预测误差等)；INS模拟器产生惯性数据，采样率50 Hz，惯性器件误差如表7所示；试验中各卫星伪距由卫星星历位置和轨迹位置之间的几何距离加上伪距误差仿真产生。仿真时间800 s。

表7 惯性器件误差Tab.7 Inertial components errors

为了评估优化方法降低MSS法计算量的有效性，引入Matlab的tic和toc指令记录比较MSS法、采用序贯处理MSS法和采用参数序贯复用优化MSS法故障检测滤波解算的计算时间，两两比较，差值越大，则说明优化方法成效越好。

仿真条件设定为：第300 s时，在第2颗可见星伪距上加上100 m阶跃故障，MSS法检测出故障时，记录的故障检测每一步滤波解算平均运行时间(计算量)tnormal=0.002358 s(Matlab执行时间)。

同样条件下得到采用序贯处理的 MSS法故障检测每一步滤波解算平均运行时间txg=0.002 023 s；采用参数序贯复用优化方法的 MSS法故障检测每一步滤波解算平均运行时间txgfy=0.001 629 s。

对于不同时刻给第2颗可见星引入故障后，MSS法和采用参数序贯复用优化方法的 MSS法故障检测每一步滤波解算平均运行时间对比如表8所示。

表8 不同故障引入时间MSS法和优化后的MSS法滤波计算量对比Tab.8 Normal MSS and improved MSS calculation comparison for different fault involvement moments

进一步考虑可见星数对优化方法的影响，整个飞行过程中的可见星数如图3所示，当可见星数变化时(量测向量维数变化)，分别在MSS法和采用参数序贯复用优化方法的 MSS法故障检测中每一步滤波解算平均运行时间对比如表9所示。

从表8、表9可以看出：

① 采用优化方法的MSS法滤波计算量明显小于常规MSS法，有效地降低了MSS法的计算量，且优化效果与故障引入时间没有关系；

② 随着可见星数的增加，参数序贯复用优化方法对MSS法的优化效果越好。

表9 可见星数变化时常规MSS法和优化后的MSS法滤波计算量对比Tab.9 Calculation comparison between normal MSS and improved MSS as visible satellite numbers changing

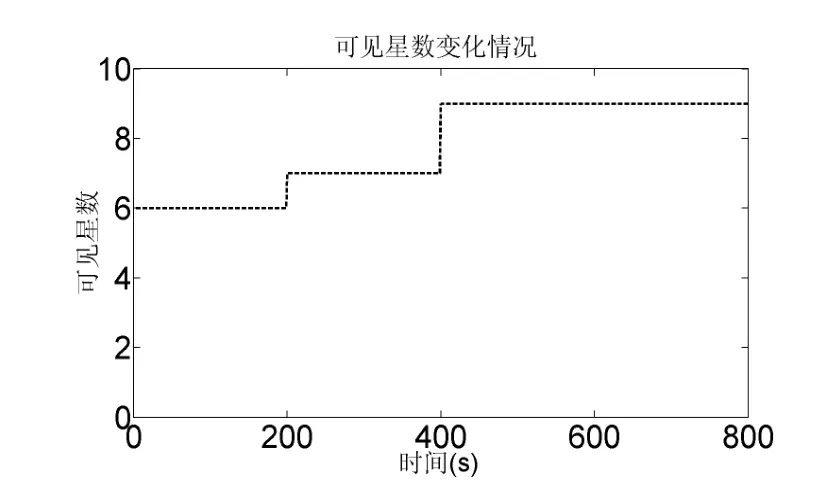
图3 可见星数Fig.3 Numbers of visible satellites

5 结 论

针对惯性辅助卫星完好性监测多解分离法计算量大、不利于工程实现的问题，提出了一种基于序贯处理和滤波器参数复用的优化MSS法，并与优化前的MSS法就故障检测部分的计算量进行了理论分析与仿真实验(同理分析故障隔离部分)。仿真结果表明：相比于常规MSS法，采用参数序贯复用优化方法，可以有效地降低MSS法整个计算处理流程的计算量。因此，本文提出的基于参数序贯复用优化的MSS法为后续进一步的工程化应用研究奠定了基础。

（References）：

[1]Bhatti U I.Improved integrity algorithms for integrated GPS/INS systems in the presence of slowly growing errors[D].London:Center for Transport Studies Department of Civil and Environmental Engineering Imperial College，2007.

[2]李晓东，赵修斌，庞春雷，等.PBN概念下的GNSS/SINS组合导航完好性算法[J].电光与控制，2013，20(1)：44-48.LI Xiao-dong，ZHAO Xiu-bin，PANG Chun-lei，et al.Integrity Monitoring of Integrated GNSS/SINS System Based on PBN[J].Electronics Optics &Control，2013，20(1):44-48.

[3]冀捐灶，彭兴钊，杜军，等.三种卫星故障检测策略的对比研究与仿真[J].计算机仿真，2013，30(9)：51-55.JI Juan-zao，PENG Xing-zhao，DU Jun，et al.Comparison and Simulation of Three Satellites’ Failure Detection Methods[J].Computer Simulation，2013，30(9):51-55.

[4]Vanderwerf K.FDE using multiple integrated GPS/inertial kalman filters in the presence of temporally and spatially correlated ionospheric errors[C]//Proceedings of ION-GPS-2001，14th International Technical Meeting of the Satellite Division of the Institute of Navigation.Salt Lake City，UT，2001:2676-2685.

[5]Curt C，Mike I，Jim M，et al.Performance of Honeywell’s Inertial/GPS Hybrid(HIGH)for RNP operations[C]//Proceedings of IEEE/ION PLANS.San Diego，USA，2006:244-255.

[6]刘海颖，岳亚洲，杨毅钧，等.基于多解分离的GNSS/Inertial组合系统完整性监测[J].中国惯性技术学报，2012，20(1)：63-68.LIU Hai-ying，YUE Ya-zhou，YANG Yi-jun，et al.Integrity monitoring for GNSS/Inertial based on multiple solution separation[J].Journal of Chinese Inertial Technology，2012，20(1):63-68.

[7]刘海颖，冯成涛，王惠南.一种惯性辅助卫星导航及其完好性监测方法[J].宇航学报，2011，32(4)：775-780.LIU Hai-ying，FENG Cheng-tao，WANG Hui-nan.A method of inertial aided satellite navigation and integrity monitoring[J].Journal of Astronautics，2011，32(4):775-780.

[8]王姣，张英敏，李欣，等.基于惯导辅助的GPS完好性监测技术[J].弹箭与制导学报，2011，31(4)：228-231.WANG Jiao，ZHANG Ying-min，LI Xin，et al.The Research on Autonomous Integrity Monitoring Technique of GPS Based on INS[J].Journal of Projectiles Rockets Missiles and Guidance，2011，31(4):228-231.

[9]Liu H Y，Zheng G，Wang H N，et al.Research on integrity monitoring for integrated GNSS/SINS system[C]//The 2010 IEEE International Conference on Information and Automation.Harbin，China，2010:1990-1995.

[10]Bhatti U I，Ochieng W Y.Performance of rate detector algorithms for an integrated GPS/INS systems in the presence of slowly growing error[J].GPS Solutions，2012，16(3):293-301.

Optimization for multiple solution separation method in inertial aided satellite integrity monitoring

LEI Bao-quan，ZENG Jin
(AVIC XI’AN Flight Automatic Control Research Institute，Xi’an 710065，China)

An improved efficient method based on parameter sequential reuse is presented in order to reduce the computation burden of Multiple Solution Separation(MSS) method in inertial aided satellite integrity monitoring.Based on MSS method and its computational complexity analysis，a low-order processing MSS method is deduced with sequential processing.With the help of system structure and correlations of filters measurements，a filter parameter reuse method is proposed to avoid parameters replication computation.Simulation experiments are implemented by changing the fault involvement moment and visible satellite numbers，and the computational complexity between proposed method and MSS method are compared.The simulation results show that the new improved method can effectively reduce the computation burden of MSS and is convenient in practical application.

GNSS;inertial navigation;GNSS integrity monitoring;fault detection and exclusion;multiple solution separation;sequential processing;parameter reuse

U666.1

A

1005-6734(2014)03-0374-07

10.13695/j.cnki.12-1222/o3.2014.03.018

2013-11-1；

2014-04-11

航空科学基金项目（20110818013）

雷宝权（1962—），男，工学博士，研究员，从事惯性导航及组合导航研究。E-mail：yls2261@163.com