基于横坐标系的捷联惯导系统极区导航方法

李 倩 ，孙 枫 奔粤阳 于 飞

（1.哈尔滨工程大学 自动化学院，哈尔滨 150001；2.哈尔滨工程大学 理学院，哈尔滨 150001）

基于横坐标系的捷联惯导系统极区导航方法

李 倩1，2，孙 枫1，奔粤阳1，于 飞2

（1.哈尔滨工程大学 自动化学院，哈尔滨 150001；2.哈尔滨工程大学 理学院，哈尔滨 150001）

现有惯性导航系统机械编排在极区(特别是地理极点附近)不适用。针对该问题，提出了适用于捷联惯性导航系统极区使用的横坐标系导航方法。构建出横坐标系参考框架，推导出横坐标系和常规坐标系之间位置、速度和姿态信息的转换关系，建立了横坐标系捷联惯导系统的机械编排，并在此基础上分析其误差传播特性。仿真分析表明：横坐标系可以解决采用现有机械编排时，极区经线圈快速汇聚和地理极点附近无北向基准所引起的问题，从而满足极区导航要求；同时，仿真结果验证了横坐标系捷联惯导系统中位置和航向误差漂移的特性。

捷联惯性导航系统；极区；横坐标系；误差特性

基于极区工作环境特殊，以及水下潜器自主性和隐蔽性要求的考虑，惯性导航系统（Inertial Navigation System，INS）应作为极区水下潜器导航设备的核心[1-4]。目前，惯性导航系统普遍采用的机械编排是当地水平指北方位机械编排，即采用东-北-天(ENU)地理坐标系作为导航坐标系。对于平台式惯性导航系统，这种机械编排下的导航系y轴要始终指向真北。当水下潜器通过地理极点附近时，真北很快变化180°，此时导航系y轴指向变化的速率将会无穷大[5-6]。对于捷联式惯导系统，则在地理极点处存在计算溢出的问题。所以，这种机械编排不适用于在极区工作，而只能工作在南北纬度70° 以内。针对当地水平指北方位机械编排在高纬度地区存在的问题，游动方位惯导系统和自由方位惯导系统被提出[7-8]。它们可以解决惯性导航系统在极区遇到的部分问题，但由于极区经线圈的快速汇聚会使得系统导航精度随纬度的升高而下降。同时在地理极点附近，由于真北方向失去定义导致自由方位角和游动方位角失去定义，航向无法给出，即采用这两种机械编排的惯性导航系统在地理极点附近仍然无法导航。

为了解决上述机械编排在极区遇到的问题，国外首先提出了横坐标系的概念[9-10]，国内文献也指出横坐标系可以应对惯性导航系统高纬度工作的问题[11]。但他们没有对横坐标系下惯性导航系统的机械编排、误差分析进行详细的论述，同时，也未考虑到系统极区横坐标系和常规系导航参数切换的问题。针对上述问题，对基于横坐标系的捷联惯性导航系统极区工作方法进行深入研究。

1 横坐标系统定义

横坐标系统包括横地球坐标系和横地理坐标系，同时在横坐标系的参考框架下，横极轴、横赤道平面、横本初子午面以及横经纬度都需要重新定义。

在此基础上，定义指向横极轴的方向为新北向，则可以建立新的横地理坐标系，即横东-北-天坐标系，其定义如下：

——与轴呈右手定则关系；

——指向新北向；

——沿垂直方向指向天向；各坐标系示意图如图1所示。

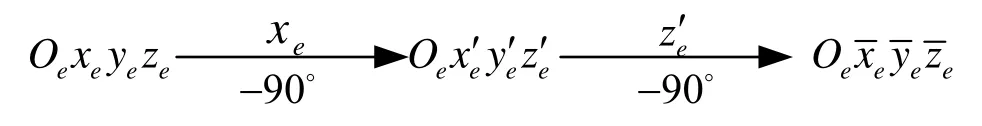
根据以上转换关系，可以利用方向余弦矩阵推导得到横地球坐标系和原地球坐标系之间的转换关系为：

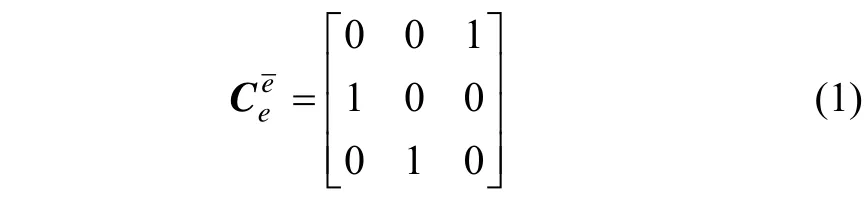
图1 横坐标系统定义Fig.1 Definition of transversal coordinate

2 导航参数在不同坐标系中的转换关系

当水下潜器在低纬度地区航行时，一般仍然使用当地水平指北方位惯导系统机械编排(以下简称为常规坐标系统机械编排)；当水下潜器由低纬度地区向极区航行时，需要将捷联惯导机械编排切换至横坐标系机械编排。为了保证系统在机械编排切换时不发生超调现象，使系统在两种机械编排间平稳过渡，需要将两种机械编排中的导航参数进行精确的转化，包括位置信息、速度信息以及姿态信息。

2.1 位置信息转换

首先分析常规坐标系统中的经纬度坐标(λ，φ)与横坐标系统中的横经度、横纬度之间的转换关系。图2为常规坐标系统中的经纬度定义与横坐标系统中的经纬度定义示意图。

如图2所示，左图是常规坐标系统中利用经纬度坐标(λ，φ)表示的载体位置P，载体与地心距离为连线，则在地球坐标系中三轴投影为：

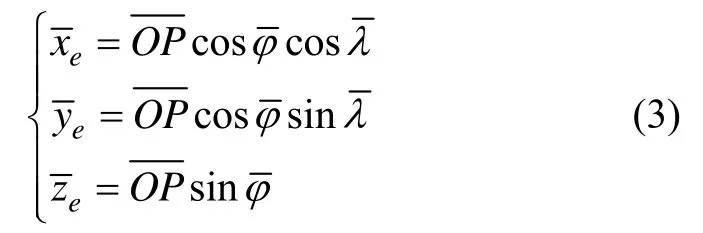
图2 常规坐标系统和横坐标系统中的经纬度坐标Fig.2 Longitude and latitude in normal and transversal coordinate system

将式(2)(3)带入式(4)得到：

2.2 速度信息转换

由于我们所需的速度信息是相对于地理系而言的，所以速度信息的转换即意味着地理坐标系和横地理坐标系之间的转换。这两个坐标系之间的转换关系可以利用方向余弦矩阵表示，进一步分解方向余弦矩阵可以得到：

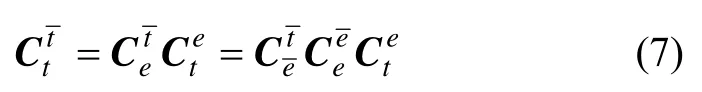
2.3 姿态信息转换

另外一种更加直观的姿态信息转换方式是利用球面三角形相关理论确定两个坐标系统中姿态信息的关系。由于轴和zt轴重合，所以两个坐标系统中的水平姿态角相同，即

下面通过在地球表面上定义几个球面角来描述横坐标系统中的航向角和常规坐标系统中航向角ψ之间的关系，如图3所示。

由图3可知，由P、A、B三点构成的球面三角形中的三个内角分别为：

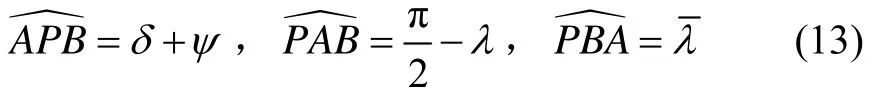
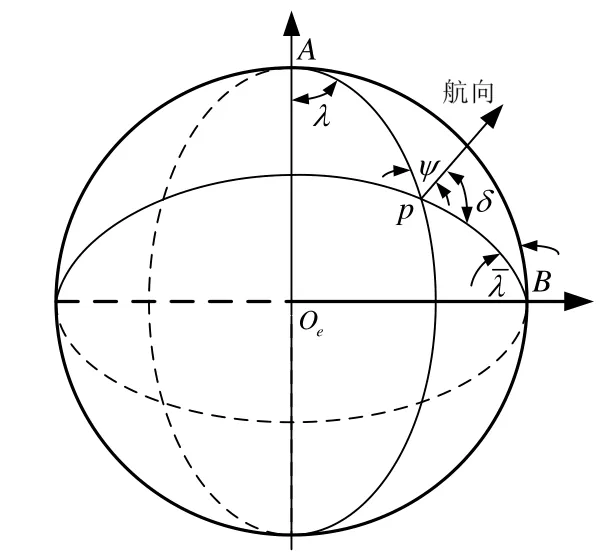
图3 航向角在两个坐标系统中的关系Fig.3 Relationship of heading angle between two coordinate systems

将式(13)中第1式代入式(14)得到：

由球面三角形正弦定理可知：

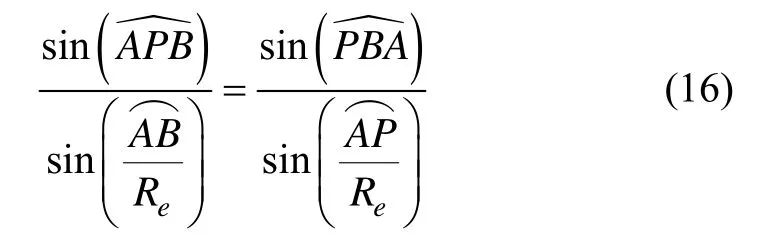
式中，Re为地球半径。由式(16)可以得到：

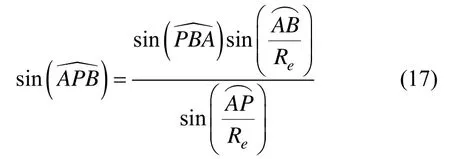
将式(18)代入(17)得到：

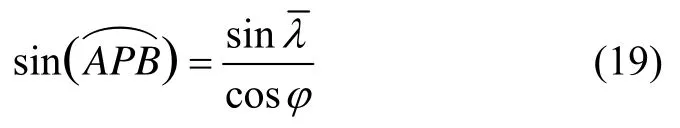
同理，利用球面三角形余弦定理可知：

由式(19) (21)可以得到：

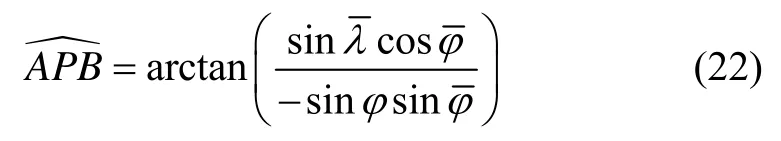
3 横坐标系捷联惯导系统机械编排及误差分析

在横坐标系捷联惯导系统中，系统机械编排基本不变。但是由于横地球坐标系和横地理坐标系相对常规坐标系统发生了改变，导致数学平台旋转角速度的计算发生了改变。

3.1 系统机械编排及误差方程

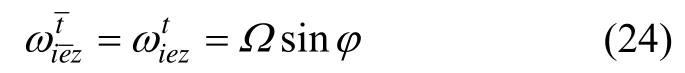
式中，Ω为地球自转角速率。将式(6)代入，得到：

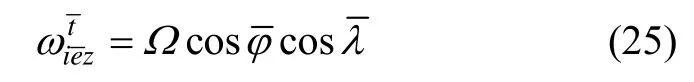
另外，由于地球自转角速度在横赤道面上，得到：

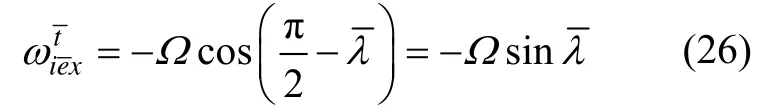
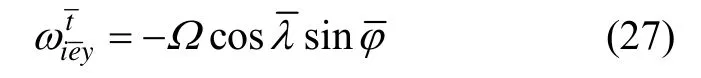
综上可得，地球转动引起的横地理坐标系角速度为：

根据式(28)(29)可以得到横地理坐标系的角速度，即控制数学平台的旋转角速度为：

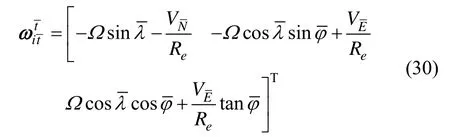
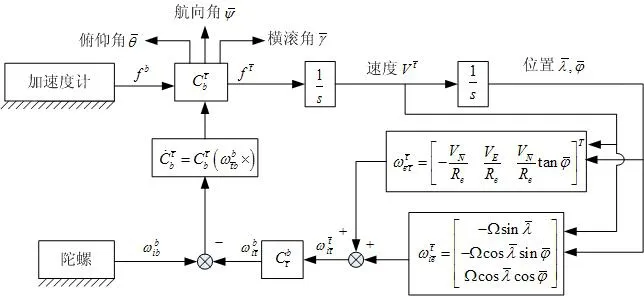
图4 横坐标系统机械编排Fig.4 Mechanization of transversal coordinate system

根据系统机械编排，可以得到静基座横坐标系捷联惯导系统误差方程如下所示：

a.失准角误差方程

b.速度误差方程

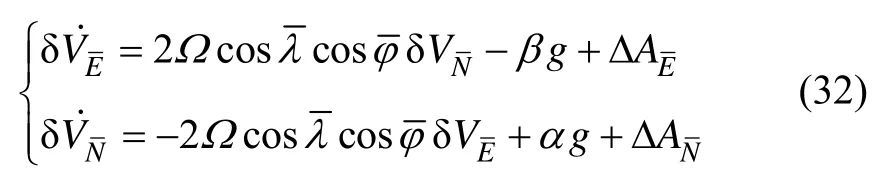
c.位置误差方程

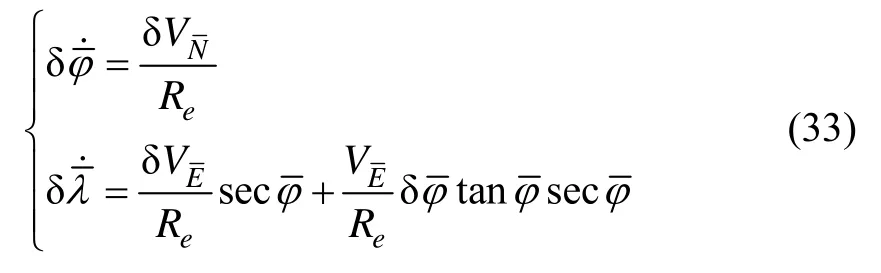
式中，α，β，γ为横坐标系统中的失准角；为横坐标系统中速度误差；为横经纬度误差；分别是陀螺漂移和加速度计零偏在横地理坐标系上的投影分量。

从式(31)～(33)可以看出，与常规坐标系统不同，横坐标系统中的经度误差不再是独立的，而是耦合到其他误差项中。

3.2 误差分析

将式(31)～(33)进行拉式变换，并写成矩阵形式，然后计算其行列式特征根为：

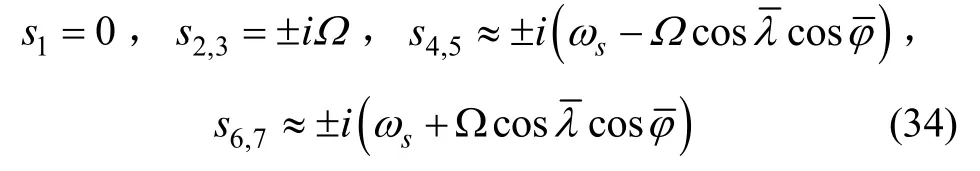
从系统特征根可以看出在横坐标系统中，同样存在舒勒、傅科以及地球三种周期性振荡。

下面分析误差源所引起的系统误差。为简化分析，这里只考虑陀螺常值漂移为唯一误差源，以经纬度误差为例。通过解矩阵方程，得到纬度误差和陀螺漂移之间的关系为

式中，

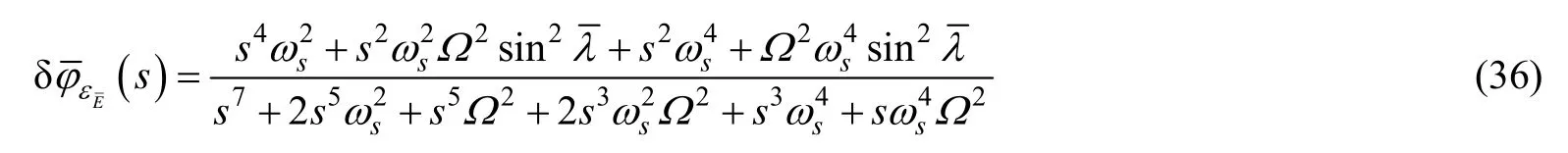
式中，sω为舒勒角频率。

将式(36)～(38)进行拉式反变换并将振荡项去掉，只考虑稳态误差得到：

同理，可以得到横经度误差在时域中的稳态值表达式为：

从式(39)(40)可以看出在横坐标系统中，横纬度误差和横经度误差都是随时间发散的，这与常规坐标系统中只有经度误差发散是不同的。同理，利用此方法分析陀螺漂移对横坐标系统中失准角的影响，发现方位失准角也是随时间发散的，这与常规坐标系统也不一样。

4 系统误差的分析比较

第3.2节分析了横坐标系统中的横经纬度误差的传播特性，下面通过将横经纬度误差转换到常规坐标系统中，比较两个坐标系统中导航参数的误差传播特性。由式(6)可知，地理纬度φ和横纬度φ、横经度λ存在下列关系：

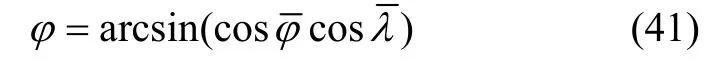
由误差传递公式可知，地理纬度误差和横经纬度误差之间存在关系：

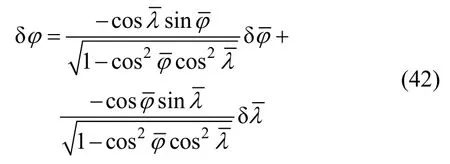
将式(39) (40)代入式(42)中，得到：

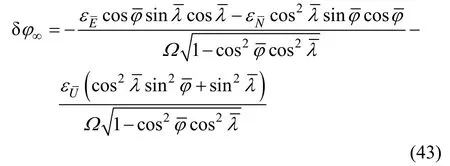
由式(43)可见，当将横坐标系统中的横纬度转换到常规坐标系统中后，转换后的纬度误差中的随时间累积项被抵消掉，导致其只存在常值性误差。为进一步比较，同时为简便分析，令

式中，ψ为常规坐标系统中的航向角，δψ为两坐标系统中航向角差值，由式(23)确定。则载体系陀螺漂移和横地理系陀螺漂移投影存在下面关系：

将式(46)代入式(43)，得到：

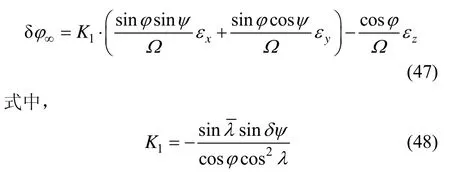
同理，可以得到转换后的经度稳态误差和载体系陀螺漂移之间存在关系：

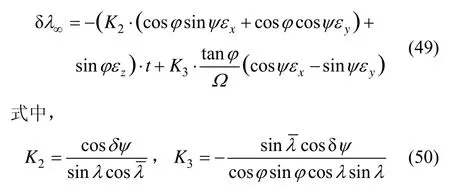
由式(49)可见，在将横经度转换到常规坐标系统中后，其误差中仍然包括常值性误差项和随时间累积误差项。

对比常规当地水平指北方位捷联惯导系统，其中的经纬度稳态误差和载体系陀螺漂移存在下面关系：

比较式(47)(49)和(51)(52)可以发现，在将横坐标系统中的横经纬度转换到常规坐标系统后，其误差与常规坐标系统中的经纬度误差具有相同的传播形式。特别是z轴陀螺对两种坐标系统影响是一致的，而x，y轴陀螺漂移对经纬度误差的影响和对横经纬度误差的影响之间只相差一个比例系数Ki(i=1，2，3)，其大小只与位置有关。如果，则x，y轴陀螺漂移对转换后的经纬度误差影响较大；如果，则x、y轴陀螺漂移对常规当地水平固定指北方位系统中的经纬度误差影响较大；如果，则x，y轴陀螺漂移对两者影响相同。

为进一步比较陀螺漂移对两者影响的关系，建立极区附近的一块矩形区域网格，其大小为20×179点，分辨率是1o。网格区域范围是：

注意，为了保证Ki(i=1，2，3)计算的有效性，没有包括纬度90°和经度180°。在此位置范围内，计算Ki(i=1，2，3)的大小，如图5～7所示。

图5 K1取值范围Fig.5 Value of K1

图6 K2取值范围Fig.6 Value of K2

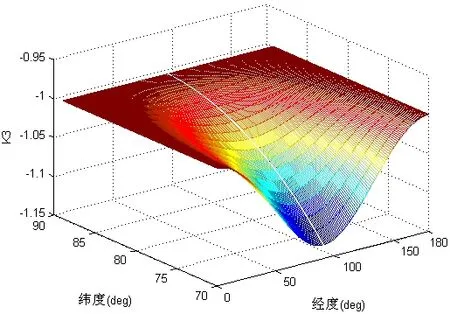
图7 K3取值范围Fig.7 Value of K3

从图5～7可以看出，越接近于极区，Ki(i=1，2，3)越接近于1，即当都以当地水平坐标系为参考基准时，两种坐标系统中的位置误差具有相同的传播特性。

5 仿真试验

为验证基于横坐标系的捷联惯导系统极区工作性能，进行仿真试验。其中，为避免数值求解在极区遇到的问题，在生成仿真轨迹时陀螺和加速度计的输出通过解析法给出。

仿真参数设置如下：初始位置φ=87°，λ=120°，载体匀速航行，速度VE=0 m/s，VN=25 m/s，航向角ψ= 0°，水平姿态角为0°，即沿着当地经线圈航行(注：此处所设置参数均相对于常规坐标系统)。捷联惯导系统工作在横坐标系机械编排，载体航行大约3.7 h后穿越极点，仿真时间4 h。误差源只考虑陀螺常值漂移，设，仿真结果如图8～10所示。由图8～10可知，在极区使用横坐标系机械编排，可以有效的解决极区经线圈快速汇聚所引起的问题，满足极区导航要求。另外，在过极点时，横坐标系捷联惯导系统仍然可以正常工作，无跳变现象发生。同时，也可以验证前面分析的结论，即横经纬度误差和航向角误差是发散的。这也说明，为了保持水下潜器长航时高精度的导航要求，有必要进一步利用重调或组合技术抑制位置误差和航向角误差发散。

图8 横坐标系速度误差Fig.8 Velocity error of transversal coordinate system

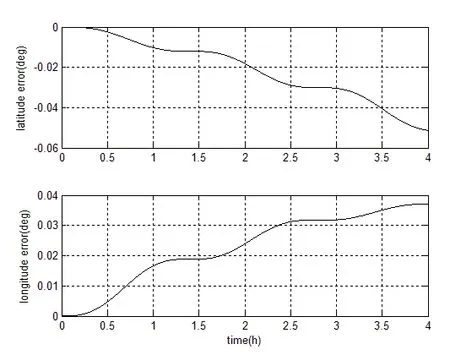
图9 横坐标系位置误差Fig.9 Position error of transversal coordinate system

图10 横坐标系姿态角误差Fig.10 Attitude error of transversal coordinate system

6 结 论

横坐标系捷联惯导系统将极点设置于赤道平面，从而解决了常规机械编排在极区进行导航时遇到的问题（特别是极点附近无北向基准）。本文给出了导航参数在横坐标系和常规系之间的转换关系；在建立横坐标系捷联惯导系统机械编排的基础上，对其进行了误差分析，结果表明在横坐标系捷联惯导系统中经纬度误差和方位失准角都是发散的。为了进一步比较陀螺漂移对两种机械编排的影响，以经纬度误差为例，将横经纬度误差转换到常规坐标系中，分析结果显示它们具有相同的误差传播形式。

仿真和分析结果表明：为保证水下潜器在极区可以长航时高精度导航，需要利用重调或组合技术抑制其误差发散，因此，研究横坐标系的组合与重调是下一步工作的重点。

（References）：

[1]Encyclopedia of Earth sciences series-polar ocean navigation[M].New York:Springer Science Business Media，2014.

[2]Andriani S，Lysandros T.Choosing a suitable projection for navigation in the arctic[J].Marine Geodesy，2013，36(2):234-259.

[3]Wang Xianwei，Cheng Xiao，Hui Fengming，et al.Navigation in fast ice near the Zhongshan Station，Antarctica[J].Marine Technology Society Journal，2013，48(1):84-91.

[4]Andreev A G，Ermakov V V，Mafter M B.High latitude trials of modern russian marine compasses[C]// Position Location and Navigation Symposium.2006:636-644.

[5]吴枫，秦永元，周琪.机载武器极区传递对准算法[J].中国惯性技术学报，2013，21(2)：141-146.WU Feng，QIN Yong-yuan，ZHOU Qi.Airborne weapon transfer alignment algorithm in polar regions[J].Journal of Chinese Inertial Technology，2013，21(2):141-146.

[6]周琪，秦永元，严恭敏，等.大飞机极区惯性/天文组合导航算法研究[J].系统工程与电子技术，2013，35(12)：2559-2565.ZHOU Qi，QIN Yong-yuan，YAN Gong-min.Stellarinertial navigation for transpolar large aircraft[J].Systems Engineering and Electronics，2013，35(12):2559-2565.

[7]周琪，岳亚洲，张晓冬，等.极区飞行间接格网惯性导航算法[J].中国惯性技术学报，2012，22(1)，18-22，66.ZHOU Qi，YUE Ya-zhou，ZHANG Xiao-dong，et al.Indirect grid inertial navigation mechanization for transpolar aircraft[J].Journal of Chinese Inertial Technology，2014，22(1):18-22，26.

[8]刘文超，谭志杨，卞鸿巍，等.游动方位 INS/GPS组合导航在极地地区的应用[J].火力与指挥控制，2013，38(2)：69-75.LIU Wen-chao，Tan Zhi-yang，BIAN Hong-wei.Application of wander azimuth INS/GPS integrated navigation in polar region[J].Fire Control&Command Control，2013，38(2):69-75.

[9]Broxmeyer C.Inertial navigation system[M].New York:McGraw-Hill，1964.

[10]Levinson E，Ter Horst J，Willcocks M.The next generation marine inertial navigation is here now[C]// IEEE Position Location and Navigation Symposium.1994:121-127.

[11]周琪，秦永元，付强文，等.极区飞行格网惯性导航算法原理[J].西北工业大学学报，2013，31(2)： 210-217.ZHOU Qi，QIN Yong-yuan，FU Qiang-wen.Grid mechanization in inertial navigation system for transpolar aircraft[J].Journal of Northwestern Polytechnical University，2013，31(2):210-217.

Polar navigation of strapdown inertial navigation system based on transversal frame in polar region

LI Qian1，2，SUN Feng1，BEN Yue-yang1，YU Fei2
(1.College of Automation，Harbin Engineering University，Harbin 150001，China;2.College of Science，Harbin Engineering University，Harbin 150001，China)

The present mechanizations of inertial navigation system are not suitable for use in polar region，especially at near the geography polar.To solve this problem，a navigation method based on transversal frame is proposed for strapdown inertial navigation system in polar region.The navigation reference framework of the transversal frame is constructed.The parameter transformations from a transversal frame system to a normal system for position，velocity and attitude are deduced.Moreover，the mechanization based on transversal frame for strapdown inertial navigation system is established，and its error propagation characteristics are analyzed.The simulation and analysis results show that this method could solve the problem that longitude circles converges fast in polar region and the north benchmark is invalid，so it can satisfy the requirements of polar navigation.Meanwhile，the simulation results also demonstrate that the yaw and position errors drift with time in the transversal frame of strapdown inertial navigation system.

strapdown inertial navigation system;polar region;transversal frame;error characteristics

U666.1

A

1005-6734(2014)02-0288-08

10.13695/j.cnki.12-1222/o3.2014.03.003

2013-11-20；

2014-03-28

高等学校博士学科点专项科研基金（20102304110021）；中央高校基本科研业务费专项基金（HEUCF041420）

李倩（1983—），女，博士研究生，从事惯性导航研究。E-mail：liqianheu@163.com

联 系 人：孙枫（1964—），男，教授，博士生导师，从事惯性导航研究。E-mail：benpao2002heu407@163.com