单轴旋转INS/GPS组合导航中重力垂线偏差引起的姿态误差分析
2014-07-20战德军戴东凯张忠华王省书黄宗升
战德军,戴东凯,张忠华王省书,黄宗升
(1.中国卫星海上测控部,江阴214431;2.国防科学技术大学 光电科学与工程学院,长沙 410073)
单轴旋转INS/GPS组合导航中重力垂线偏差引起的姿态误差分析
战德军1,2,戴东凯2,张忠华1,王省书2,黄宗升2
(1.中国卫星海上测控部,江阴214431;2.国防科学技术大学 光电科学与工程学院,长沙 410073)
重力垂线偏差是高精度惯性导航中的一个主要误差源。在INS/GPS组合导航系统中,由于GPS可以提供位置和速度修正信息,垂线偏差对组合导航系统精度的影响主要体现在姿态上。从惯性导航系统的误差方程出发,推导INS/GPS组合导航姿态估计误差和陀螺零偏估计误差的解析表达式,从理论上分析组合导航模式下垂线偏差对姿态误差的影响。通过仿真验证理论分析的正确性。分析结果表明:东向姿态误差角由北向垂线偏差决定,北向姿态误差由东向垂线偏差决定;航向误差受东向垂线偏差和北向垂线偏差的一阶导数的共同影响,垂线偏差的剧烈变化将引起较大的航向误差。
垂线偏差;组合导航;姿态;单轴旋转
由于地球形状的不规则、地形的起伏以及密度分布不均等因素,实际的重力场与正常重力模型之间存在差异称为重力扰动,其垂直分量称为重力异常,水平分量体现为垂线偏差。重力扰动误差,特别是垂线偏差(deflection of the vertical,DOV)是惯性导航系统(INS)的一个重要的误差源[1]。在中低精度导航应用中,由于惯性器件自身的误差相对较大,采用正常重力模型即可满足需求。然而,高精度惯性导航系统中,随着惯性器件的精度不断提高,重力扰动误差的影响逐渐突显出来[2],成为惯性导航中最主要的误差因素。
在INS/GPS组合导航的模式下,由于GPS可以提供位置和速度修正信息,垂线偏差对组合导航系统的影响主要体现在姿态误差上。垂线偏差一般为几角秒,在一些地形变化剧烈的区域(如山脉、海岛、海沟等)甚至大于 1′[3],在没有进行精确补偿的情况下将引起较大的系统姿态误差,这在高精度测绘、航天测控等[3-4]更为关注姿态测量精度的应用中是尤其需要引起重视的。利用单轴旋转式INS[5]与GPS组合导航可以显著提高系统的可观测度,减小甚至消除惯性器件零偏水平分量的影响,但对垂线偏差误差则无法抑制和消除。
本文在惯性导航误差模型的基础上,从理论上分析垂线偏差对单轴旋转 INS/GPS组合导航系统的影响,推导了组合导航姿态误差和陀螺零偏估计误差的解析表达式,并通过仿真对理论分析的结论进行验证。
1 单轴旋转INS/GPS组合导航中垂线偏差引起的姿态误差的理论分析
为了便于分析,本文假定惯性器件中只存在零偏误差,只讨论载体匀速运动的情况。在当地地理坐标系n系下,惯性导航系统的误差方程[6]为式(1)~(4)。
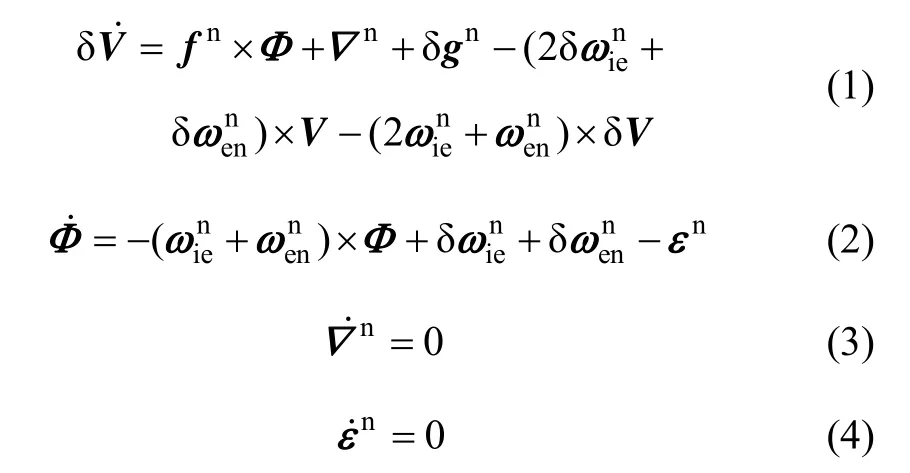
式中:δV为速度误差,nf为n系下的比力,Φ为姿态误差角,是n系下等效加表零偏,是重力扰动矢量,为地球自转角速度,为n系相对于地球坐标系 e的旋转角速度,分别为和的误差,是n系下等效陀螺零偏。
1.1 垂线偏差引起的水平姿态误差分析
在组合导航模式下,速度误差和位置误差都是可以直接观测的状态量,因此可令:
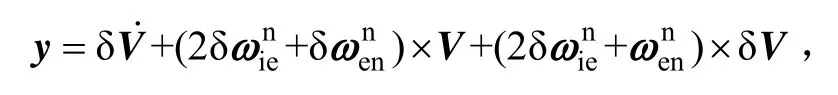
此时,式(1)可化简为:

由于惯性导航系统中天向速度通道与水平通道是解耦的[7],这里只分析水平通道的速度误差。将式(5)写为分量的形式如下:

式中:下标E、N、U分别表示东向、北向和天向分量。东向和北向的垂线偏差定义为 :,。
由于载体沿水平方向匀速运动,fU=g,。在单轴旋转式惯导系统中,加表零偏的水平分量▽E、▽N是可观测的[8],将式(6)(7)改写为:
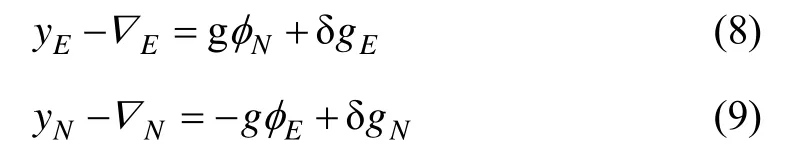
式(8)(9)左边均为可观测量,姿态误差的估计值可写为如下形式:


由式(12)(13)可知东向和北向姿态误差角分别由北向和东向垂线偏差分量直接决定。
1.2 垂线偏差引起的航向姿态误差分析
航向误差和陀螺零偏估计误差可通过式(2)求解。式(2)中为可观测量,且数值较小,可以忽略其影响,将式(2)简化并写为分量的形式如下:

以下将分别讨论东向和北向垂线偏差对δUφ和δUε的影响。
1.2.1 只存在北向垂线偏差
该条件下有:

由式(18)可知Nφ为可观测状态。此外,在单轴旋转式惯导系统中,陀螺零偏的水平分量Eε、Nε是可观测的[8],由式(10)(14)得:

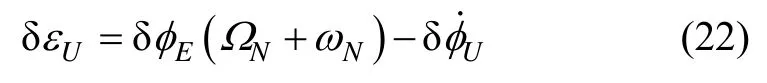
将式(17)(21)代入(22)得:
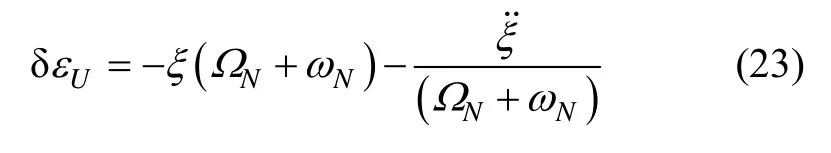
1.2.2 只存在东向垂线偏差
在该条件下可得到水平姿态误差为:

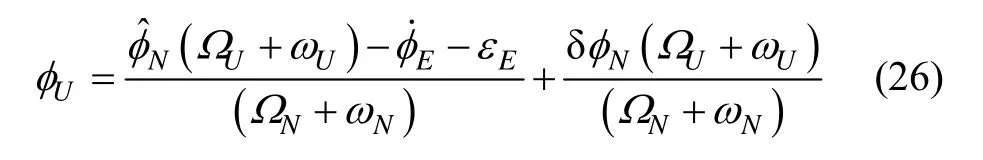

由式(16)得:
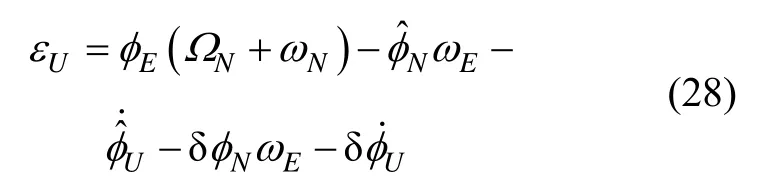
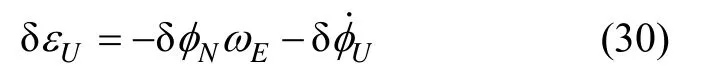
将式(24)(27)代入式(30)得:

2 数值仿真
本节将通过仿真对以上理论分析进行验证。
2.1 仿真条件
1)设置载体的初始位置为北纬45°,东经120°,高度为0 m,以14 kn的速度匀速沿东向航行,航行中保持高度和航向不变。单轴旋转惯导系统采用两位置、四次序调制方案,停止时间设为270 s。仿真的采样频率为20 Hz。
2)仿真中设定陀螺常值零偏为0.01(°)/h,为了便于分析常值零偏的估计误差,假定陀螺角度随机游走较小,将其设置为0.000 02 (°)/√h;加表的常值零偏为20 μg,噪声为 1 μg/√s;GPS 的速度精度为 0.03 m/s,位置精度为2 m。
3) 在正常重力模型的基础上加入东向和北向的垂线偏差,以下将分别讨论不同垂线偏差条件下单轴旋转INS/GPS组合导航系统的姿态误差。
2.2 只存在北向垂线偏差的情况
由式(21)(23)可知,在只存在北向垂线偏差的情况下,航向估计误差和天向陀螺的零偏估计误差分别由决定。为验证该理论,设置航迹上的垂线偏差分布如下:设置航迹上的北向垂线偏差ξ的分布如图1所示:在航行前4 h内设置ξ=0,此后以0.0005 (″)/s的速率匀速增大,当ξ增大到15″后保持8 h,此后以0.0005 (″)/s的速率匀速减小到1″。
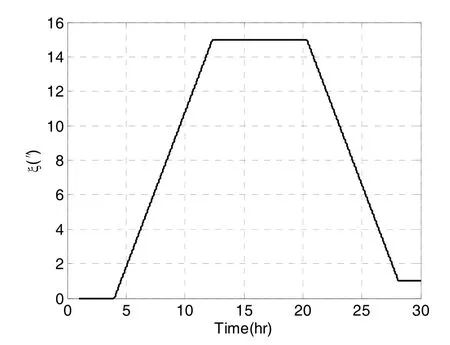
图1 航迹上北向垂线偏差的分布Fig.1 Distribution of DOV north component on the trace
仿真利用Kalman滤波实现INS/GPS的组合导航,组合导航选取为状态量,不对北向垂线偏差ξ建模,选取GPS和INS输出的速度之差作为观测量。仿真得到的组合导航系统的姿态估计误差如图2所示:载体的北向姿态误差为,东向姿态误差很好地跟踪ξ的变化。航向误差在1~4 h内接近0,随着ξ的匀速增大迅速收敛到-10″;当ξ继续保持15″不变时,迅速减小到3″;此后ξ匀速减小,也随之迅速地收敛到8″。该仿真的结果表明:主要受北向垂线偏差的一阶导数的影响,与式(21)得出的结论是一致的。

图2 INS/GPS组合导航的姿态测量误差Fig.2 Attitude errors of INS/GPS integrated navigation
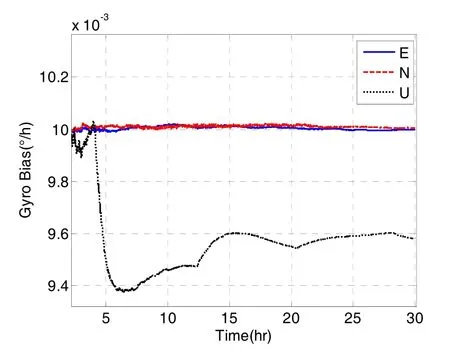
图3 陀螺零偏估计结果Fig.3 Estimation result of gyro biases system
图3为仿真得到的组合导航系统的陀螺零偏估计结果。仿真结果表明:当惯导系统采用单轴旋转调制时,东向和北向陀螺零偏估计精度较高,但天向陀螺的零偏误差受ξ的影响较大,在4 h处仿真得到的误差迅速增大到约为6e-4 (°)/h,在该时刻北向垂线偏差变化率˙由0突变到0.0005 (″)/s。考虑采样时间为 20 Hz 该时刻˙=0.01 (″)/s2,由式(23)可计算得到。该理论计算的结果与仿真结果一致项为小量,影响较小。
为了进一步验证北向垂线偏差对航向误差的影响,本文仿真了不同北向垂线偏差变化速率下航向误差角的响应情况,设置航迹上的垂线偏差分布在航行前4 h内为ξ=0,此后分别以0.0002 (″)/s、0.0006 (″)/s、0.0010 (″)/s的速率匀速增大,仿真的结果如图4所示。仿真结果表明,随着北向垂线偏差变化速率的增大,航向误差也随之近似线性增长,当˙=0.0010 (″)/s时,在8 h时刻ξ≈12″,此时的航向误差已大于20″,因此当航迹上的北向垂线偏差变化较大时,将引起严重的航向姿态误差。

图4 北向垂线偏差变化率引起的航向误差Fig.4 Yaw errors induced by derivation of north DOV
2.3 只存在东向垂线偏差的情况
设置航迹上的东向垂线偏差η分布如图5所示:在航行前4 h内设置η=0,此后以0.0003 (″)/s的速率匀速增大,当η增大到15″后保持不变。组合导航采用的滤波算法与情况一相同。仿真得到的组合导航系统的姿态估计误差如图2所示:载体东向姿态误差;北向失准角很好地跟踪η的变化,航向误差的变化趋势也基本与η一致,该结果与式(27)得出的结论相符,即在只存在东向垂线偏差时,直接由η决定的。

图5 航迹上东向垂线偏差的分布Fig.5 Distribution of DOV east component on the trace
陀螺零偏的仿真估计结果如图7所示:东向和北向陀螺零偏的估计误差都较小,天向陀螺的零偏估计误差受η的影响较大。当,缓慢收敛到接近 0.0003 (°)/h(即 0.0003 (″)/s);当时,又缓慢地向0收敛,由于收敛速度较慢,这一现象并不明显。由此可见:主要由η的一阶导数η˙决定,该结论与利用式(31)直接计算的结果相吻合(为小量,影响较小)。
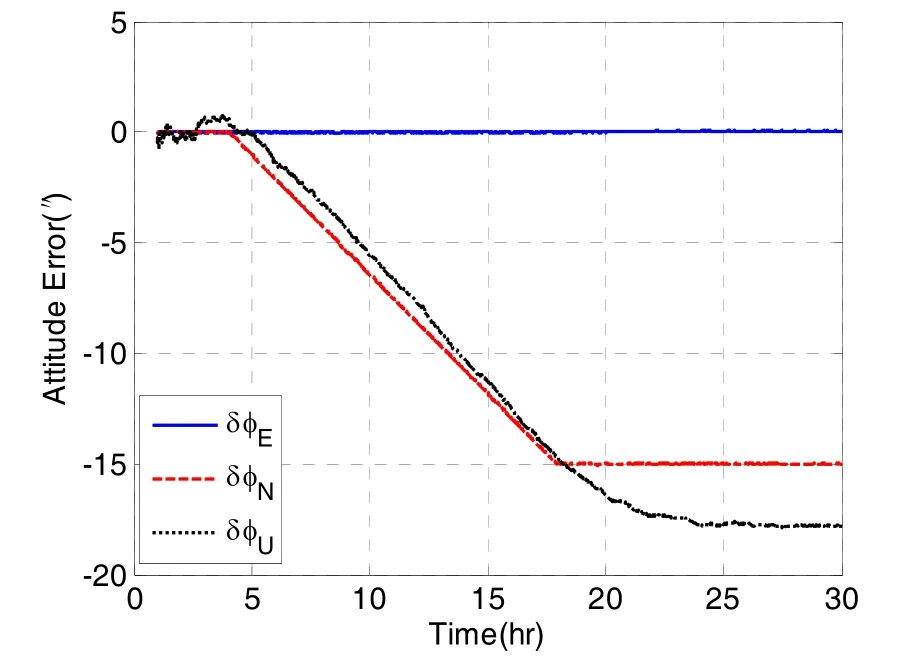
图6 INS/GPS组合导航的姿态测量误差Fig.6 Attitude errors of INS/GPS integrated navigation
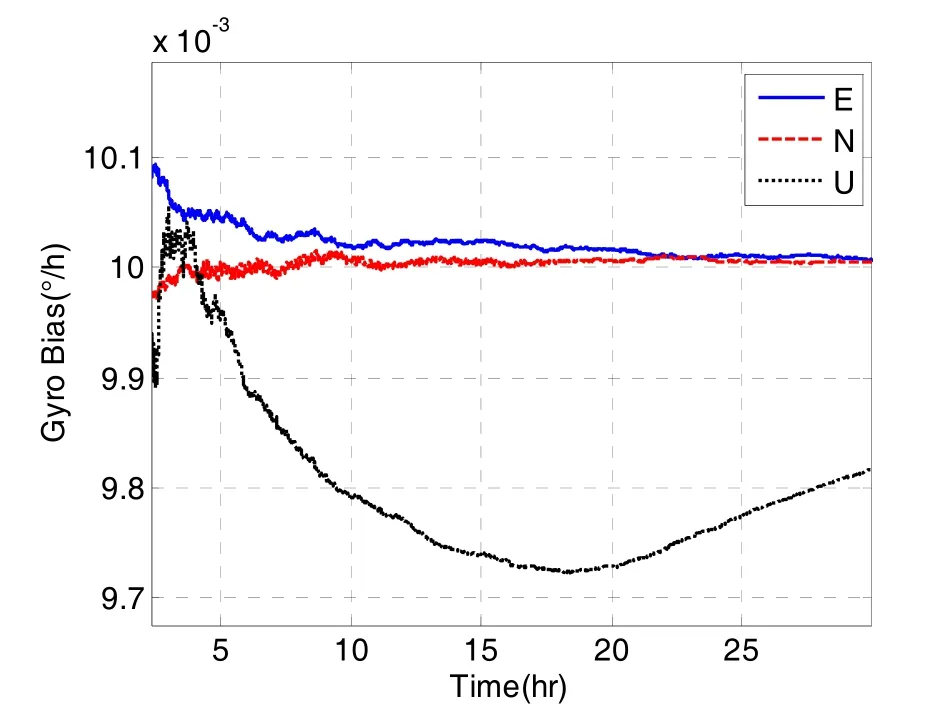
图7 陀螺零偏估计结果Fig.7 Estimation result of gyro biases
3 结 论
本文从理论上分析了INS/GPS组合导航模式下垂线偏差对系统姿态精度的影响,给出姿态估计误差的解析表达式,并通过仿真验证了理论的正确性。理论和仿真的结果表明:东向、北向姿态误差分别直接由北向、东向垂线偏差决定;航向姿态误差同时受由东向垂线偏差和北向垂线偏差变化率的影响,在某些地形复杂的区域,垂线偏差的变化较为剧烈,北向垂线偏差的快速变化将会引起很大的航向角误差。
此外,本文还分析了垂线偏差对陀螺零偏估计误差的影响,在GPS信号失锁的情况下,由垂线偏差引起的陀螺零偏估计误差将进一步影响系统的自主导航精度。本文的分析表明:在采用高精度单轴旋转惯性导航系统和GPS组合导航的情况下,由垂线偏差引起的系统姿态误差仍然无法得到抑制。因此在高精度INS/GPS组合导航系统中,垂线偏差的补偿是影响系统的姿态测量精度关键因素。
(References):
[1] 李胜全,欧阳永忠,常国宾,等.惯性导航系统重力扰动矢量补偿技术[J].中国惯性技术学报,2012.20(4):410-413.LI Sheng-quan,OUYANG Yong-zhong,CHANG Guobin,et al.Compensation technology of gravity disturbance vector in inertial navigation system[J].Journal of Chinese Inertial Technology,2012,20(4):410-413.
[2] Welker T C,Pachter M,Huffman R E.Gravity gradiometer integrated inertial navigation[C]//2013 IEEE European Control Conference(ECC).2013:846-851.
[3] Grejner-Brzezinska D A,Yi Y,Toth C,et al.On improved gravity modeling supporting direct georeferenceing of multisensor systems[C]//20th International congress for photogrammetry and remote sensing.2004:908-913.
[4] Siouris G M.Gravity modeling in aerospace applications[J].Aerospace Science and Technology,2009,13(6):301-315.
[5] 龙兴武,于旭东,张鹏飞,等.激光陀螺单轴旋转惯性导航系统[J].中国惯性技术学报,2011.18(2):149-153.LONG Xing-wu,YU Xu-dong,ZHANG Peng-fei,et al.Singlerotating inertial navigation system with ring laser gyroscope[J].Journal of Chinese Inertial Technology.2011,18(2):149-153.
[6] Blankinship K G.A general theory for inertial navigator error modeling[C]// 2008 IEEE/ION Position,Location and Navigation Symposium.2008:1152-1166.
[7] 卢鑫,练军想,吴美平.高精度舰载惯性导航系统的重力影响研究[J].导航与控制,2010,9(4): 15-21.LU Xin,LIAN Jun-xiang,WU Mei-ping.Research of gravity error compensation in marine inertial navigation system[J].Navigation and Control,2010,9(4):15-21.
[8] Wu Y,Zhang H,Wu M,et al.Observability of strapdown INS aligment:A global perspective[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(1):78-102.
Analysis of gravity vertical deflection-induced attitude error in single-axis rotation INS/GPS integrated navigation system
ZHAN De-jun1,2,DAI Dong-kai2,ZHANG Zhong-hua1,WANG Xing-shu2,HUANG Zong-sheng2
(1.China Satellite Maritime Tracking and Controlling Department,Jiangyin 214431,China;2.School of Opto-Electronic Science and Engineering,National University of Defense Technology,Changsha 410073,China)
Gravity deflection of the vertical(DOV) is one of the main error sources in high-precision inertial navigation.As the gravity-induced position error can be easily dumped in GPS/INS integrated navigation,the attitude estimation errors are more affected by DOV.In this paper,theoretical analysis of the gravity-induced GPS/INS navigation attitude errors is presented.The analytical results of attitude errors due to DOV are derived based on the inertial navigation error model,and the gyro bias estimation errors are analyzed accordingly.The numerical simulation results agree well with the theoretic analysis.The analysis results show that the east and north attitude errors are affected by north and east DOV respectively,while the yaw error is affected by east DOV and the first derivative of north DOV,meaning that the abrupt change of DOV may result in significant yaw error.
deflection of the vertical;integrated navigation;attitude;single-axis rotation
U666.1
A
1005-6734(2014)03-0301-05
10.13695/j.cnki.12-1222/o3.2014.03.005
2014-01-21;
2014-05-05
中国博士后科学基金(2012M512123);自然科学基金(61275002)
战德军(1979—),男,讲师,主要从事光电仪器与测控技术研究。Email:zdj4444@sina.com
