Gorenstein fp-平坦和强Gorenstein fp-平坦模

陈文静

(西北师范大学数学与统计学院,甘肃兰州730070)

Gorenstein fp-平坦和强Gorenstein fp-平坦模

陈文静

(西北师范大学数学与统计学院,甘肃兰州730070)

引入了Gorenstein fp-平坦模和强Gorenstein fp-平坦模的概念,讨论了这两类模的一些性质、联系以及稳定性.

Gorenstein fp-平坦模;强Gorenstein fp-平坦模;投射可解类

1 引言及准备

1969年,文献[1]对双边Noether环上的有限生成模定义了G-维数为零的模.随后,文献[2-3]引入Gorenstein投射模、Gorenstein内射模和Gorenstein平坦模的概念.2004年,文献[4]引入了投射可解类和内射可解类的概念.近年来,众多学者对这些模类进行了研究[5-7].

2000年,文献[8]引入了fp-投射模、fp-内射模和fp-平坦模的概念.实际上,fp-投射模、fp-内射模和fp-平坦模分别是投射模、FP-内射模和平坦模的推广.2011年,文献[9]研究了这三种模,并得到了这些模与一些环的等价刻画.

本文研究了Gorenstein fp-平坦和强Gorenstein fp-平坦模的一些性质、联系及稳定性.

除非特别申明,环R是具有单位元的结合环,所有涉及的模均是左酉模.对任意的模M,用M+表示模M的示性模HomZ(M,/).对未作解释的事实和概念,请参见文献[10].

称左R-模M是Gorenstein平坦模[3],如果存在一个平坦左R-模的正合列

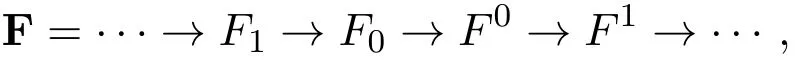
称左R-模M是弱Gorenstein内射模[7],如果存在一个内射左R-模的正合列

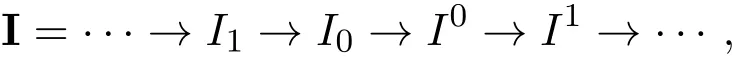
称左R-模M是强Gorenstein平坦模[6],如果存在一个投射左R-模的正合列

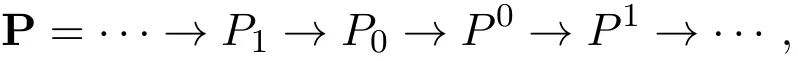
称左R-模N是fp-平坦模[8],如果对任意有限表示右R-模的单同态K→L, K⊗RN→L⊗RN是单同态.称左R-模M是fp-内射模[8],如果对任意有限表示左R-模的单同态K→L,HomR(L,M)→HomR(K,M)是满同态.对偶地可定义fp-投射模.

称左R-模M是FP-内射模[11],如果对任意有限表示左R-模

称R是左IF环[12],如果每个内射左R-模是平坦模.

2 Gorenstein fp-平坦模

定义2.1称M是Gorenstein fp-平坦左R-模,如果存在一个平坦左R-模的正合列

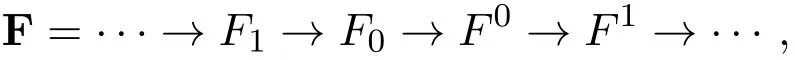
注2.1(1)每个Gorenstein fp-平坦模是Gorenstein平坦模.

(2)Gorenstein fp-平坦模类关于直和封闭.

(3)若L=………→L1→L0→L0→L1→………满足定义2.1,则由对称性可知,L的所有核、像和上核都是Gorenstein fp-平坦模.

(4)如果M是Gorenstein fp-平坦左R-模,那么对任意的fp-内射右R-模Q及正整数

(5)平坦模是Gorenstein fp-平坦模.

定义2.2称左R-模M是Gorenstein fp-内射模,如果存在一个内射左R-模的正合列

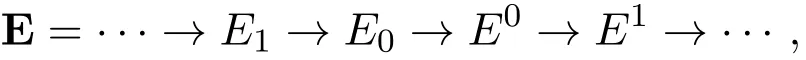
定理2.1如果M是Gorenstein fp-平坦左R-模,那么M+是Gorenstein fp-内射右R-模.

证明因为M是Gorenstein fp-平坦左R-模,所以存在平坦左R-模的正合列

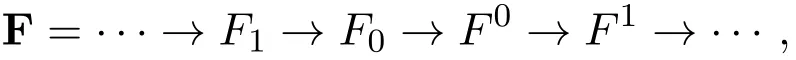
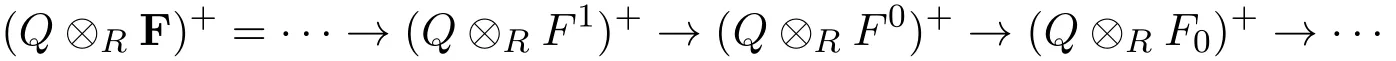
是正合的,并且

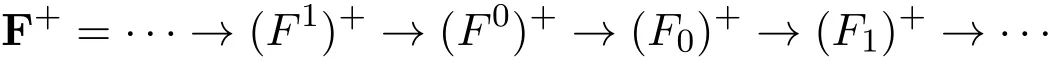
是内射右R-模的正合列,使得M+Im((F0)+→(F1)+).由伴随同构可得,

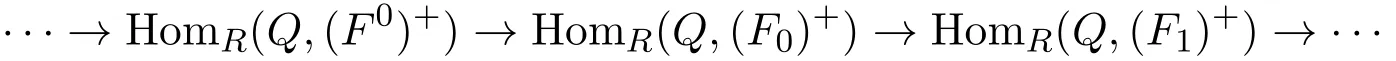
是正合的.因此,M+是Gorenstein fp-内射右R-模.

定理2.2在凝聚环上Gorenstein fp-平坦模类是投射可解类,并且关于直和项封闭.

证明类似于文献[4]中定理3.7的证明.

命题2.1设R是左Noether环.则M是Gorenstein fp-平坦右R-模当且仅

当M是Gorenstein平坦的.

证明⇒)由注2.1,结论显然.

⇐)设M是Gorenstein平坦右R-模.因为R是左Noether环,所以R是左凝聚环.故由文献[9]中定理2.4,每个fp-内射左R-模是FP-内射的.在左Noether环上FP-内射左R-模是内射的,于是在左Noether环上fp-内射左R-模是内射的.因此,M是Gorenstein fp-平坦的.

命题2.2设R是双边IF环.则每个弱Gorenstein内射模是Gorenstein fp-平坦模.

证明设M是弱Gorenstein内射模,于是存在内射模的正合列

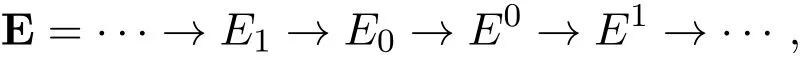
3 强Gorenstein fp-平坦模

定义3.1称M是强Gorenstein fp-平坦左R-模,如果存在一个投射左R-模的正合列

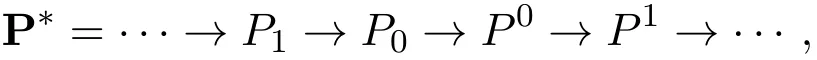
注3.1(1)强Gorenstein fp-平坦模是强Gorenstein平坦模.

(2)强Gorenstein fp-平坦模类关于直和封闭.

(3)若L=………→L1→L0→L0→L1→………满足定义3.1,则由对称性可知,L的所有核、像和上核都是强Gorenstein fp-平坦模.

(4)投射模是强Gorenstein fp-平坦模.

引理3.1M是强Gorenstein fp-平坦模当且仅当存在一个投射R-模的正合列

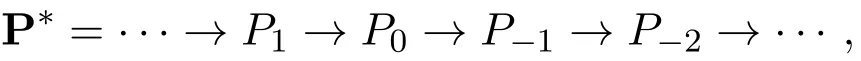
引理3.2设M是强Gorenstein fp-平坦模,Q是fp-平坦模.则有,对于i≥1,

引理3.3设M是R-模,Q是fp-平坦R-模.如果对任意正整数i有那么对于M的任意投射分解P,HomR(P,Q)是正合的.

命题3.1M是强Gorenstein fp-平坦模当且仅当存在R-模的短正合列

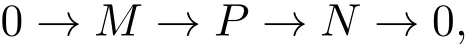
其中P是投射模,N是强Gorenstein fp-平坦模.

证明⇒)由定义3.1,结论显然.

⇐)因为N是强Gorenstein fp-平坦模,所以存在投射R-模的正合列

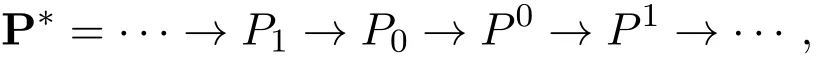
使得N～=Im(P0→P0),并且对任意fp-平坦模Q,HomR(P∗,Q)是正合的.于是存在正合列

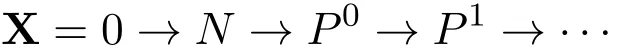
且HomR(X,Q)是正合的.由引理3.1,

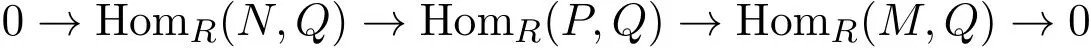
是正合的.于是可得R-模的正合列

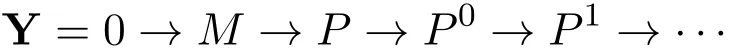
且HomR(Y,Q)是正合的.由引理3.2和引理3.3,对于M的任意投射分解Z,HomR(Z,Q)是正合的.不妨设

将Y和Z接起来可得投射R-模的正合列

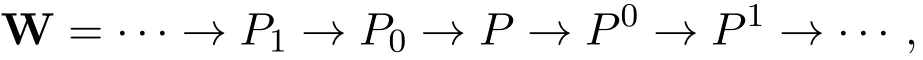
使得M～=Im(P0→P),并且HomR(W,Q)是正合的.因此,M是强Gorenstein fp-平坦模.

引理3.4设0→M′→M→M′→0是R-模的短正合列.如果M′和M′是强Gorenstein fp-平坦模,那么M也是强Gorenstein fp-平坦模.

证明类似于文献[5]中引理3.1的证明.

定理3.1强Gorenstein fp-平坦模类是投射可解类.

证明由注3.1,投射模是强Gorenstein fp-平坦模.考虑正合列

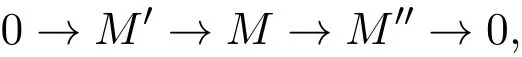
其中M′是强Gorenstein fp-平坦模.若M′是强Gorenstein fp-平坦模,则M是强Gorenstein fp-平坦模.设M是强Gorenstein fp-平坦模.则存在R-模的短正合列

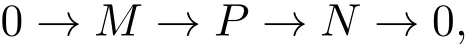
其中P是投射模,N是强Gorenstein fp-平坦模.考虑M→P和M→M′的推出:

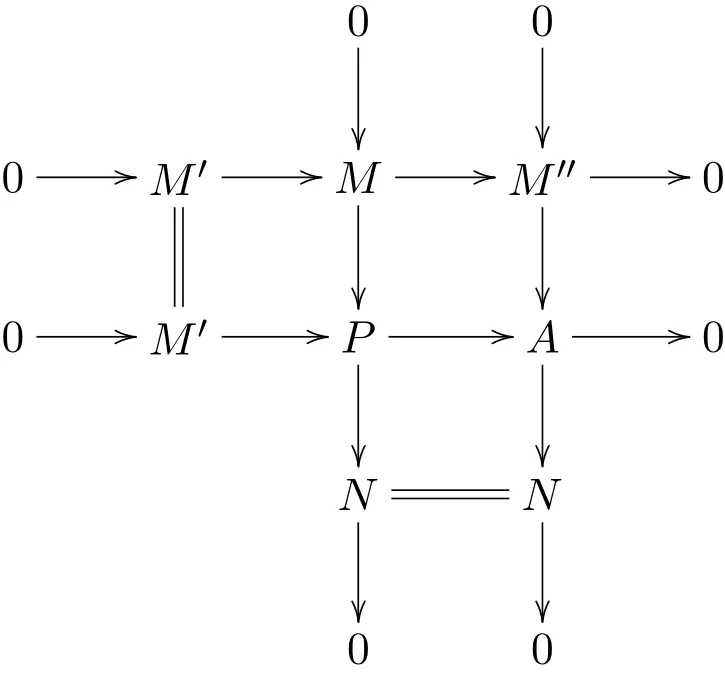
因为N和M′′是强Gorenstein fp-平坦模,所以由引理3.4,A是强Gorenstein fp-平坦模.因为P是投射模,A是强Gorenstein fp-平坦模,所以由命题3.1,M′是强Gorenstein fp-平坦模.

推论3.1每个强Gorenstein fp-平坦右R-模是Gorenstein fp-平坦右R-模.

证明由注3.1和定理3.1知,类似于文献[4]中命题1.4的证明.

定理3.2设0→M→N→L→0是R-模的短正合列.如果M和N是强Gorenstein fp-平坦模,那么L是强Gorenstein fp-平坦模当且仅当对任意fp-平坦模

证明⇒)由引理3.2,结论显然.

⇐)因为M是强Gorenstein fp-平坦模,所以存在R-模的短正合列

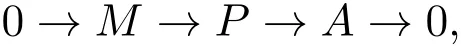
其中P是投射模,A是强Gorenstein fp-平坦模.考虑M→P和M→N的推出:

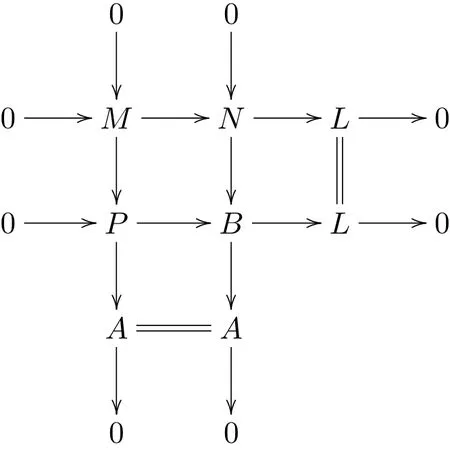
B是强Gorenstein fp-平坦模.于是存在R-模的短正合列0→B→H→C→0,其中H是投射模,C是强Gorenstein fp-平坦模.考虑B→L和B→H的推出:

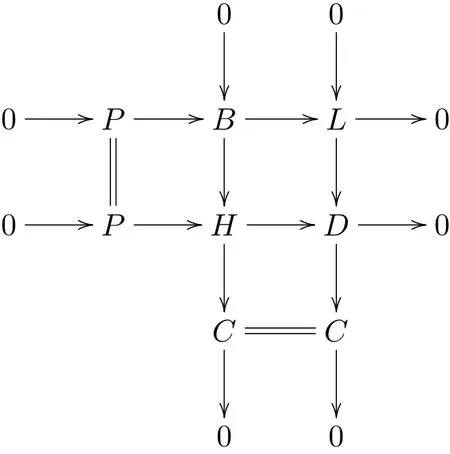
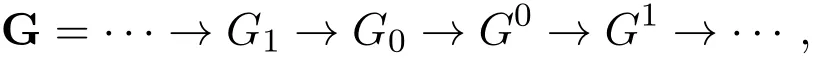
证明⇒)由定义3.1和注3.1易得.

⇐)由引理3.2和引理3.3得,对于M的任意投射分解X,HomR(X,Q)是正合的.不妨设

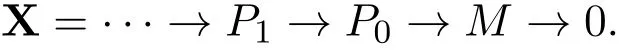
另一方面,令Ai=Im(Gi→Gi+1).因为G0是强Gorenstein fp-平坦模,所以由命题3.1,存在R-模的短正合列

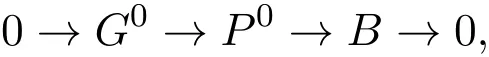
其中P0是投射模,B是强Gorenstein fp-平坦模.考虑G0→A0和G0→P0的推出:

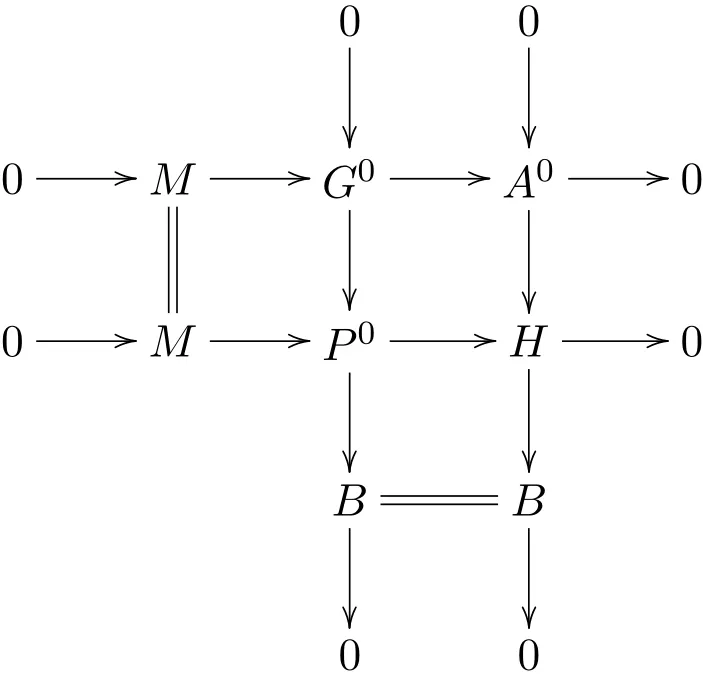
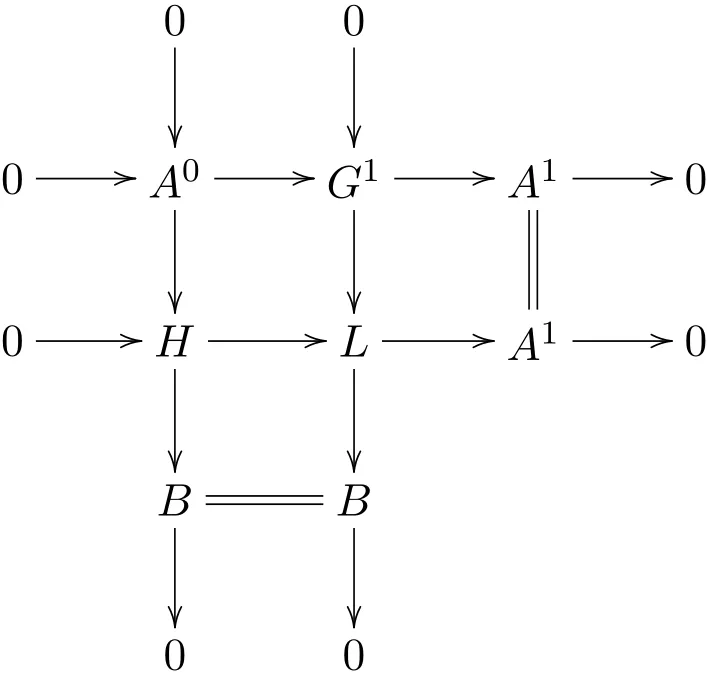
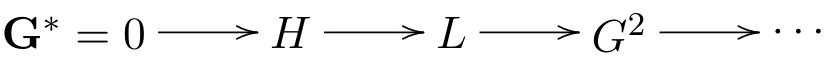
且HomR(G∗,Q)是正合的.继续同样的方法.于是可得R-模的正合列

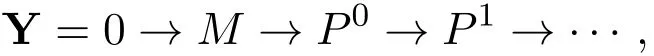
其中每个Pi是投射模,并且HomR(Y,Q)是正合的.将X和Y接起来,可得投射模的正合列

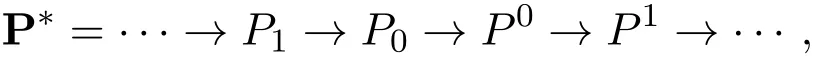
命题3.2每个强Gorenstein fp-平坦右R-模是Gorenstein fp-平坦右R-模.

证明由定义2.1,定义3.1,文献[9]中引理2.1,类似于本文定理2.1的证明.

命题3.3设R是左凝聚环.则M是强Gorenstein fp-平坦右R-模当且仅当M是强Gorenstein平坦右R-模.

证明⇒)由注3.1,M是强Gorenstein平坦右R-模.

⇐)设M是强Gorenstein平坦右R-模.因为R是左凝聚环,所以由文献[9]中定理2.4得,每个fp-平坦右R-模是平坦模.因此M是强Gorenstein fp-平坦右R-模.

[1]Auslander M,Bridger M.Stable Module Theory[M].American Mathematical Society:Providence Rbode Island,1969.

[2]Enochs E E,Jenda O M G.Gorenstein injective and projective modules[J].Math.Zeit.,1995,220:611-633.

[3]Enochs E E,Jenda O M G,Torrecillas B.Gorenstein fl at modules[J].Nanjing Daxue Xuebao Bannian Kan, 1993,10:1-9.

[4]Holm H.Gorenstein homological dimensions[J].J.Pure Appl.Algebra,2004,189(1):167-193.

[5]Enochs E E,Iacob A,Jenda O M G.Closure under trans fi nite extensions[J].Illinois J.Math.,2007,51:561-569.

[6]Ding N,Li Y,Mao L.Strongly Gorenstein fl at modules[J].J.Aust.Math.Soc.,2009,86(3):323-338.

[7]Gao Z.Weak Gorenstein projective,injective and fl at modules[J].J.Algebra Appl.,2013,12(2):3841-3858.

[8]Garkusha G A,Generalov A I.Duality for categories of fi nitely persented modules[J].St.Pet.Math.J., 2000,11:1051-1061.

[9]Mao L.Remark on fp-injective and fp- fl at modules[J].Arab.J.Sci.Eng.,2011,36:1013-1022.

[10]Rotman J J.An Introduction to Homological Algebra[M].New York:Academic Press,1979.

[11]Stenstr¨om B.Coherent rings and FP-injective modules[J].J.Lond.Math.Soc.,1970,2:323-329.

[12]Colby R R.Rings which have fl at injective modules[J].J.Algebra,1975,35:239-252.

[13]Ding N,Chen J.The fl at dimension of injective modules[J].Manu.Math.,1993,78:165-177.

2010 MSC:16D40

《纯粹数学与应用数学》稿约

1 本刊是经国家科委、新闻出版署批准公开发行的数学及其应用的综合性学术刊物,主要刊登数学学科中有创造性的研究论文和具有重要经济价值的应用性论文,以繁荣数学理论,推进应用数学研究.本刊2000年荣获《CAJ-CD规范》执行优秀奖,2004年入选全国中文核心期刊,2006年获陕西省出版编辑良好奖.2012年11月获陕西省科技期刊编辑学会2011-2012年度优秀科技期刊奖.

2 本刊只接收中文稿件，2010起为双月刊,每年一卷,共6期,国内外公开发行.

3 来稿要求和注意事项

3.1 来稿必须包括：题目、作者姓名、作者单位(全称)、作者简介(性别、年龄、职称、学位及主要研究方向)、中文摘要(200字左右)、关键词(3-5个)、中图分类号、2000年美国《数学评论》主题分类号、英文摘要、正文、参考文献.如有基金项目资助,请在文稿首页注明批准文号.

3.2 节段序号分别用1;1.1;1.1.1表示,稿件内容力求精炼充实,表述正确.摘要应说明论文的目的、方法、结果，结论和作用等.英文摘要必须与中文摘要一致,摘要中不出现公式与参考文献标识,尽量用语言叙述所得主要结果.摘要正文请用第三人称表述,

3.3 外文字母必须分清大小写、黑体(黑正体、黑斜体)、白体(白正体、白斜体)、花体;上下标的字母、数字和符号,其位置要区分明显,文中不要用同一个符号表示不同的意思.务请注明作者的联系电话和电子信箱.

3.4 文中插图请用描图纸黑墨绘制或由计算机打出,插图要清楚,线条均匀,要有图题;表格用三线表,要有表题;图、表要有中英文对照的图题和表题.

3.5 参考文献按文中引用的先后顺序编号,未公开发表的资料请勿引用.文献书写格式如下：

(1) 书籍:作者(姓在前).书名[M].版次(初版不写).出版地:出版社,出版年．

(2) 书籍中的析出文献:作者(姓在前).论文题名[M]//专著责任者.专著题名.出版地:出版社,出版年:起止页码.

(3) 译著:原作者(姓在前).书名[M].版次(初版不写).译者姓名.出版地:出版社,出版年:起止页码.

(4) 期刊论文:作者(姓在前).论文题名[J].期刊名,年,卷(期):起止页码.

(5) 论文集中的析出文献:作者(姓在前).论文题名[C]//论文集责任者．论文集名.出版地:出版社,出版年.

(6) 学位论文:作者(姓在前).学位论文题目[D].收藏地:收藏单位,答辩年份.

(7) 电子文献:作者(姓在前).题名[EB/OL].出版地:出版社,出版年[引用日期].获取或访问路径.

4 来稿经审查后,编辑部有权对来稿作适当文字修改.来稿不退,请作者自留底稿.稿件刊登后,赠送该期刊2册.作者如需改投它刊,可通知本刊编辑部.

5 本刊不刊登已发表过的文章,请勿一稿多投.

6 本刊采用网上投稿,敬请关注本刊网站(http://puremathe.paperonce.org/).

Gorenstein fp-flat and strongly Gorenstein fp- fl at modules

Chen Wenjing
(College of Mathematics and Statistics,Northwest Normal University,Lanzhou730070,China)

The notions of Gorenstein fp- fl at and strongly Gorenstein fp- fl at modules are introduced,and the properties,connections as well as stability of two classes of these modules are discussed.

Gorenstein fp- fl at module,strongly Gorenstein fp- fl at module,projectively resolving

O153.3

A

1008-5513(2014)03-0323-08

10.3969/j.issn.1008-5513.2014.03.015

2013-11-17.

国家自然科学基金(11261050).

陈文静(1989-),硕士生,研究方向：同调代数.