3维幂零李超代数的Yang-Baxter算子

顾金剑,刘文德

(哈尔滨师范大学数学系,黑龙江哈尔滨150025)

3维幂零李超代数的Yang-Baxter算子

顾金剑,刘文德

(哈尔滨师范大学数学系,黑龙江哈尔滨150025)

在复数域C上,利用3维幂零李超代数的分类,通过计算刻画了3维幂零李超代数的Yang-Baxter算子.

Yang-Baxter算子;幂零李超代数;Yang-Baxter方程

1 引言

Baxter于1960年提出Baxter算子的概念[1].Rota在60年代初给出了很多Baxter算子的例子[2],并提出Rota-Baxter算子的概念.无论在数学还是物理领域,Rota-Baxter算子都被广泛的应用,如:Yang-Baxter方程[3]、量子场理论[4-5].物理学家在80年代发现了经典Yang-Baxter关系与Baxter代数的关系.文献[6]系统的研究了经典Yang-Baxter方程,发现了经典Yang-Baxter方程与左对称代数有密切关系,证明了Yang-Baxter算子可以用线性映射表示,并且此线性映射满足与Rota-Baxter算子相似的等式.文献[7]表明Rota-Baxter关系不仅仅对结合代数成立,对李代数和pre-李代数依然成立.Rota在90年代推进了关于Baxter算子方面的研究.从20世纪80年代起,Yang-Baxter系统一直是数学和物理领域最重要的研究课题之一.文献[8]刻画了(G,Θ)李代数的Yang-Baxter算子,文献[9]证明了Yang-Baxter算子与Hom-李代数有密切关系,但很少有关于李超代数Yang-Baxter算子具体形式的研究.

李超代数是非常重要的研究领域,而幂零李超代数在李超代数中占有重要地位.事实上,计算出幂零李超代数的Yang-Baxter算子是一项十分有意义的工作.虽然一般幂零李超代数的分类还没有实现,但是利用低维幂零李超代数的分类定理可以计算出某些低维幂零李超代数的所有Yang-Baxter算子,从而为计算高维幂零李超代数的Yang-Baxter算子提供参考.

本文利用3维幂零李超代数在同构意义下的分类[10],刻画了复数域上3维幂零李超代数的所有Yang-Baxter算子.

2 基本概念和引理

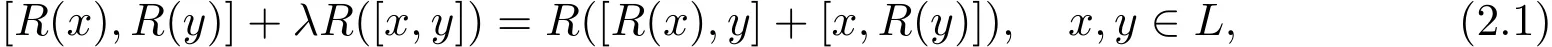
Abel李超代数是特殊的幂零李代数,由于Abel李超代数的任意线性变换均为Yang-Baxter算子,所以本文只考虑非Abel幂零李超代数的Yang-Baxter算子.

下面列出非Abel幂零李超代数在同构意义下的分类:

引理2.1[10]C上的任意3维非Abel幂零李超代数必同构于如下3类李超代数之一:

(1)L3,1,它具有一个基{a|α,β},基元素之间的非零李乘如下:[a,β]=α;

(2)L3,2,它具有一个基{a|α,β},基元素之间的非零李乘如下:[α,α]=a,[β,β]=a;

(3)L3,3,它具有一个基{a|α,β},基元素之间的非零李乘如下:[α,α]=a,[β,β]=−a.

令{x1,...,xn}是L的一组固定基,并设

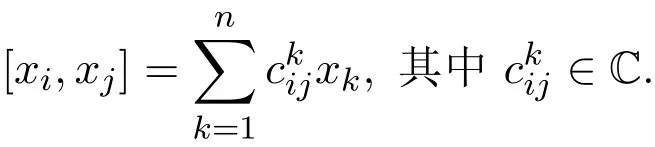
以下将L上的Yang-Baxter算子R写成矩阵(rij)形式,其中(rij)由等式唯一确定.

注记2.1当i=0时,Rij简记为Rj.

3 幂零李超代数的Yang-Baxter算子

引理3.1幂零李超代数L3,1的权为0的Yang-Baxter算子有6种,分别是Rij,其中i=0,j=1,………,6;幂零李超代数L3,1的权为1的Yang-Baxter算子有8种,分别是Rij,其中,当i=0时,j=7,………,9;当i=1时,j=0,………,4(Rij的具体形式见证明).

证明利用L3,1的乘法表分四种情况计算:

(1)当λ=0且R是奇线性映射时,有

于是,R满足(2.1)式,当且仅当,r21=0,r13r31=0,所以L3,1的权为0的奇Yang-Baxter算子为:

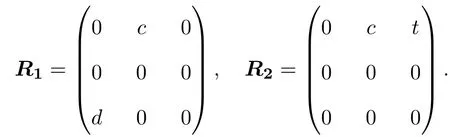
(2)当λ=0且R是偶线性映射时,有

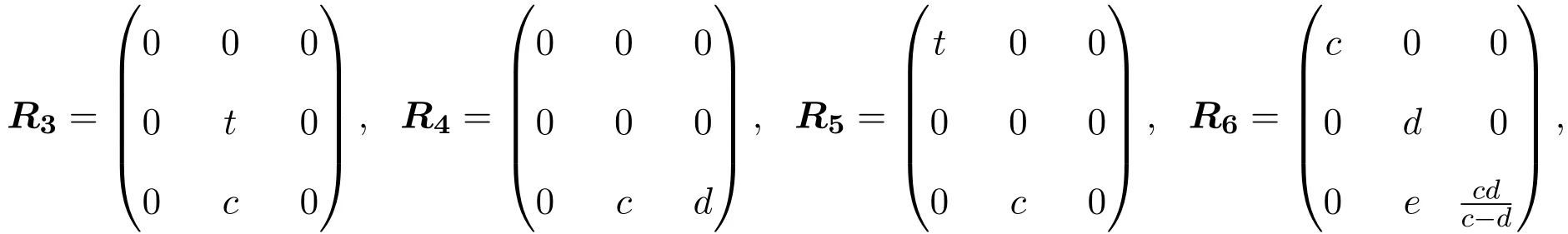
其中c/=d.

(3)当λ=1且R是奇线性映射时,有(3.1)-(3.3)式成立,于是,R满足(2.1)式,当且仅当r21=0,r13r31=0.此时的Yang-Baxter算子具有的矩阵形式与L3,1的权为0的奇Yang-Baxter算子相同,所以L3,1的权为1的Yang-Baxter算子为:R7=R1,R8=R2.

(4)当λ=1且R是偶线性映射时,有(3.4)-(3.6)式成立,于是,R满足(2.1)式,当且仅当r23=0,r11r33+r22−r22(r33+r11)=0,所以L3,1的权为1的偶Yang-Baxter算子为:

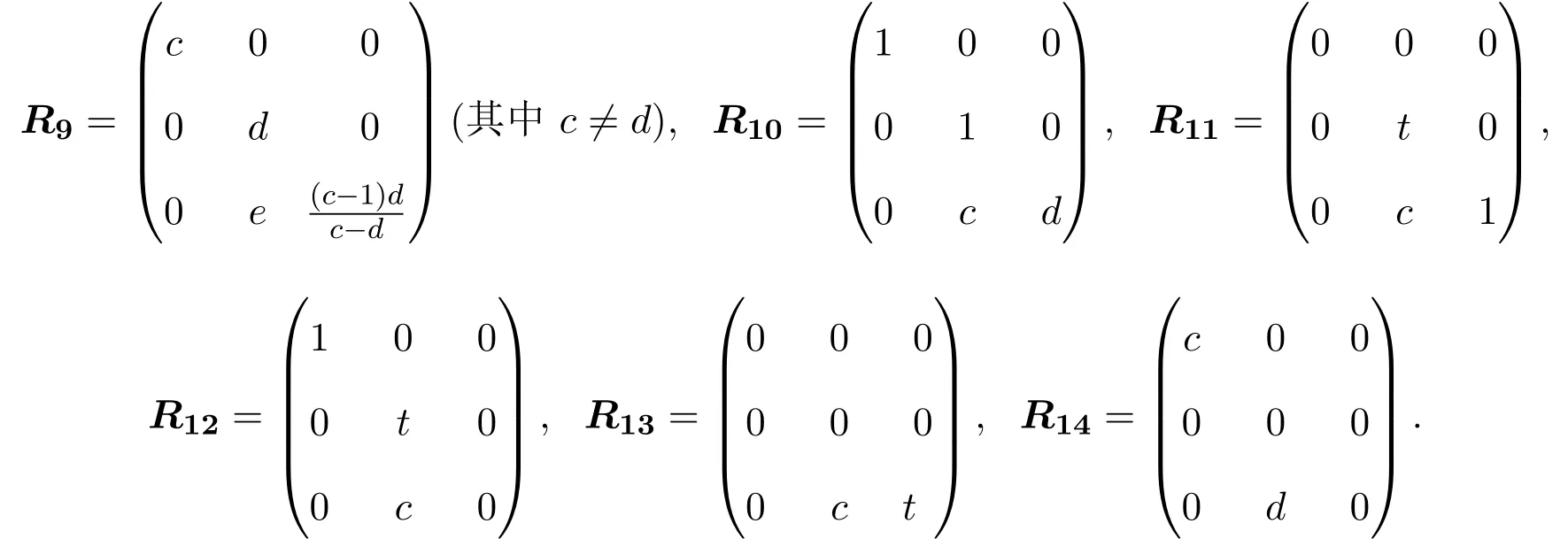
引理3.2幂零李超代数L3,2的权为0的Yang-Baxter算子有6种,分别是Rij,其中,当i=1时,j=5,………,9;当i=2时,j=0;幂零李超代数L3,2的权为1的Yang-Baxter算子有13种,分别是Rij,其中,当i=2时,j=1,………,9;当i=3时,j=0,………,3(Rij的具体形式见证明).

证明利用L3,2的乘法表分四种情况计算:

(1)当λ=0且R是奇线性映射时,有(3.1)-(3.3)式成立,于是,R满足(2.1)式,当且仅当r12=r13=0,所以L3,2的权为0的奇Yang-Baxter算子为:

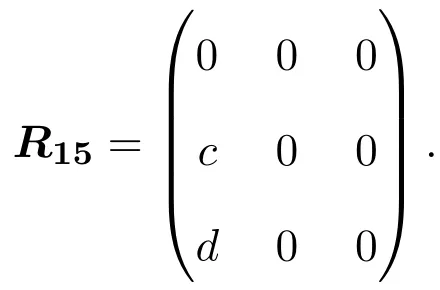
(2)当λ=0且R是偶线性映射时,有(3.4)-(3.6)式成立,于是,R满足(2.1)式,当且仅当

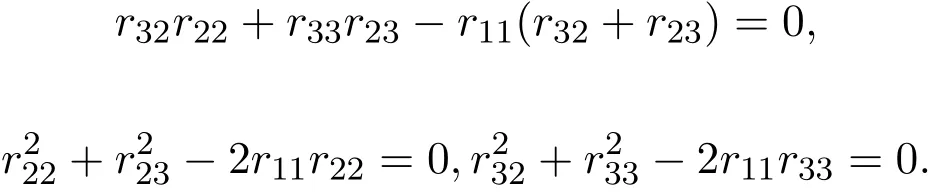
所以L3,2的权为0的偶Yang-Baxter算子为:

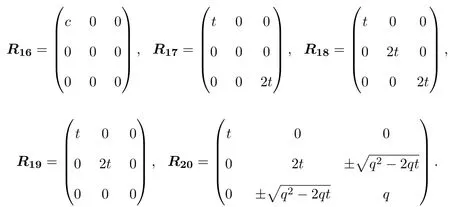
(3)当λ=1且R是奇线性映射时,有(3.1)-(3.3)式成立,于是,R满足(2.1)式,当且仅当r12=r13=0.此时Yang-Baxter算子具有的矩阵形式与L3,2的权为0的奇Yang-Baxter算子相同,所以L3,2的权为1的奇Yang-Baxter算子为:R21=R15.

(4)当λ=1且R是偶线性映射时,有(3.4)-(3.6)式成立,于是,R满足(2.1)式,当且仅当

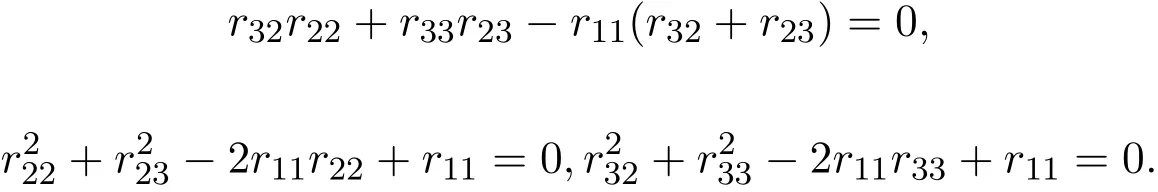
此时Yang-Baxter算子具有的矩阵形式与L3,2的权为0的偶Yang-Baxter算子相同,所以L3,2的权为1的偶Yang-Baxter算子为:

引理3.3幂零李超代数L3,3的权为0的Yang-Baxter算子有9种,分别是Rij,其中,当i=3时,j=4,………,9;当i=4时,j=0,………,2;幂零李超代数L3,3的权为1的Yang-Baxter算子有18种,分别是Rij,其中,当i=4时,j=3,………,9;当i=5时,j=0,………,9;当i=6时,j=0(Rij的具体形式见证明).

证明利用L3,3的乘法表分四种情况计算:

(1)当λ=0且R是奇线性映射时,有(3.1)-(3.3)式均成立,于是,R满足(2.1)式,当且仅当r12=r13=0.所以L3,3的权为0的奇Yang-Baxter算子为:R34=R15.

(2)当λ=0且R是偶线性映射时,有(3.4)-(3.6)式成立,于是,R满足(2.1)式,当且仅当

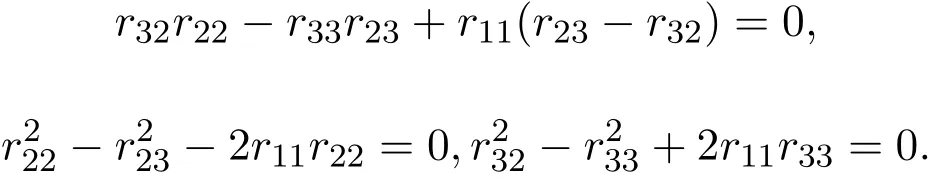
所以L3,3的权为0的偶Yang-Baxter算子为:

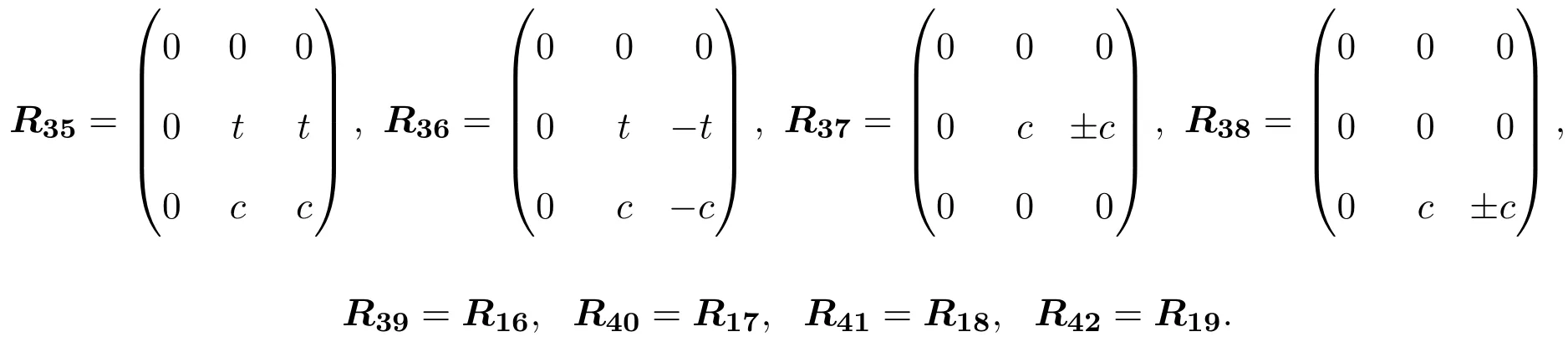
(3)当λ=1且R是奇线性映射时,有(3.1)-(3.3)式成立,于是,R满足(2.1)式,当且仅当r12=r13=0.此时Yang-Baxter算子具有的矩阵形式与L3,3的权为0的奇Yang-Baxter算子相同,所以L3,3的权为1的奇Yang-Baxter算子为:R43=R15.

(4)当λ=1且R是偶线性映射时,有(3.4)-(3.6)式成立,于是,R满足(2.1)式,当且仅当

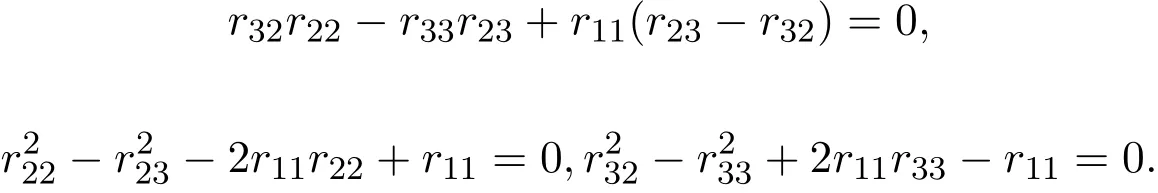
此时Yang-Baxter算子具有的矩阵形式与L3,3的权为0的偶Yang-Baxter算子相同,所以L3,3的权为1的偶Yang-Baxter算子为:

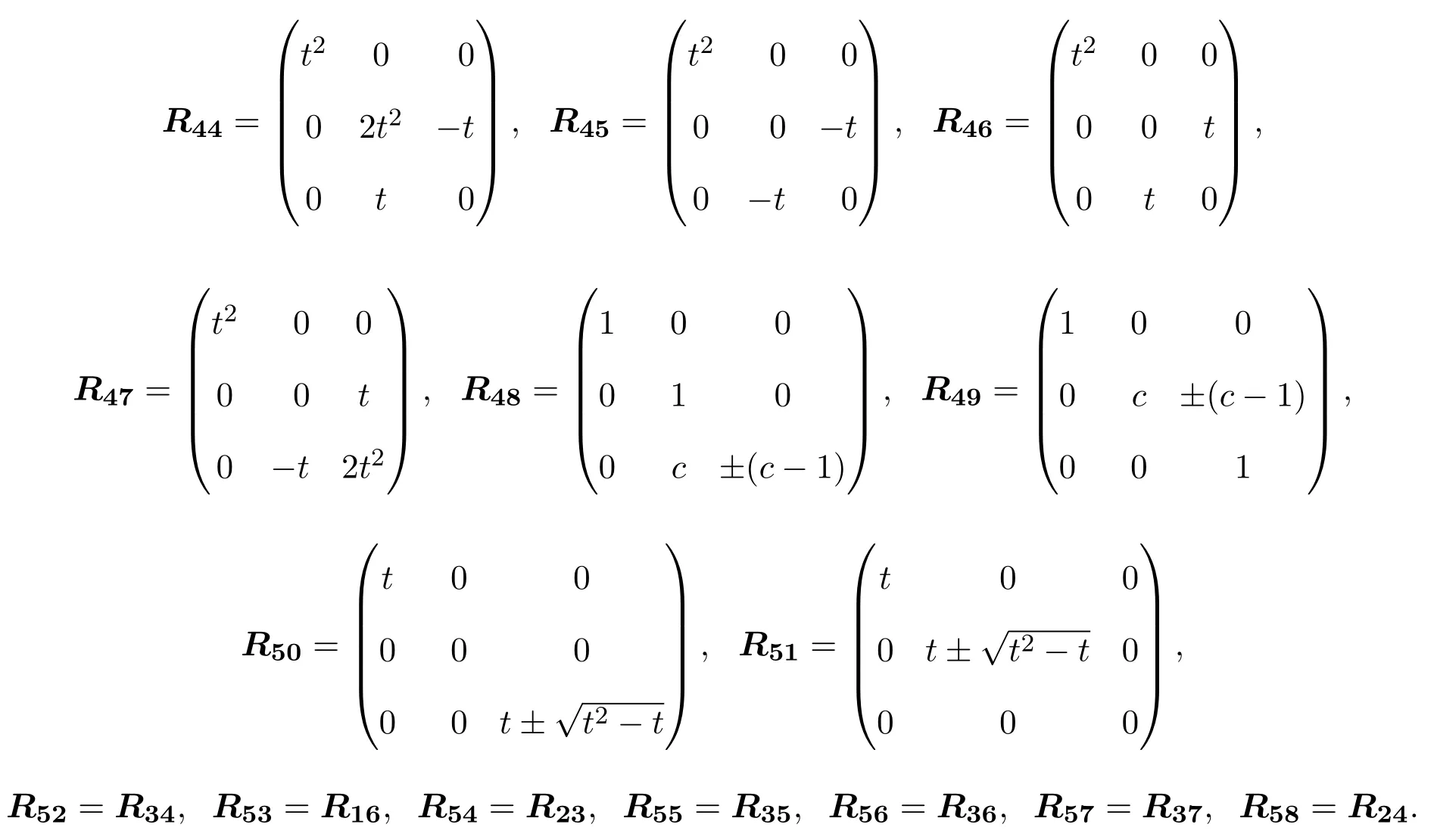
由引理3.1至引理3.3可以得出如下定理:

定理3.43维非Abel幂零李超代数L的Yang-Baxter算子Rij如表1所列:

表13维非Abel幂零李超代数L的Yang-Baxter算子Rij

其中,Rij的具体形式见引理3.1至引理3.3的证明.

[1]Baxter G.An analytic problem whose solution follows from a simple algebraic identity[J].Paci fi c J.Math., 1960,10(3):731-742.

[2]Rota G C,Smith D A.Fluctuation Theory and Baxter Algebras[C].Symposia Math.,1972,9:179-201.

[3]Aguiar M.On the associative analog of Lie bialgebras[J].J.Algebra,2001,244(2):492-532.

[4]Ebrahimi-Fard K,Guo L,Kreimer D.Spitzer′s identity and the algebraic Birkho ffdecompositon in pQFT[J]. J.Phys.A:Math.Gen.,2004,37(45):11037-11052.

[5]Connes A,Kreimer D.Hopf Algebras,Renormalization and Noncommutative Geometry[M].Netherlands: Springer,1999.

[6]Bai C.A uni fi ed algebraic approach to the classical Yang-Baxter equation[J].J.Phys.A:Math.Theory, 2007,40(36):11073-11082.

[7]Ebrahimi-Fard K,Guo L,Kreimer D.Integrable renormalization I:the ladder case[J].J.Math.Phys., 2004,45:3758-3769.

[8]Nichita F F.Lie algebras and Yang-Baxter equations[J].arXiv:1107.0920v1.

[9]Yau Donald.The Hom-Yang-Baxter equation and Hom-Lie algebras[J].J.Math.Phys.,2011,52(5):3502-3520.

[10]Backhouse Nigel.A classi fi cation of four dimensional Lie superalgebras[J].J.Math.Phys.,1978,19(11):2400-2402.

Yang-Baxter operators on the Lie superalgebras of dimension three

Gu Jinjian,Liu Wende
(School of Mathematical Sciences,Harbin Normal University,Harbin150025,China)

Let C be a complex fi eld.In this paper,employing the classi fi cation of Lie superalgebras of dimension 3,we fi nd out all the Yang-Baxter operators on the nilpotent Lie superalgebras of dimensions 3.

Yang-Baxter operators,Nilpotent Lie superalgebras,Yang-Baxter equation

O152.5

A

1008-5513(2014)03-0307-07

10.3969/j.issn.1008-5513.2014.03.013

2014-01-18.

黑龙江省教育厅科学研究基金(12511349);国家自然科学基金(11171055);黑龙江省杰出青年基金(JC201004).

顾金剑(1989-),硕士生,研究方向：李代数与李超代数.

刘文德(1965-),博士,教授,博士生导师,研究方向：李代数与李超代数.

2010 MSC:17B20,17B40,17B50