两类图的符号控制数

任媛,赵凌琪,吉日木图,王妍

(1.内蒙古民族大学数学学院,内蒙古通辽市028043; 2.内蒙古民族大学计算机科学与技术学院，内蒙古通辽市028043; 3.山东水利职业学院信息工程系,山东日照276826)

两类图的符号控制数

任媛1,赵凌琪2,吉日木图1,王妍3

(1.内蒙古民族大学数学学院,内蒙古通辽市028043; 2.内蒙古民族大学计算机科学与技术学院，内蒙古通辽市028043; 3.山东水利职业学院信息工程系,山东日照276826)

图G的符号控制数(G)有着许多重要的应用背景,因而确定其精确值有重要意义.Cm表示m个顶点的圈,n−Cm和n…Cm分别表示恰有一条公共边或一个公共顶点的n个Cm的拷贝.给出了n−Cm和n…Cm的符号控制数.

图;符号控制函数;符号控制数

1 引言

本文中所指的图均为无向简单图,文中未说明的符号和术语同文献[1].

近些年来,图的控制理论的研究越来越广泛,各种控制概念相继产生,例如符号边控制,符号边全控制,减控制,弱符号控制,符号星K控制等等,并获得了一些初步的研究成果[2-6],尤其是对图的符号控制,得到了许多新的结论[7-11].设图G=(V,E).v∈V,v的开邻域是与v相邻接的顶点集合,即N(v)={u|uv∈E}.称N(v)∪{v}为v的闭邻域,记为N[v].

定义1.1[7]图G=(V,E)的顶点集V上,定义一个双值函数f:V→{−1,+1},并且f[v]=f(N[v]),若在任何一个顶点v的闭邻域N[v]上函数值的和至少是1,即∀v∈V, f(N[v])≥1,则称函数f是G的一个符号控制函数.一个符号控制函数的权重是

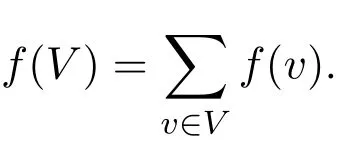
图G的符号控制数γs(G)定义为γs(G)=min{f(V)|f是G的符号控制函数}.

定理1.1[7]对阶为n≥3的圈图

定理1.2[7]对完全图Kn,有

定理1.3[7]星图K1,m的符号控制数γs(K1,m)=m+1.

对二部图Km,n(n≥m≥2),有下面两个定理:

定理1.4[7]当m=2,3时,有

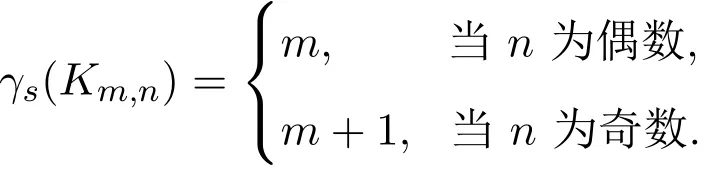
定理1.5[7]当n≥m≥4时,有

定理1.6[8]对任意正整数n≥2,扇图

定理1.7[8]对任意正整数n≥3,轮图

定理1.8[9]对于任意n阶图G,∆和δ分别为图G的最大度和最小度,则有

本文给出了n−Cm和n…Cm的符号控制数.

2 主要结果

定理2.1对任意正整数m≥3,n≥2,有

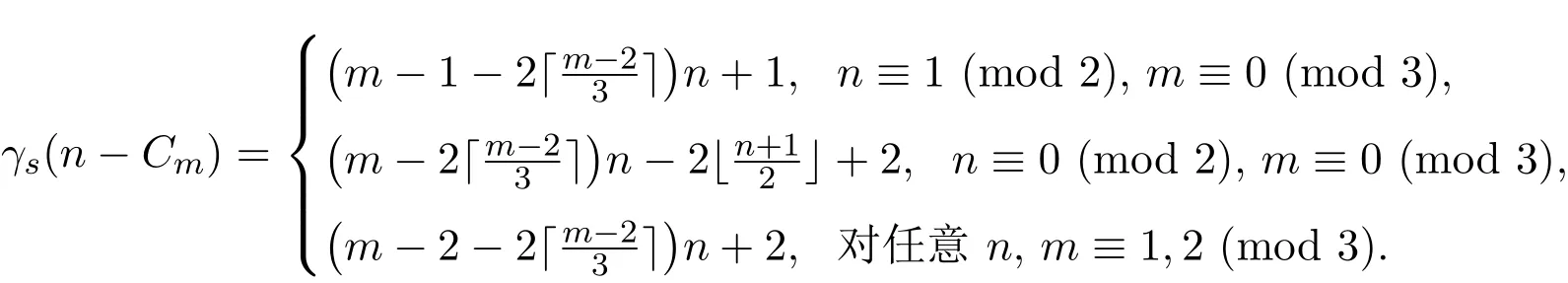
证明令表示n−Cm中的第i个m-圈,u和v表示的两个公共顶点,n−Cm中的第i个m-圈中余下的顶点依次为

设函数f是n−Cm的一个符号控制函数,注意到:

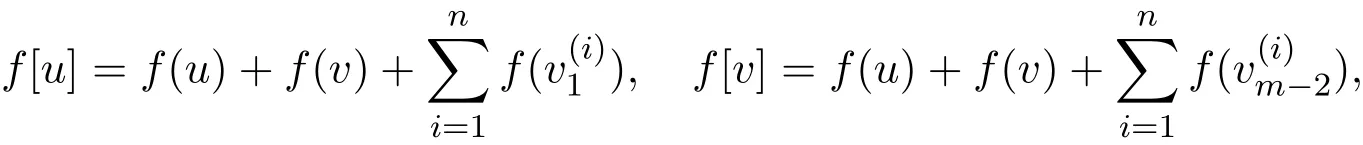
下面分三种情况进行讨论.

情况1当m≡0(mod 3)时,考虑u和v的对称性,只需讨论下面三种情况.

情况1.1当f(u)=f(v)=−1时.

当m=3时,不满足符号控制函数的定义,故下面考虑m>3时,由

容易得到每个m-圈中余下(m−6)个顶点中分配值为−1的个数最多为现在考虑每个m-圈中余下(m−6)个顶点中分配值为−1的个数为时,下面给出此时的一个符号控制函数:

情况1.2当f(u)=−1,f(v)=+1时.

容易得到每个m-圈中余下(m−4)个顶点中分配值为−1的个数最多为现在考虑每个m-圈中余下(m−4)个顶点中分配值为−1的个数为时,下面给出此时的一个符号控制函数:

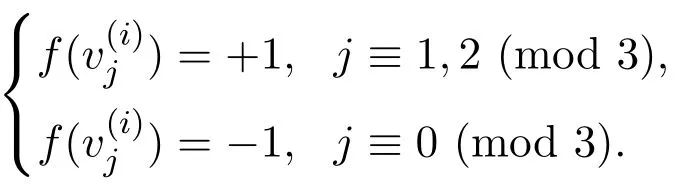
情况1.3当f(u)=f(v)=+1时.

下面讨论n−Cm(m≡0(mod 3))中满足上述条件的的个数:

由

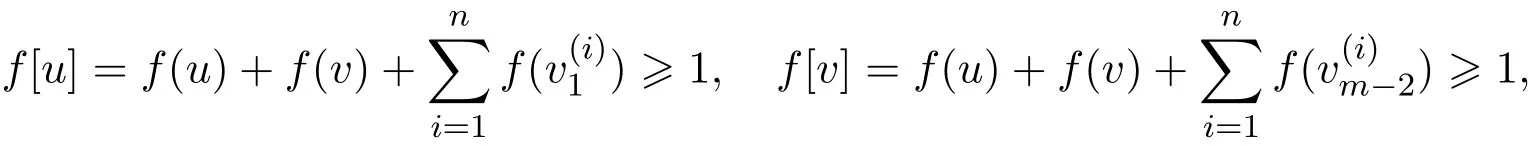
此时,f是满足要求的、权最小的一个符号控制函数.

情况1.3.1当n≡1(mod 2)时,此时

情况1.3.2当n≡0(mod 2)时,此时

结合情况1.1,情况1.2,情况1.3,有

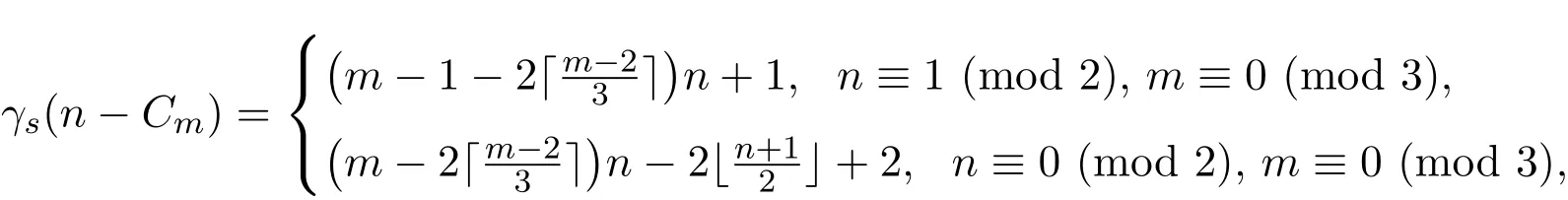
其中m≡0(mod 3).

情况2当m≡1(mod 3)时,考虑u和v的对称性,只需讨论下面三种情况.

情况2.1当f(u)=f(v)=−1时.

用情况1.1中同样的方法,容易得到每个m-圈中余下(m−6)个顶点中分配值为−1的个数最多为现在考虑每个m-圈中余下(m−6)个顶点中分配值为−1的个数为时,下面给出此时的一个符号控制函数:

情况2.2当f(u)=−1,f(v)=+1时.

情况2.3当f(u)=f(v)=+1时.

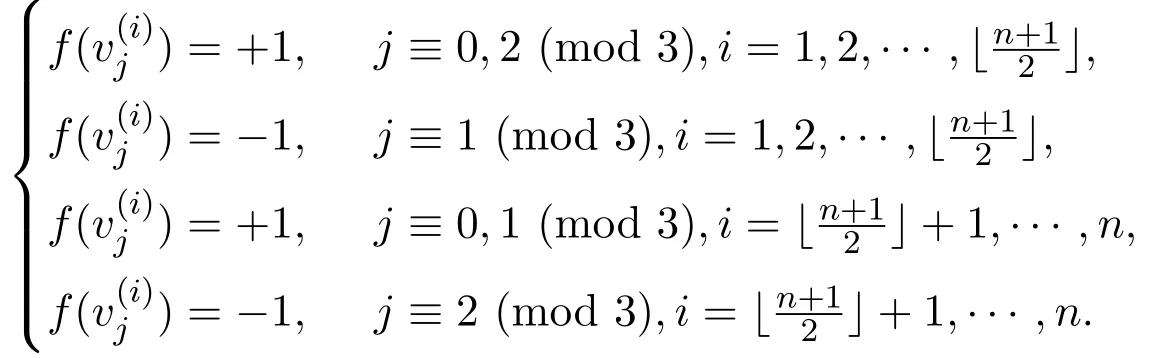
结合情况2.1,情况2.2,情况2.3,有

情况3当m≡2(mod 3)时,考虑u和v的对称性,只需讨论下面三种情况.

情况3.1当f(u)=f(v)=−1时.

情况3.2当f(u)=−1,f(v)=+1时.

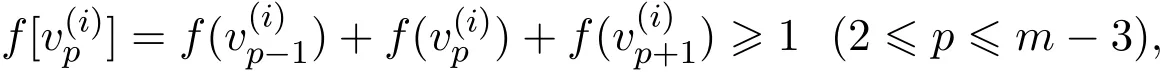
容易得到每个m-圈中余下(m−5)个顶点中分配值为−1的个数最多为现在考虑每个m-圈中余下(m−5)个顶点中分配值为−1的个数为时,又由

此时,f是满足要求的、权最小的一个符号控制函数.

情况3.2.1当n≡1(mod 2)时,此时

情况3.2.2当n≡0(mod 2)时,此时

情况3.3当f(u)=f(v)=+1时.

结合情况3.1,情况3.2,情况3.3,有

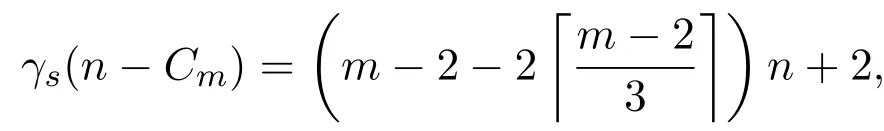
其中m≡2(mod 3).

综上所述,对任意正整数m≥3,n≥2,

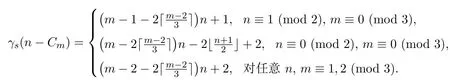
定理2.2对任意正整数m≥3,n≥2,

证明令表示n…Cm中的第i个m-圈,u表示的公共顶点,n…Cm中的第i个m-圈中余下的顶点依次为

设函数f是n…Cm的一个符号控制函数,注意到:

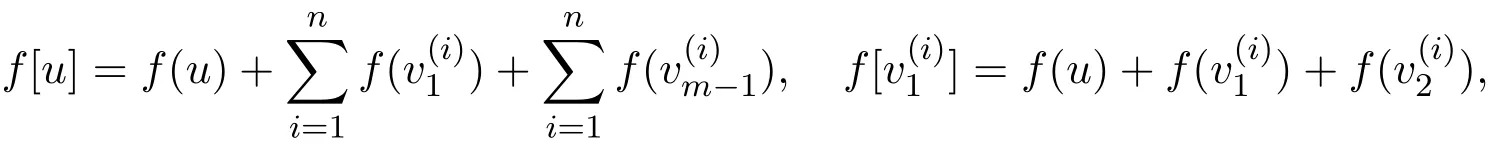
下面分三种情况进行讨论:

情况1当m≡0(mod 3)时.

下面给出此时的一个符号控制函数:

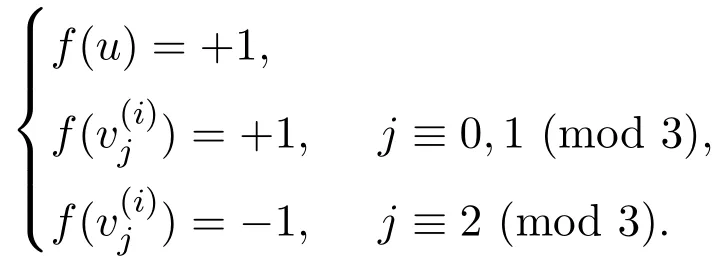
情况2当m≡1(mod 3)时.

情况2.1当f(u)=−1时.

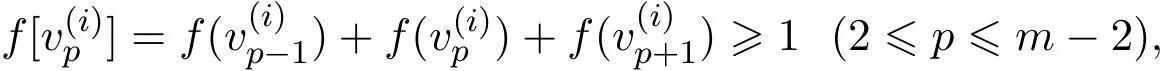
容易得到每个m-圈中余下(m−5)个顶点中分配值为−1的个数最多为现在考虑每个m-圈中余下(m−5)个顶点中分配值为−1的个数为时,下面给出此时的一个符号控制函数:

情况2.2当f(u)=+1时.

由容易得到每个m-圈中余下(m−1)个顶点中分配值为−1的个数最多为现在考虑每个m-圈中余下(m−1)个顶点中分配值为−1的个数为时,下面给出此时的一个符号控制函数:

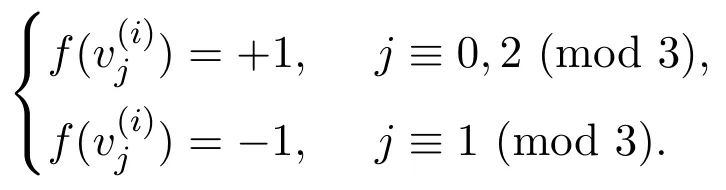
结合情况2.1,情况2.2,有

情况3当m≡2(mod 3)时.

情况3.1当f(u)=−1时.

情况3.2当f(u)=+1时.

下面讨论n…Cm(m≡2(mod 3))中满足上述条件的的个数:

由

此时,f是满足要求的、权最小的一个符号控制函数.

情况3.2.1当n≡1(mod 2)时,此时

情况3.2.2当n≡0(mod 2)时,此时

结合情况3.1,情况3.2,有

综上所述,对任意正整数m≥3,n≥2,

[1]Bondy J A,Murty U S R.Graph Theory With Applications[M].London:Macmillan,1977.

[2]Xu Baogen.On signed edge domination numbers of graphs[J].Discrete Math.,2001,239:179-189.

[3]Zhao Jinfeng,Xu Baogen.On signed edge total domination numbers of graphs[J].Journal of Mathematical Research Exposition,2011,31(2):209-214.

[4]Xu Baogen.On minus domination and signed domination in graphs[J].J.Math.Res.Exposition, 2003,23(4):586-590.

[5]尚华辉,苗连英,苗正科,等.关于图的弱符号控制数的下界[J].纯粹数学与应用数学,2010,26(4):691-695.

[6]李春华.图的符号星K控制数[J].纯粹数学与应用数学,2009,25(4):638-641.

[7]于崇智,徐保根.图的符号控制数[J].华东交通大学学报,1997,14(4):54-58,67.

[8]于崇智.图的最小符号控制函数的充要条件[J].阴山学刊,1999,15(1):5-8.

[9]徐保根,丁宗鹏,罗茜.图的符号控制数的下界[J].华东交通大学学报,2011,28(3):69-72.

[10]王军秀.特殊图类的符号控制数[J].纯粹数学与应用数学,2005,21(1):59-61.

[11]徐保根.图的控制理论[M].北京:科学出版社,2008.

Signed domination numbers for two class of graphs

Ren Yuan1,Zhao Lingqi2,Jirimutu1,Wang Yan3
(1.College of Mathematics,Inner Mongolia University for Nationalities,Tongliao028043,China; 2.College of Computer and Technology,Inner Mongolia University for Nationalities,Tongliao028043,China; 3.Department of Information Engineering,Shandong Water Polytechnic,Rizhao276826,China)

The signed domination number of a graph has its import and applying background,so it is useful to determinate the exact value of it.Cmdenotes the cycle of length m,n−Cmand n…Cmdenote the graph obtained from any n copies of Cmwhich have just one common edge and one common vertex,respectively.In this paper,we obtain the signed domination numbers of n−Cmand n…Cm.

graph,signed domination function,signed domination number

O157.5

A

1008-5513(2014)03-0271-09

10.3969/j.issn.1008-5513.2014.03.008

2012-06-07.

国家自然科学基金(61261025,61262018);内蒙古民族大学校级研究项目(NMD1104).

任媛(1987-),硕士,助教,研究方向：图论及其应用.

2010 MSC:05C78