一类单调算子的新不动点定理

王维娜,薛西锋

(西北大学数学学院,陕西西安710127)

一类单调算子的新不动点定理

王维娜,薛西锋

(西北大学数学学院,陕西西安710127)

利用单调迭代法、数学归纳法以及序差距的性质,在半序Banach空间中探究不具有紧性、连续性以及任何凹凸性的单调算子不动点存在以及惟一性问题,得出其新不动点定理,这些结果对相关结论进行了推广,使其适用范围更广,同时将该结论应用于求解Volterra型积分方程组问题中.

单调算子;正规锥;不动点;序差对;序差距

1 引言及预备知识

对于单调算子不动点的研究,现已有许多的结果[1-8].有些文献在研究单调算子不动点时,要求单调算子具有某种紧性或连续性或凹凸性,文献[1]利用序差的性质及数学归纳法,文献[2-7]运用锥理论知识和单调迭代技巧,文献[8]采用与以往大不相同的假设和迭代格式均研究了不具有以上条件而满足其他某些条件的单调算子的不动点存在惟一性问题.本文在半序Banach空间中引入序差对和序差距的概念,利用单调迭代法、数学归纳法以及序差距的性质,去掉单调算子的紧性、连续性以及凹凸性,在更广泛的条件下,得到半序Banach空间中单调算子的新不动点定理,同时将其结论应用于求解Volterra型积分方程组的问题中,使其求解更加简便.

设E是Banach空间,P是E中的一个锥[3].

定义1.1锥P是正规的,若存在常数N>0,使得θ≤x≤y⇒∥x∥≤N∥y∥,且称满足条件的最小正数N为P的正规常数.

定义1.2P是E中的锥,θ≤u≤v,对于h∈P,若∃M>0,使得v≤Mh,则令

称a−b为u和v的h-序差,并且记dh(u,v)=a−b.

定义1.3设a−b,c−d分别为u和v,r和s的h-序差,即dh(u,v)=a−b,dh(r,s)=c−d,则(dh(u,v),dh(r,s))为序差对.

定义1.4称序差对(dh(u,v),dh(r,s))到(0,0)点的距离为序差距,并且记为

定义1.5设E是半序空间[3],在E×E中定义新的半序关系:若x1≤x2,y1≥y2,则记(x1,y1)≤(x2,y2).

引理1.1设E是Banach空间,P为E中一个锥,则E×E在定义1.5的半序下是半序空间.

证明(i)∀(x1,y1)∈E×E,都有x1≤x1,y1≥y1,即(x1,y1)≤(x1,y1).

(ii)若(x1,y1)≤(x2,y2),且(x2,y2)≤(x3,y3),则有

故有x1≤x3,y1≥y3,即(x1,y1)≤(x3,y3).

(iii)若(x1,y1)≤(x2,y2),且(x2,y2)≤(x1,y1),则有

故有x1=x2,y1=y2,即(x1,y1)=(x2,y2).

由(i),(ii),(iii)可知E×E在定义1.5的半序下是半序空间.

引理1.2设B,C:[u0,v0]→E均为增算子,令A(x,y)=(Bx,Cy),则A在≤下是增算子;若B,C:[u0,v0]→E均为减算子,则A(x,y)=(Bx,Cy)在≤是减算子.

证明对任意x1,x2,y1,y2∈[u0,v0],若(x1,y1)≤(x2,y2),即x1≤x2,y1≥y2,又因为B,C为增算子,所以Bx1≤Bx2,Cy1≥Cy2,故有

则A为增算子.

若B,C均为减算子,当(x1,y1)≤(x2,y2)时,有Bx2≤Bx1,Cy2≥Cy1,即

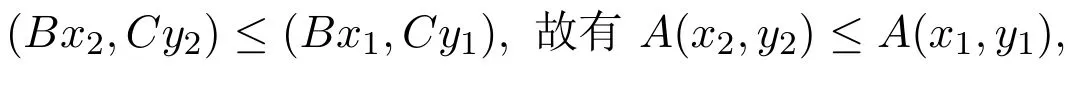
则A为减算子.

2 主要结果

定理2.1设P是E中的锥,θ≤u≤v,θ≤r≤s,h∈P,且∃M,L>0,使得v≤Mh, s≤Lh,那么,

(i)

(ii)d(dh(u,v),dh(r,s))=0,则u=v,r=s.

(iii)若θ≤u1≤u≤v,θ≤r1≤r≤s,则

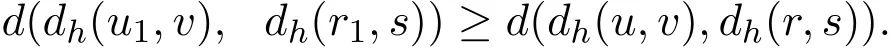
(iv)

证明(i)因为dh(u,v)≥0,dh(r,s)≥0,所以

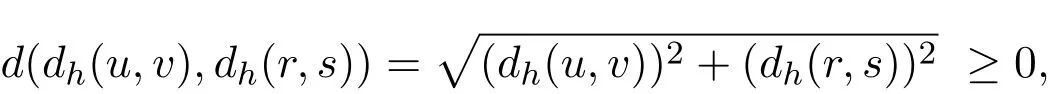
又因为dv(u,v)≤1,ds(r,s)≤1,所以

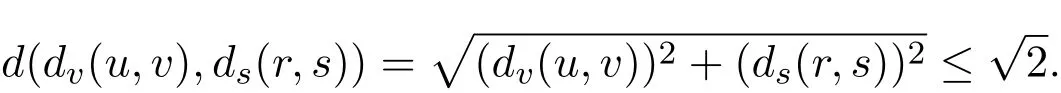
(ii)因为

要使等式成立,需满足dh(u,v)=0,且dh(r,s)=0.又因为dh(u,v)=0,则u=v;dh(r,s)=0,则r=s,故有u=v,r=s.

(iii)因为当θ≤u1≤u≤v,θ≤r1≤r≤s时,有

所以

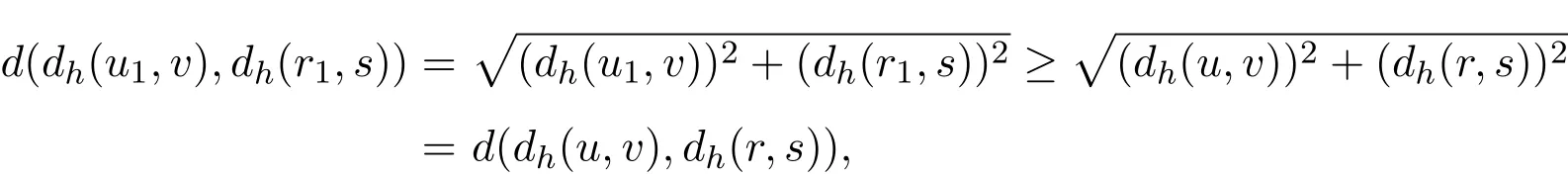
得证.

所以

又因为∀k∈[0,1],有dv(kv,v)=1−k,ds(ks,s)=1−k,所以

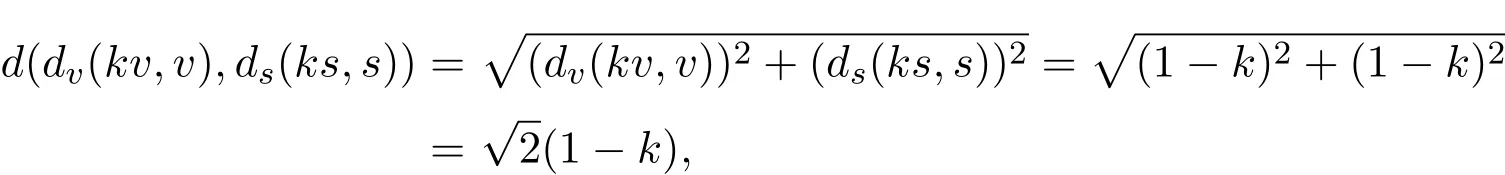
得证.

定理2.2设P是E中的正规锥,

为增算子,其中B,C:[u0,v0]→E均为增算子,且满足下列条件:

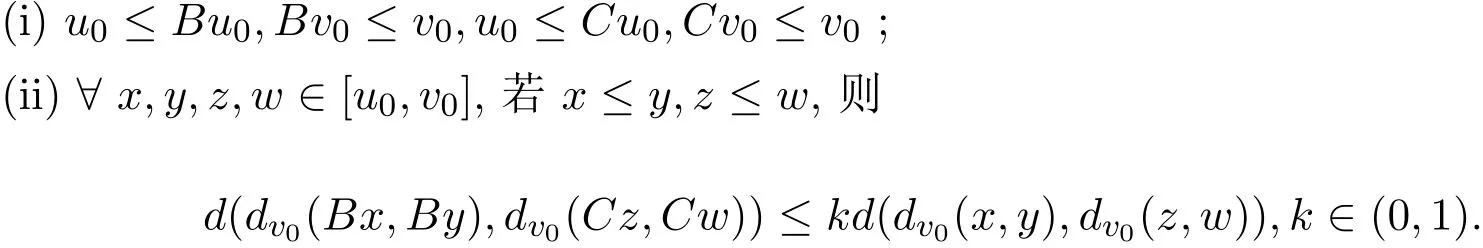
则A在[u0,v0]×[u0,v0]中有惟一不动点(x∗,y∗),且对任意的初值x0,y0∈[u0,v0],迭代序列xn=Bxn−1,yn=Cyn−1(n=1,2,………),必有xn→x∗,yn→y∗.

证明令

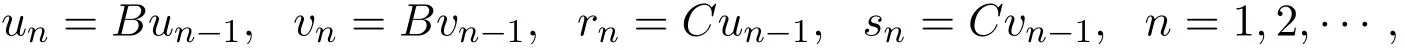
由条件(i),以及B,C是增算子可知,

由条件(ii),取k∈(0,1),可得

所以,当n→∞时,

即∀ε>0,∃N>0,使得当n>N时,有:

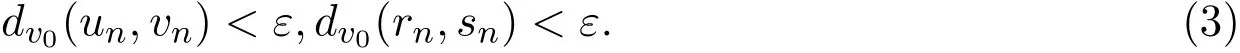
令

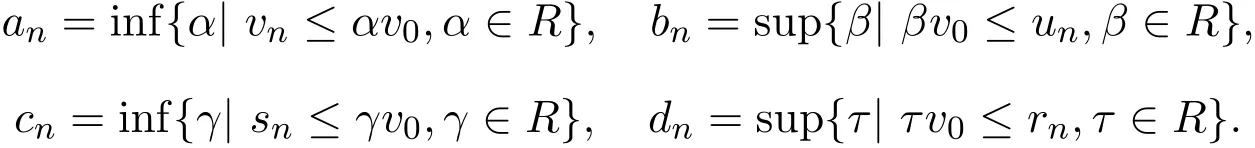
由(3)式可得:

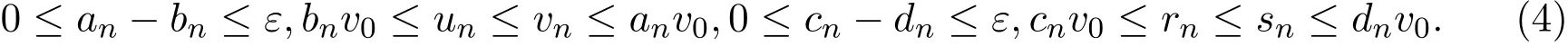
由P的正规性,以及(4)式可得:

所以

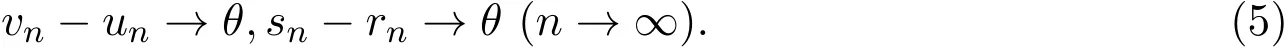
由(1)和(2)式可得:

由(2)和(6)式可知,

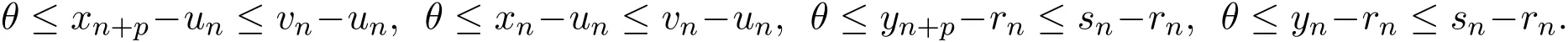
由P的正规性,以及(5)式得

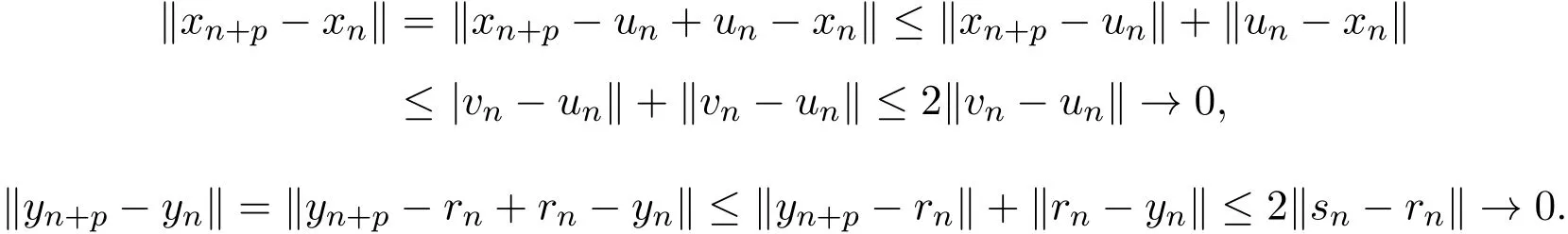
故{xn},{yn}都是Cauchy列.故存在(x∗,y∗)∈[u0,v0]×[u0,v0],使得

由(2)和(7)式可知,

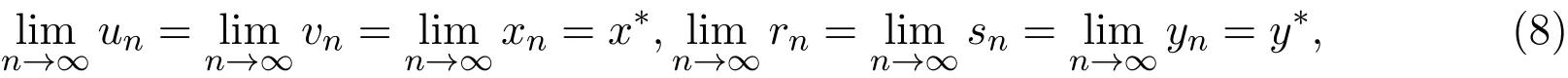
则

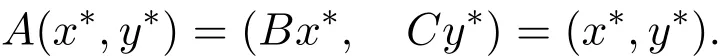
定理2.3设P是E中的正规锥,θ≤u0≤v0,A(x,y)=(Bx,Cy):[u0,v0]×[u0,v0]→E×E为减算子,其中B,C:[u0,v0]→E均为减算子,且满足下列条件:

(i)u0≤Bu0,Bv0≤v0,u0≤Cu0,Cv0≤v0;

(ii)∀x,y,z,w∈[u0,v0],若x≤y,z≤w,则

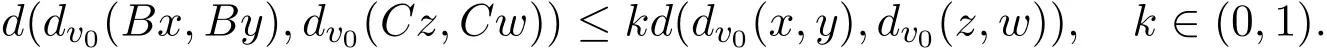
则A在[u0,v0]×[u0,v0]中有惟一不动点(x∗,y∗),且对任意的初值x0,y0∈[u0,v0],迭代序列xn=Bxn−1,yn=Cyn−1(n=1,2,………),必有xn→x∗,yn→y∗.

证明令H(x,y)=A2(x,y)=(B2x,C2y),易验证H:[u0,v0]×[u0,v0]→E×E为增算子,且

∀x,y,z,w∈[u0,v0],若x≤y,z≤w,由条件(ii)可知:

故定理2.2的条件(i),(ii)均满足,所以定理2.3的结论成立.

3 应用

研究Volterra型积分方程组解的问题:

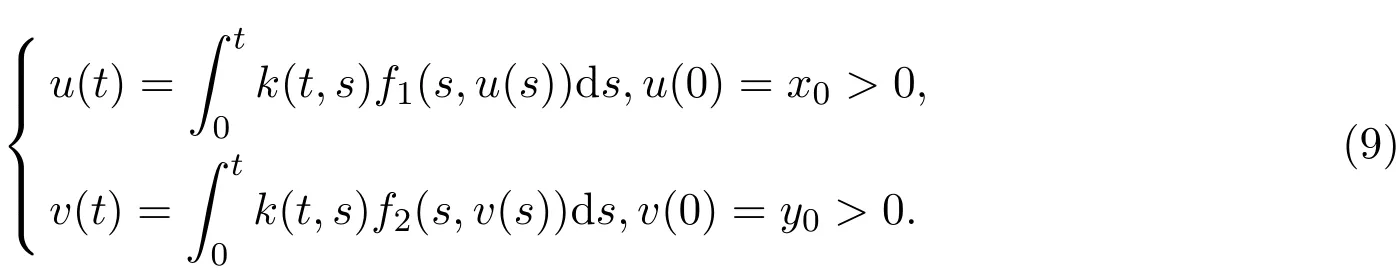
其中,k(t,s)在[0,1]×[0,1]上非负连续,f1(t,u),f2(t,v)在[0,1]×R上非负且分别关于u,v单调递增.设

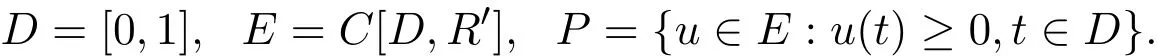
定理3.1在以上条件下,方程组解的问题(9)有惟一的恒正解:

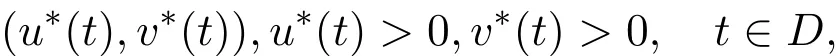
并且若(x0,y0)为初始点作迭代序列:

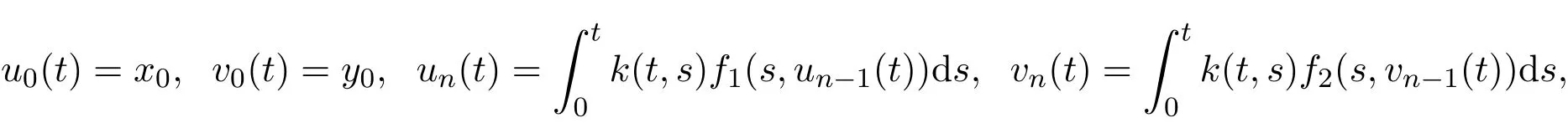
则(un(t),vn(t))在P×P上一致收敛于(u∗(t),v∗(t)).

证明∀(u,v)∈P×P,令

设A(u,v)(t)=(Bu(t),Cv(t)).由假设条件易知:P×P→E×E满足定理2.3的条件(i),(ii).则该定理的结论成立.

[1]栾辉.非紧非连续单调算子新不动点定理[J].南昌工程学院学报,2012,31(6):5-7.

[2]吴焱生.一类非紧非连续增算子新不动点定理及其应用[J].赣南师范学院学报,2004(6):14-16.

[3]孙经先.非线性泛函分析及应用[M].北京:科学出版社,2008.

[4]张金清,孙经先.一个非连续增算子不动点定理及其应用[J].应用数学学报,2001,24(1):34-43.

[5]Wu Y S,Li G Z.On the fi xed point existence and uniqueness theorems of mixed operators monotone operators and application[J].A.M.S.,2003,46(1):161-166.

[6]Hong S H.Fixed point for mixed monotone multivalued operators in Banach spaces with applications[J]. J.Math.Anal.Appl.,2008,337:333-342.

[7]郭大钧.非线性分析中的半序方法[M].济南:山东科学技术出版社,2000.

[8]颜苏平,王申林,黄翔.一类新型混合单调算子的不动点定理及在工程科技中的应用[J].纯粹数学与应用数学, 2010,26(3):403-408.

New fi xed point theorems of the monotone operator and its application

Wang Weina,Xue Xifeng
(School of Mathematics,Northwest University,Xi′an710127,China)

In order to explore the existence and uniqueness of monotone operator without compactness,continuity,and any convex conditions fi xed points in partially ordered Banach space,the paper uses the monotone iterative method and mathematical induction as well as the properties of the sequence gaps.Then we obtained the new fi xed point theorems of it.The results obtained generalize the related conclusion,so that it can be widely applicable scope,Meanwhile the conclusion is applied to solve the problem for Volterra integral equation group.

monotone operator,normal cone, fi xed point,order di ff erence pair,sequence gaps

O177.91

A

1008-5513(2014)03-0292-07

10.3969/j.issn.1008-5513.2014.03.011

2014-01-09.

陕西省自然科学基金(2012JM1017).

王维娜(1988-),硕士生,研究方向：非线性泛函分析.

2010 MSC:47H10