局部资料下变分同化方法的稳定性研究
2014-07-19张瑰
张瑰
(1.解放军理工大学理学院,江苏南京211101; 2.热带海洋环境国家重点实验室(中国科学院南海海洋研究所),广东广州510301)
局部资料下变分同化方法的稳定性研究
张瑰1,2
(1.解放军理工大学理学院,江苏南京211101; 2.热带海洋环境国家重点实验室(中国科学院南海海洋研究所),广东广州510301)
对于简化的一维扩散方程,在局部观测资料下,研究变分同化方法的稳定性.在变分同化中结合正则化方法,选择合适的正则化参数和稳定泛函,对预报模式进行修正,通过对预报精度进行先验估计,证明了该方法对于一维扩散方程的解的稳定性.修正补充相关计算结果,最后举出一个反例说明稳定性泛函的选取对于改进的变分同化方法实施的重要性.
局部资料;变分同化;正则化;稳定性;收敛精度
1 引言
现代气象科技的发展使天气预报能力和水平有了很大的提高,但是在常规气象探测技术和手段不能达到的海区和陆地,气象资料非常稀少或缺乏,这样会直接影响到天气、天候的分析研究和气象预报的准确性.因此研究如何利用有限的局部观测资料来提高预报精度,不仅具有的理论意义,而且具有重要的应用价值.
文献[1-2]讨论了局部观测资料下的变分同化问题,利用变分同化结合数学物理反问题中的正则化方法[3-4]对预报模式进行修正,分析了观测误差和模式误差对于变分同化方法的影响,结果表明:观测误差为ε时,在适当条件下,收敛精度达到同时,文献[5]以一维抛物型偏微分方程为例,考虑特定波解形式的初始条件,在局部观测资料下,利用变分方法通过确定最优的反演常数,证明收敛精度达到O(ε).文献[6]从部分数据信息出发给出了反演声波阻尼系数的一种新方法,利用Tikhonov正则化方法将问题转化为一个最优化问题,克服了第一类算子方程的不适定性所造成的困难,数值结果表明该方法是准确且简单易行的.文献[7]利用正则化反演法,对电离层层析成像技术进行了数值模拟,结果表明,正则化反演法能够得到很高精度的重建结果.
本文考虑一般形式的初始条件,在局部观测资料下,分析利用变分同化结合正则化方法的稳定性,得到解的收敛精度,进一步对文献[2]中相关计算结果进行修正、补充,证明在适当条件下,收敛精度为论文最后通过举出一个反例说明稳定性泛函对于改进变分同化方法的重要性,如果选取的稳定性泛函不合适,仍然不能保证解的稳定性.
2 模型的简化与问题的提出
对于一维扩散方程
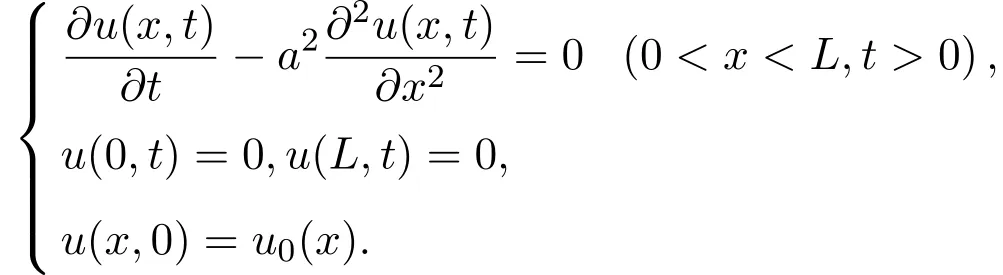
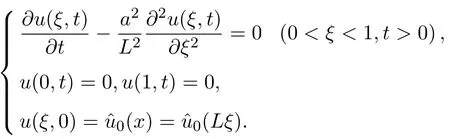
因此,为了理论研究上的方便,本文仅以简化的扩散方程[1-2]进行分析.
定义2.1精确解u(x,t)满足如下初边值问题:
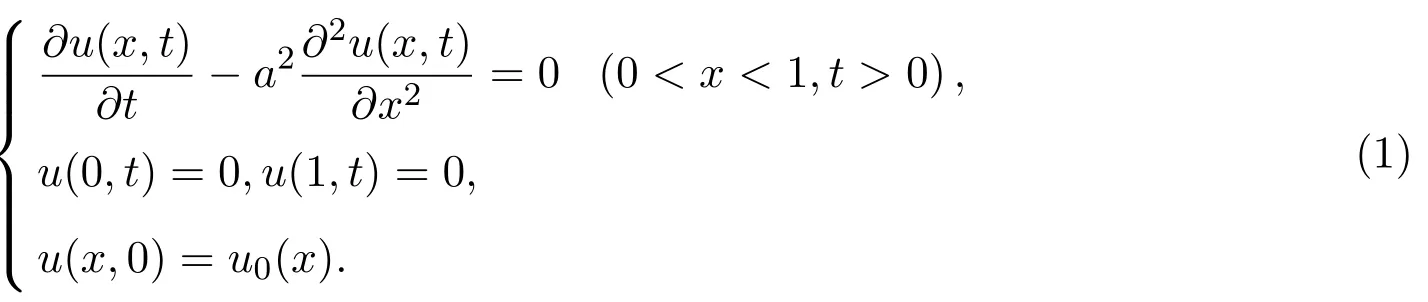
其中,系数a2>0为常数,u0(x)为真实初值.
假设t=t0处有局部观测资料gobs(x),观测资料带有误差:

其中
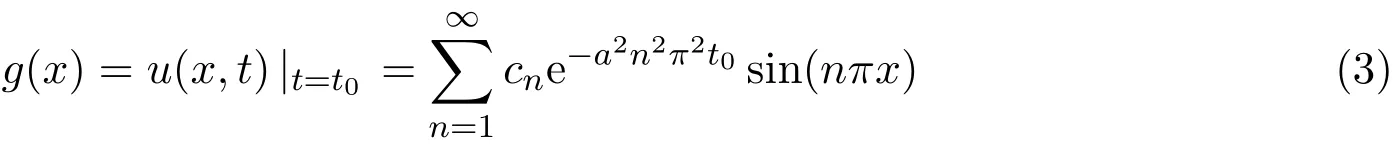
为t=t0处的精确值,g′(x)为观测误差函数.进一步假设g′(x)=εH(x),ε>0为观测误差的界,H(x)∈L2[0,1],且
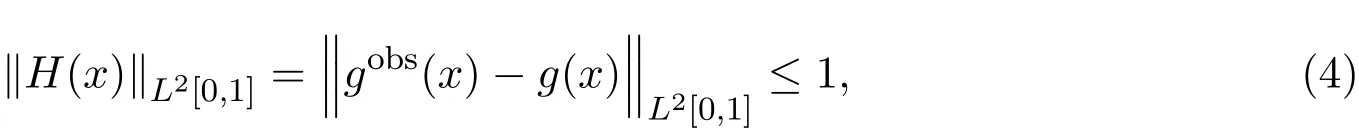
下面考虑一维扩散方程的反问题,即:假设(1)中的初值u0(x)未知,利用局部资料gobs(x)对初值进行最优确定.
3 通常变分同化方法的不适定性
定义3.1预报解(x,t)满足如下初边值问题:
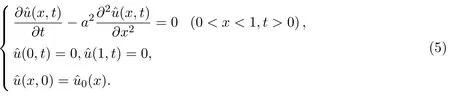
对初值进行反演,即在预报值与观测值之间建立极小模泛函:
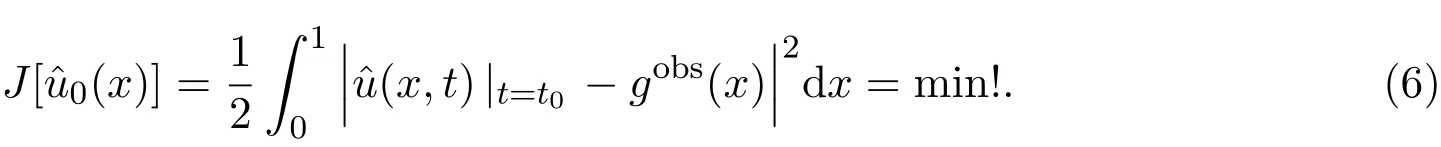
求解极值问题(6),得到初值为:
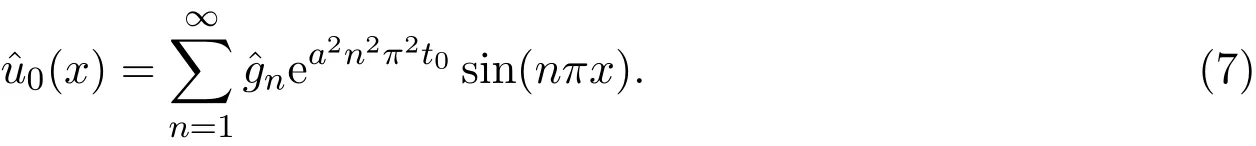
其中
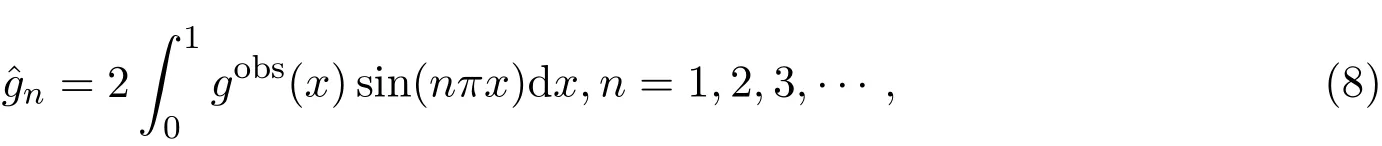
4 结合正则化的变分同化方法
利用Tikhonov正则化思想[3],引入稳定泛函及正则化参数[4,9],对通常的变分同化方法进行改进.
定义4.1改进后的目标泛函:
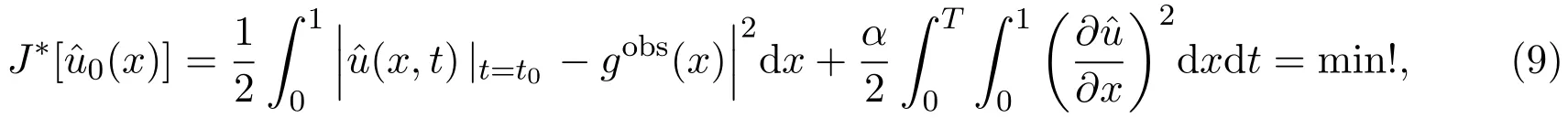
下面求解泛函极值问题(9).利用关系式

将问题转化为:
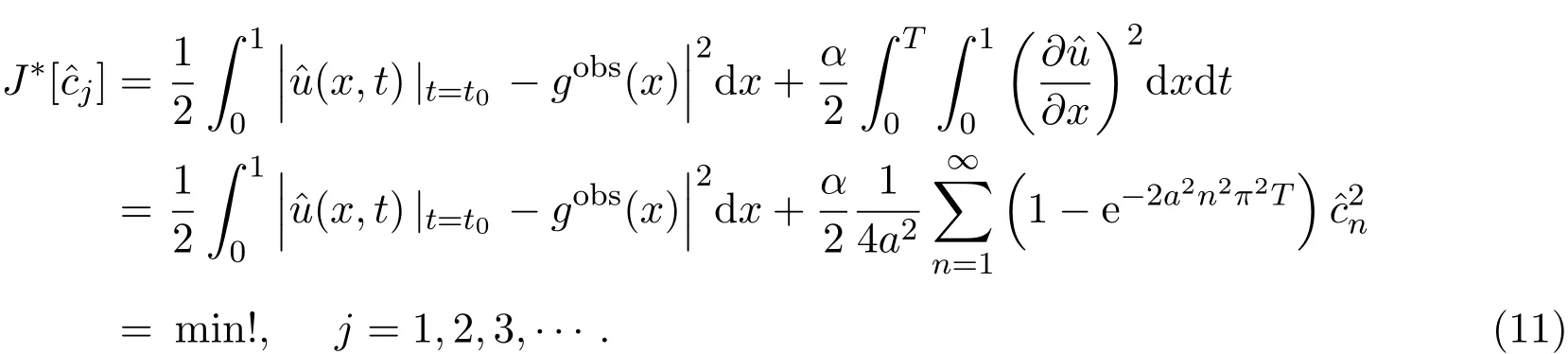
利用δJ∗=0和{sin(nπx)}的正交性计算得到:
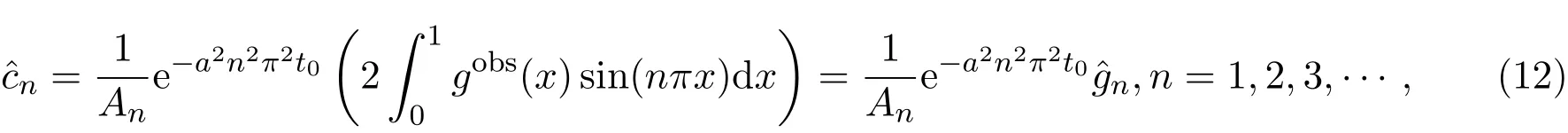
由(10)式和(12)式得到改进后的最优初值:
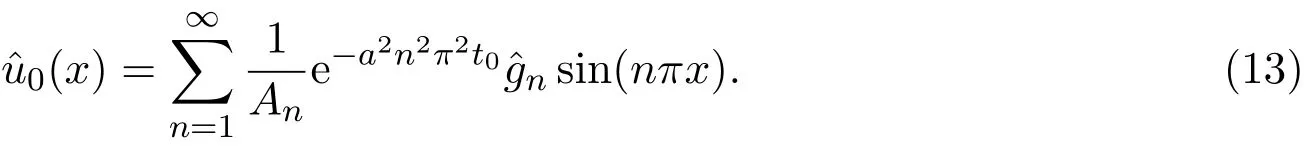
在(13)式基础上可得到最优预报值:
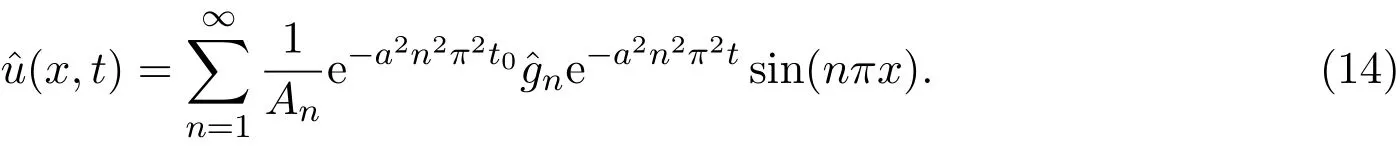
为方便,令
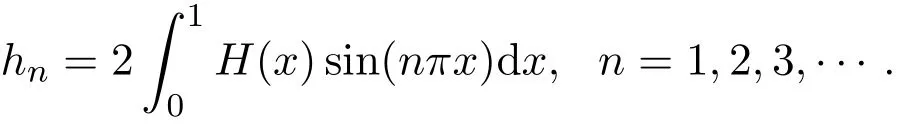
由(12)可得
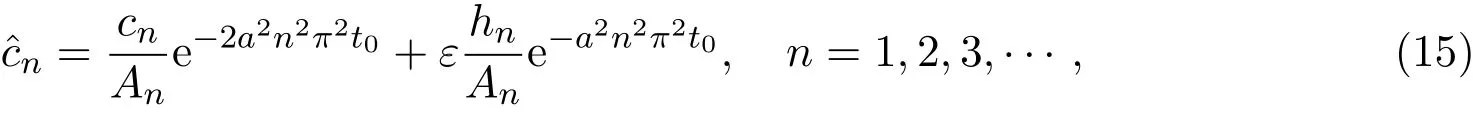
即
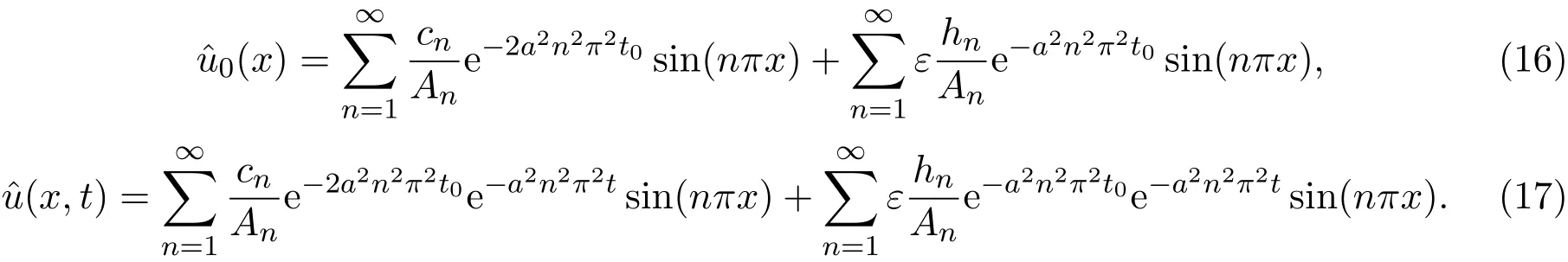
初值误差和预报误差分别为:
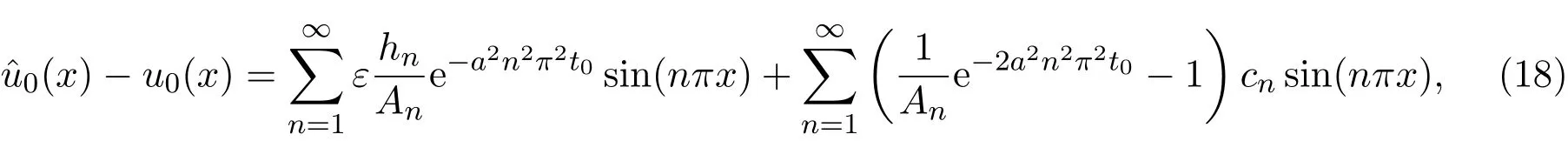
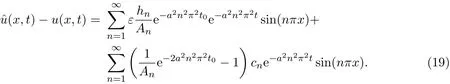
由公式(18)和(19)可以看出:误差由两部分组成,第一部分是由于观测误差ε引起,第二部分是由变分方法引起.
引理4.1
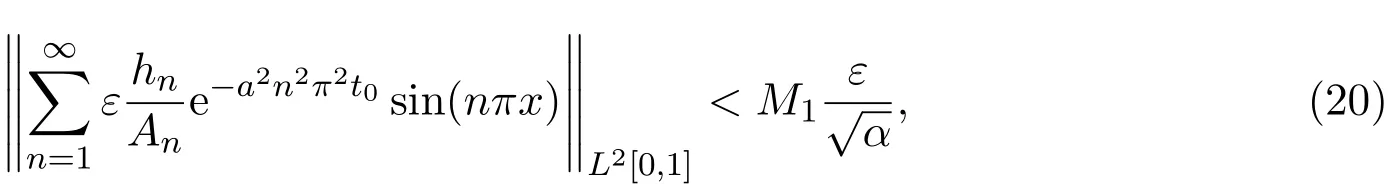
证明考虑到
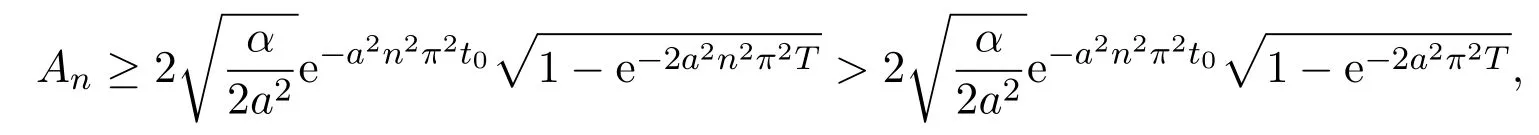
因此
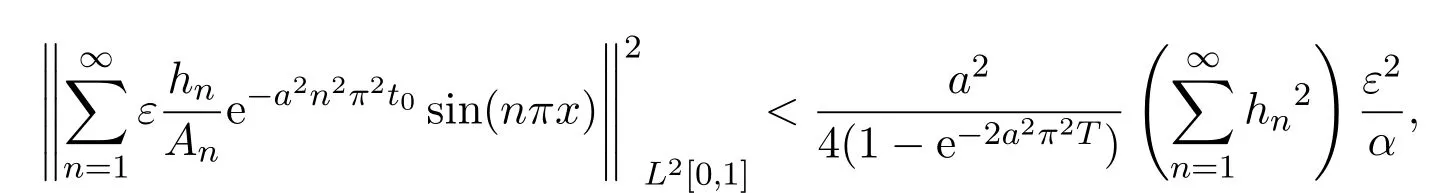
利用贝塞尔不等式得到引理4.1.
引理4.2
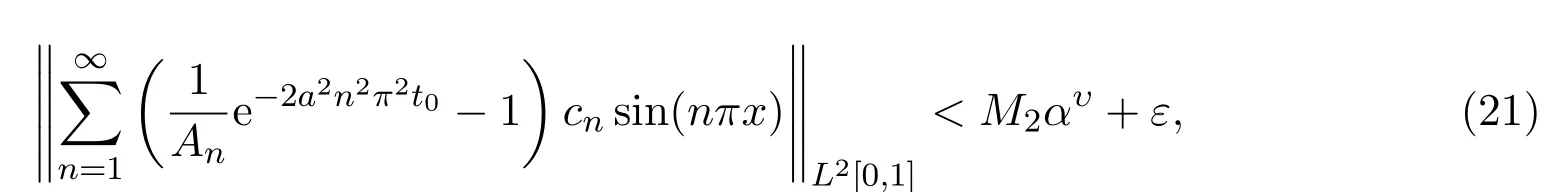
其中
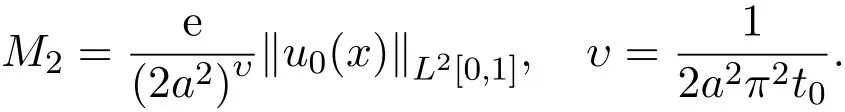
证明由于
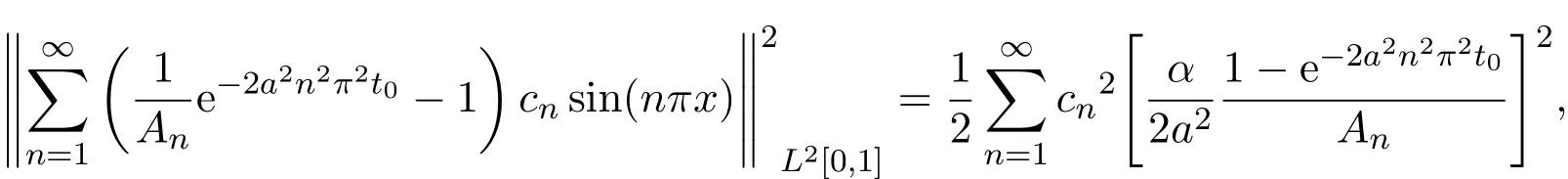
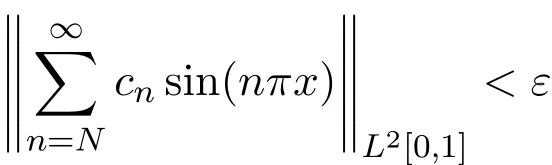
成立.因而
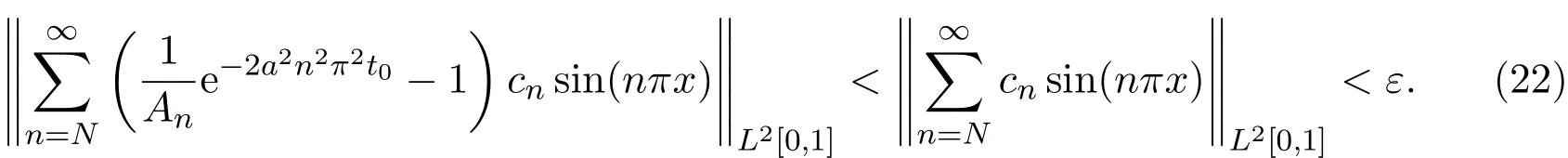
而当n 由Young不等式可证: 由(22)式和(23)式可得引理4.2. 定理4.1 证明由引理4.1、引理4.2易得(24)式.由(19)可知 因此由(24)和(26)得到(25)式. 注4.1定理4.1分别对文献[2]中估计式(2.11)、(2.13)进行修正. 定理4.2当正则化参数α满足必要条件: (2)如果α=O(εη),收敛精度最优达到 证明由定理4.1可得,正则化参数α满足必要条件(27)式时, (2)如果α=O(εη),则 注4.2定理4.2对文献[2]中收敛精度进行修正、补充. 例1选择函数 为稳定泛函,β>0为正则化参数,目标泛函如下: 解求解方法同前面,略去步骤,得到 新的反演初值和预报值为 以初值误差为例, 由于级数 由此例可见,正则化方法中稳定性泛函的选取并非随意的,它必须要保证反问题的适定性.比较公式(9)与公式(28),采用的方法完全相同,即在误差极小模泛函基础上加入稳定性泛函,前者考虑的是系统整体“能量”,后者考虑的是局部“能量”,正是由于稳定性泛函选取不同,导致解的稳定性结果相反.因此,稳定性泛函的选取是提高收敛精度的关键. 论文通过一个简化的模型,在有限的局部观测资料条件下,通过选择适当的稳定性泛函和正则化参数,提出了改进的变分同化方法(即结合正则化的变分同化方法),通过理论分析,证明此方法对于提高预报精度是有效的.因而结合正则化的变分同化方法可应用于许多实际问题,如资料匮乏时的环境、气象、水文模拟与预报等. 论文修正、补充相关计算结果,最后通过一个反例说明稳定性泛函的选取对于改进变分同化方法的重要性.作者认为:在不同的实际问题中,应当结合具体物理背景和具体物理意义,来选取合适的稳定性泛函,以达到最佳稳定性效果. [1]张瑰.变分同化与稳定性中的若干理论问题研究[D].南京:解放军理工大学博士学位论文,2005. [2]Teng Jiajun,Zhang Gui,Huang sixun.Some theoretical problems on variational data assimilation[J]. Applied Mathematics and Mechanics,2007,28(5):651-663. [3]Tikhonov A.N.,Arsenin V.Y.Solutions of Ill-Posed Problems[M].Washington:Winston and Sons,1977. [4]黄思训,伍荣生.大气科学中的数学物理问题[M].北京:气象出版社,2001. [5]张瑰,李振兴.利用局部观测资料对参数进行变分反演的初步研究[J].海洋预报,2008,5(2):59-63. [6]麦宏晏,王连堂.利用远场模式的不完全数据反演声波阻尼系数[J].纯粹数学与应用数学,2009,27(3),566-572. [7]牛俊,方涵先.电离层层析成像及数值模拟[J].应用数学与计算数学学报,2012,26(3):342-347. [8]郭宝琦.抛物型偏微分方程的反问题[M].哈尔滨:黑龙江科学技术出版社,1988. [9]黄思训,韩威,伍荣生.结合反问题技巧对一维海温模式变分资料同化的理论分析及数值试验[J].中国科学:D辑,2003,9:903-911. The stability of variational data assimilation method with local observation data Zhang Gui1,2 The stability of variational data assimilation method with local observation data is researched for the simpli fi ed one-dimensional di ff usion equation.The prediction value of the model is modi fi ed by using the combination of the regularization method with variational data assimilation method,and the prior estimate of the improved variational data assimilation methods are made in theories.By suitable choices of the regularization parameter and stable function,prove that the method is stability for the simpli fi ed one-dimensional di ff usion equation.Some proofs and results are revised and complemented in this paper,and fi nally give an example to illustrate the importance of selecting for the stability functional on the improved variational data assimilation methods. local observation data,variational data assimilation,regularization,stability,convergence rate O29;P413.2 A 1008-5513(2014)03-0221-08 10.3969/j.issn.1008-5513.2014.03.001 2013-12-10. 国家自然科学基金(41206163,41105012);解放军理工大学预研基金;热带海洋环境国家重点实验室(中国科学院南海海洋研究所)开放基金(LTO1205). 张瑰(1973-),博士,副教授,研究方向:反问题与变分同化方法;稳定性问题. 2010 MSC:90A16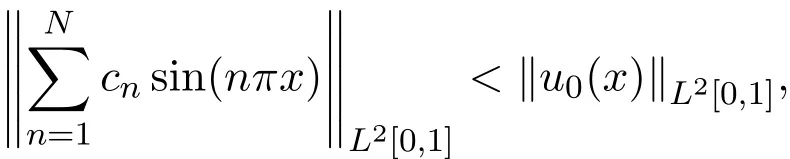
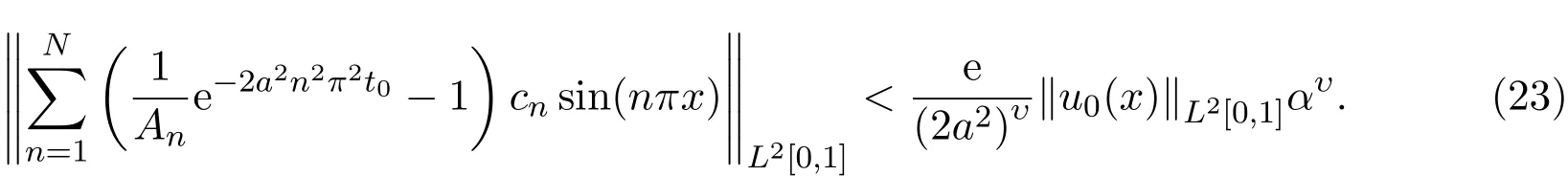
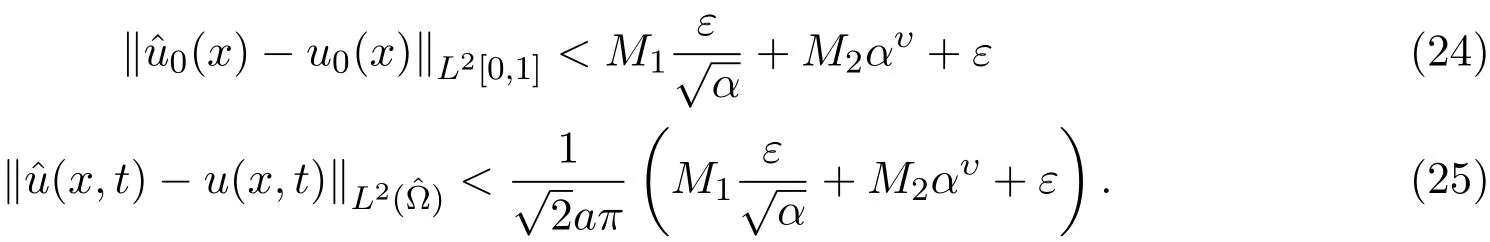
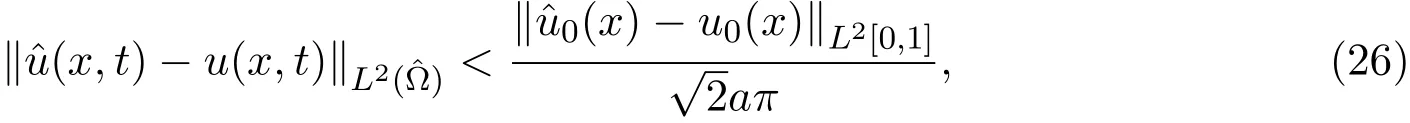

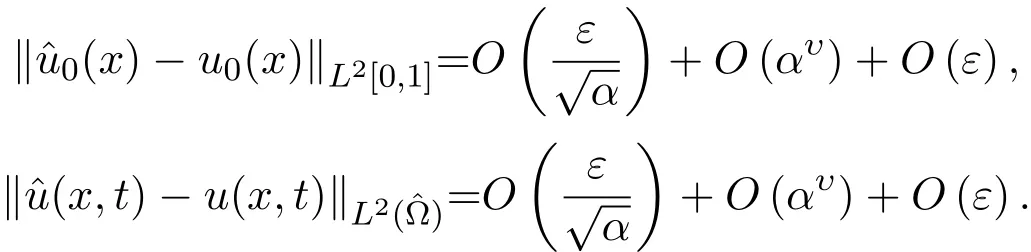
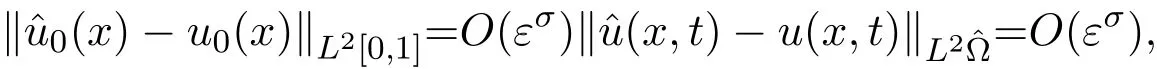
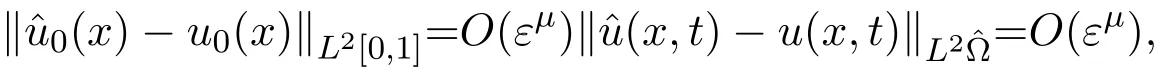
5 稳定性泛函失效的一个反例
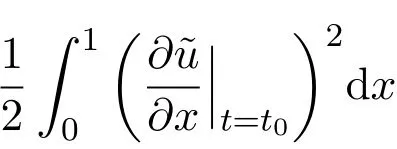
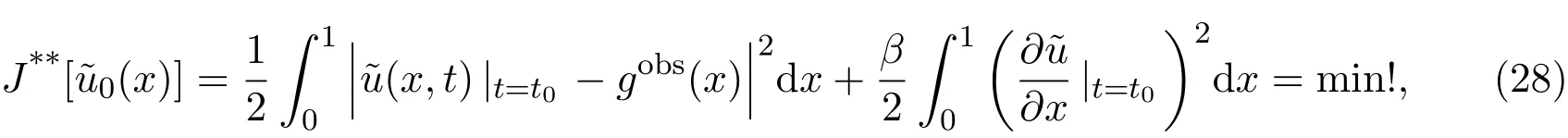
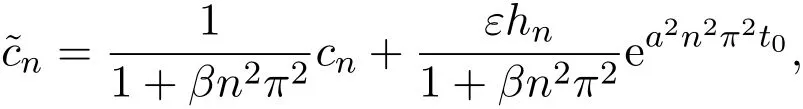
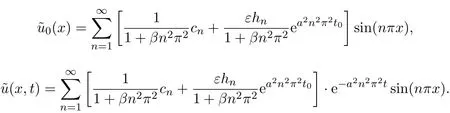
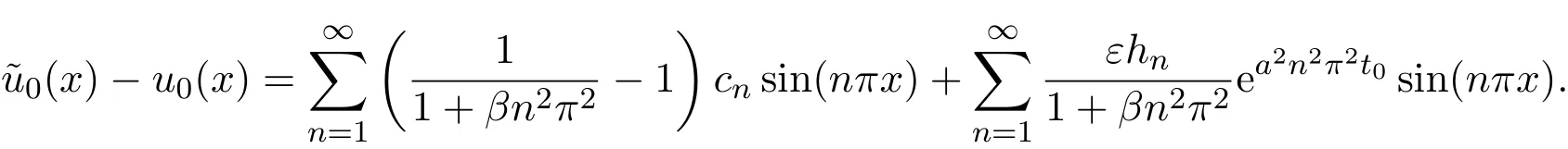
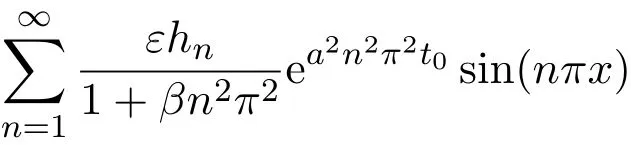
6 结语
(1.Department of Mathematics,Institute of Science,University of Science and Technology,P.L.A., Nanjing211101,China; 2.State Key Laboratory of Tropical Oceanography
(South China Sea Institute of Oceanology Chinese Academy of Sciences),Guangzhou510301,China)
