关于SOL流形具有常平均曲率旋转曲面的注记

马红娟,郑喜英,初元红

(黄河科技学院信息工程学院,河南郑州450063)

关于SOL流形具有常平均曲率旋转曲面的注记

马红娟,郑喜英,初元红

(黄河科技学院信息工程学院,河南郑州450063)

研究非欧流形SOL空间上共形平均曲率方程的可解性,通过研究轮廓曲线对具有平均曲率的旋转曲面进行分类.当这些旋转曲面的平均曲率为给定函数时,计算出相应轮廓曲线的微分方程.通过求解这些微分方程,给出旋转函数是其上共形平均曲率的充分条件.

SOL流形;旋转曲面;平均曲率;共形度量

1 引言及预备知识

随着数学的发展,非欧几何学已成为一门重要的数学分支.在非欧流形中,Thurston几何SOL流形是研究广泛的一类空间.因为它与三维Euclidean流形有很多相似之处,数学工作者们做了大量的研究工作[1-3].Kenmotsu分别讨论了三维Euclidean流形中的常平均曲率的曲面及三维Euclidean空间中的给定平均曲率的旋转曲面[4].但是在非欧流形Thurston几何SOL流形中还没有讨论过给定平均曲率函数的旋转曲面,本文在SOL流形中讨论共形平均曲率的旋转曲面.

定理1.1非欧SOL流形中紧致光滑曲面,存在着与共形度量对应的常平均曲率旋转曲面.

非欧SOL流形是Thurston的八个几何体之一,对R3赋予度量

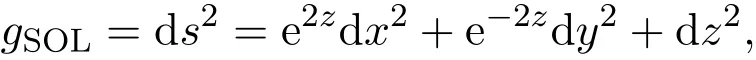
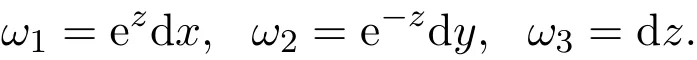
正交基为:

Levi-Civita联络和李括号为:

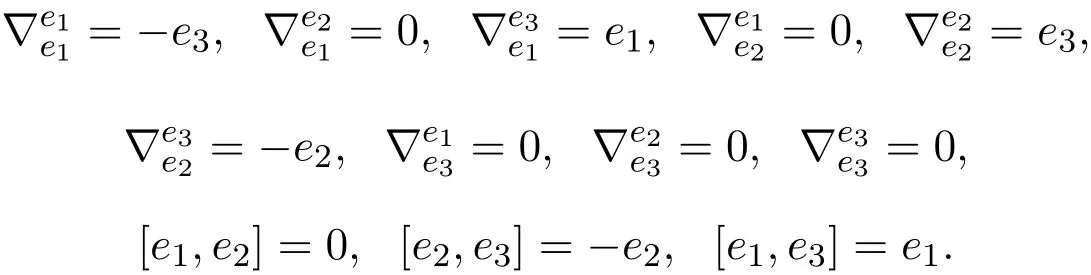
黎曼曲率算子:

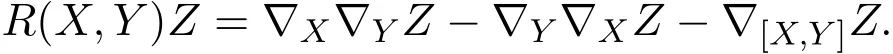
黎曼张量:

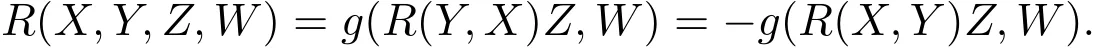
黎曼曲率:

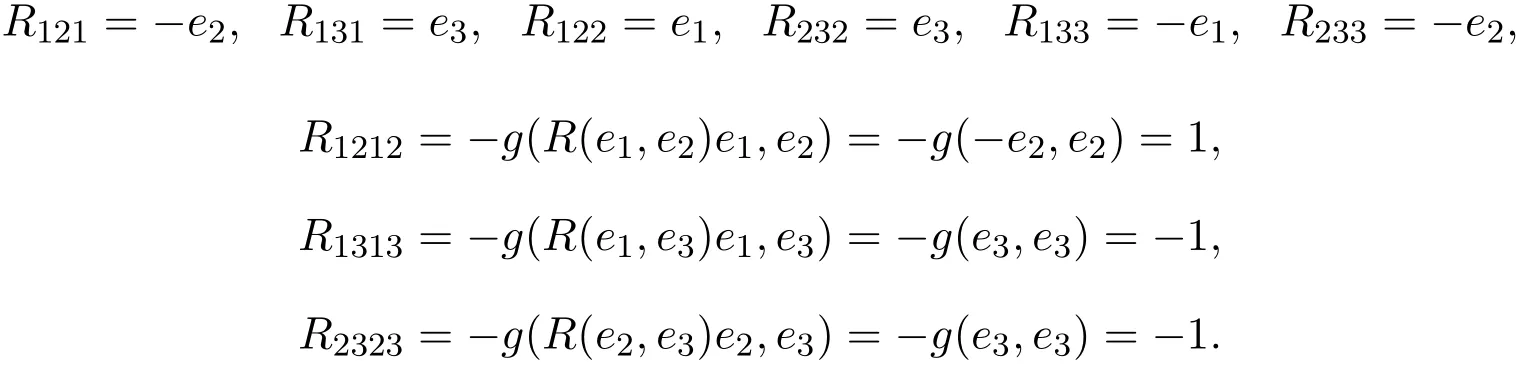
2 结构方程

在R3中考虑柱面坐标(x,ρ,θ),对应笛卡尔坐标(x,y=ρcosθ,z=ρsinθ)(见文献[5]),考虑浸入:

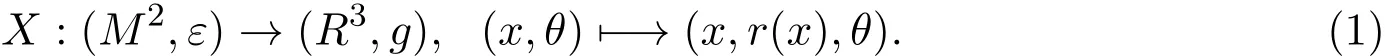
旋转曲面:

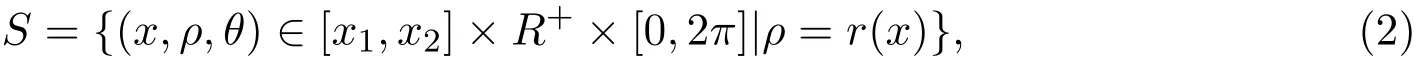
其中r(x)≥0,∀x∈[x1,x2],r(x1)=0=r(x2).欧式度量矩阵为:

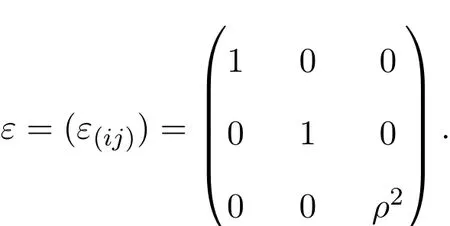
事实上:

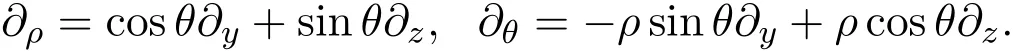
考虑共形度量:

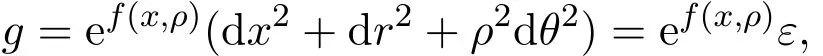
新的矩阵为:

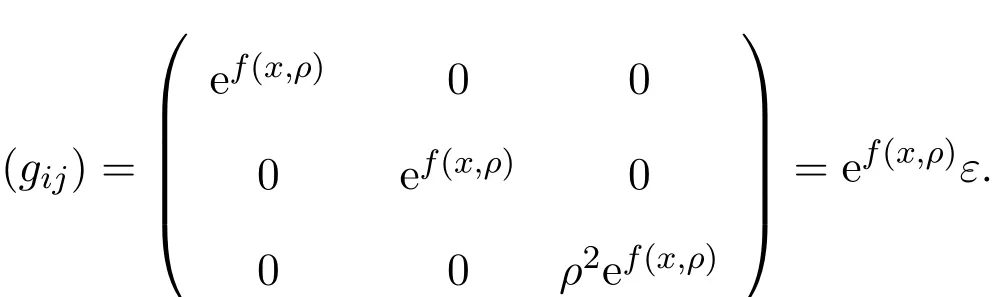
取单位向量:

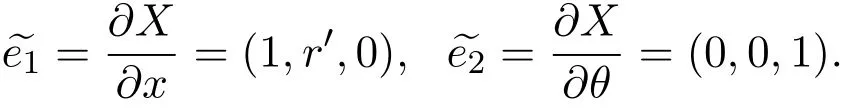
因此,

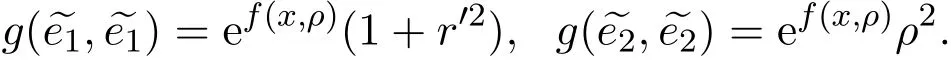
单位正交标架:

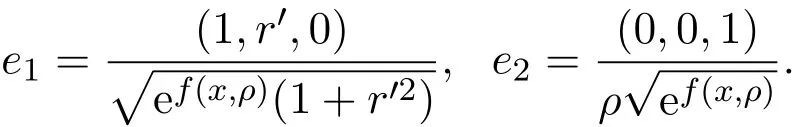
法向量:

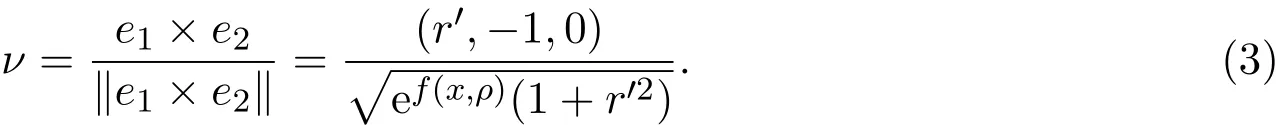
3 Christofffel符号

设x=x1,ρ=x2,θ=x3,利用公式(见文献[6]),其中

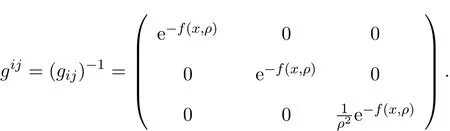
当m=1时,

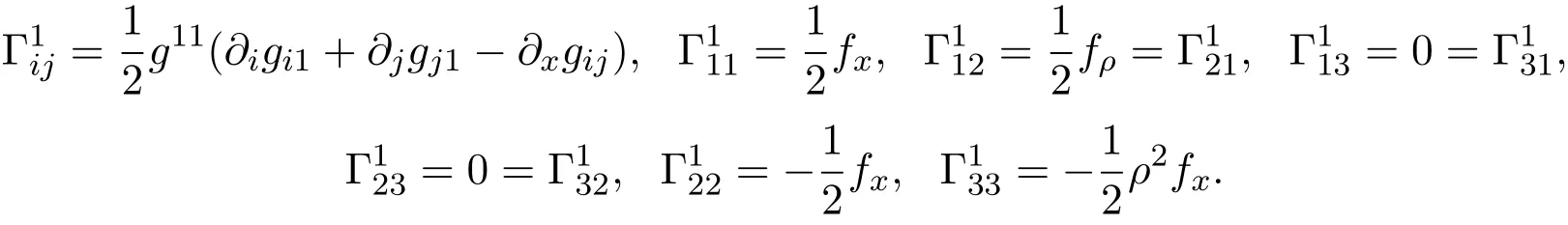
当m=2时,

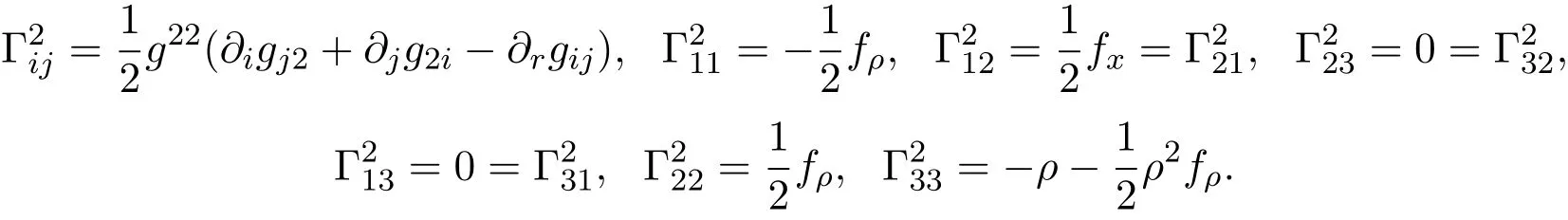
当m=3时,

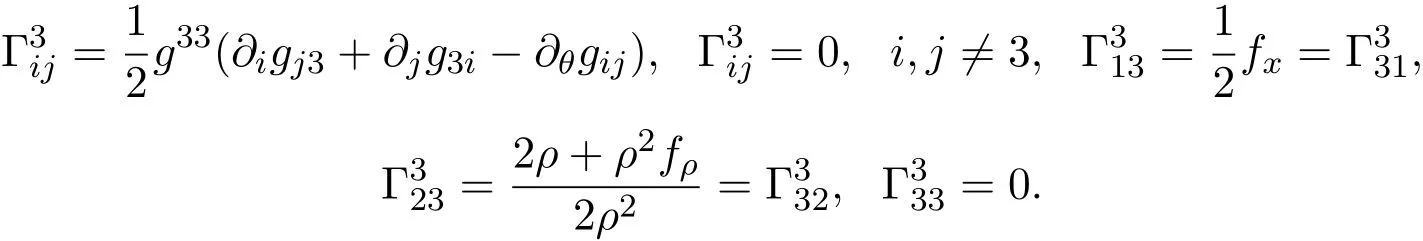
4 平均曲率

在R3中存在紧致不变光滑曲面S有平均曲率对应于ε的共形度量g(见文献[7]),

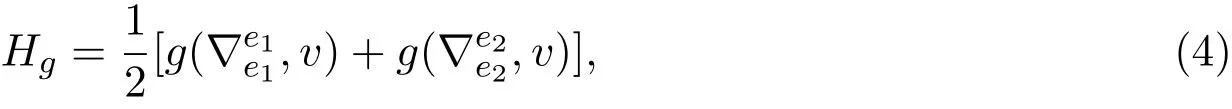
其中∇是Levi-Civita联络,记

其中

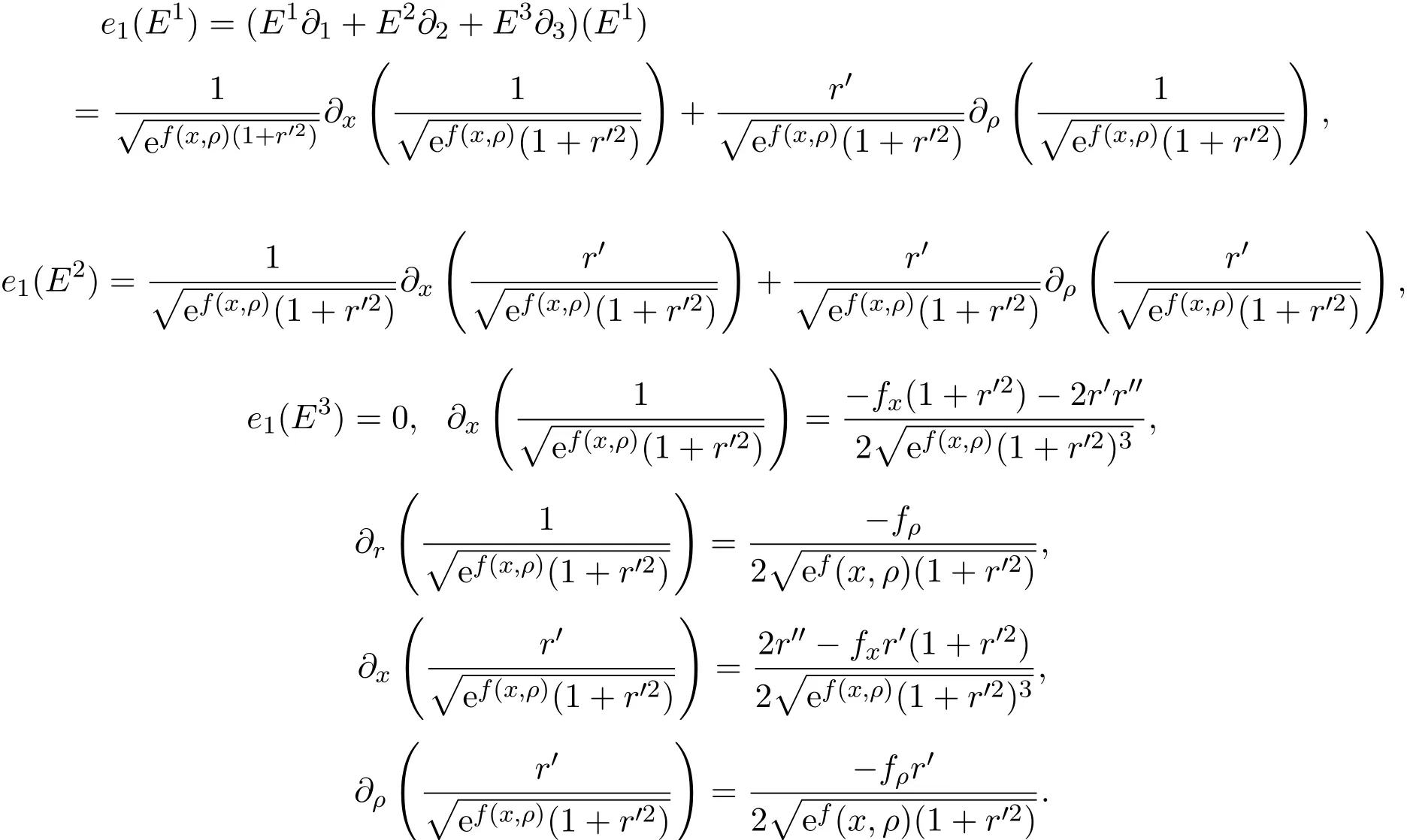
代入(5)式中,有

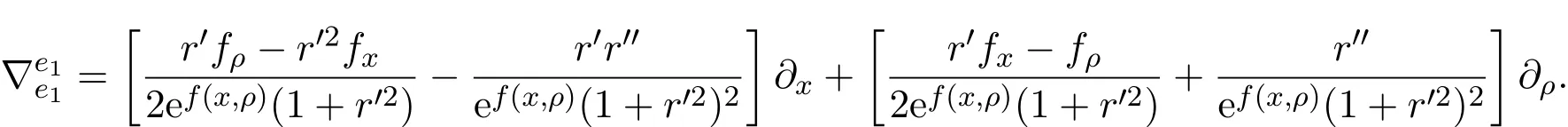
同理

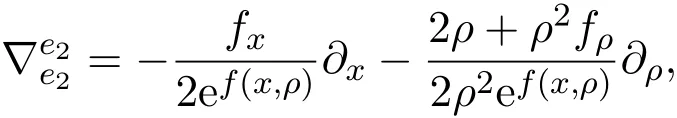
于是得到

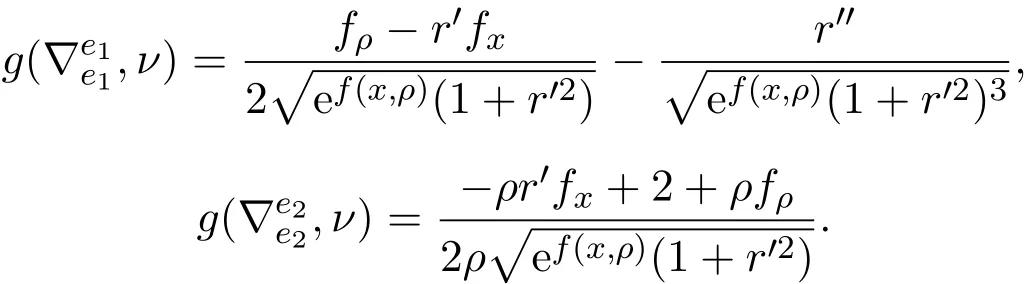
在R3中存在紧致不变光滑曲面S有常平均曲率对应于g的共形度量[8-9],

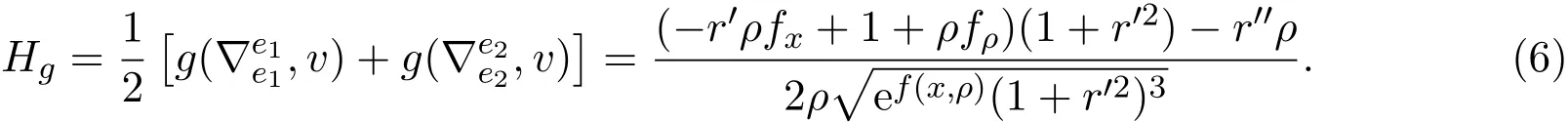
为方便记,引入变量t=ρ−r(x),使得当t=0时曲线ρ=r(x),在新坐标(,t)=(x,ρ−r(x)),有

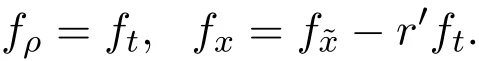
整理得

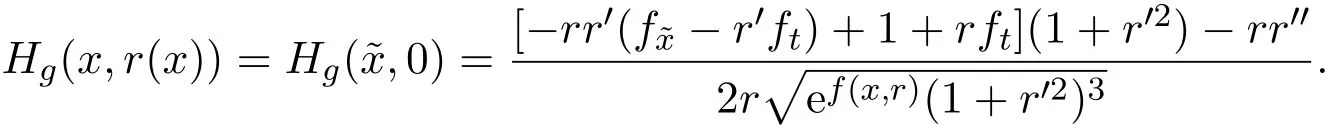
有f(˜x,0)=0,f˜x=0,f=0,代入得

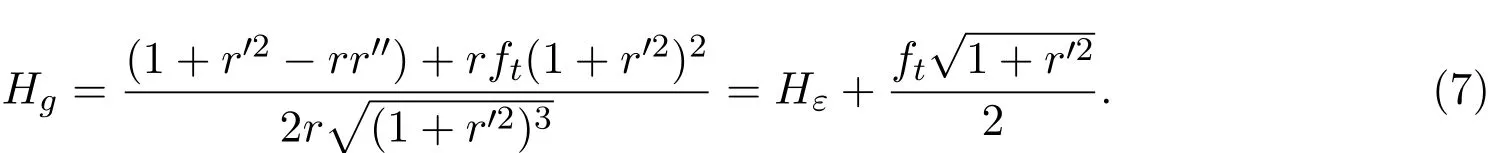
其中Hε是欧式空间光滑曲面S对应于度量ε的平均曲率.

5 讨论

(2)设S=S(R)为半径为R的球,则

因此

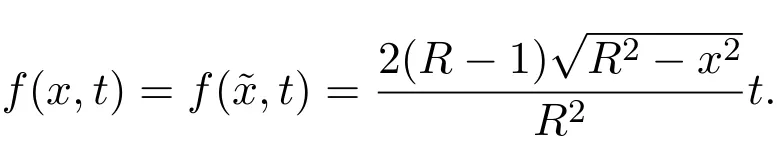
综上可得S(R)在(R3,g)有对应的共形度量g=ef(x,ρ)ε.

6 结论

非欧流形SOL空间中具有常平均曲率的旋转曲面的分类定理:SOL流形中具有常平均曲率的紧致光滑的旋转曲面,存在着共形平坦的黎曼度量.

[1] Wente H C.Counterexample to a conjecture of H.Hopf[J].Paci fi c J.Math.,1986,121:193-243.

[2] Kapouleas N.Constant mean curvature surfaces constructed by fusing Wente tori[J].Invent.Math.,1995, 119:443-518.

[3] Colazingari E.A note on constant mean curvature surfaces in non-Euclidean spaces[J].Bollettino U M I, 1997,7:885-894.

[4] Kapouleas N.Complete constant mean curvature surfaces in euclidean three-space[J].Ann.Math.,1990, 131:239-330.

[5] 龚曲华.三维Lorentz空间形式的共形群[J].纯粹数学与应用数学,2010,26(1):115-122.

[6] 马红娟,赵秀兰,郑喜英.关于Gauss-Kronecker曲率为零的极小超曲面的注记[J].湖南师范大学学报:自然科学版,2012,35(6):1-7.

[7] Thas C.Properties of ruled surfaces in the euclidean space En[J].Academia Sinica,1978,6(1):132-142.

[8] Neagu G.Ruled surfaces in euclidian space[J].Algebras Groups and Geometries,2004,21:341-348.

[9] Nadirashvili N.Hadamard′s and Calabi-Yau′s conjectures on negatively curved and minimal surfaces[J]. Inventiones Mathematicae,1996,126:457-465.

A note on revolution surfaces with constant curvature in SOL manifold

Ma Hongjuan,Zheng Xiying,Chu Yuanhong
(Institute of Information Engineering of Huanghe Science and Technology College,Zhengzhou 450063,China)

The conformal mean curvature equation in SOL manifold is studied.According to the characteristics of the conformal metric,the revolution surfaces in SOL manifold are obtained through a pro fi le curve revolving respectively.Assuming that the mean curvatures of these revolution surfaces are certain functions,the corresponding di ff erential equations about the pro fi le curves can be obtained.By solving these di ff erential equations, the sufficiant condition of the revolution function with conformal mean curvature is achieved.

SOL manifold,revolution surface,mean curvature,conformal metric

O186

A

1008-5513(2014)05-0474-06

10.3969/j.issn.1008-5513.2014.05.006

2014-04-024.

国家自然科学基金(61304175);河南省教育厅科技攻关项目(14B110024);河南省科技局重点项目(20141374).

马红娟(1979-),硕士,讲师,研究方向:微分几何与概率.

2010 MSC:53C42