我国动态利率期限结构的实证分析-广义矩方法

唐恩林

（淮南师范学院经济与管理学院，安徽淮南 232038）

我国动态利率期限结构的实证分析-广义矩方法

唐恩林

（淮南师范学院经济与管理学院，安徽淮南 232038）

本文结合了我国当前利率风险管理的实际情况，采用了较为合适的模型参数估计方法-GMM方法，用最新的一日银行间回购利率，分别对Vacicek，CIR和Ckls三个模型进行了实证。另外，运用时效性原则处理了瞬时利率替代变量问题，最终采用了最新的一日银行间回购利率进行拟合，得出了Vacicek模型能更好的解释我国短期利率的结论。

IBR001；广义矩方法；利率期限结构

作为金融市场上极具有影响力的变量，利率始终成为经济学家研究的热点和难点之一，然而利率也存在着众多的分类，即短期利率和长期利率等，其中短期利率会对金融衍生产品和固定收益债券等金融工具的影响更为直接。在我国，无风险利率经常被用作基准利率来进行资产定价、利率风险管理和收益率曲线的分析。此外，无风险短期利率也直接或间接决定了货币政策的传导机制。然而，我国当前还没有充分实现利率市场化，因为在我国市场经济还未走向成熟的时候，利率的变动并不是随机的，而是由人民银行根据经济的变动形势进行人为的调整。针对我国的利率风险管理现状，从国外引进利率期限结构并运用GMM（广义矩方法）方法进行实证分析具有一定的意义。GMM方法是由汉森于1982年提出，这种参数估计方法适用于模型实际参数满足一些矩条件的基础上。GMM法在继承极大似然估计的优越性，比普通矩法的应用更加广泛，尤其在样本较大时估计结果更加准确。在金融经济学和计量经济学中，GMM方法的应用相当广泛。由于金融经济学和计量经济学通常采用线性结构对经济数据加以处理，然而在实际经济行为中，很多情况并不是线性结构，同时金融变量的增加致使常规的参数估计方法表现出一定的局限性，在这种形式下，GMM估计法产生并逐渐完善，且应用范围越来越广。

1 广义矩估计法

1.1 广义矩估计的基本原理

用β代表α×1参数向量，用wt代表t时期的h×1变量向量，并且h（β，wt）即是r×1的向量值函数h∶（Rα×Rh）→Rr的一个映射。h（β，wt）和wt一样，也是一个随机变量向量。如果E｛h（β，wt）｝=0，那么E｛h（β，wt）｝=0就是r个正交条件。用Yn（w′n，w′n-1，…，w′1）表示n的包含容量的样本中全部观察值的nh×1向量，令r×1向量值函数m（β，Yn）为h（β，wt）的样本均值，因此m（β，的一个映射，选择参数向量β的估计值βn，使得m（β，Yn）无限趋向于0，那么βn就成为广义矩的估计值。令m（β，Yn）=0，用r个方程构成一个方程组解α个未知变量：r=α的结果正是表明方程组只有一个解；r＞α反映的是一般的情形。从这个意义上说，GMM实际上就是将q=m（β′）W-1m（β）求极小化的情况，上式中W为某正定矩阵。GMM估计量就是极小化q而得出的参数估计量βˆ，因此βˆ= argmin（m（β）′W-1m（β））。

1.2 权重矩阵的选择

权重矩阵是GMM估计方法中最重要的问题，在权重矩阵的选择问题上，在常规条件下一般先给予模型相等的权重，然后用这样的参数来计算权重矩阵。1982年Hansen提出了最优权重矩阵：

至于l的确定，即选择的l要使得随机误差项滞后大于l的序列相关性趋于无穷小，其中β～是使W=L得出的估计量。

观测一个普通的具有r个观测值为（y1，y2，…，yr）的线性模型，（y1，y2，…，yr）的平均值为μi，μ2，…，μr，可以简单地表达为μˆi=yi，i=1，2，…，r。在线性限制时，对于μ用广义最小二乘法估计效果最好。因此μ的GLS估计是μˆ=argmin（（Y -U）′Ω-1（Y-U）），式中的Y=（y1，y2，…，yr）′，U=（μ1，μ2，…，μr）′且Ω=E［（Y-U）（Y-U）′］是Y-U的方差-协方差矩阵。因此Ω-1就是本例中最优权重矩阵。

1.3 GMM的估计量分布

1.4 GMM估计法的步骤

GMM的估计步骤为如下三步骤：

当模型不存在序列相关时，L=1；

当模型存在序列相关时，采用广义差分法判断L的取值。

（3）求GMM估计量，在βˆ= argmin（m（β′）W-1m（β））中将权重矩阵的估计量代入即可。

1.5 正交性条件

如果总体的正交条件可以由先验信息或者经济理论得到，那么一般情况下它具有E［h（Y，X，β）］=0的形式，那么选择（Y，X），h（Y，X，β）就为β的R×1向量（R≥K）。与总体的正交条件相对应，本文建构样本矩GMM的原理就是要使m（Y，X，β）′W-1m（Y，X，β）极小化，式中的权重矩阵W最佳的选择结果是var［m（·）］的一致估计。若确定了最佳的W且在条件矩成立的前提下，那么m（Y，X，β）′W-1m（Y，X，β）的极小化值就应当渐近服从于自由度为R-k的χ2分布。

正交性条件具有非常大的意义，以下以Y= Xβ+μ作为例子说明。在计量经济学模型中，基本上都有若干条苛刻的假设前提，而且模型基本上包含了与被解释变量有一定关联的变量，同时，对于随机误差项有一定的要求，即同方差且符合正态分布。不过在实际中很难找到这样的合适条件，往往存在着这样那样的特殊情况，如模型的异方差性，而造成此现象的原因在于模型没有应用到一些对被解释变量具有一定程度影响的变量，因此为了估计出最精确的参数应该应用到的解释变量的个数便显得非常，而GMM方法指出只要符合矩条件E（X′μ）=0即可。

2 动态利率期限结构的实证分析

2.1 样本数据的选择

在考虑动态利率模型的时候通常认为瞬时利率满足一个随机微分方程，然而在现实金融市场上，瞬时利率却是没有的，所以学者通常采用短期利率来代替瞬时利率，而最经常用来代替无风险瞬时利率的利率品种有银行间同业拆借利率和银行间回购利率两种。从金融市场的参与者来观察，同业拆借大多是银行机构参与且不涉及债券市场，市场容量并不大，因此就不可以用来反映债券市场价格符号和市场利率传递。但是相比较银行间同业拆借利率，与债券市场有一定关联的机构基本上都会参与到银行间的回购中去，所以说回购利率数据相比银行间同业拆借利率就更可以传递整个债券市场的资金供需和利率波动信息。另外，从成交额来观察，债券市场的成交总量远远大于同业拆解市场。此外，我国银行间债券市场的回购交易的质押品是国家主权级别的债券，因此是基本上无风险的，可以说回购利率就是无风险利率，能够精确传递短期收益水平和市场资金成本的信息，能够准确地刻画中国金融市场的资金供求动态。所以，本文将使用银行间质押式回购利率代表瞬时利率替代变量。

利率品种的选择将严重影响实证的结果，因此选择标准就显的尤为重要，现阶段我们的银行间质押式回购利率一共有13个品种，这里我们运用相关性和成交性原则来作为替代利率选择的依据，根据国内的研究结果：一日和七日回购利率（分别简称为R001和R007）这两种利率均满足相关性原则，然而有许多研究者最终选择的是R007，其原因在于R007的历史成交额要比R001大。然而，顾及我国的利率市场具有自己的一些特征，在考虑相关性原则和成交量原则的同时更应该考虑时效性。因为利率模型最佳的代表会随着时间段的变化而出现不同的最佳代表变量，所以时效性原则对于中国还不太成熟的利率市场而言就格外重要。最新的数据显示，R001的交易量近些年来明显超过R007，结合我国金融市场的特点，我们最终在瞬时利率的替代变量上使用R001。从wind数据库中，本文使用了2008年3月31到2013年7月20日这段时间的数据。这里要对直接获得的数据R做连续复利计算，即按照公式r =ln（1+R/365）×365处理。

2.2 模型的选择和转换

这里运用了三个最典型的单因素利率模型Vasicek，CIR以及Ckls来拟合我国货币市场数据。由于它们都是采用微分方程的表达形式，所以要事先对它们进行离散化。

下面用GMM方法对Vasicek，CIR以及Ckls这三个模型进行参数估计。三个方程相对应的矩条件分别为

Vasicek模型：

2.3 实证过程和结果分析

本文选取了2008年3月31到2013年7月20日的银行间一天回购利率（yt），除去一些缺失的数据，总共有1 477个样本点。运用SAS编程得出结果如表1所示。

表1 SAS编程结果图

从表1中可以看出：

1）Vasicek模型中α，β和σ在99%的置信水平上是显著的；CIR模型的估计参数中，α和β在95%的置信水平上是显著的，σ在99%的置信水平上显著；CKLS参数估计中，α，β和γ在95%的置信水平上是显著的，而σ只在95%的置信水平上显著。

2）从模型参数是否显著上可以得知模型的拟合效果，因此Vasicek模型的模拟效果是比较好的。Vasicek模型的整体拟合度为0.052 1，这在三个模型中是最大值。因此，综上所述，Vasicek是三个模型最为理想的模型。

接下来再对一天回购的均值进行估计。利率期限结构的离散表达式为

表2 三模型一天回购的回复均值估计

从表2知CIR和Vasicek两模型的均值非常相近，说明这两模型对我国利率期限结构动态拟合的适用性非常高。此外，可以计算出CIR和Vasicek的平均值为1.931 5%，这反应出我国自从2007年之后，银行间1天回购的长期水平为1.931 5%，实际上这个长期水平1.931 5%就是短期利率的均值回复水平。

现在观察Vasicek模型的微分方程形式：

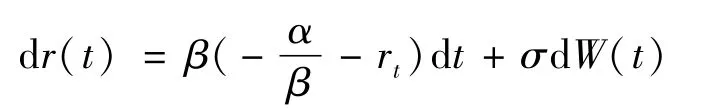
将之前的估计结果带入微分方程中可得：

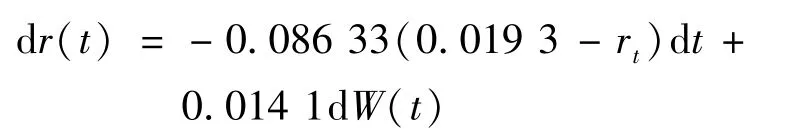
-0.086 33（0.019 3-rt）就是漂移项，0.086 3表示利率稳定的均值回复的速度，这里0.019 3起到了临界值作用，即r＜0.019 3，漂移项＞0，r的运动趋势向上；当r=0.019 3时，漂移项=0，r的趋势保持不变；当大于0.019 3时，漂移项＜0，r的运动趋势为向下。这显著地反映了我国利率的均值回复特征，即利率的长期水平是0.019 3。

3 结 论

本文采用GMM方法，用最典型的三个单因素利率期限结构模型Vasicek，CIR以及Ckls来对瞬时利率的替代利率R001进行了拟合，研究发现Vasicek是三模型中最适合中国利率期限结构的模型。通过对利率期限结构进行离散形式的表达，得出利率均值的表达式为然后根据广义矩参数估计方法计算出一日回购利率R001的均值估计，进而得出中国的短期利率的均值回复水平为0.019 3的结论。

［1］郑振龙，林海.中国市场利率期限结构的静态估计［J］.武汉金融，2003（3）：33-36.

［2］朱世武，陈健恒.交易所国债利率期限结构实证研究［J］.金融研究，2003（10）：63-73.

［3］张金清.中国短期利率跳跃行为的实证研究［J］.统计研究，2008（1）：59-64.

［4］谢赤，吴雄伟.基于Vasicek和CIR模型中的中国货币市场利率行为的实证分析［J］.中国管理科学，2002（6）：22-25.

［5］潘婉彬，陶利斌，缪柏其.利率期限结构模型非线性建模［J］.中国管理科学，2008（5）：17-21.

［6］潘冠中，邵斌.单因子利率模型的极大似然估计一对中国利率的实证分析［J］.财经研究，2004，30（10）：62-69.

［7］穆海权，余雪红，郭伟.从敏感性缺口看利率风险的暴露及后果［J］.财经科学，1998（4）：34-36.

［8］罗大伟，万迪昉.银行股东权益的银行利率弹性银行利率风险的测度［J］.中国管理科学，2002（10）：26-28.

［9］卢庆杰，唐国兴.利率市场化与商业银行利率风险管理［J］.上海经济研究，2003（4）：52-59.

［10］李苇莎.利率市场化趋势下商业银行资产负债管理的应对之策［J］.上海金融，2002（10）：42-44.

［11］S.S.Eduardo，N.T.Walter.Prepayment and the Valuation of Mortgage-Backed Securities［J］.The Journal of Finance，1989（2）：375-392.

［12］Hans van Leeuwen，Michiel Lodewijk.Identification and Pricing of the Embedded Option in a Supplementary Disability Insurance［J］.The Geneva Papers on Risk and Insurance，2001（1）：132-144.

［13］D.Heath，R.A.Jarrow，A.J.Morton.Bond pricing and the term structure of interest rate：A new methodology for contingent claims valuation［J］.Econometrica，1992（60）：77-105.

［14］M.Hopewell，G.Kaufmann.Bond price Volatility and Term to Maturity：A Generalized respecification［J］.American Economic Review，1973（63）：749-753.

［15］J.Hull，A.White.The pricing of option on assetswith stochastic volatilities［J］.Journal of Finance，1987（42）：211-287.

［16］J.H.Lee，D.R.Stock.Embedded Options and Interest Rate Risk for Insurance Companies，Banks and other Financial Institutions［J］.The Quarterly Review of Economics and Finance，2000（40）：169-187.

Empirical Analysis of Dynam ic Interest Rate Term Structure Based on GMM

TANG En-lin
（School of Economics and Management，Huainan Normal University，Huinan 232038，China）

Based on China's current interest rate riskmanagementsituation，and according to the three famousmodels such as Vasicek，CIR and Ckls in dynamic interest term structure，this paper uses GMMto empirically analyze the interest term structure in China.At the same time，this paper chooses substitute variable of spot interest，on the basis of summarizing other research result.The author finally applies the new buyback interest of bank in one day，and concludes that Vacicek model can explain the short interest better in china.

IBR001，GMM，interest term structure

F830

A

1007-4260（2014）03-0036-05

时间：2014-9-15 16：07 网络出版地址：http：//www.cnki.net/kcms/doi/10.13757/j.cnki.cn34-1150/n.2014.03.010.html

2013-10-17

唐恩林，男，安徽合肥人，硕士，淮南师范学院经济与管理学院教师，研究方向为金融工程。