二分系数作用下的线性齐次型

孙广人

（安庆师范学院数学与计算科学学院，安徽安庆 246011）

二分系数作用下的线性齐次型

孙广人

（安庆师范学院数学与计算科学学院，安徽安庆 246011）

本文引入了一族置换对线性齐次型的系数作用，推广了M.Bras-Amorós等人提出线性齐次型的概念。特别地，研究了一族置换对一个型的作用为二分系数作用时线性齐次型的基本结构。

型；数字半群；二分系数作用

一个数字半群S是非负整数集合N的非空子集，包含0，加法封闭，且余集G（S）∶=NS有限。记g=#G（S），称之为S的亏格。

Arf半群是数字半群中较为著名的一种类型，它的定义为：对于任意的s1≥s2≥s3∈S，s1+s2-s3∈S；换句话说，对于线性齐次多项式p（x1，x2，x3）=x1+x2-x3，以及任意的s1≥s2≥s3∈S，有p（s1，s2，s3）∈S。文［1］把这一描述推广为关于数字半群线性齐次型的概念：设p（x1，…，xn）为n元整系数线性齐次多项式，S称为承认型p的数字半群，如果对于任意的s1≥…≥sn∈S，有p（s1，…，sn）∈S。

对于型p，一个重要结论为：

满足上述三个条件的型称为容许型。

在文献［1］基础上，本文将考虑和一个型相关的多个型的情况。为此引入n次对称群Sn的一个子集对型p的系数作用：

为H对p的系数作用。一个数字半群S称为承认系数作用PH的，如果对于任意的σ∈H，以及s1≥…≥sn∈S都有p（s1，…，sn）σ∈S。

注1设承认型p的一切数字半群为S（p）。根据定理1（2）可知承认PH的一切数字半群的集合为

本文感兴趣的子集H在于其中所有置换对p的系数作用都是二分的情况。在该作用下描述稳固型与脆弱型的基本结构。

1 二分作用下的稳固型与脆弱型

定义2一个置换σ对于型p的作用如果满足σ（A）⊆A，则称σ对p的作用为二分的。

例1令p=x1+x2-x3，显然σ1=（12）的作用是二分的，而σ2=（13）的作用是非二分的。

定义3设p是容许型，H为对p二分的全部置换。H1为H中一切保持B中数字不动置换，H2为H中一切保持A中数字不动置换，则

（1）如果N承认系数作用PH，则称p为稳固型。反之，若对于任意非恒等置换σ∈H，S（pσ）=Ø，则称p为脆弱型；

（2）如果N承认系数作用PH1，则称p为非负稳固型。反之，若对于任意非恒等置换σ∈H1，S（pσ）=Ø，则称p为非负脆弱型；

（3）如果N承认系数作用PH2，则称p为负稳固型。反之，若对于任意非恒等置换σ∈H2，S（pσ）=Ø，则称p为负脆弱型。

注2显然H，H1和H2都是Sn的子群。

例2由定理1的条件（3），容易判断p=x1+x2-x3，p2=2x1-x2+x3都是稳固的型，p3= 3x1-2x2+x3是脆弱型。

例3p3=2x1-x2+4x3-5x4是非负稳固的，也是负脆弱的。

例4p3=2x1-x2+x3-2x4既是非负稳固型，也是负稳固型，但不是稳固型。

2 等价描述

本节给出稳固型与脆弱型的等价描述。

定理2设p是容许型，集合A与B非空且#A =l，#B=m。令A，B中数按升序排列为：

再令A=｛αi∶i∈A｝，B=｛αj∶j∈B｝，A，B中数分别按升序排列为：

（1）p为稳固型当且仅当pα是容许型；

（2）p为非负稳固型当且仅当pβ是容许型；

（3）p为负稳固型当且仅当pγ是容许型。

证明只证（1），其余两个证明类似。显然α∈H，所以p为稳固型时自然pα是容许型。反之，如果pα是容许型，根据定理1（3）只需证明对于任意的即可。下面证明根据pα是容许型，即证结论。

把集合C=｛ασ（u）∶ασ（u）≥0，1≤u≤n′｝，D=｛ασ（v）∶ασ（v）＜0，1≤v≤n′｝分别按照升序排列

左右两边分别求和后即得。

定理3设p是容许型，集合A与B，A，B如定理2所设。令A，B中数按升序排列为

（1）p为脆弱型当且仅当p=α1x1+α2x2+ α3x3，其中α1，α3，α1+α2＞0，α2+α3＜0；

（2）p为非负脆弱型当且仅当A是1到n之间一些互不相邻的数，αi1＞…＞αil，且对于任意1≤k≤l-1，存在ik≤uk≤ik+1-1，使得Auk＜αik-αik+1；

（3）p为负脆弱型当且仅当B是1到n之间一些互不相邻的数，αj1＞…＞αjm，且对于任意1≤k≤m-1，存在jk≤vk≤jk+1-1，使得Avk＜αjkαjk+1。

证明先证明（2），（3）的证明与之类似。

必要性如果αi1＞…＞αil不成立，则存在1≤x＜y≤l，使得αix≤αiy，这时置换αix，αiy，显然定理1的条件（3）仍然成立，矛盾。其次，如果存在两个下标相邻，形如ix+1=ix+1，由定理1的条件（3）已知Aix-1≥0，所以交换αix，αix+1，条件（3）仍然满足，矛盾。同样原理，如果存在1≤k≤l，使得Ajk+1-1≥αik-αik+1，只要置换αik，αik+1即可。

充分性对于一个非恒等置换（1）≠σ∈H1，必然存在1≤x＜y≤l，σ（ix）＞σ（iy），即ασ（ix）≤ασ（iy），设y0是出现该情况的最小数，x0是对于y0最小满足该关系的数，则有

由于ασ（ix0）＜ασ（iy0）及αi1＞…＞αil，可知存在整数k，满足1≤k≤y0-1，使得

否则任意1≤k≤y0-1，都有σ（ik）=i，特别的σ（ix0）=ix0≤iy0-1＜σ（iy0），与假设矛盾。因此存在整数q，满足1≤q≤y0-1，使得σ（iq）∉｛i1，…，iy0-1｝，或者说由已知条件即得

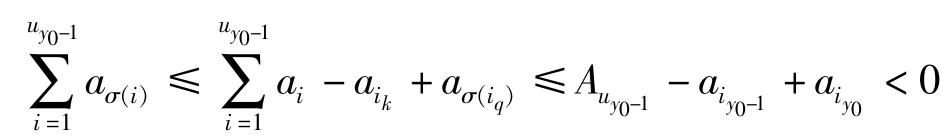
再由定理1的（3）即得。

对于（1），由（2）和（3）可知A即为1到n之间的所有奇数，并且αi1＞…＞αil，αj1＞…＞αjm，A2k＜α2k-1-α2k+1，A2k+1＜α2k-α2k+2，但是如果n≥4，即有α1+α3+α4＜0，而α2＜0，因此α1+α2+α3+α4＜0，矛盾。即证结论。

［1］M.Bras-Amorós，P.A.García-Sánchez.Patterns on numerical semigroups［J］.Linear Algebra Appl.，2006，414（2-3）：652–669.

［2］M.Bras-Amorós，P.A.García-Sánchez and A.Vico-Oton，Nonhomogeneous patterns on numerical semigroups［J］，Internat.J.Algebra Comput.，2013，23（6）：1469-1483.

［3］J.C.Rosales，P.A.García-Sánchez.Numerical semigroups［M］.Volume20 of Developments in Mathematics，Springer，New York，2009：96-98.

Bipartite Act on Coefficients of a Linear Homogeneous Pattern

SUN Guang-ren
（School of Mathematics and Computational Science，Anqing Teachers College，Anqing 246133，China）

This paper introduces acts of a setof permutations on coefficients of a linear homogeneous pattern.This notion generalizes linear homogeneous pattern，which was put forward by M.Bras-Amorós et al..Especially，we investigate basic constructions of patterns when acts of a set of permutations are bipartite.

pattern，numerical semigroups，bipartite acts on coefficients

O151.2

A

1007-4260（2014）03-0007-03

时间：2014-9-15 16：07 网络出版地址：http：//www.cnki.net/kcms/doi/10.13757/j.cnki.cn34-1150/n.2014.03.003.html

2014-02-23

孙广人，男，河北唐山人，博士，安庆师范学院数学与计算科学学院副教授，研究方向为代数与编码。