关于单形稳定性几个不等式的推广

陈士龙

（安徽大学艺术与传媒学院，安徽合肥 230011）

关于单形稳定性几个不等式的推广

陈士龙

（安徽大学艺术与传媒学院，安徽合肥 230011）

本文研究了En中n维单形的稳定性，在总结已有结论的基础上，对单形的稳定性进行了推广，同时也给出了单形几何不等式的新的稳定性版本，改进了已有的结论。

n维欧氏空间En；稳定性；单形；内切球半径；外接球半径

设n维欧氏空间En中的n维单形Ωn的顶点集为｛A1，A2，…，An+1｝，它的棱长为αij=｜AiAj｜（1≤i＜j≤n+1），有时也用表示单形的各个棱长，V表示单形的体积，R和r分别表示n维单形Ωn的外接球半径和内切球半径，Fi（i=1，2，…，n+1）表示单形顶点Ai所对的侧面（n-1维单形）的n-1维体积（面积）。点O是单形的外心，点I是单形的内心，点G是单形的重心。以点I为球心，以r为半径的内切球与单形各侧面的切点为顶点的单形Ω′n称为单形的切点单形。

几何不等式的稳定性最早由Minkowski提出，也称为稳定性版本。文献［1-5］对几何不等式的稳定性概念给出了准确的描述，其具体定义是指在一些含有等号的几何不等式中，当其中的几何体为某种特殊的几何体或几何体相似时取等号。假设某几何体使得不等式与相等时相差很小，那么此几何体与去等号的特殊几何体的“偏差”也很小。比如在平面上凸体K的等周不等式

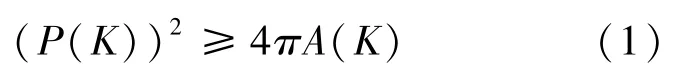
当且仅当凸体K为圆时取等号，其中P（K）与A（K）分别为凸体K的周长与面积。

假设对ε＞0，如果

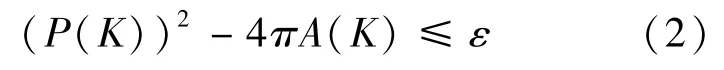
能否断定存在圆B，使得在某种“偏差”度量g（K，B）下，有

这里f（ε）是满足当ε→0时，f（ε）→0的非负实函数。若存在某种“偏差”度量，使得当（2）成立时必有式（3）成立，则称式（1）是稳定的，否则是不稳定的。

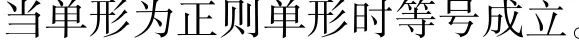
［1］H.Minkowski.Volume und oberflache［J］.Math.Ann.，1903，57：447-495.

［2］Bonnesen.Probl emes des Isop im de Piphanes［M］.Paris：Gauthier-Villars，1929.

［3］P.R.Goodey，H.Groemer.Stability results for first order projection bodies［J］.Poc.Amer.Math.Soc.，1990，109：1103-1114.

［4］R.Gardner，J.，S.Vaddallo.Stability inequalities in the dual Brun-Minkowski theory［J］.J.Math.Anal.Appl.，1999，231：568-587.

［5］H.Grmer.Stability properties of geometric inequalities［J］.A-mer.Math，Monthly，1990，97：382-394.

［6］马统一.Veljan-Korchmaros不等式的稳定性［J］.数学年刊，2008，29A（3）：399-412.

［7］沈文选.单形论导引［M］.长沙：湖南师范大学出版社，2000.

［8］S.G.Yang.An inequality for a simplex and its applications［J］. Geometriae Dedicata，1995，55：195-198.

［9］L.Gerber.The orthocentric simplex as an extreme simplex［J］. Pacific，J.Math.，1975，56（1）：97-111.

［10］陈士龙.En中两个几何不等式的改进［J］.安庆师范学院学报（自然科学版），2011，17（3）：4-7.

［11］杨世国.关于内接单形的一个几何不等式［J］.数学杂志，2003，23（2）：218-220.

［12］匡继昌.常用不等式［M］.济南：山东科学技术出版社，2004：256-257.

［13］沈文选.单形论导引［M］.长沙：湖南师范大学出版社，2000.

［14］M.S.Klamkin.The circumradius-inradius inequality for a simplex［J］.Math Magazine，1979，52（1）：20-22.

［15］沈文选.单形论导引［M］.长沙：湖南师范大学出版社，2000.

［16］毛其吉，左铨如.切点单形的一个几何不等式［J］.数学的实践与认识，1987（4）：71-75.

［17］Klamkin MS.Inequality for s simplex［J］.SIAM.Rev.，1985，27（4）：210-215.

［18］S.G.Yang.Extersions of Klamkin's theorem［J］.Northeastern Math.J.，1991，7（4）：424-427.

Stability of Some Geometric Inequalities for a Simplex

CHEN Shi-long
（School of Arts and Communication，Anhui University，Hefei230011，China）

Using the distance theory andmethod of geometry inequality to study the problem of stability，which is some geometric inequalities for an n-dimensional simplex in the Euclidean space.From the deviation regularmetric of two simplexes，we proved three importantgeometric inequalities for an n-dimensional simplex are all stable，gave the stability versions of these geometric inequalities for a simplex and improved three well-known results.

Euclidean space，stability，simplex，inradius，circum radius

O178

A

1007-4260（2014）03-0004-03

时间：2014-9-15 16：07 网络出版地址：http：//www.cnki.net/kcms/doi/10.13757/j.cnki.cn34-1150/n.2014.03.002.html

2013-06-14

安徽省高校省级自然科学研究课题（KJ2013B043）资助。

陈士龙，男，安徽寿县人，硕士，安徽大学艺术与传媒学院讲师，主要从事距离几何与解析几何的研究。