关于Furuichi猜想的注记

周其生

（安庆师范学院数学与计算科学学院，安徽安庆 246133）

关于Furuichi猜想的注记

周其生

（安庆师范学院数学与计算科学学院，安徽安庆 246133）

本文将Ando和Furuichi关于两个半正定矩阵多重积的迹的一些不等式推广到无穷维Hilbert空间，得到关于算子迹的若干不等式，作为其结果，得出Furuichi猜想在一定条件下对算子迹的肯定的回答。

矩阵；算子；迹；不等式；Hilbert空间；Furuichi猜想

文献［1］介绍了BMV猜想的相关研究成果，并提出一个问题。若A，B是两个同阶半正定Hermite矩阵，记Wm，k（A，B）为长度是m，其中B出现k次的字（即由A，B按通常矩阵乘法组成的单项式（或称多重积）），这样的Wm，k（A，B）共有个。考虑这些字的迹Tr W（A，B）（不一定是m，k实数），我们的问题：是否有

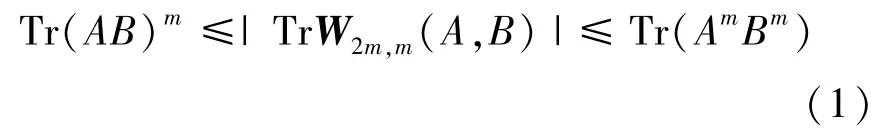
成立？例如Tr（AB）6≤｜Tr（ABA2BA3B4）｜≤Tr（A6B6）成立吗？

我们注意到，即使Tr Wm，k（A，B）是实数，一般不一定有Tr W2m，m（A，B）＞Tr（AB）m，并且可举出一个3×3矩阵的反例。但（1）式是否成立，仍然是未知的。事实上，关于不等式

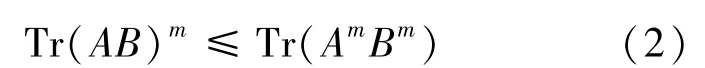
也曾受到广泛关注。在1980年，著名控制论专家R.Bellman教授［2］曾提出（2）式的猜想，后有不少作者围绕该猜想得到很多矩阵迹的不等式。但事实上比不等式（2）更一般的不等式早在1976年就已经出现，后来被称之为Lieb-Thirring不等式［3］，即设A，B≥0，q＞1，k＞0，则有

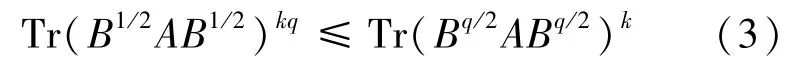
当k=1，q=m时，由（3）式即可得到（2）式。

H.Araki［4］将Lieb-Thirring不等式推广为

定理A（Araki-Lieb-Thirring）对A，B≥0，q≥0，0≤r≤1，下面不等式成立：

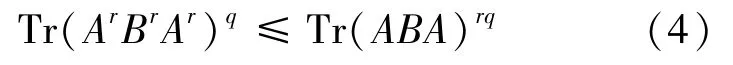
对r≥1，不等式反向。

关于不等式（1）的相关研究尚不多见，T.Ando在1994年［5］和2000年［6］讨论了两个半正定矩阵A，B的多重积，分别得到如下两个结果：

定理B（文献［5］定理4.1）对任意两个同阶半正定矩阵A，B，有

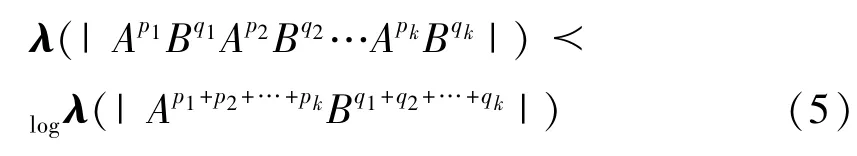
满足0≤p1≤q1≤p1=q2≤q1+q2≤…≤q1+q2+…+qk-1≤p1+p2+…+pk≤q1+q2+…+qk，这里λ（T）表示T的特征值向量。

因为X log-受控于Y，即X≺logY，蕴含X≺ωY［7-8］，因此有

推论1在定理的条件下，有

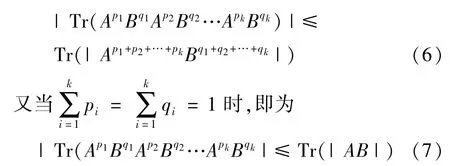
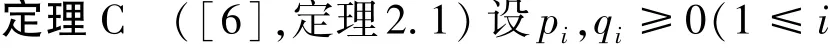
S.Furuichi等人也研究了两个矩阵的多重积，并证明二阶半正定矩阵的情形［9］：

定理D设正数p1，p2，…，pm满足p1+p2+…+pm=1，T，A∈M+（2，C），则有

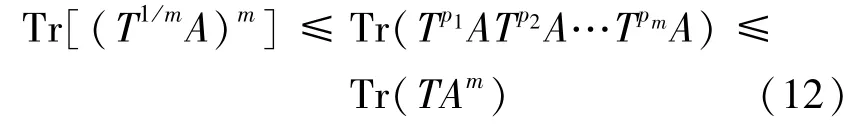
成立。他们提出如下猜想：

Furuichi猜想：若p1+p2+…+pm=1，T，A∈M+（n，C），下面不等式

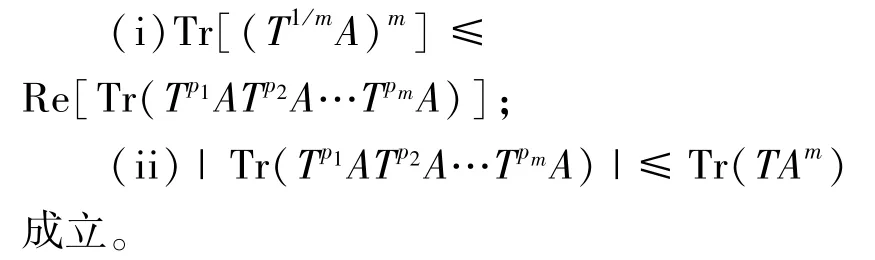
后来，文［10］给出一个反例说明（i）是不对的，但如下不等式

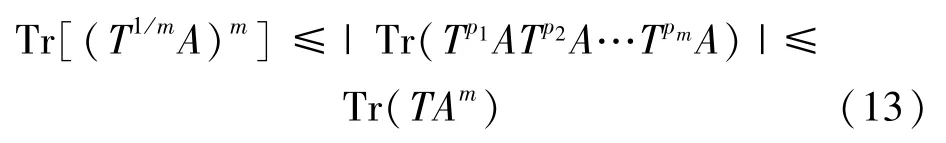
是否成立仍然是未知的。

事实上，定理D中的正数pi（i=1，2，…，m）可以为非负实数。当（6）式中qi为非负整数时，可简化为（12）式的形式。因此，（12）式可看作（6）式的特殊形式，但对于2阶矩阵，不需要pi，qi的限制条件。

本文的目的是将定理B和定理C中的（6），（9）两式分别推广到算子的情形。

本文用B（H）表示可分无穷维Hilbert空间H上的有界线性算子全体，Cp表示B（H）中Schatten p-类算子全体，特别地，C1为迹类算子全体所作成的理想，C+1表示全体正的迹类算子，对算子T∈C1，tr T表示它的迹。关于迹类算子的相关概念和基本性质参见［11］。为简便起见，这里讨论的对象主要是迹类算子，不精细地讨论Cp类。

当A∈B（H）为紧算子时，记｛Sj（A）｝为A的奇异值不增序列。由文献［11］知A∈C+1时，它总可以表示为这里λj（A）为A（包括重数）的特征值，且λ1（A）≥λ2（A）≥…≥λn（A）≥…，ej为其相应的标准正交特征向量。显然当A只有有限个非零特征值时，则∃k使得λj（A）=0（i＞k）。

设A，B为正迹类算子，记

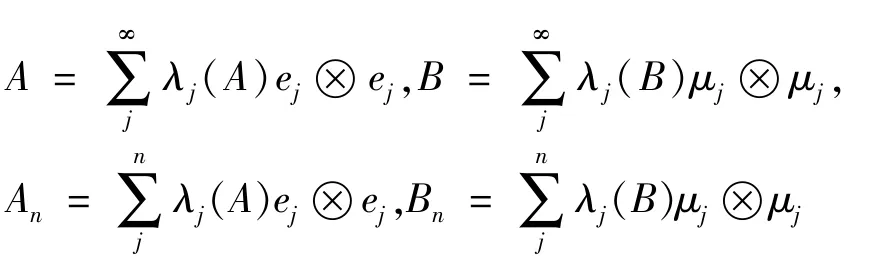
并记Mn=span｛ej；μj∶1≤j≤n｝，mn=dim Mn

利用定理2，在一定条件下猜想1的（ii）是成立的：

定理3设T，A∈C+1，非负实数r1，r2，…，rm满足r1+r2+…+rm=m，0≤r1≤1≤r1+r2≤2≤r1+r2+r3≤3≤…≤r1+r2+…+rm≤m。则

利用以上定理，容易把上述推论2和推论3推广到算子迹的情形。

［1］周其生.关于Bessis-Moussa-Villani猜想［J］.安庆师范学院学报（自然科学版），2013，19（3）：1-5.

［2］R.Bellman.Some inequalities for positive definitematrices［A］. In：E.F.Beckenbach（Ed.），General inequalities［C］//Proceedings of the2nd International Conference on General Inequalities，vol.2，Birkhauser，Basel，1980：89-90.

［3］E.Lieb，W.Thirring.In studies inmathematicalphysics（Eds.E. Lieb，B.Simon and A.ightman）［M］.Princeton Press，1976：301-302.

［4］H.Araki.On an inequality of Lieb and Thirring［J］.Lett.Math. Phys.，1990，19：167-170.

［5］T.Ando and F.Hiai.Log majorization and complementary Golden-Thompson type inequalities［J］.Linear Algebra Appl.，1994，198：113-131.

［6］T.Ando，F.Hiai，K.Okubo.Trace inequalities formultiple products of two matries［J］.Math.Inequal.Appl.，2000，3：307-318.

［7］R.Bhatia.Matria analysis［M］.Springer，New York，1997.

［8］王松桂，吴密霞，贾忠贞.矩阵不等式［M］.第二版.北京：科学出版社，2006：185-224.

［9］S.Furuichi，K.Kuriyama，K.Yanagi.Trace inequalities for products of matrices［J］.Linear Algebra Appl.，2009，430：2271-2276.

［10］S.Furuichi，Minghua Lin.Remark on two conjectures onmatrix trace inequalities［J］.arXiv：1001.3803v4［math.FA］25apr 2010.

［11］R.Schatten.Norm ideals of completely continuous operators［M］.Springer-verlag，New York，1970.

［12］J.Weidmann.Linear operators in Hilbert space［M］.Springer-Verlag，New York，1980：170-172.

A Note about Furuichi Conjecture

ZHOU Qi-sheng
（School of Mathematics and Computation Science，Anqing Teachers College，Anqing 246133，China）

In this paper，we generalize some inequalities of the trace ofmultiple products about two positive semi-definitematrix by Ando and Furuichi to the infinite dimensional Hilbert space，and get some inequalities aboutoperator trace.Consequently，we partly give positive answer to Furuichi's conjecture in infinite dimensional Hilbert space.

matrix，operator，trace，inequality，Hilbert space，Furuichi conjecture

O177.1

A

1007-4260（2014）03-0001-03

时间：2014-9-15 16：07 网络出版地址：http：//www.cnki.net/kcms/doi/10.13757/j.cnki.cn34-1150/n.2014.03.001.html

2014-03-12

周其生，男，安徽金寨人，安庆师范学院数学与计算科学学院教授，主要从事算子理论研究。