关于双曲周期点与双曲周期轨的一种等价性及其证明

王 磊，袁 泉

（1.合肥学院数学与物理系，安徽合肥 230601；2.华中科技大学数学与统计学院，湖北武汉 430074）

关于双曲周期点与双曲周期轨的一种等价性及其证明

王 磊1，2，袁 泉2

（1.合肥学院数学与物理系，安徽合肥 230601；2.华中科技大学数学与统计学院，湖北武汉 430074）

阐述双曲周期点与双曲周期轨的异同，指出双曲周期点与双曲周期轨之间的一种相互蕴含关系，并利用微分流形上微分同胚的保维数性质、复合微分同胚求导法则给予严格证明。

双曲周期点；双曲周期轨；双曲直和分解

紧致度量空间中微分自映射的双曲集是微分动力系统研究的主要对象之一，不变集的双曲性具有很多好的性质，也是我们进一步定义并研究双曲不变流形、公理A系统以及阐述Smale谱分解定理的基础［1，2］。双曲集不但在微分动力系统中占有很重要的地位，而且在研究混沌动力学中也具有重要作用，比如著名的Smale马蹄集就是一个一致双曲集［3］，利用双曲集的性质往往可以给出混沌动力系统一些复杂结果的拓扑几何说明，因此双曲集至今依然是现代动力系统研究的重要方向之一［4-8］。在双曲集中有两个重要的研究对象：双曲周期点和双曲周期轨。这两个对象在双曲集的研究中扮演着很重要的角色，为许多双曲性的深入理解提供了两个很好的实例，是研究跟踪引理、横截同宿点理论、Ω-稳定性的基础。对双曲周期点大多数文献都给出了严格定义［1，3］，但是对于双曲周期轨大多数文献并没有直接给出严格的数学定义，而是将其嵌在双曲不变集的定义中［1，3］。由于双曲集定义的复杂性［1］，这极易导致很多学者将这两个概念混为一谈，这有失数学的严谨。实际上，它们定义的角度和反映的动力学目的是完全不同的，故有必要将这两个概念做一个详细的探究，阐明他们之间的区别与联系。本文将在双曲不变集的基础上将双曲周期轨的概念提炼出来，提出如下两个自然的问题：（1）双曲周期点形成的周期轨道是否为双曲集；（2）双曲周期点所形成轨道上的每一个点是否都是双曲的。据我们所知，目前文献中还未曾有关这两个问题的严格证明或说明。本文将严格证明上述两个问题的答案都是肯定的，从而彻底揭示双曲周期点与双曲周期轨之间的相互蕴含关系。

设X为m维紧致无边流形，具有黎曼度量，f∶X→X为一微分同胚。先给出几个相关概念和引理。

定义1［1］（双曲不动点） p为f的不动点，如果对切映射A=Df（p）∶TpX→TpX，存在TpX的一个直和分解：TpX=Es（p）⊕Eu（p），使得A在这个直和分解下保基点不变，即

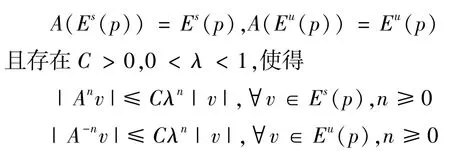
则称p为f的双曲不动点。

定义2［1］（双曲周期点） 设p为f的k周期点，fk（p）=p，fi（p）≠p，∀1≤i≤k-1。若p作为fk∶X→X的不动点为双曲的，则称p为f的双曲周期点。

下面给出双曲周期轨道的严格定义。

定义3（双曲周期轨） 若p为f的k周期点，则Orb（p）=｛p，f（p），…，fk-1（p）｝，记pi=fi（p），0≤i≤k，这里pk=p0。若对任意0≤i≤k-1，存在切空间TpiX处的直和分解Es（pi）⊕Eu（pi），使切映射满足保基点不变性

注由定义2和定义3可知，双曲周期点与双曲周期轨是两个完全不同的概念，k双曲周期点p是将p当成g=fk的不动点，该不动点为双曲的，换句话说，按照双曲不动点的定义1，即存在p点的切空间TpX的直和分解TpX=Es（p）⊕Eu（p），使得g=fm在这个分解下不变，且Dg（p）=Dfm（p）在Es（p）上一致扩张，在Eu（p）上一致压缩，而对轨道中其他k-1个点（即Orb（p0）｛p｝中的点）没有做任何要求。而双曲周期轨要求对轨道Orb（p0）中每一点都有切空间直和分解，使得切映射Df（x）（x∈Orb（p））在该直和分解上具有保基点不变性，且在每个子空间上分别具有保基点一致压缩和扩张。由此可知，双曲周期点看起来是一个“局部”的概念，而双曲周期轨道看起来是一个“整体”的概念，要求也更加苛刻。

引理1［1］设p为f的双曲不动点，对应于Df（p）的双曲分解TpX=Es（p）⊕Eu（p），则存在一个关于Es（p）⊕Eu（p）的乘积型范数｜·｜及一个常数0＜τ＜1（称为适配度），使得

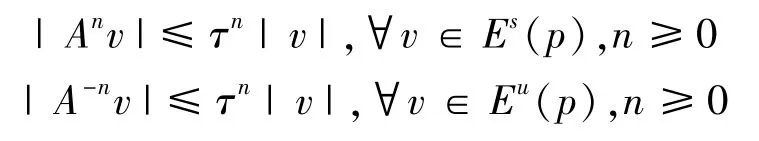
下面给出主要结果及其证明。

定理1X为m维紧致无边流形，具有黎曼度量，微分同胚f∶X→X，p0为f的双曲周期点的充分必要条件为Orb（p0）为双曲周期轨道。

证明（α）充分性的证明

设双曲周期轨道Orb（p0）=｛p0，p1，…，pk-1｝，这里pi=fi（p），1≤i≤k-1，fk（p）=p，Orb（p0）为有限个点组成，作为紧致空间的子集为紧致不变集，由双曲集的定义，对∀1≤i≤k-1，存在pi的切空间的直和分解Tpi=Es（pi）⊕Eu（pi），使得

且存在常数C＞0，0＜λ＜1，使得下式成立：

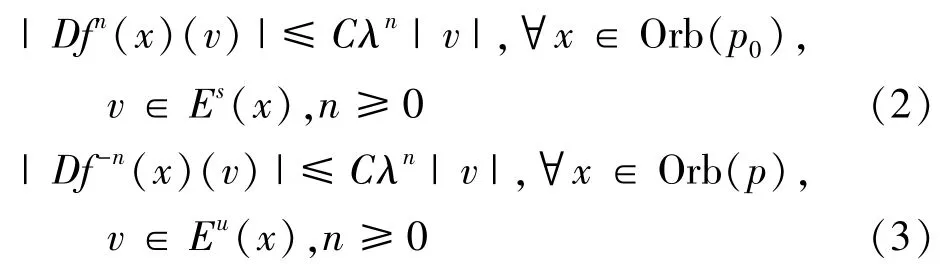
特别的，考虑微分同胚g=fk∶X→X，则p为g的不动点，且Dg（p）为Tp0到自身的线性映射。由复合同胚求导法则得

（b）必要性的证明

必要性的证明要复杂很多，分析如下。

分析p0为f的双曲周期点，设Orb（p0）=｛p0，p1，…，pk-1｝，要证明Orb（p0）为双曲周期轨道，根据定义，需要构造Orb（p0）中任意点处的切空间的直和分解，使得f的微分Df作用到分解上，保结构、保基点且一致压缩或发散。

第一步 构造保结构直和分解

由p0为f的双曲周期点，考虑微分同胚g= fk∶X→X，则p0为g的双曲不动点，所以存在p0处切空间的直和分解Tp0=Es（p0）⊕Eu（p0），满足

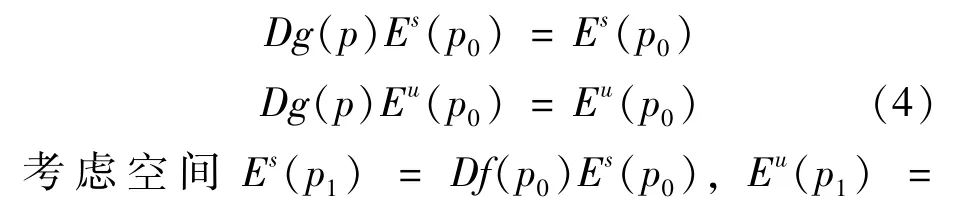
［1］张筑生.微分动力系统原理［M］.北京：科学出版社，1987：101-128，269-280.

［2］S.Smale.Differential Dynamical Systems［J］.Bull Amer Math Sci，1975，73：747-817.

［3］W.Stephen.Introduction to Applied Nonlinear Dynamical Systems and Chaos［M］.Second Edition.New York：Springer，2003：731-761.

［4］刘曾荣，曹永罗.双曲周期点的不变流形以及横截环［J］.应用数学学报，1993，16（3）：378-382.

［5］朱玉峻，王玲书，张金莲.具有双曲不变集系统的极限跟踪性［J］.数学年刊，2004，25A（5）：613-620.

［6］文兰，甘少波.阻碍集、拟双曲性与线性横截性［J］.北京大学学报（自然科学版），2006，42（1）：1-10.

［7］李怀彬，沈维孝.关于一维动力系统的非一致双曲性假设［J］.中国科学，2010，40（12）：1171-1186.

［8］L.G.Vikto，Z.G.Basak.Hyperbolic fixed points and periodic orbits of Hamiltonian diffeomorphisms［J］.Duke Math.J.，2014，163（3）：565-590.

An Equivalence Property Between Hyperbolic Periodic Point and Hyperbolic Periodic Orbit and Its Proof

WANG Lei1，2，YUAN Quan2
（1.Department of Mathematics and Physics，Hefei University，Hefei230601，China；
2.School of Mathematics and Statistics，Huazhong University of Science and Technology.Wuhan 430074，China）

We elaborate the similarities and differences between hyperbolic periodic pointand hyperbolic periodic orbit.Using the persisting property of dimension of differentialhomeomorphism and the derivative principle of composite homeomorphism，a rigorous proof is presented to imply themutual equivalence between them.

hyperbolic periodic point，hyperbolic periodic orbit，hyperbolic direct sum decomposition

O193

A

1007-4260（2014）03-0010-03

时间：2014-9-15 16：07 网络出版地址：http：//www.cnki.net/kcms/doi/10.13757/j.cnki.cn34-1150/n.2014.03.004.html

2014-06-19

国家自然科学基金（11302080），中国博士后科学基金（2013M530343）和合肥学院重点建设学科基金（14xk08）资助。

王磊，男，安徽阜阳人，华中科技大学在读博士，合肥学院数学与物理系教师，研究方向为微分动力系统。

袁泉，男，安徽合肥人，华中科技大学数学与统计学院博士后，研究方向为动力系统。