Gronwall-Bellman积分不等式在分数阶微分方程中的应用

李 琳，杨海洋，田 垒

（安庆师范学院数学与计算科学学院，安徽安庆 246133）

Gronwall-Bellman积分不等式在分数阶微分方程中的应用

李 琳，杨海洋，田 垒

（安庆师范学院数学与计算科学学院，安徽安庆 246133）

本文主要介绍了Gronwall-Bellman积分不等式及其推广形式在分数阶微分方程中的应用。利用Gronwall -Bellman积分不等式及其推广形式证明了分数阶微分方程解的唯一性，获得了一类分数阶时滞微分方程有限时间稳定的充分条件。

Gronwall-Bellman积分不等式；分数阶微分方程；初值问题；稳定性

分数微积分是任意（非整数）阶微分和积分的统称。近年来，分数微积分应用已经被越来越多的应用科学家及工程技术人员所青睐，其应用领域也越来越广泛。在许多种情况下，分数微积分比整数微积分更能准确地描述基本现象。相比于整数阶微积分而言，分数阶微积分对于反常扩散、电化学、粘弹性、控制科学、电磁理论等方面的应用是更好的理论工具。随着分数阶微积分的发展，分数阶微分方程模型也大量涌现，分数阶微分方程理论及应用的研究备受关注。Gronwall-Bellman积分不等式及其推广形式在在整数阶微分方程中对于稳定性、一致稳定性以及一致渐近稳定性的分析中具有广泛的应用［1-2］。本文主要利用Gronwall-Bellman积分不等式及Gronwall积分不等式的推广对分数阶微分方程解的唯一性进行证明，同时获得了一类分数阶时滞微分方程有限时间稳定的充分条件。

1 预备知识

定义1［3-4］对区间［α，b］上给定的函数f，函数f的q阶（q＞0）Riemann-Liouville分数阶微分定义如下：

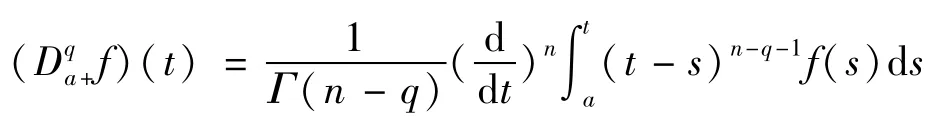
其中n=［q］+1，［q］表示q的整数部分，Γ（·）是伽马函数。

定义2［3-4］函数f∈L1（［α，b］，R+）的q∈R+阶Riemann-Liouville分数阶积分定义如下：

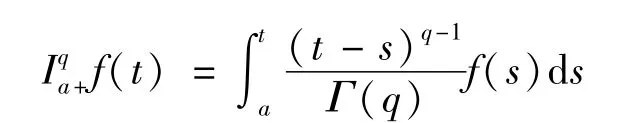
定义3［3-4］对区间［α，b］上给定的函数f，函数f的q阶（q→0）Caputo分数阶微分定义如下：

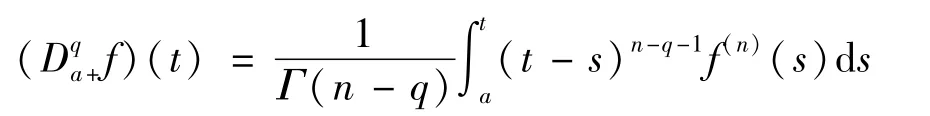
其中n=［q］+1，［q］表示q的整数部分。

引理1［5］（Gronwall不等式）设λ为非负数，f（t）和g（t）为在区间［α，b］上的连续非负函数，且满足不等式

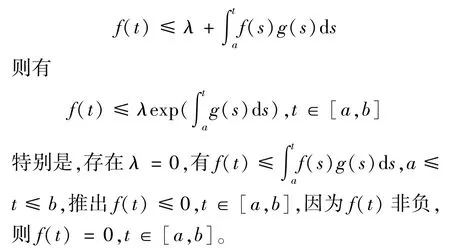
引理2［6］（Gronwall不等式的推广）令f（t），k（t）在［0，H］上是非负的且局部可积，其中H≤+∞，g（t）是定义在［0，H］上的非负非减的连续函数，且g（t）≤M（M是实数）。当q＞0时

2 Gronwall不等式及其推广在分数阶微分方程中的应用

首先利用Gronwall-Bellman积分不等式及其推广证明分数阶微分方程解的唯一性。

定理1已知

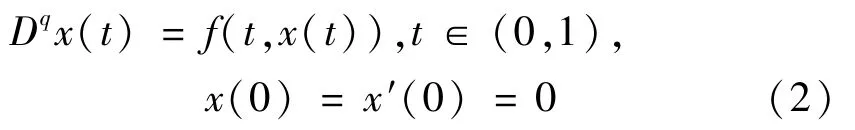
其中1＜q＜2，Dq是R-L分数阶导数，X=｛x（t）∶t2-αx（t）∈C［0，1］｝，x（t）∈X，f（t，x（t））∈C（［0，1］×R）且f满足Lipschitz条件，则初值问题（2）存在唯一解。

证明由文献［11］知，初值问题（2）的解存在，且初值问题（2）的等价积分方程为

证明根据分数阶0＜q＜1的性质，可以获得系统（5）的等价Volterra积分方程

注对于分数阶中立型微分差分方程

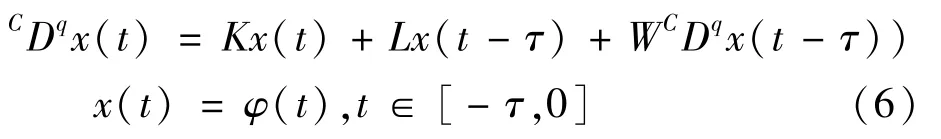
可借助于引理3获得有限时间稳定的充分性条件（参见［13］）。

［1］B.G.Pachpatte.Ineualities for differential and integral equations［M］.New York：Academic Press，1998.

［2］S.D.Sever.Some Gronwall type inequalities and applications［M］.Nova Science Pub Incorporated，2003.

［3］A.A.Kilbas，H.M.Srivastava，J.J.Trujillo.Theory and applications of fractional differential equations［M］.Elsevier Science B.V.，Amsterdam，The Netherlands，2006.

［4］I.Podlubny.Fractional differentialequation［M］.San Diego：Academic Press，1999.

［5］邹晓范，刘春妍.Gronwall积分不等式在微分方程中的应用［J］.佳木斯大学学报，2004，22（3）：417-419.

［6］H.Ye，J.Gao，Y.Ding.A generalized Gronwall inequality and its application to a fractional differential equation［J］.Journal of Mathematical Analysis and Applications，2007，328（2）：1075–1081.

［7］K.S.Miller，B.Ross.An introduction to the fractional calculus and fractional differential equations［J］.John Wiley&Sons，New York，NY，USA，1993.

［8］K.Diethelm.The analysis of fractional differential equations［J］.Springer，Berlin，Germany，2010.

［9］M.P.Lazarevi′c，A.M.Spasi′c.Finite-time stability analysis of fractional order time-delay systems：Gronwall's approach［J］.Mathematical and Computer Modelling，2009，49（3-4）：475–481.

［10］Abdulaziz Alofi，Jinde Cao，Ahmed Elaiw，Abdullah Al-Mazrooei1.Delay-dependent stability criterion of Caputo fractional neural networkswith distributed delay［J］.Discrete Dynamics in Nature and Society，2014，Article ID 529358：1-6.

［11］李秋萍，孙书荣，张萌，等.分数阶微分方程初值问题解的存在性与唯一性［J］.济南大学学报，2010，24（3）：312-315.

［12］俞成.分数阶微分方程的稳定性［D］.上海东华大学，2005.

［13］Denghao Pang，Wei Jiang.Finite-time stability of neutral fractional time-delay systems via generalized gronwalls inequality［J］.Abstractand Applied Analysis，2014，Article ID 610547：1-4.

Applicationsof Gronwall-Bellman Integral inequality in Fractional-Order Differential Equations

LILin，YANG Hai-yang，TIAN Lei
（School of Mathematics and Computation Science，Anqing Teachers College，Anqing 246133，China）

The applicationsof the Gronwall-Bellman integral inequality and itsextended form in the fractional-order differential equation aremainly introduced in this paper.Taking advantage of Gronwall-Bellman integral inequality and its extended form，we prove the uniqueness of the fractional-order differential equations and obtain the sufficient conditions of finite-time stability for a class of fractional-order differential equation with delay.

Gronwall-Bellman integral inequality，fractional-order differential equations，initial value problems，stability

O175.1

A

1007-4260（2014）03-0013-04

时间：2014-9-15 16：07 网络出版地址：http：//www.cnki.net/kcms/doi/10.13757/j.cnki.cn34-1150/n.2014.03.005.html

2014-04-19

安徽省高等学校省级自然科学研究基金项目（KJ2011A197，KJ2013Z186）资助。

李琳，女，安徽阜阳人，安庆师范学院数学与计算科学学院硕士研究生，专业方向为分数阶微分方程。