政府税收行为与休闲体育产业的二层规划模型

侯阔林

（黎明职业大学公共教学部，福建泉州 362000）

政府税收行为与休闲体育产业的二层规划模型

侯阔林

（黎明职业大学公共教学部，福建泉州 362000）

政府税收政策影响企业的投资策略，为提升我国休闲体育产业的发展规模和竞争力，需研究政府最优税收策略与企业投资策略的数学模型。分析产业背景并提炼关键决策变量，建立了二层规划模型。在政府确定税收目标及休闲体育产业的发展目标后，设计了一个确定最优税率的模糊交互式算法，同时也可保证企业根据政府的最优税率来确定最优投资方案以最大化其期望效益。实际案列验证了模型的合理性。

最优化方法；税收策略；休闲体育产业；二层规划

休闲体育产业是一种节能环保的朝阳产业，而我国休闲体育产业规模小、科技含量低、竞争力不强，与其他已发展行业相比，政府的税收政策对其发展的影响尤其重要。为推动体育产业的发展，政府相继出台了一些法规，如《全民健身计划》、《全民健身条例》、《国务院办公厅关于加快发展体育产业的指导意见》、《体育事业发展十二五规划》等［1］。

许多学者认为，政府能够和应该在财税政策方面扶持和引导休闲体育产业发展壮大［2-4］。目前的研究成果大多作定性描述、理论分析，也有学者使用统计分析的方法做实证研究［4］。遗憾的是，这些研究无法回答各种税率是多少时，能有效地激励企业扩大规模、增加科技研发投入以打造最具有竞争力的休闲体育产业。如果建立一种成熟的数学模型来解决这个问题，势必在理论研究上能有所推进。

政府可以通过调整税率影响企业行为以达到做大、做强体育产业和满足人们休闲娱乐、体育锻炼需求等目标；企业根据政府的税收政策做出反应，适度调整投资方向和投资额，以获取最大利润与发展潜力。如果政府将制定税率作为决策变量，将提高企业的竞争力作为目标，引导企业合理投资；而企业决策如何投资以获取最大利润，则这可用一个二层规划模型来描述二者的博弈关系。二层规划是具有二层结构的数学模型，不同层次具有不同的、也许是相互冲突的目标函数，且下层规划以上层规划的决策变量为参数，其决策变量（或通过目标函数值）又影响到上层规划问题的求解［5-6］，在电力市场、供应链管理和系统工程等领域应用广泛。本文选政府作上层决策者（leader），决策目标是F（x，y），决策变量集是x，受到集值函数f（x，y）≤0的约束；企业作下层决策者（follower），决策目标是G（x，y），决策变量集是y，受到集值函数g（x，y）≤0的约束。在建立模型时，将对模型（1）的变量和函数具体化。

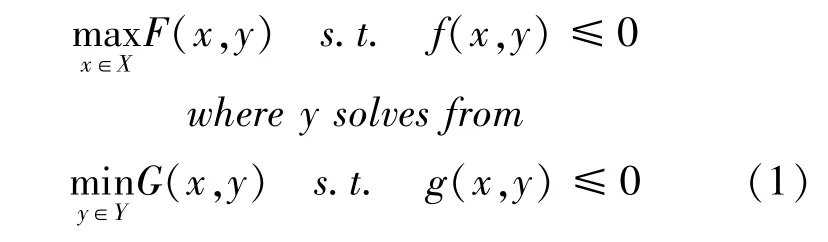
1 政府的税收政策

政府财政收入的主要来源是税收，而我国体育产业对税收的贡献率不足1%，约为美国的1/10、发达国家平均贡献率的1/4，主要原因是我国体育产业弱小［2］。如果政府适当调整税收政策，我国的休闲体育产业是能够发展壮大的，并对经济发展、增加就业、提高国民身体素质甚至促进社会稳定起到良好地作用。现行的税率标准如表1所示。

表1 现行体育与税收政策的征税内容与相关优惠政策［7］

税收研究是一件很复杂的工作，税种繁多，相关免税、减税和抵税的政策条款也很多。为研究方便和得出简明的、具有普遍性的结论，作如下假设：

（1）假设对企业发展产生重要影响的税种为营业税、增值税、所得税和房产税，且缴税期为1年；

（2）假设企业的营业额为企业当期的销售额；

（3）假设增值税最终转嫁到消费者承担；

（4）假设休闲体育产业的规模与场地面积成正比；

（5）假设市场需求是一个随机变量，并且是价格的减函数；

一些研究成果［8-12］揭示，营业税、增值税、企业所得税、房产税对企业的税收负担起决定作用。鉴于厦漳泉三地休闲体育产业发展具有代表性，为提取恰当的变量x，y，我们对该地区休闲体育产业做了具有针对性的调研，结果表明增值税、营业税、房产税、企业所得税是主要的税收负担。另外，为鼓励产业发展，政府规定企业投入经费作科研、技术创新可以按一定比例抵营业税。为了准确地描述政府1年的税收收入，需引入以下符号：

B 企业的营业额，用于计算营业税；

V 企业“当期销项税额”减去“当期进项税额”，用于计算增值税；

I 企业所得额，用于计算企业所得税；

t1，t2，t3依次为营业税、增值税、企业收入所得税的税率；

H 企业的土地使用面积，单位：平方米；

t4每平方米土地的适用税额；

R 企业在当期的科技研发投入经费；

k 科技研发经费可以用于抵税的比例；

A 企业的广告投资额；

S 企业用于扩大规模的投资额，设与场地面积H有关，S=k0H，k0为常系数。

政府的决策目标是提升企业的竞争力和生产效率，这与企业的科技研发投入、广告宣传投入和扩大生产规模投入有关。事实上，对于政府来讲，竞争力和生产效率具体表现为该产业的生产总值。衡量生产总值一般用柯布·道格拉斯生产函数［12］，其基本形式为：

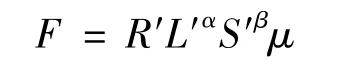
其中R′是综合技术水平，L′是劳动力数（单位：人），S′是投入的资本，一般指固定资产（单位：万元）。运用柯布·道格拉斯函数取对数之后可线性化，计算方便，并且在各生产部门取得了成功应用。用来分析休闲体育产业的发展，能够得出各要素投入对产出的贡献率、规模收益和其他系列问题。陈虹霁等［12］使用柯布·道格拉斯函数研究电力、电气、纺织、化学、交通、石油、设备等各行业的技术、资本和劳动力方面的投入与生产效率的关系：

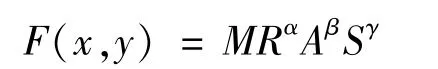
其中x表示政府的决策变量，y表示企业的决策变量。以后，F（x，y）简记为F。M为常系数，α，β，γ代表各对应项投入的产出弹性。

政府通过税率t1，t2，t3的调整，希望能够增强企业的竞争力，提高其生产效率，考虑到文献［12］的结论比较成熟，并且产出弹性有详实的调查数据可以采用。我们的目标函数将借鉴F（x，y）= MRαAβSγ的形式。考虑到政府还需要引导企业发展以满足人们日益增长的休闲体育活动，降低休闲体育产品的价格。基于此，建立目标函数

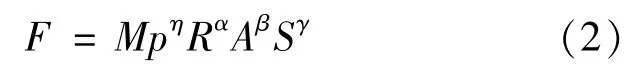
其中p表示价格，M为实系数，称（2）为企业的竞争力函数。

另外，政府的决策受到一些条件约束，比如其税收要能够维持正常运转，而当期税收为Bt1+Vt2+It3+Ht4-kR，因此，要求Bt1+Vt2+It3+Ht4-kR≥T0等。

2 企业的行为

当前，休闲体育市场供不应求，部分企业不注重服务质量和科技含量的提升，盲目扩大规模、牺牲质量降低成本或者提高价格谋取暴利。长此以往，休闲体育产业难以健康发展。解决这个问题，需要摸清现状。从市场需求来看，厦漳泉三地约89.1%的消费者年度休闲体育消费在3 000元左右。79%的场所客流量在每天100人左右，目前休闲体育运动每次的平均收费为238元，消费者认为136元是合理的。从企业方面看，68.9%的企业盈利30%左右，大部分中小企业每年投资在100万上下，广告投入约10万，休闲体育服务业科技研发投入较少，只有休闲体育用品产业科研投资额在20万左右。

一些有远见卓识的企业家不仅看到眼前的利润，也会重视企业的发展前景。加大科技研发投入，优化企业场地的自然与人文环境将有利于企业的发展壮大，提高企业的竞争力，这也是政府扶持休闲体育产业的目标之一。下面引入一些符号：

S 企业用于扩大规模的投资额，设与场地面积H有关，S=k0H；

R 企业的科技研发投资额；

A 广告投入投资额；

p 企业对产品的定价；

Q 客容量；

x 市场需求x=α+bp+ε；

d 将未来资产折现为现值的贴现率。

2.1 企业的销售收入与企业成本

不考虑科技研发带来的加成效果时，企业的销售收入为：

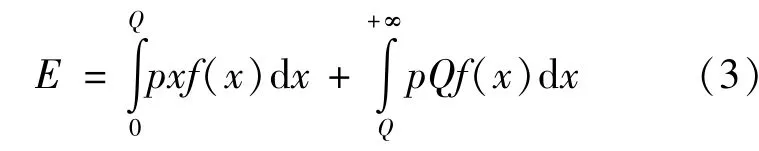
企业的成本：S+R+A+Bt1+Vt2+It3+Ht4-kR，其中第一项为扩大规模的成本，第二项是科技研发投入成本，第三项是广告宣传成本，第四项至第七项为税务成本，第八项是由科技投入引起的抵税。

2.2市场需求与价格的关系

经济学上，市场需求是价格的减函数，有线性函数y=α-bp（其中α，b是常数）、幂函数形式如平方形式y=α-bp2，指数形式如y=αe-bp等。具体的取值因从事的行业各异，比如体育用品制造业、休闲赛事产业、休闲健身产业和休闲旅游产业是不同的。即使是同一行业，设备精良、服务质量高的企业同一价格下需求也较高。本文选取最为常用的线性形式y=α-bp。

2.3 广告宣传对企业产出的影响

广告信息会对消费者产生说服作用，最终影响市场需求，但是，并非投入越高回报越大。不同的行业和不同的企业规模，其合理的广告投资额度不同。并且，不同的广告方式和营销方式等相关因素也会对广告效应产生影响。广告投资回报率是一个复杂的问题，不是本文研究的主题，不做深入和细致的分析。从调查结果来看，广告宣传对企业的影响主要体现在市场需求方面。对市场需求的影响为

其中λ为广告对销售量的提高因子，其取值是广告投入的幂函数，比如γ=-1.000 011 79A2+ 0.006 87A+1.02。

2.4 科技研发对企业产出的影响

科技对企业发展的贡献具有持续性，这种持续可以用永续存盘模型来度量，即Tn=Rn+δTn-1，其中δ为折旧率，Tn表示技术存量。

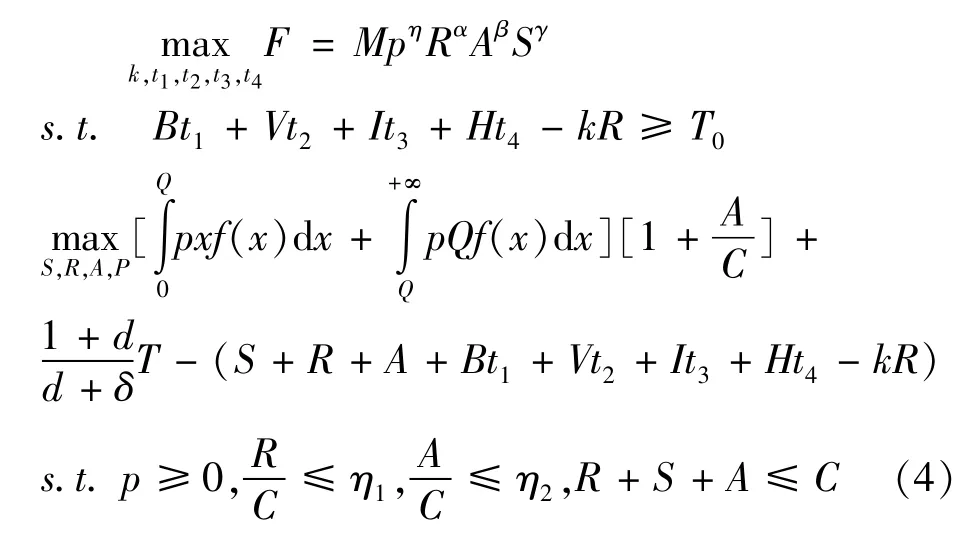
3 二层规划模型

其中，T是科技研发投入带来第一年的产出，Q和H是S的函数，一般是增函数，在不同的地域和企业稍有不同。这里客容量和价格是以年为单位的，分析具体问题时按天计算更恰当，建议按1年365天折算成1年。从约数条件可以看出，科技投入和广告投入受到参数η1，η2的限制。

营业额是销售收入减去销售成本：

模型（4）是一个非线性二层规划问题，传统上的分支定界法、k次最好算法或罚函数方法均不适合求解该问题。至于能否通过KKT方法或者转化为MPEC问题（Mathematical Program with Equilibrium Constraints，简称MPEC）求解，需要作如下分析。

定理2函数F=MpηRαAβSγ是连续可微的。

证明对（2）式F=MpηRαAβSγ两边同时取对数可得

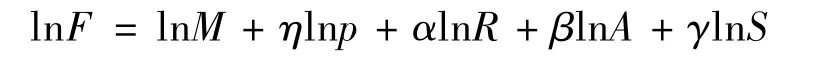
再两边同时关于p求偏导，得竞争力函数对价格的偏导数为

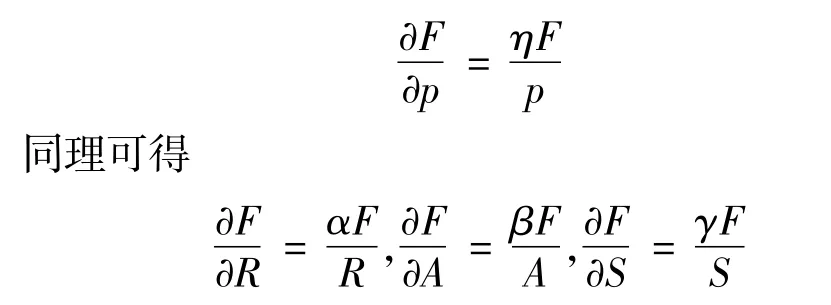
其中α，β，γ，η都是常数，显然函数F=MpηRαAβSγ是连续可微的。

定理3下层规划问题的约束区域是凸集。

证明从条件可知R+S+A≤C，它们围成的是一个闭半空间，根据优化理论知闭半空间是凸集。

定理4目标函数G（S，R，A，p）是连续可微的，但是不具备凸性。

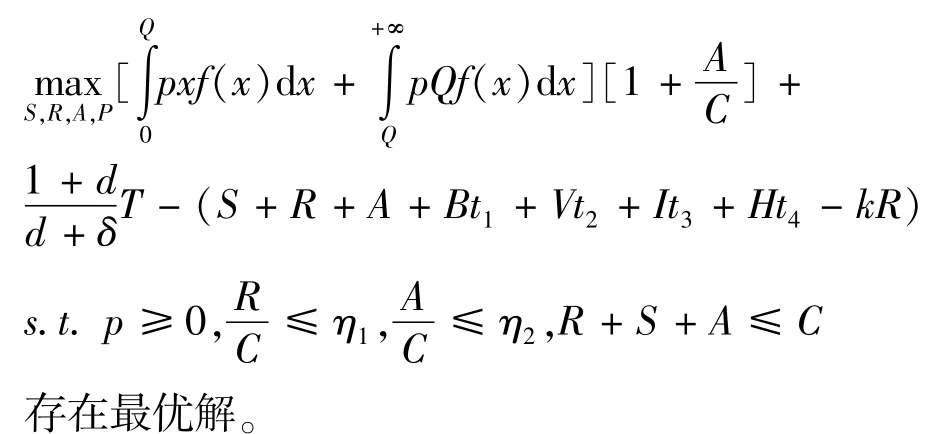
可见T″（R）决定了函数G（S，R，A，p）对变量R的凸性，而函数对变量S和p不具备凸性。

考虑到G（S，R，A，p）不具备凸性，不存在解析算法求解二层规划问题（4），如果其下层规划的解存在，可以考虑使用模糊交互式算法［6］求解之。

定理5如果定义了价格p的上限，则下层规划问题

证明从定理4可知，函数G（S，R，A，p）是连续的，从定理3可知下层规划问题的约束区域是凸集，若再限制0≤p≤P0，约束区域为闭凸集。连续函数在闭凸集上一定存在最大值和最小值。故下层规划存在最优解。

4 算法与案例

4.1 算法

二层规划问题是一个NP-hard问题，其求解方法目前主要有以下几类：极点搜索方法、罚函数方法、分枝定界法和进化逼近方法等。如果随机变量为连续型，则问题（4）下层的积分较为复杂，可以采用如下离散逼近方法将其转为确定性的二层规划问题。

设随机变量x的支撑域为［A，B］。对充分大的正整数K，在此区间内任意插入K-1个分点，将其分为K个子区间［Aj，Bj］，其长度Δj=Bj-Aj（j= 1，…，K）。记x落在子区间［Aj，Bj］的概率为μj= f（xj）Δj（j=1，…，K），其中xj为子区间［Aj，Bj］上的任意一点。

由于企业和政府所追求的利益有一定的冲突，表现为一种不合作的对策行为。同时，他们的决策相互影响和依赖，也有一定程度的合作。他们对彼此的信息是不完全的、模糊的，在此种条件下寻求自己的最优解（或满意解），因而他们有各自的模糊目标函数。假设我们考虑的二层规划为

X为相关空间上的有界闭凸子集。设函数-F，-G的隶属函数分别为μ（-F）和μ（-G），最小可能接受（满意）值分别为θ1和θ2（0≤θ1，θ2≤1），即μ（-F）≥θ1且μ（-G）≥θ2。在没有任何信息情况下，决策者们要作出自己的最小可接受水平同时又被其他决策者所接受是比较困难的。我们可以利用模糊决策方法，即所有决策者的最小满意水平中的最大者，从而得到一个适当的最小可接受水平。虽然在上层决策者在决策过程中占主导地位，但我们应公平对待下层决策者。为此利用最小可接受水平θ1求解如下规划问题

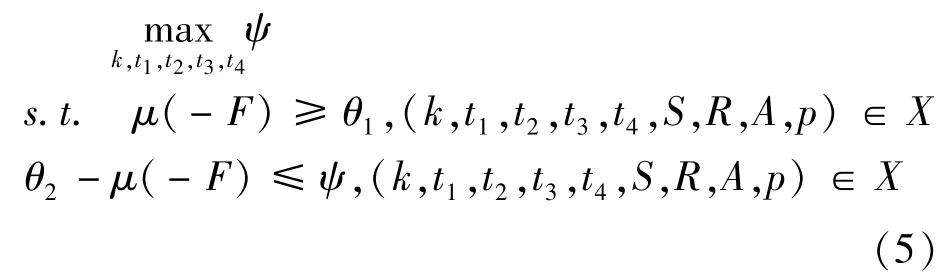
得到下层问题的临时满意解。其中ψ是一个参变量。若解不存在，则其约束不相容，因而需要调整上层决策者的最小接受水平。若解存在，根据各个决策者的满意度的比值（均衡满意度，见（6）式）不断调整他们的最小可能接受水平值，最终得到一个大家都能接受的满意解。

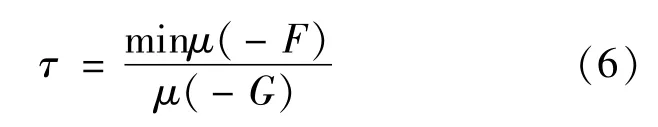
上层决策者以此判断是否改变自己的最小可接受水平值。若ξ＜1，则上层决策者为了增加自己的决策力（即增加最小可能接受值θ1），需要对下层决策者的决策力进行一定的限制（即减小最小可能接受值θ2）；不然，需要减小最小可能接受值θ1而增加最小可能接受值θ2。至此，有如下交互式模糊决策算法

Step 1 给出上下层目标函数-F（k，t1，t2，t3，t4，S，R，A，p），-G（k，t1，t2，t3，t4，S，R，A，p）的隶属函数μ（-F）和μ（-G），以及最小可能接受（满意）值θ1和θ2，允许误差。

Step 2 求解规划（5）。若其解不存在则调整上层决策者的最小接受水平θ1，重新求解规划（5）的解

4.2 案例

厦漳泉地区的休闲体育具有代表性：其旅游产业得天独厚；拥有大量的体育训练基地，承办了一些国际、国内赛事；休闲体育用品产业国内领先、实力雄厚、竞争力强，其中泉州的晋江市被誉为品牌之都。水上乐园、垂钓园、高尔夫球场、保龄球馆、台球房、轮滑场、SPA健身休闲会所特别是健身俱乐部如雨后春笋。我们设计问卷调查企业领导、消费者和行业协会人员。收回有效卷282份。显示厦漳泉三地在2012年约有休闲体育用品企业5 000余家，年产值约500亿，就业人数约50万人。壮大体育产业规模、提升体育产业竞争力，需要政府税收优惠政策的扶持。泉州市某健身俱乐部预算今年投资总额为400万元，工资和办公费用等开支为100万元，用于科技研发的投资额不超过总投资额的30%，广告投资不超过10%。不妨设扩大规模的投资每增加1万元增加1个日客容量，由于租房的原因房产税忽略不计，市场调查显示每天约300人次顾客。对于每天的需求函数y=α-bp，取α=320，b=8 000，ε∈［-10，10］，单位是万元。1年按365天计算，不妨设每天客流量相同。政府从该企业最少需要获得10万元的税收。问政府应如何对税率和税收优惠作出决策能最大化企业竞争力？企业应如何决策能获得最大的期望利润？

针对上述问题，易知投资限制参数η1=0.3，η1=0.1，为简便起见，取Q=［S］。

市场需求x=320-8 000p+ε，ε∈［-10，10］。鉴于文献［12］，本文选取α=0.86，β=0.32，γ=0.27。对于贴现率取d=3.2%，δ=8%，则为科技研发的第一年收入。

在现行的税率和科技优惠条件下，企业的最优反应是：

K T1 T2 T3竞争力S R A p利润1 0.2 0.17 0.25 1 406.3 273.0 95.1 31.9 0.016 89.88

但是政府为了提高一个行业的竞争力F= 10-4p-0.62R0.86A0.32S0.27，很显然需要提高R和A的值。政府通过变动科技投入优惠k和营业税、增值税、企业收入所得税的税率：t1，t2，t3，引导企业增加科技投入和广告宣传投入R，A。计算表明，科技投入对参数k是敏感的：

K T1 T2 T3竞争力S R A p利润1.5 0.2 0.17 0.25 1 349.0 251.5 120 28.5 0.002 75.97

然而，为了满足人民日益增长的物质文化需求，政府希望降低休闲体育运动的产品价格，这需要降低税率t1，t2，t3，例如降低到如下数值，企业的最优反应为：

K T1 T2 T3竞争力S R A p利润1.67 0.1 0.07 0.12 1941 261.3 112.3 26.4 0.018 89.66

以上算例展示了政府和企业的交互关系，事实上，可以使用模糊交互式算法，计算出二层规划的最优解：

K T1 T2 T3竞争力S R A p利润1.67 0.12 0.03 0.05 2 005.8 245.2 118.3 36.5 0.015 114.47

结果表明，使用二层规划模型研究该问题，有助于为政府和企业作出科学决策，能够提升休闲体育产业的竞争力，满足政府税收和提高人民生活质量的要求。也能够降低企业的税务成本，提升企业的科技水平，增加利润。

5 结束语

研究政府行为对休闲体育产业的影响实际价值很高，该问题是一个复杂性系统。将政府行为抽象为税率和税收优惠，将企业行为简化为扩大规模投资、科技研发投资和广告投入与定价。在满足既定约束的前提下，政府最大化产业竞争力，企业最大化自己的利润，而其决策是交互影响的。建立二层规划模型解决休闲体育产业链的问题属首次尝试，还可以向多个企业、更细致的策略等方向拓展研究。

［1］唐广宁.我国体育产业的SWOT分析及其发展战略研究［J］.沈阳体育学院学报，2012（1）：11-14.

［2］曾广新.关于发展我国体育产业的思考［N］.光明日报，2008 -09-17.

［3］杨京钟，吕庆华，易剑东.中国体育产业发展的税后激励政策研究［J］.北京体育大学学报，2011（3）：5-8.

［4］杨倩.基于统计数据的我国体育产业结构及其产出分析［J］.天津体育大学学报，2012（1）：27-30.

［5］S.Dempe.Annotated bibliography on bilevel programming and mathematical programswith equilibrium constraints［J］.Optimization，2003，52：333-359.

［6］王广民，万仲平，王先甲.二层规划综述［J］.数学进展，2007，36（6）：513-529.

［7］杨京钟.税务流程与纳税申报［M］.福建：厦门大学出版社，2010.

［8］王德平.体育用品产业创新能力发展策略［J］.体育科学研究，2010，14（4）：11-16.

［9］王隆华.福建体育旅游产业跨越发展的战略选择［J］.南京体育学院学报，2012（1）：84-88.

［10］余政宣.福建海西体育旅游经济圈的构建与价值［J］.三峡大学学报，2010（12）：106-107.

［11］林少琴.从闽台两地体育赛事旅游的发展看两岸的交流与合作［J］.广州体育学院学报，2011（2）：38-42.

［12］吴瑞溢，杨京钟.泉州休闲体育业税收优惠激励的灰色关联评价［J］.黎明职业大学学报，2013（3）：31-35.

［13］陈虹霁，陈德智.企业研发投入与生产效率［J］.科技管理研究，2012（11）：99-103.

A Bi-level Programming Modelof Government Tax Behavior and Leisure Sports Industry

HOU Kuo-lin
（Faculty of Foundational Education，LiMing Vocational University，Quanzhou，Fujian，362000，China）

Government tax policies affect leisure sports industry investment strategy.To enhance the leisure sports industry's development and competitiveness，we study themathematicalmodel to determine the optimal government tax policies and the investment strategy of enterprises.By analysis of previous studies results，and refining the key decision variables，we establish a bilevel programmingmodel.After the government determined taxation revenue target and leisure sports industry development goals，the result of numerical calculation reveals optimal tax rate.The firm decides optimal capital projectmaximize the expected profit.

optimization method，tax policy，leisure sports industry，bi-level programming

O227；F812.42

A

1007-4260（2014）03-0022-06

时间：2014-9-15 16：07 网络出版地址：http：//www.cnki.net/kcms/doi/10.13757/j.cnki.cn34-1150/n.2014.03.007.html

2014-04-25

泉州市哲学社会科学研究2013年规划项目（2013Z03）资助。

侯阔林，男，安徽萧县人，硕士，黎明职业大学公共教学部讲师，研究方向为最优化方法及其应用。