带有惯性敏感元件的新型陀螺测试转台系统控制器设计

杨亚非，张 翔

（哈尔滨工业大学 控制与仿真中心，哈尔滨 150080）

带有惯性敏感元件的新型陀螺测试转台系统控制器设计

杨亚非，张 翔

（哈尔滨工业大学 控制与仿真中心，哈尔滨 150080）

传统原理的陀螺测试转台使用测角元件测量转台的角速率，其精度与所选的角度（或时间）间隔关系极大，即使综合使用各种控制方法也难以达到理想的速率精度和速率平稳性。提出一种新的测速原理，将惯性敏感元件引入转台测试系统测量瞬时角速率，瞬时速率能够很好地反映速率精度和速率平稳性，通过反馈与控制瞬时角速率信息提高转台的速率精度和速率平稳性。探讨了带有惯性敏感元件的新型转台的控制系统组成，进行控制系统设计时，将闭环系统按功能划分成测量回路和稳定回路，并运用数字控制解决控制器综合问题，使用Matlab软件分析系统主要变量响应过程。最后，由控制器设计过程和所得模型分析结果证实，相对传统转台，新型转台的数字控制系统具有较高鲁棒性，响应时间缩短为0.15 s，更适宜于陀螺仪表的动态测试。

陀螺仪表；瞬时角速率；速率精度；速率平稳性；控制器综合

在现有技术条件下，提高陀螺测试转台的精度是提高陀螺仪精度的有效途径。速率精度和速率平稳性是转台最重要的性能指标。目前，现有转台通常使用各种测角元件测得转台的平均角速率信息，综合各种控制方法补偿有害因素，提高转台的速率精度和速率平稳性指标，然而，测得的平均速率信息并不是瞬时角速率，所以不能真正反映这两项指标的好坏。传统转台还有一大弊端，那就是采用大转动惯量的主轴来提高速率平稳性，这样不仅增加了转台功耗，也使其加减速性能变差，无法达到速率的快速稳定[1]。

本文在借鉴国外先进测试转台工作原理的基础上，提出将高精度惯性敏感元件引入到转台测试系统中测量转台瞬时角速率。在进行系统回路控制器设计时，按照功能原理将转台控制回路分为测量回路与稳定回路分别进行控制器综合设计。最后利用Matlab软件对所得结果进行仿真验证，并对所得结果进行分析。

1 传统转台的控制系统

转台是一个典型的伺服系统，为陀螺仪表测试提供速率基准。按照反馈信息划分，常见的有位置反馈和速度反馈系统，带有位置和速度反馈的系统结构框示于图 1。带有速度反馈和纯积分环节的的伺服系统可以较好的抑制摩擦力矩对转动的影响，有效的改善系统的低速性能[2]。转台转动的加速度信息也可以用于反馈，尤其是当转台低速转动，加速度变化较明显时，加速度反馈可以有效抑制转台轴系的干扰力矩，减小低速状态下速率的波动[3]。

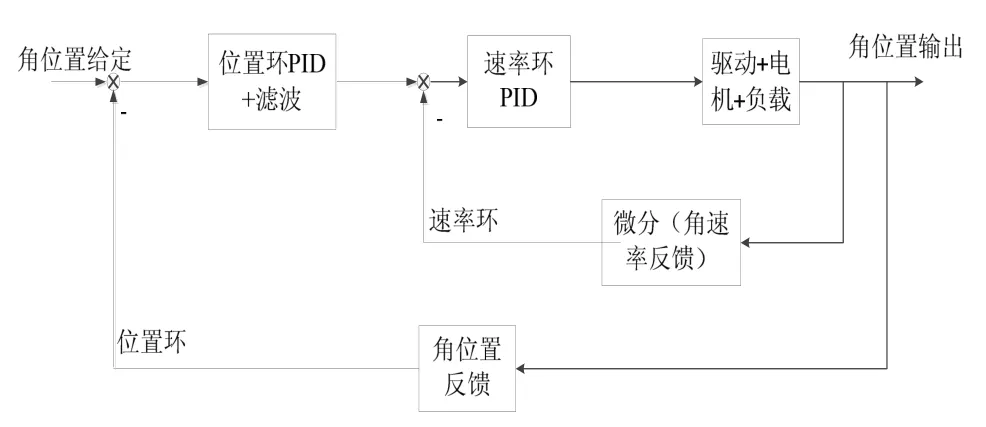
图1 带有位置和速度反馈的系统结构框图Fig.1 Structural scheme of system with position and rate feedback

转台的控制主要采用传统PID控制和包括鲁棒重复控制、自适应控制等在内的先进控制算法。传统PID控制是最成熟、实际使用最广泛的控制方法，优点是简单易行、调节方便，且满足绝大多数控制系统的要求[4]，缺点是参数调节依赖于人为经验。PID控制后又发展衍生出数字PID[5]等控制算法，可以满足系统对稳定性能和动态性能的要求。先进控制算法研究较为广泛，众所周知，影响转台速率精度和速率平稳性的主要因素包括轴系的摩擦力矩、驱动电机的换向力矩和齿槽力矩、测量反馈元件的周期性误差以及负载的不平衡力矩等。各种因素对转台转动的影响不尽相同，以转台驱动电机的换向力矩为例，由其产生的机理可知，其是转台角位置的函数，因此为了抑制和消除电磁干扰力矩，可以使用混合鲁棒重复重复控制、自适应逆控制等先进控制方法。

2 新型转台的控制系统系统组成

基于以上分析，尽管传统转台采用各种控制方式以使测试转台系统达到最佳的控制效果，但是由于传统转台使用的测角元件是光电编码器、旋转变压器或感应同步器等类型的测角元件，严格意义上说，测量得到的是某一时间间隔或角度间隔内的平均角速率，而不是转台的瞬时角速率信息，而只有瞬时角速率才真正反映转台的速率精度和速率平稳性。因此，考虑将高精度惯性敏感元件引入到转台系统中测量平台瞬时角速率。通过对瞬时速率进行测量、反馈和控制达到提高转台速率精度和速率平稳性的目的[6-8]。

新型转台在放置被测仪器的平台下方增加一个与主轴相连的圆盘，用于安装引入的惯性敏感元件[9]。角速度传感器固定在圆盘正中，其敏感轴沿主轴方向，用于测量转台低速转动时的瞬时角速率。在圆盘边缘对称固定三个向心加速度计和三个切向加速度计，每两个同类加速度计的安装半径呈120°分布，分别用于测量向心加速度和切向加速度，以此得出转台转动的瞬时角速率和角加速度。

综合考虑引入的角速度传感器的动态误差以及加速度计的测量范围和灵敏阈，确定测试转台系统可以工作在低速模式和高速模式。低速模式的速率范围为0.01～30 (°)/s，系统的惯性敏感元件为角速度传感器和切向加速度计；高速模式的速率范围为30～1200 (°)/s，系统的惯性敏感元件为向心加速度计和切向加速度计。

根据以上的功能原理，并且结合国外研制的陀螺转台，得出如图2所示的低速模式下系统结构框图。图中包含的符号意义为：分别是干扰力矩、平台稳定轴的角速度和角速度传感器的进动角速度；Mω,Mε是沿测量元件敏感轴产生的陀螺力矩；Mdm是驱动电机力矩，是控制力矩；β,βτ,βC以及是敏感元件进动角以及简化为这些角度的噪声干扰；uω既是敏感元件的信号uAVS的在低速模式下数字表示，也是加速度计1c～3c的信号uc的在高速模式下数字表示的平方根之和，uε是加速度计1τ～ 3τ的信号uτ的数字表示的总和。

根据实现功能的不同，并且从便于控制器设计出发，将转台闭合回路划分成测量回路和稳定回路两个部分。测量回路用于测量角速度传感器和加速度计的输出信息，将输出信息一方面用于反馈控制，传递给控制器形成控制作用，另一方面闭环测量回路整体作为稳定回路的一个功能元件，将信息提供给稳定回路用于保证转台系统的稳定性。由于低速模式和高速模式的分析思路基本相同，只是系统中惯性敏感元件不同，因此本文以下的分析均以低速模式为例进行介绍。

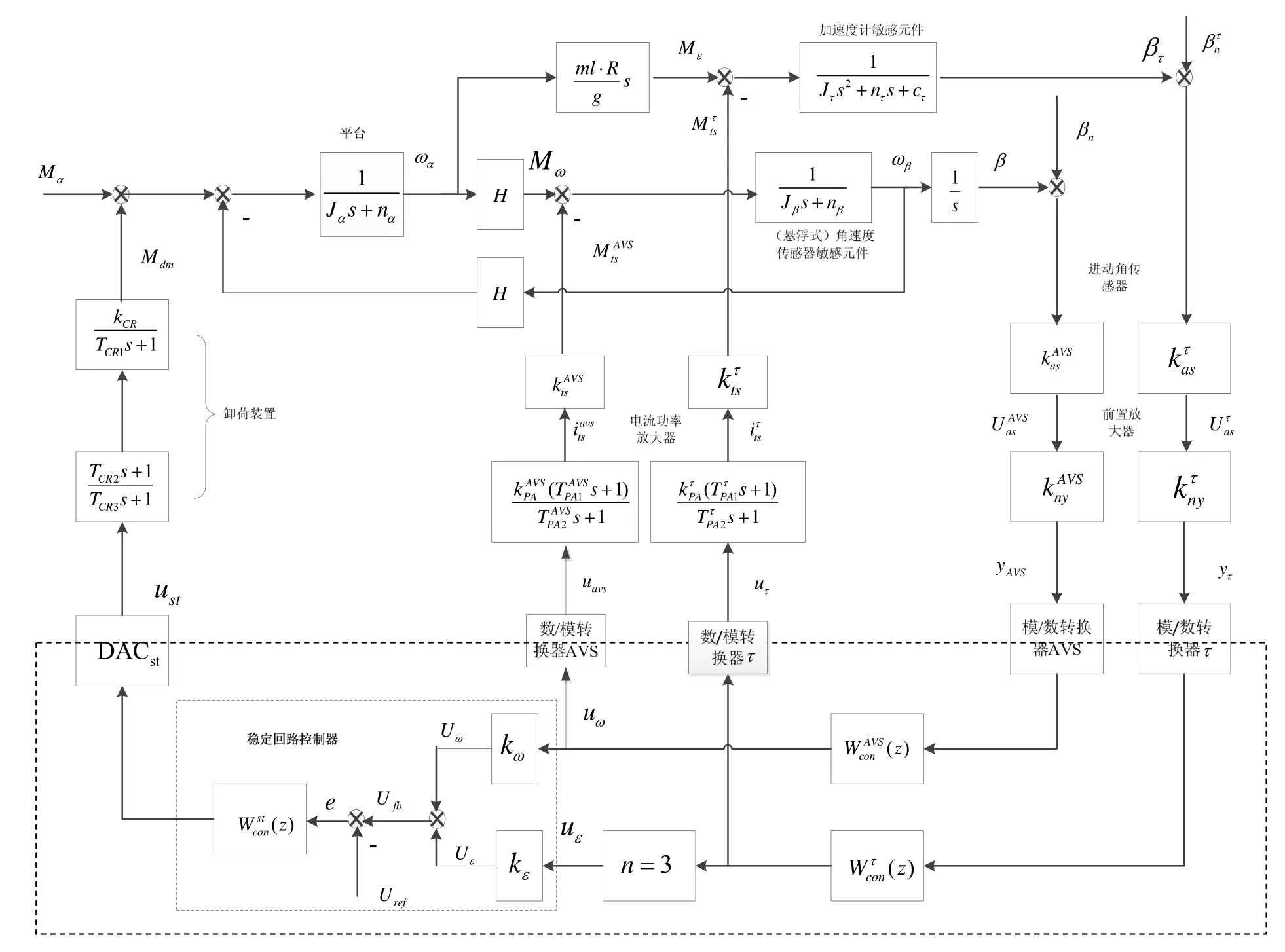
图2 低速模式下测试转台的控制系统结构框图Fig.2 Structural diagram of the test turntable’s control system in the low-rate mode

3 测量回路控制器设计

由于传统的模拟控制无法在线重调整参数，无法根据任意定律测量和指定转台角速度，而数字控制具有控制算法灵活，便于在线修改控制参数和可靠性高的优点，因此提出用数字控制代替模拟控制，解决控制器的综合和设计问题[10]。测量回路控制器的设计步骤如下：

1）根据结构原理图，选定状态变量构建角速度传感器回路对象的微分方程。

由图2得，角速度传感器测量回路的被控对象为角速度传感器和前置放大器，对象的控制输入是数/模转换器的输出信号uavs，被测输出是前置放大器的输出yAVS。取状态变量为yAVS,β,和辅助变量，得到角速度传感器回路的状态方程：

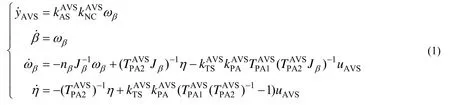
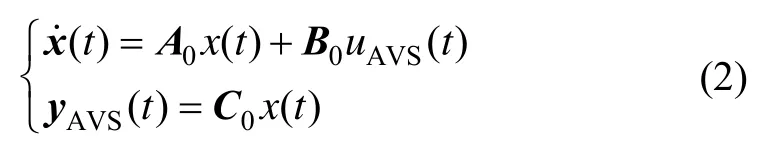
2）考虑量化频率，将建立的状态空间模型转化为离散模型。

在t=ih时刻，由模/数转换器对被测输出进行转换，h是离散化周期。转台系统中频率最高的元件是加速度计，将系统时钟频率选取为比加速度计闭环回路的期望通频带上限大得多的值，定为10 kHz。选取离散化周期时，保证离散化后系统仍是稳定的，鉴于确定好系统的时钟频率为 10 kHz，故取。

由已建立好的数学模型(2)，考虑一个周期内的控制延迟，将其离散化得到：

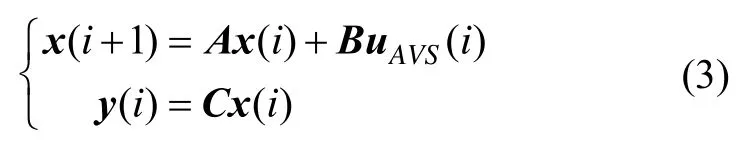
3）根据延迟模型，引入离散积分器以实现无静差，扩展得到新的离散模型。

增加带有系数φ的离散积分器为。由于控制延迟，引入辅助变量，并将其作为控制器。引入扩展状态向量以及新的被测输出，根据式(3)得出新的离散系统：

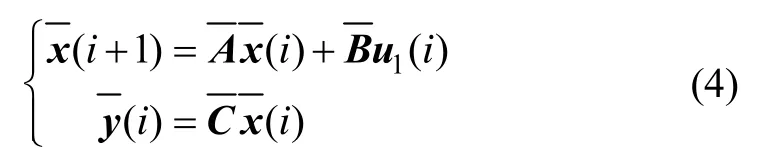
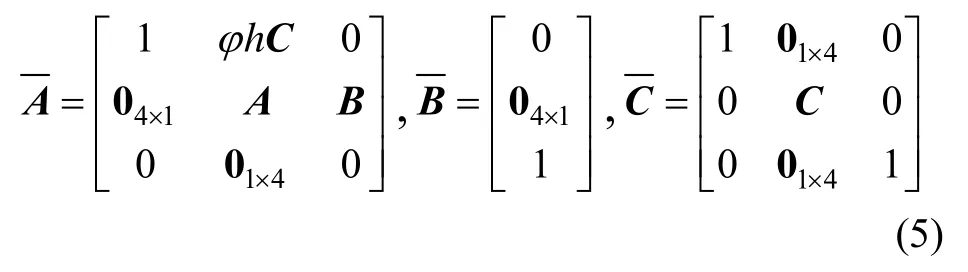
4）运用龙伯格最小维观测的原理，建立测量系统最低阶输出的动态控制器。

结合龙伯格降维观测器的原理，写出测量最低阶输出的动态控制器方程：

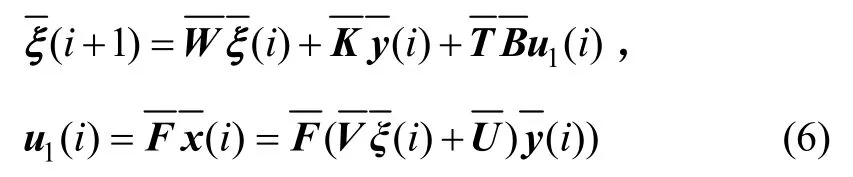
式中，正定对称矩阵P、S是Riccati方程的解：

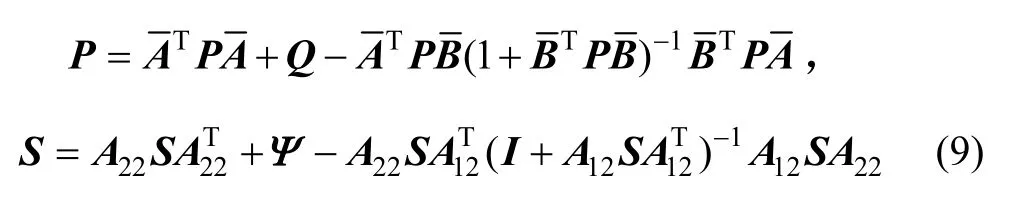
其中，正定阵Q、Ψ是某一加权矩阵。为了构建控制器模型，把分块得，控制器(6)表示成：

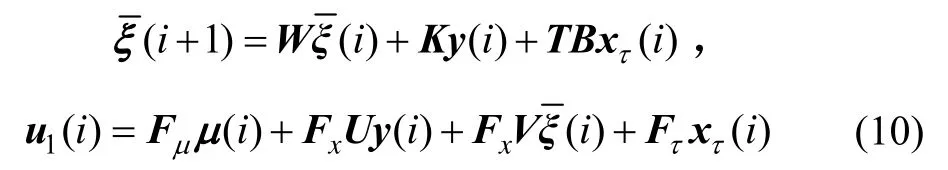
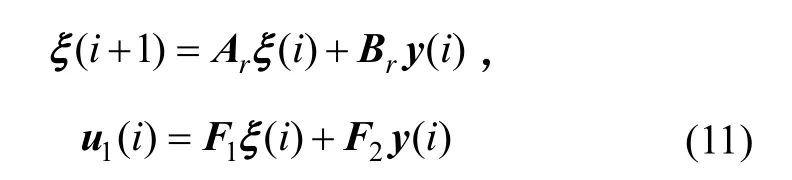
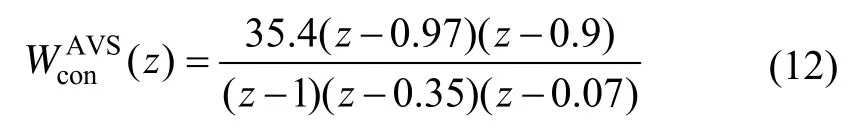
4 稳定回路控制器设计

稳定回路控制系统设计包括确定转换系数和设计稳定回路控制器两部分。

根据回路的无静差性确定稳定回路转换系数。测量回路中对应力矩关系有：

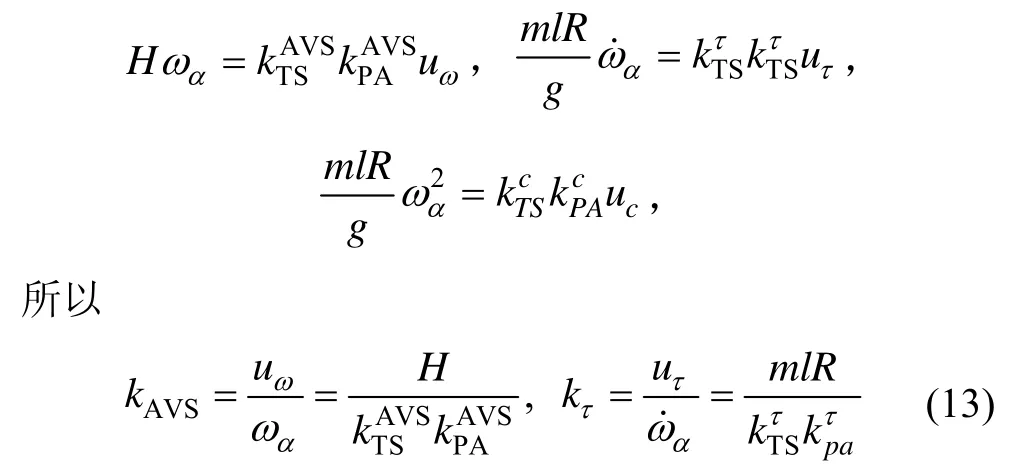
测量回路将测得角速度信息传入稳定回路，保证系统的稳定性，再考虑阻力矩最小化装置和测试平台，省略不必要的环节，得出稳定回路的结构框图如图 3所示。

稳定回路控制器使用离散PID控制器，满足无静差要求。先求出模拟形式的控制器。

断开图3主反馈，求得开环传递函数为：

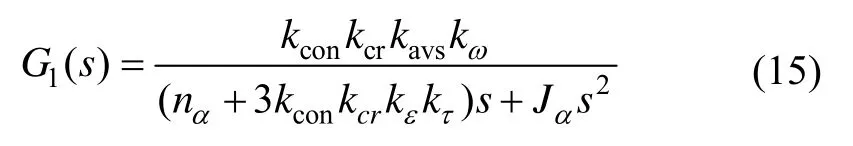
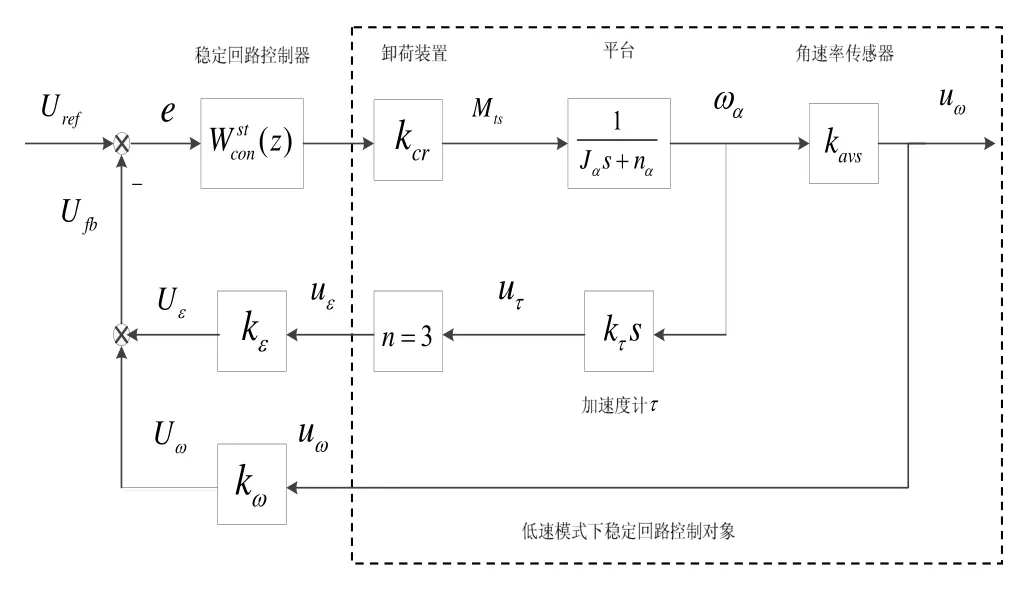
图3 低速模式稳定回路结构框图Fig.3 Structure of stabilization loop in the low rate mode

离散PID控制器为：

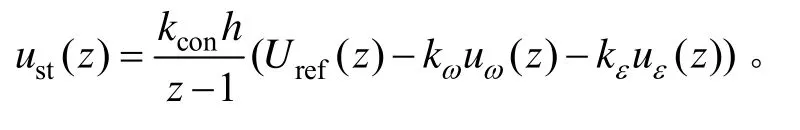
将已有转台功能元件参数代入到控制器方程中，得出稳定回路控制器为：

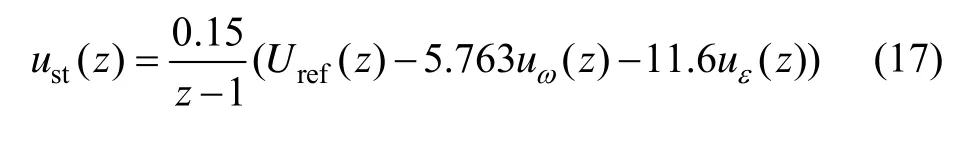
5 仿真结果分析

以角速度传感器测量回路为例，写出其开环传递函数，得出角速度传感器测量回路Bode图如图4所示。由图4得出，角速度传感器测量回路的相角裕度约为 45°，可以认为引入测量回路控制器后，角速度传感器测量回路具有高鲁棒性。对加速度计测量回路进行分析，也可以得到相同结论，由此构成的数字控制系统可具有高鲁棒性。

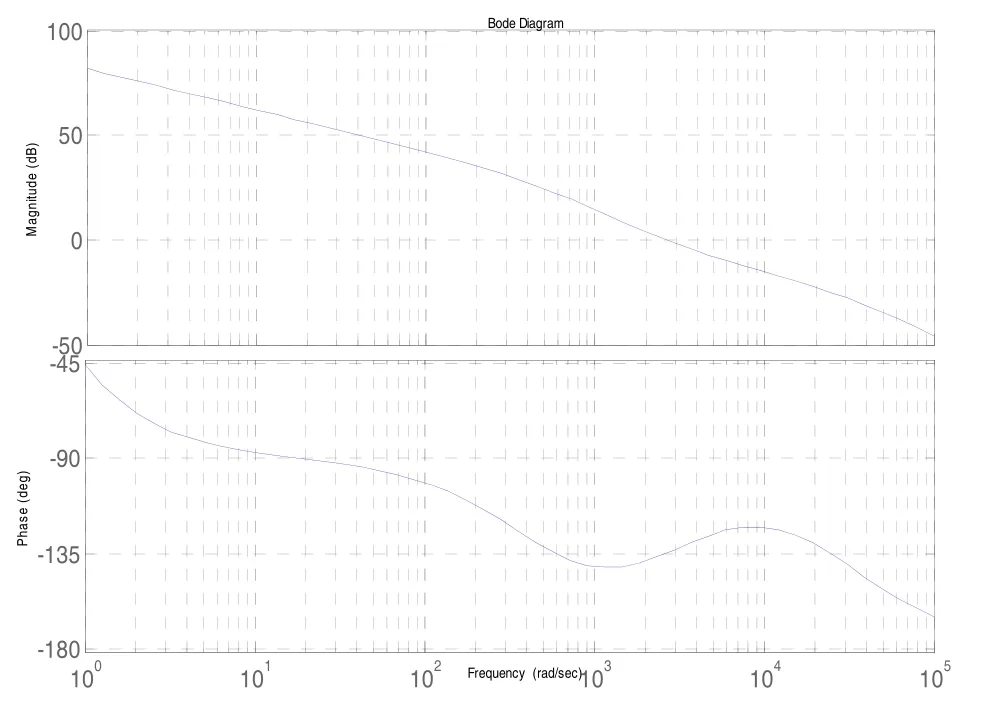
图4 角速度传感器测量回路Bode图Fig.4 Bode diagram of the angular velocity sensor measurement loop

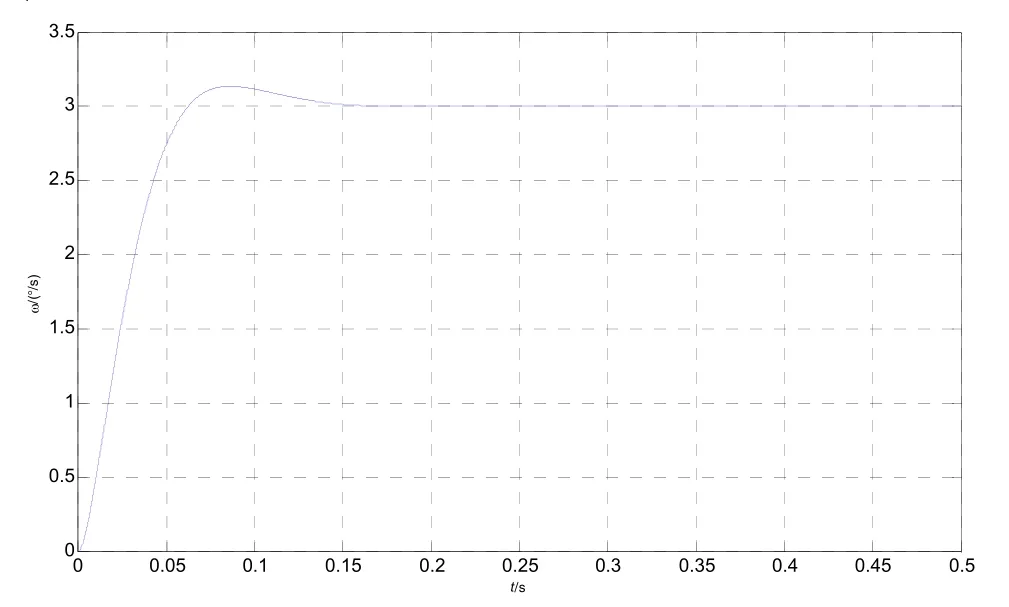
图5 转台主轴转速的阶跃响应Fig.5 Step response of the turntable’s main axis angular rate

传统转台的完整控制系统结构示于图 6，系统包括电流环、速度环和位置环，根据系统建模可得速度环的闭环传递函数为：

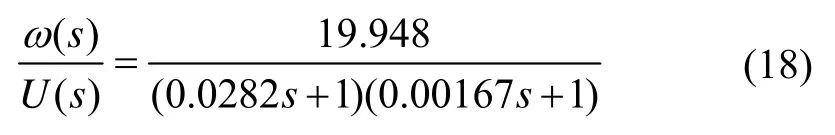
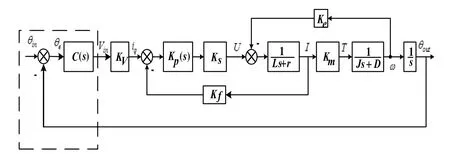
图6 传统转台控制系统结构框图Fig.6 Block diagram of conventional turntable’s control system

对速度环的阶跃响应进行仿真，结果示于图 7。可以看出，仅考虑速度环调节效果时，传统转台速度环输出ω超调量约为13%，有10%的稳态误差，响应时间约为9 s。

图7 传统转台速度环阶跃响应Fig.7 Step response of conventional turntable’s velocity loop

6 结 论

根据对转台系统的测量回路和稳定回路控制器的设计过程和Matlab软件仿真结果，可以得出如下结论：

1）引入惯性敏感元件测量转台的瞬时角速率，并对其进行反馈和控制，可以提高转台的速率精度和速率平稳性。

2）由于引入了稳定回路，保证了转台闭环系统以及每个子回路具有良好的鲁棒性。

3）根据转台主轴转速的阶跃响应，得出由于将惯性器件引入到转台测试系统中，不必通过主轴的大转动惯量保证速率平稳性指标，因此转台的重量大幅减小。

仿真结果表明，响应时间可减小到0.15 s，可以实现转速的快速调节和稳定，有利于陀螺仪表的动态测试，并且能显著缩短测试和标定时间。本文研究的新型转台顺应了惯性器件测试设备小型化和高精度化的趋势，可以为今后新型转台的研制提供一定的借鉴。

（References）：

[1]金涛，刘樾.对发展我国惯性测试技术的几点思考[J].航空精密制造技术，2006，42(5)：8-9.JIN Tao,LIU Yue.Thoughts on the development of the domestic inertial test technology[J].Aviation Precision Manufacturing Technology,2006,42(5):8-9.

[2]李拥军，杨文淑，范永坤，等.高精度转台摩擦力矩补偿控制器设计与仿真[J].光电工程， 2008，35(12)：126-130.LI Yong-jun,YANG Wen-shu,FAN Yong-kun,et al.Controller design and simulation for friction moment compensation on high-precision turntable[J].Opto-Electronic Engineering,2008,35(12):126-130.

[3]徐国柱，刘樾，孟凡军.利用加速度反馈改善转台低速性能[J].中国惯性技术学报，2008，16(4)：502-504.XU Guo-zhu,LIU Yue,MENG Fan-jun.Improving low-rate performance of turntable by acceleration feedback [J].Journal of Chinese Inertial Technology,2008,16(4):502-504.

[4]Haidekker M A.Linear feedback controls[M].London,UK:Elsevier,2013:193-208.

[5]Papadopoulosa K G,Tselepisb N D,Margaris N I.Type-III closed loop control systems-Digital PID controller design[J].Journal of Process Control,2013,23(10):1401-1414.

[6]Yang Yafei,Zhang Xiang,Li Jianguo.Mechanism analysis of instantaneous angular-rate measurement of gyro-test turntable with inertial devices[C]//Proceeding of the 8th International Symposium on Precision Engineering Measurements and Instrumentation.2012.

[7]杨亚非，张翔.带有惯性敏感器件的新型陀螺测试转台系统建模[J].中国惯性技术学报， 2013，21(6)：111-116 YANG Ya-fei,ZHANG Xiang.System modeling for new type of gyro-test turntable with inertial sensors[J].Journal of Chinese Inertial Technology,2013,21(6):111- 116.

[8]Кaпиxмaн Д M.陀螺仪表动态测试用精密控制转台[M].杨亚非，张明华，译.哈尔滨：哈尔滨工业大学出版社，2013：21-60.

[9]Deputatuva E A,Kalikhman D M,Polushkin A V,et al.Digital stabilization of motion of precision controlled base platforms with inertial sensitive elements.I.Application of float angular velocity sensor[J].Journal of Computer and Systems Sciences International,2011,50(1):117-129.

[10]Deputatuva E A,Kalikhman D M,Polushkin A V,et al.Digital stabilization of motion of precision controlled base platforms with inertial sensitive elements.II.Application of float angular velocity sensor and pendulum accelerometer[J].Journal of Computer and Systems Sciences International,2011,50(2):309-324.

Controller design for a new type of gyro-test turntable with inertial sensors

YANG Ya-fei,ZHANG Xiang
(Control and Simulation Center,Harbin Institute of Technology,Harbin 150080,China)

Angle measuring devices are used to measure the angular velocity of gyro test turntables with traditional principle whose precision has great relation with the chosen angle (or timeinterval).Though various control methods are applied to increase the turntable’s rate accuracy and rate stability,yet the test and control precision obtained is not quite satisfactory.A new principle of measuring the velocity is proposed which introduces inertial sensitive devices into the system and increases the rate accuracy and rate stability through the feedback and control of instantaneous velocity to truly reflect rate accuracy and rate stability of the turntable.The control system composition with inertial sensitive devices is discussed.When conducting the design for the system,the closed loop is divided into the measurement loop and stabilization loop,and digital control is applied to solve the problem of controller synthesis.Matlab is used to analyze the response process of the main variable in the system.Lastly,along with the controller design and analysis of the obtained model,it is verified that in comparison with the traditional turntable,the new turntable system has better robustness,the response time is 0.15 s,and the turntable is more suitable for gyro’s dynamic test.

gyroscopes;instantaneous angular rate;rate accuracy;rate stability;controller synthesis

TP273

：A

1005-6734(2014)01-0135-06

10.13695/j.cnki.12-1222/o3.2014.01.027

2013-09-22；

：2014-01-02

杨亚非(1968—)，男，博士，副教授，研究方向为导航、制导与控制。E-mail：yafei@hit.edu.cn