基于FPGA内部自激振荡与温度相关性的温度传感器

宋凝芳，赵亚飞，金 靖，潘 雄，黄云龙，张忠刚

（北京航空航天大学 仪器科学与光电工程学院，北京 100191）

基于FPGA内部自激振荡与温度相关性的温度传感器

宋凝芳，赵亚飞，金 靖，潘 雄，黄云龙，张忠刚

（北京航空航天大学 仪器科学与光电工程学院，北京 100191）

温度是IMU及其他导航器件等精密仪器中需要监测的重要参数，传统的温度监测一般使用热电偶或者数字温度传感器（如DS18B20）等，监测程序复杂，功耗高，因此使用精密仪器中广泛采用的FPGA芯片独立完成高集成度、低功耗温度监测具有重要意义。在FPGA中通过搭建环形振荡器产生了自激振荡信号，该信号周期与FPGA芯片温度具有正相关性，通过对振荡信号周期的检测完成了对温度的监测，设计了一种以 FPGA芯片同时作为敏感头和处理模块的温度传感器。通过对 Xilinx Virtex-2系列FPGA芯片进行实验，得到该传感器在-40℃～+60℃的范围内具有优于0.1℃的分辨率，优于 0.5℃的检测精度，满足一般温度监测需要。实验表明该传感器具有功耗低、集成度高、可靠性好等优点。

IMU；FPGA；自激振荡；温度传感器

温度对于 IMU及其他导航器件来说是需要检测的重要参数，直接影响着导航器件的补偿效果与系统的正常工作。由于FPGA广泛应用于IMU及其他导航器件中，用于完成导航等功能的控制，因此传统应用中一般使用FPGA控制外部独立的温度传感器（例如DS18B20）完成温度的采集，这样增加了系统原有控制软件代码的复杂度，同时使得系统的功耗较高。因此在 FPGA 中进行温度检测功能集成有着现实需求以及实现条件。

目前国内外对于FPGA实现温度检测已经有了一些研究[1-5]，原理主要有温度—电流、温度—周期、TFO（热反馈振荡器）等，均通过将温度数据转化为电信号来实现温度检测。

本文利用FPGA内部自激振荡信号的周期与温度的相关性，设计了一种以FPGA芯片自身同时作为敏感头和处理模块的温度传感器，属于温度—周期类温度传感器。此传感器只需对 FPGA进行顶层设计，而无需为电路部分添加其他额外器件及电路，即可实现对FPGA芯片及周围环境温度的实时监测。相较于传统温度传感器，该传感器功耗低、集成度高、可靠性好。

1 FPGA作为敏感头的温度传感器性能分析

1.1 FPGA作为敏感头的温度传感器原理

信号在数字电路中传输过程中，发生电平转换时会有一定的上升时间或下降时间，随着温度的上升，半导体器件中的载流子浓度降低，器件的转换速度变慢，上升时间和下降时间变长，信号的延时增大，反之则相反[6-8]。因此如果器件中存在一个由内部电路自激振荡形成的周期信号，其周期由于延时随温度变化会产生相应的改变，通过检测此周期信号的周期即可获取相应的温度。以上即为 FPGA作为敏感头的温度传感器的基本原理，原理图如图1所示。

图1中，Clock_s为自激振荡器产生的时钟信号，相当于传统传感器中的敏感头，此信号波形特点与稳定性直接关系到整个系统的精度，具有较小上升沿和下降沿并且频率较低的 Clock_s更有利于信号的检测及系统性能的提高；Clock_m为Clock_s经过温度调制后产生的信号，其周期相对于Tclock_s已经发生了改变；周期信号检测部分直接影响了系统的输出数字量及检测精度，采用简单易行且精度较高的方法实现周期的检测可以有效的降低系统的复杂程度，提高系统性能；最后将代表温度的数字量随角速度数据传输至PC机进行显示、存储和分析。

图1 FPGA作为敏感头的温度传感器原理框图Fig.1 Architecture of temperature sensor using FPGA as sensing part

1.2 FPGA作为敏感头的温度传感器性能分析

对于IMU和其他导航器件的温度检测来说，此温度传感器的适用范围一般满足-40℃～+60℃即可，IMU自身使用的工业级FPGA芯片工作的温度范围一般为-40℃～+100℃[9]，可以满足要求；由于温度监测一般不需太高的精度，因此本系统具备0.5℃的分辨率和1℃的检测精度就可以满足要求；对于数据更新率，采用不低于1 Hz的输出即可完成温度的跟踪。

2 FPGA作敏感头的温度传感器系统设计

本部分内容根据FPGA作为敏感头的温度传感器原理以及其需要达到的性能选择 Xilinx公司的XC2V1000芯片为目标芯片搭建系统。系统构成方面，温度传感器主要包括自激振荡器和信号检测及采集部分。具体实现方面，在自激振荡器设计中，通过采用效果显著的延时环节既减少了资源占用，降低了功耗，又提高了自激振荡信号的波形稳定性；在信号检测及采集部分设计中，通过把对目标信号进行高倍数分频及使用高频时钟计数法检测周期二者相结合，有效地提高了目标信号的稳定性及可检测性，从而最终提高了系统的分辨率及精度。

2.1 自激振荡器的设计

自激振荡信号产生的基本原理如图2所示。

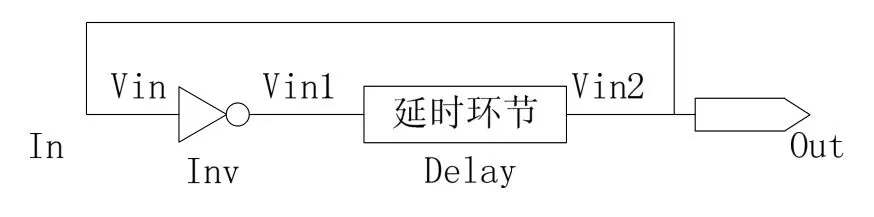
图2 自激振荡器的基本原理框图Fig.2 Architecture of self-oscillator

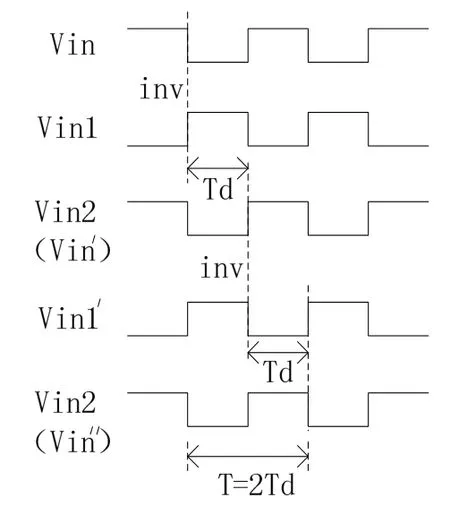
图3 自激振荡信号产生时序图Fig.3 Signal sequence diagram of self-oscillation

图2中直线表示电气连接，Inv为反相环节，这里将其作为理想的反相环节，即无延时、仅有电平翻转、无上升时间和下降时间；Delay为延时为Td的理想延时环节。自激振荡器产生振荡信号的时序如图3所示。

图3中Vin为初始输入信号，假定某个时刻Vin由于外界的扰动发生了由高到低的跳变，则此信号经过反相环节变为信号Vin1，之后经过延时环节发生了Td的延时得到Vin2（Vin′），这时已经出现了周期信号的低电平半周期，Vin2（Vin′）信号同时又作为下一个输入信号，经过反相产生信号Vin1′，此信号再通过延时环节发生Td的延时得到新的Vin2（Vin″），这样周期信号的高电平半周期就产生了，如此往复即在Vin2处产生了周期为T=2×Td的周期信号[10]。

常用的自激振荡器一般采用奇数个非门直接做环形级联形成[11]，非门同时作为反相和延时环节，此类自激振荡器在实现起来有三个缺点，一是随着大规模集成电路技术的快速发展，非门的延时效果越来越小，从而可能需要大量的非门才能完成一定的延时，这就增大了功耗；二是非门的延时效果不稳定，从而可能导致自激振荡时钟周期常温下的不稳定，直接影响测试结果；三是不加约束情况下，FPGA设计软件（如ISE Foundation）会在综合过程中将多余的非门当做冗余逻辑去掉，从而将奇数个非门级联优化为一个非门，达不到延时的效果，这样就可能无法在FPGA中形成振荡器。

另外一种在FPGA内部制作自激振荡器的方法是在ALTERA公司的FPGA中通过插入专门的LCELL等专用延时单元来完成延时，这种延时效果也比较好，并且 LCELL的延时大小也是随温度变化的，但是在这种FPGA中实现的自激振荡器移植性很差，尤其在不同公司的FPGA之间。

基于以上考虑，本传感器在搭建过程中采用单非门来实现电平的翻转和微延时，采用缓冲门来实现主要延时，这样既能通过占用较少的资源完成频率稳定且较低的自激振荡信号的产生，又可以保证程序有很好的移植性。本传感器FPGA内部自激振荡器实现的电路原理图如图4所示。

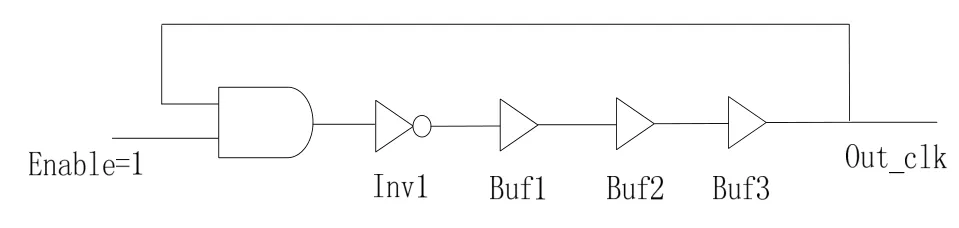
图4 FPGA内部自激振荡器原理图Fig.4 Architecture of self-oscillator in FPGA

图4中与门主要完成自激振荡器的使能控制，使用时可根据需要进行选通控制，当Enable=1时环形振荡器起振，Out_clk输出时钟信号，Enable=0时振荡器不振荡；非门主要完成电平的翻转，这二者延时作用不明显，可以忽略，后边的Buf采用了FPGA中的BUFGMUX，其具有显著的延时功能，是主要的延时环节。

2.2 信号检测及采集部分设计

本部分要实现的重要功能是实时测量自激振荡信号的周期，测量一个振荡信号的周期一般有两种办法：

一是在给定时间(t1)内对自激振荡周期(T1)进行计数(N1)，则测得的周期为T1=t1/N1，此种方法的最大测量误差为自激振荡周期T1，而T1是一个随着温度变化的量，因此误差是不可控的。

二是在自激振荡信号的半周期(T1/2)内对高频时钟周期(T0)进行计数(N2)，则测得的周期为T1=T0·N2/2，此种方法的最大测量误差为T0。由于过多增大高频信号的频率会超出FPGA的承受能力，因此此类方法可能导致N2较小，从而使得相对误差会较大。

综合以上两种方法，本传感器信号检测部分进行了相应改进，即对自激振荡信号先分频增大周期，再使用高频信号进行填充计数，可以理解为第二种方法的变形。首先对自激振荡信号(T1)进行高倍数(n)分频，减小高频信号上升沿和下降沿带来的检测误差的同时还可以提高分辨率；然后使用高频时钟(T3)对分频后的时钟信号进行填充计数(N)来检测目标信号周期，此种检测方法既通过第一步放大了待测自激振荡信号的周期，又通过第二步有效控制了系统测试的最大误差，从而可以在保证系统压力较小的前提下有效地提高系统检测精度，且可以通过调节分频系数调整系统的分辨率。信号检测部分原理如图5所示，输出数字量见公式(1)。

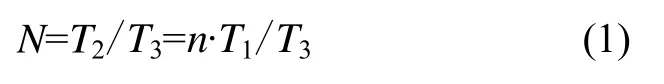
数字量N即为本温度传感器的输出，设定N值为16位数字量，按照1 Hz的数据更新率随角速度数据传输至上位机中进行显示、存储和分析。

图5 信号检测原理图Fig.5 Architecture of signal detecting

3 实验结果及讨论

3.1 环形振荡器实验结果

根据2.1中设计完成的环形振荡器输出振荡信号的周期和Buf的个数成正比，且具有很好的稳定性。其常温下相关性如图6所示。

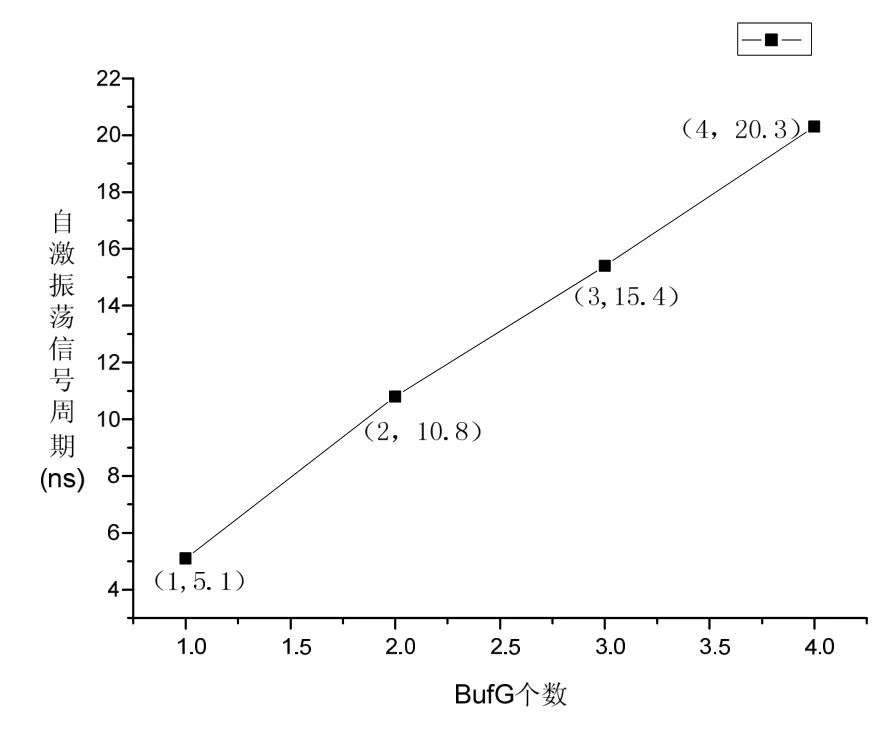
图6 环形振荡器输出信号周期与BUF个数相关性Fig.6 Relativity of numbers between BUF and signal period from self-oscillator

考虑到FPGA正常工作的频率范围以及FPGA资源利用率，本传感器采用了三缓冲方案，自激振荡信号的周期为15.4 ns。设定分频系数为20000，填充用高频时钟信号频率为 50 MHz，可知系统的检测绝对误差为20 ns，相对误差为20/(15.4×20000) =0.0065%，利用式(1)可得常温下本温度传感器输出量在 7700左右（仅对正半周期进行填充计数）。

3.2 FPGA作为敏感头的温度传感器实验结果

实验设计为恒温实验和变温实验，均在恒温箱设定的环境中进行实验，其中恒温箱已经经过标准温度传感器标定。由于目前IMU中常用DS18B20等器件作为温度检测器件，因此在实验过程中采用DS18B20数字温度传感器进行对比实验，其输出采用16位，分辨率为 0.0625，测量温度范围为-55℃～+125℃，在-10℃～+85℃范围内，精度为±0.5℃。

3.2.1 恒温实验

恒温实验采用恒温箱设置外界温度，实验中设置了6个恒温温度点，分别是-40℃、-20℃、0℃、20℃、40℃和60℃，主要用于研究FPGA温度传感器输出与温度的线性关系。

恒温实验数据处理后结果如表1所示，其中均值1和标准差1均为DS18B20输出，均值2和标准差2均为FPGA温度传感器输出。

表1 恒温实验数据处理结果Tab.1 Results of invariable-temperature test

以表1中温箱的温度设定值为自变量x，以FPGA温度传感器输出均值和 DS18B20输出均值分别作为因变量y1、y2作图，结果如图7所示。

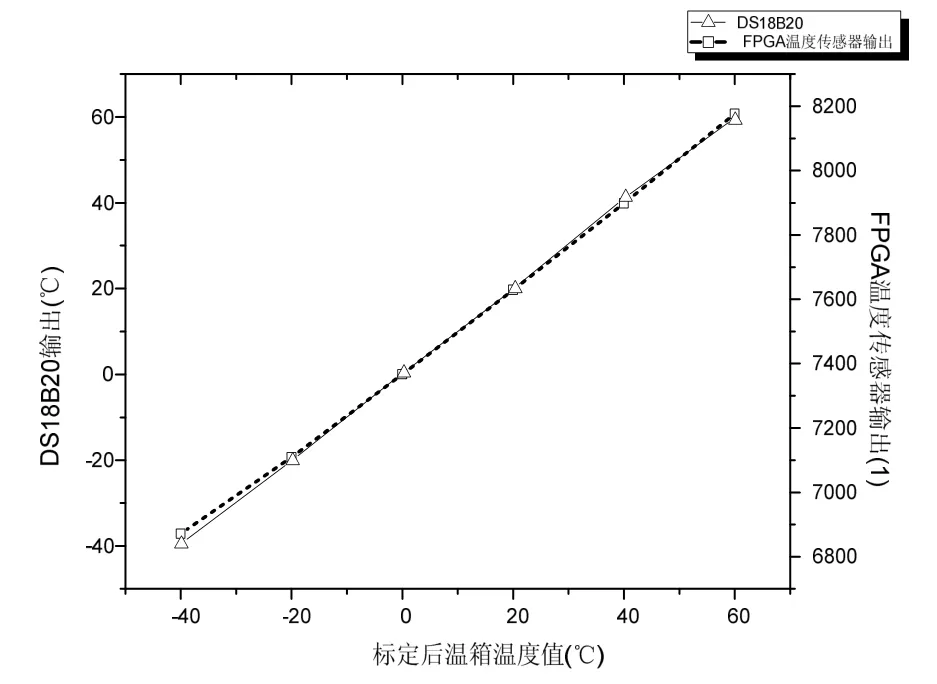
图7 DS18B20与 FPGA温度传感器恒温测试输出Fig.7 Invariable-temperature test output of DS18B20 and FPGA temperature sensor

通过恒温实验发现由FPGA实现的温度传感器的输出均值在不同的恒定温度上有着很好的梯度分布，和DS18B20的测试结果趋势相似，只是通过表1可以发现在同一温度下FPGA温度传感器的输出有明显噪声（输出数据的方差）存在，但是相对于输出数字量在0.02%左右，在可接受范围内。

为了将FPGA温度传感器的输出转化为相应的温度值，需要明确二者之间的转换关系，即函数关系。

以表1中恒温箱设定温度为y值，以FPGA温度传感器输出均值为x值，采用最小二乘法对数据进行线性拟合，所得直线如图8所示。

最小二乘拟合所得函数式如公式(2)所示：

由式(2)可知其分辨率(k值)可以达到0.07645℃，根据上式将各恒温段FPGA输出转化为温度值，其标准差均介于0.2～0.5之间。

观察图7发现图中FPGA温度传感器输出曲线有折线部分，因此又采用了分段线性拟合处理数据。拟合系数如表2所示。

图8 设定温度与 FPGA温度传感器输出最小二乘拟合直线Fig.8 Least squares estimate result of temperature set and output of FPGA temperature sensor

由表2可知此种拟合方法分辨率(k值)最差也可达0.0786℃，根据上表将各恒温段FPGA输出转化为温度值，其标准差介于0.2～0.4之间。

表2 设定温度与FPGA温度传感器输出分段拟合系数Tab.2 Piecewise linear fitting coefficients of temperature set and output of FPGA temperature sensor

由上述两种不同处理方法的结果可知，FPGA温度传感器的输出与温度之间存在一个接近线性的关系，直接使用纯线性关系来换算，其分辨率等也在可接受范围内，如果使用分段线性拟合，则可以更加准确的将输出数字量转化成温度值。

3.2.2 变温实验

变温实验中采用“常温-60℃～-40℃—常温”温度变化过程测试，温度变化率为 1℃/min，主要用于研究传感器的温度适用性以及线性关系优化。

恒温箱温度变化曲线如图9所示。按照图9所示温度变化使用DS18B20和FPGA温度传感器同时测试，测试结果如图10所示。

为了验证 FPGA温度传感器在变温情况下的性能，分别采用最小二乘线性拟合方法和分段线性拟合方法将FPGA温度传感器输出换算成温度值，结果分别如图11、图12所示。

图9 恒温箱温度设定曲线Fig.9 Test curve of temperature set by incubator

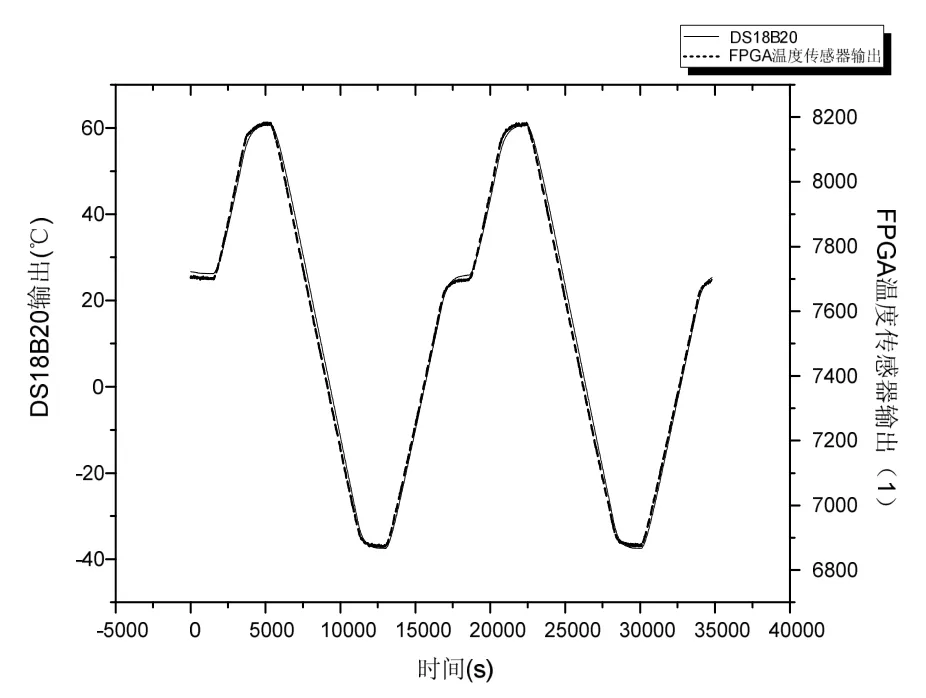
图10 DS18B20与FPGA温度传感器变温测试结果Fig.10 Test result of FPGA temperature sensor and DS18B20 at variable temperature

图11 最小二乘拟合法FPGA温度传感器输出Fig.11 Output of FPGA temperature sensor using the least squares estimate method

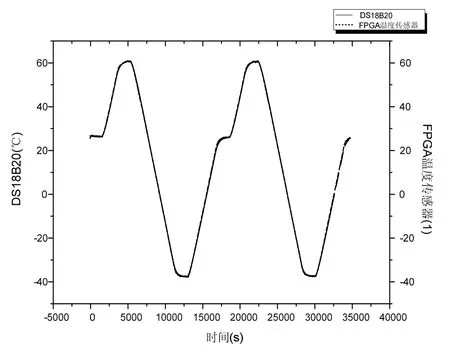
图12 分段线性拟合法FPGA温度传感器输出Fig.12 Output of FPGA temperature sensor using the method of piecewise linear fitting

采用最小二乘线性拟合方法计算得出FPGA温度传感器相对于 DS18B20温度芯片的测试温度最大相对误差为(4.2/100)×100%=4.2%。

采用分段线性拟合方法计算得出FPGA温度传感器相对于 DS18B20温度芯片的测试温度最大相对误差为(1.5/100)×100%=1.5%，误差显著降低，与恒温实验结果相符合。

通过变温实验可以发现本传感器在-40℃～+60℃的范围内能够很好的跟踪温度的变化，具有良好的线性度和全温适用性。但是FPGA温度传感器输出有一定的延迟（曲线变化未完全重合），分析主要是由于外界的温度对FPGA的影响需要透过FPGA封装，因此产生了温度检测的延迟，但是延迟较小，对于IMU或其他导航器件的温度需求基本没有影响。

4 结 语

本文设计了一种基于FPGA内部自激振荡周期与温度相关性的新型温度传感器。此温度传感器以FPGA为敏感头和处理模块，通过软件设计集成到FPGA中，通过在恒温箱中进行恒温和变温实验发现，本系统在-40℃～+60℃检测范围内可以保证优于0.1℃的分辨率，优于0.5℃的检测精度，表现出良好的恒温和变温实验性能。但是由于此温度传感器目前只在单一型号FPGA上实现，因此在通用性和移植性上需要进一步研究和验证。

（References）：

[1]Chen P,Shie M -C,Zheng Z -Y,Zheng Z -F,Chu C -Y.A fully digital time-domain smart temperature sensor realized with 140 FPGA logic elements[J].IEEE Trans.Circuits and Systems I,2007,54(12):2661-2668.

[2]Woo K,Meninger S,Xanthopoulos T,Crain E,Ha D,Ham D.Dual-DLL-based CMOS all-digital temperature sensor for microprocessor thermal monitoring[C]//Proc.IEEE ISSCC Dig,2009:68-69.

[3]Chen Poki,Chen Shou-Chih,Shen You-Sheng,Peng You-Jyun.All-digital time-domain smart temperature sensor with an Inter-Batch inaccuracy of 0.7℃-0.6℃after one-point calibration[J].IEEE Trans.Circuits and Systems I:Regular Papers,2011,58(5):913-920.

[4]Souri K,Chae Y,Makinwa K A A.A CMOS temperature sensor with a Voltage-Calibrated inaccuracy of ± 0.15 ℃(3σ) from 55℃ to 125℃[J].IEEE Journal of Solid- State Circuits,2013,48(1):1-10.

[5]Pertijs M A P,Makinwa K A A,Huijsing J H.A CMOS smart temperature sensor with a 3σ inaccuracy of ±0.1 C from -55℃ to 125℃[J].IEEE Journal of Solid-State Circuits,2005,40(12):2805-2815.

[6]Kim C K,Lee J G,Jun Y H,Lee C G,Kong B S.CMOS temperature sensor with ring oscillator for mobile DRAM self-refresh control[J].Microelectronics Journal,2007,38:1042-1049.

[7]Lin Y S,Sylvester D,Blaauw D.An ultra low power 1V,220nW temperature sensor for passive wireless applications [C]//Proc.CICC.2008:507-510.

[8]Chen P,Chen C C,Tsai C C,Lu W F.A time-todigital-converter-based CMOS smart temperature sensor [J].IEEE Journal of Solid-State Circuits,2005,40(8):1642-1648.

[9]Chen P,Wang K M,Peng Y H,Wang Y S,Chen C C.A time-domain SAR smart temperature sensor with -0.25℃～+0.35℃inaccuracy for on-chip monitoring[C]//Proc.Eur.Solid-State Circuits Conf.,2008:70-73.

[10]Chung Ching-Che,Yang Cheng-Ruei.An all-digital smart temperature sensor with Auto-Calibration in 65nm CMOS technology[C]//Proceedings of 2010 IEEE International Symposium on Circuits and Systems.2010:4089-4092.

Temperature sensor based on relativity between self-oscillation in FPGA and temperature

SONG Ning-fang,ZHAO Ya-fei,JIN Jing,PAN Xiong,HUANG Yun-long,ZHANG Zhong-gang
(School of Instrument Science and Opto-electronics Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Temperature is an important parameter that needs to be monitored in IMU and other navigation devices.Thermocouple or digital temperature sensor(such as DS18B20) is usually used in temperature detecting,so a highly integrated and low-cost temperature detecting design in FPGA is important.In this paper,the self-oscillation signal was generated by ring oscillator set up in FPGA and its period had positive relativity with the FPGA’s temperature,so the temperature could be gotten by detecting the period of self-oscillation signal.In the end,a temperature sensor using FPGA as both sensing part and processing part was designed.Experiments on the FPGA chip of series Virtex-2 from Xilinx show that the resolution is better than 0.1℃ and the accuracy is better than 0.5℃ within -40℃～+60℃,which can satisfy the general requirement in monitoring temperature.The temperature sensor is low-cost,highly integrated and highly reliable.

IMU;FPGA;self-oscillation;temperature sensor

TH811

：A

1005-6734(2014)01-0026-06

10.13695/j.cnki.12-1222/o3.2014.01.007

2013-08-27；

：2013-12-02

航空科学基金资助项目（2011ZC51032）

宋凝芳（1968—），女，研究员，博士生导师，从事光纤陀螺、组合导航研究。E-mail：songnf@263.net