极区飞行间接格网惯性导航算法

周 琪，岳亚洲，张晓冬，田 宇

（1.飞行器控制一体化技术国防重点实验室，西安 710065；2.中航工业西安飞行自动控制研究所，西安 710065）

极区飞行间接格网惯性导航算法

周 琪1,2，岳亚洲1,2，张晓冬1,2，田 宇1,2

（1.飞行器控制一体化技术国防重点实验室，西安 710065；2.中航工业西安飞行自动控制研究所，西安 710065）

为克服极区经线收敛引起的惯导系统定位定向难题，同时为实现中低纬度地区和高纬度地区导航算法形式的统一，提出了以游移方位惯导编排为内核的极区间接格网导航算法。推导了游移坐标系和格网坐标系间的方向余弦矩阵，以此可间接获取格网航向和格网速度，同时用地心地固坐标替换经纬高定位参数，解决了极区的导航定位问题。仿真分析了两组特定飞行轨迹下的算法性能，并与直接格网惯导力学编排算法进行了比较，结果表明二者导航精度相当，可满足极区导航的需要。

极区导航；间接格网导航；游移方位；方向余弦矩阵

具备极区导航能力是现代飞机跨极区飞行的基本条件，由于极区特殊的地理环境限制，诸如卫星导航、无线电导航、地磁导航等导航手段在极区无法正常工作[1-4]。惯性导航因其自主性、隐蔽性和信息的完备性使其成为极区导航的首选，但在极区由于经线收敛导致常规的基于地理真北方向参考线的指北方位惯导算法失效[5]。虽然游移和自由方位惯导可在极区完成姿态方向余弦矩阵和位置方向余弦矩阵解算，但从位置方向余弦矩阵中提取游移角和经度信息时存在奇异值[6]。有效地解决手段是对极区的定位和定向采用另一组合理的表征参数，其中格网航向是有效手段之一[6]，美F-16战机导航手册上亦指出极区导航应采用格网航向作为参考，同时一些对应的极区航图也得到了快速发展[7]。

文献[8-9]在定义格网坐标系的基础上推导了格网导航坐标系框架下以格林尼治子午线作为航向参考，地心地固（ECEF）坐标为定位参数的格网导航力学编排方程，有效解决了极区的定位定向问题。从文献[8]分析可以看出抑制经线收敛引起导航解算误差的手段是选择了新的航向参考线，同时用ECEF定位参数替换了经纬高定位参数。极区格网惯导力学编排是一套自身完备的极区导航方案，但若考虑全球执行能力时，正如文献[10]的分析，格网导航编排在赤道附近无法正常工作，需要采用指北+格网编排或游移+格网编排的形式。这样，一方面需要引入新的力学编排方案，破坏了传统编排方案的完整性、连续性和唯一性；而在逻辑设计方面需要考虑多种编排方案间的切换方式以及切换过程中各参数间的转换关系，增加了程序设计的复杂度和计算机计算的负担[10]。

鉴于格网惯导编排方案的上述优缺点，考虑到游移方位惯导力学编排具备全球范围内解算姿态方向余弦矩阵和位置方向余弦矩阵的能力，本文取长补短充分发挥二者的优点，以游移方位惯导力学编排作为全球执行解算的内核，在中低纬度地区将游移坐标系内的方位和速度通过游移坐标系和地理坐标系间的关系投影到地理坐标系内，得到地理真北航向和地理东、北、天向速度；在极区将游移坐标系内的速度和方位通过游移坐标系和格网坐标系间的关系投影到格网坐标系，得到格网北向和格网东、北、天向速度，并用ECEF定位参数替换经纬高定位参数。这样，中低纬度地区和高纬度地区的导航解算算法的内核统一，外在导航参数计算形式统一。概括而言，一个内在的力学编排参考坐标系，两个外在的导航参数表征参考坐标系可以解决惯导系统全球导航问题。

文章首先回顾了极区格网惯导力学编排的优缺点，为寻求中低纬度地区和高纬度地区导航形式的统一，推导了游移坐标系和格网坐标系间的转换关系；接着通过误差表达式阐述了格网参考坐标系下可以抑制误差随纬度升高而增长的内涵；最后仿真比较分析了格网力学编排方法和本文方法在极区导航的效果。

1 基于格网航向的极区导航

1.1 格网坐标系和游移坐标系的关系

如图1所示，飞机所在地P点处平行于格林尼治子午面的平面为格网平面，格网平面与当地水平面的交线为格网北向，地理真北方向同格网北向的夹角为σ，格网天向同地理天向重合，格网东向在水平面内且与格网北向垂直构成右手直角坐标系，此即为格网坐标系G，其各轴单位向量集记为。

图1中w表示游移坐标系，其相对当地地理坐标系g有α的偏角，其各轴单位向量集记为。

文中所用到的地理坐标系g、地球坐标系e和惯性坐标系i的定义可以参见文献[8]。

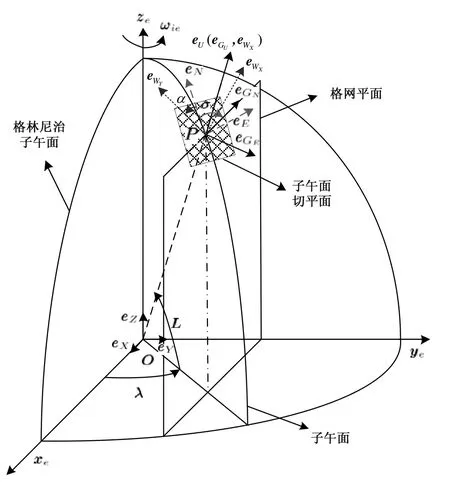
图1 格网系和游移系Fig.1 Grid frame and wander azimuth frame

设P点地理纬度、经度和高度分别为L、λ和h，由图1可知，格网坐标系和地理坐标系间的方向余弦矩阵为：

其中sinσ和cosσ定义如下[8]:

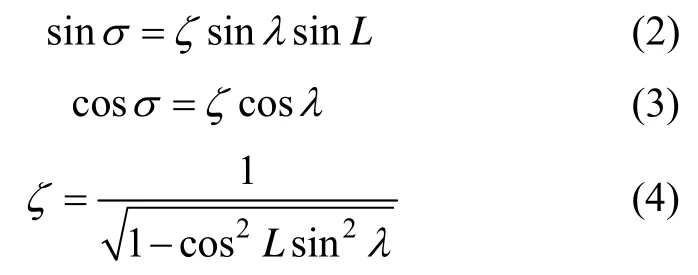
式中，c2L表示的缩写；cL表示cosL的缩写，其它缩写类同。

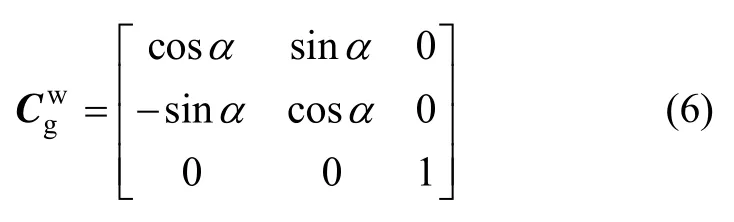
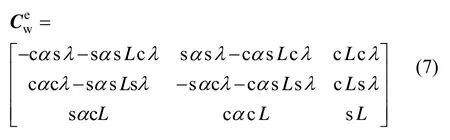
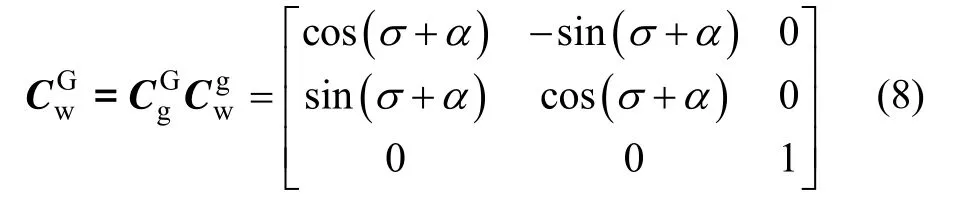
由式(5)和式(7)亦可得到格网坐标系和游移坐标系间的方向余弦矩阵为：

式(8)和式(9)表示的物理含义相同，但计算方式不同，式(8)需要分别计算出游移角α和格网北向与真北向夹角σ，而式(9)不需要此过程。

1.2 极区导航参数计算

游移方位惯导力学编排方程可以全球范围内计算游移导航坐标系下的姿态方向余弦矩阵和位置方向余弦矩阵，但在高纬度地区从位置方向余弦矩阵提取游移角和经度存在较大误差甚至会出现奇异现象，因此不应直接通过位置方向余弦矩阵求取定位参数，宜采用ECEF定位参数。由游移坐标系下的速度可以计算ECEF定位坐标：

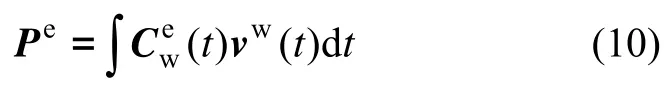
式(10)至(12)即为惯导在极区通过对游移导航编排参数在格网系的投影获得极区格网导航参数的计算公式，完整的计算流程如图2所示。

由图2可以看出整个导航过程分为三大部分：游移方位惯导力学编排方程、地理参考坐标系下的导航参数计算和格网参考坐标系下的导航参数计算，两种参考坐标系下的导航参数计算过程并行而互不影响。根据飞机所处纬度的高低选择对应的导航参数计算通道，也可以双通道并行运算，在中低纬度地区以地理参考坐标系下的导航参数作为飞机定位定向的参数；而在高纬度地区以格网参考坐标系下的导航参数作为飞机定位定向的参数。

图2 间接格网导航流程图Fig.2 Program architecture for indirect grid navigation

2 导航误差分析

由游移方位角α的定义可知：

对其求一阶全微分得：

由式(14)和式(15)知地理航向误差角与游移角误差有关，而包含tanL和secL项，当纬度L增大时增大且趋于无穷，故高纬度地区真北航向误差发散非常快而无法使用。

地理系下的速度为：

则东向和北向速度误差为：

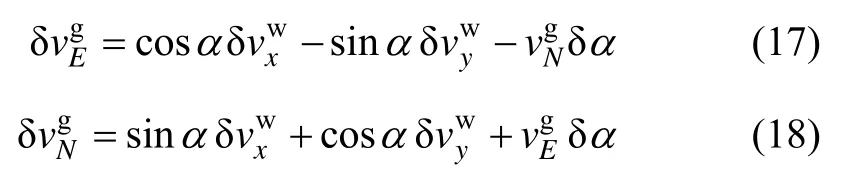
由式(17)和式(18)知，地理方向的水平速度误差与δα相关，从而导致高纬度地区地理水平速度发散非常快而无法正常使用。

由图1及式(8)可知格网坐标系下的格网方位误差角满足：

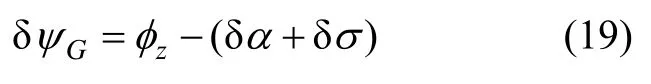
由式(12)可知格网水平东向和北向速度误差为：

对式(3)求一阶偏导数可得：

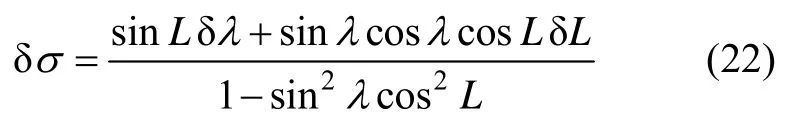
为简化分析，假设不存在纬度位置误差，则式(14)和式(22)分别简化为：

3 仿真分析

为验证文中方法的合理性，进行两组仿真试验。一组是沿高纬度某条纬线的圆周运动，另一组是跨极点运动。第一条轨迹的初始位置为[89.5°N,108°E,5000 m]，以300 m/s速度沿着89.5°N纬线飞行1 h；第二条轨迹的初始位置为[83°N,108°E,5000 m]，以300 m/s速度沿着108°E经线跨极点飞行2小时。仿真所用惯性器件性能参数为：陀螺随机常值漂移 0.01 (°)/h，随机游走系数；加速度计随机常值偏置40 μg，随机游走系数。仿真初始误差设置为：初始姿态误差[0.003,0.003,-0.06]°，初始速度误[0.01,0.01,0.01]m/s。

图3至图6所示为沿纬线飞行时不同参考坐标系下的航向误差、速度误差和位置误差比较图。

图3中第一幅子图为沿纬线飞行时真北航向误差，第二幅子图为游移航向误差、本文方法得到的格网航向误差以及格网力学编排得到的格网航向误差。从图中可以看出，地理真北航向误差振动迅速发散，而其他三种航向误差按时间趋势缓慢增长且基本重合，总体而言后者精度高于前者。

图4为四种坐标系下的水平速度误差，由于坐标系不统一，不能简单的通过单独比较而判断优劣。为此在图5中通过绘制四种水平速度误差的模值加以比较四种速度误差的优劣，由图可以看出，其他三种速度误差明显优于地理水平速度误差。但在相同的坐标系下，由图可以看出本文方法获得的格网水平速度误差和格网力学编排获得的速度误差精度相当。

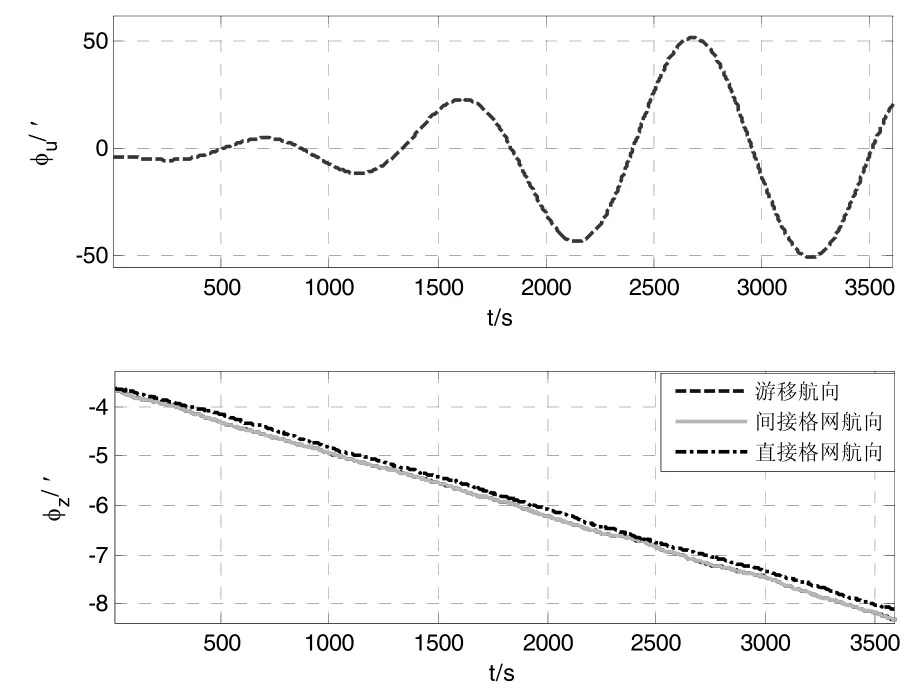
图3 沿纬线飞行时方位失准角Fig.3 Heading misalignment of latitude trajectory

图4 沿纬线飞行时水平速度误差Fig.4 Level velocity error of latitude trajectory

图5 沿纬线飞行时水平速度误差模值Fig.5 Norm of level velocity error of latitude trajectory

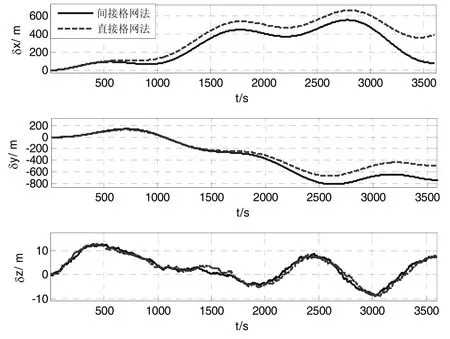
图6 沿纬线飞行时ECEF定位误差Fig.6 ECEF Position error of latitude trajectory

图6比较了本文方法和格网力学编排方法计算得到的ECEF定位误差，由图可以看出二者的定位精度相当。

图7至图10所示为沿经线飞行时不同参考坐标系下的航向误差、速度误差和位置误差比较图，各图的含义同图3至图6。在图7至图10跨极点飞行仿真误差图中可以明显看出地理真北航向误差和地理水平速度误差在接近极点处迅速增大直至溢出，而其他三种方法得到的航向、速度和位置精度相当。

图7 沿经线飞行时方位失准角Fig.7 Heading misalignment of longitude trajectory

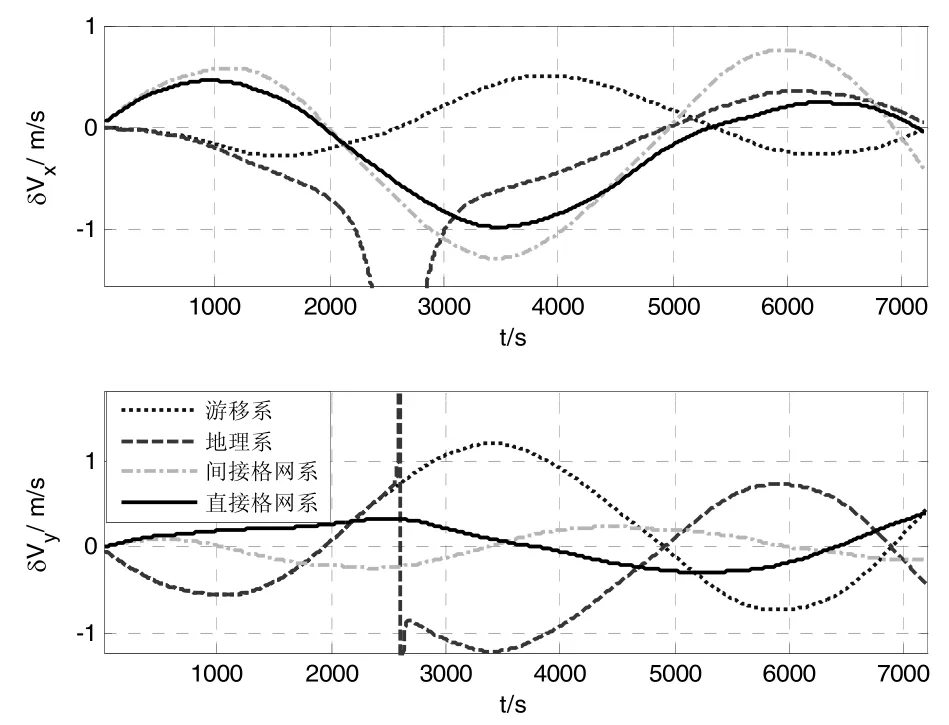
图8 沿经线飞行时水平速度误差Fig.8 Level velocity error of longitude trajectory

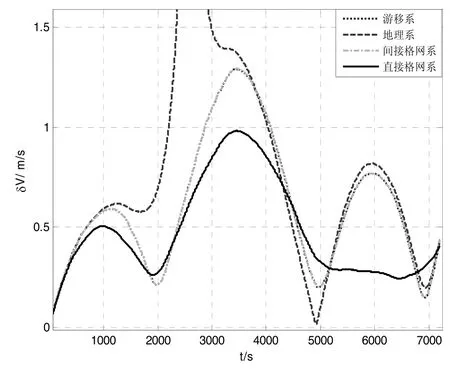
图9 沿经线飞行时水平速度误差模值Fig.9 Norm of level velocity error of longitude trajectory

图10 沿经线飞行时ECEF定位误差Fig.10 ECEF position error of longitude trajectory

由沿高纬线方向飞行和沿经线跨极点飞行仿真试验可以看出，地理航向和速度不能满足极区导航的需要，而格网航向、速度及ECEF定位参数可以满足极区导航的需要，且本文提出的基于格网航向的游移惯导极区导航算法和格网惯导力学编排算法具有相同的导航精度。

4 结 论

基于格网航向的游移方位惯导极区导航算法通过格网航向对游移惯导参数进行投影修正，在极区获得格网参考航向、格网参考速度和ECEF定位坐标。与通过真北航向对游移惯导参数进行投影获得地理参考航向、参考速度和经纬高定位坐标形成两路计算形式相似的并行导航参数输出通道，其中一个通道满足中低纬度地区导航，另一通道满足极区导航。

与格网力学编排算法相比，本文算法是解决极区导航症状的“外敷贴剂”，不伤筋动骨；而后者则是“功能器官再生疗法”，伤筋动骨但殊途同归疗效相当。间接格网导航参数和直接格网导航参数均可以方便的与极区航图配合使用，对于极地地区的扩展导航参数的计算也可以方便的在格网坐标系内进行，为极区的飞机导航、制导及航路规划提供了便利。

除游移方位惯导编排方案外，ECEF坐标系力学编排、惯性坐标系力学编排等多种力学编排方案均可以在极区完成惯导编排解算，通过本文的解决策略均可以获得极区格网航向和格网速度及 ECEF定位坐标。但考虑到惯导系统高度通道的不稳定性，选用游移方位水平坐标编排方案作为解算的内核可以克服此点缺陷，保证纯惯导的长期稳定性。此外，游移惯导编排方案相对而言物理概念清晰、计算量适中，亦在美军机载标准激光捷联惯导标准 SNU-84-1中明确列为必选力学编排方案[11]。

（References）：

[1]Greenaway K R,Gates M D.Polar air navigation-A record[M].Canada:Art Bookbindery,2009.

[2]Vasatka J.Polar operations[EB/OL].[2013-07-7].Http:// www.smartcockpit.com/data/pdfs/flightshops/navigation/ Polar_Operations.pdf.

[3]Gao Xingxin,Heng Liang,Walter T,Enge P.Breaking the ice:Navigating in the arctic[C]//Proc.of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation.Portland,OR,2011:3767-3772.

[4]Yahya M H,Kamarudin M N.Analysis of GPS visibility and satellite-receiver geometry over different latitudinal regions[C]//International Symposium on Geoinformation.Putra World Trade Centre,Kuala Lumpur,Malaysia,2008:1-8.

[5]Berkir E.Introduction to modern navigation systems[M].New Jersey:World Scientific,2007.

[6]Savage P G.Strapdown analytics II[M].Maple Plain,Minnesota:Strapdown Associates,2009.

[7]Department of the Air Force.Air navigation (US.Air Force Pamphlet 11-216)[M].CreateSpace Independent Publishing Platform,2013.

[8]周琪，秦永元，付强文，等.极区飞行格网惯性导航算法原理[J].西北工业大学学报，2013，31(2)：210-217.ZHOU Qi,QIN Yong-yuan,FU Qiang-wen,et al.Grid mechanization in inertial navigation systems for transpolar aircraft[J].Journal of Northwestern Polytechnical University,2013,31(2):210-217.

[9]吴枫，秦永元，周琪.机载武器极区传递对准算法[J].中国惯性技术学报，2013，21(2)：141-146.WU Feng,QIN Yong-yuan,ZHOU Qi.Airborne weapon transfer alignment algorithm in polar regions[J].Journal of Chinese Inertial Technology,2013,21(2):141-146.

[10]周琪.大飞机全球惯性导航算法研究[D].西安：西北工业大学，2013.ZHOU Qi.All-Earth inertial navigation algorithm for large aircraft[D].Xi’an:Northwestern Polytechnical University,2013.

[11]Specification for USAF Standard Form,Fit and Function (F3) Medium Accuracy Inertial Navigation Unit--SNU 84-1,Rev.D[S].Aeronautical Systems Division Air Force Systems Command Wright-Patterson AFB,OH,1992.

Indirect grid inertial navigation mechanization for transpolar aircraft

ZHOU Qi1,2,YUE Ya-zhou1,2,ZHANG Xiao-dong1,2,TIAN Yu1,2
(1.National Key Laboratory on Flight Vehicle Control Integrated Technology,Xi’an 710065 China;2.AVIC Xi’an Flight Automatic Control Research Institute,Xi’an 710065 China)

The indirect grid inertial navigation elements based on wander azimuth mechanization for transpolar flight is presented.First of all,the direction cosine matrix(DCM) from the wander frame to the grid frame is derived.The DCM allows the grid heading and grid velocity be obtained indirectly from wander navigation parameters in high latitude regions,while the heading and velocity are in the manner of truth north heading and geographical velocity from wander navigation parameters in low latitude regions.The earth-centered earthfixed coordinates can be indirectly calculated and directly applicable to aircraft positioning as an alternative to the use of longitude-latitude coordinates in the Polar Regions.Simulation results show that the navigation performance is the same as the direct grid mechanization.The presented approach can solve the polar navigation problems,and the inner mechanization is the same in precision as low latitude inertial navigation elements.

polar navigation;indirect grid navigation;wander azimuth;direction cosine matrix

U666.1

：A

1005-6734(2014)01-0018-05

10.13695/j.cnki.12-1222/o3.2014.01.005

2013-09-26；

：2013-12-27

国家高技术研究发展计划（863计划）（2012AA7053029）

周琪（1984—），男，工程师，工学博士，从事惯性导航及组合导航研究。E-mail：zhouqis@139.com

联 系 人：岳亚洲（1971—），男，研究员，工学博士。E-mail：gnss618@163.com