月面巡视器太阳板对日定向规划算法

刘书豪 彭松

(北京空间飞行器总体设计部, 北京 100094)

月面巡视器太阳板对日定向规划算法

刘书豪 彭松

(北京空间飞行器总体设计部, 北京 100094)

针对月面巡视器太阳板对日定向问题，提出了一种规划算法。分析了规划指标与约束条件，约束条件包括太阳入射角约束和太阳板机械转动约束；推导了在车体姿态不变情况下的定向算法，通过将太阳板运动转换为平面上的矢量旋转，实现对日定向；利用巡视器原地转向运动弥补太阳板单自由度转动的不足，将车体运动与太阳板法向矢量轨迹投影至球面，得到车体原地转向时的定向规划算法。仿真结果表明：文章提出的算法能够实现指定约束下的对日定向；对于无法实现理想对日定向的情况，算法也能够获得太阳板的次优规划。

月面巡视器；太阳板；对日定向；太阳入射约束

1 引言

月面巡视器是实现对月球近距离考察的重要途径[1-2]。太阳板为月面巡视器提供能源，目前与之类似的太阳翼已经在地球轨道卫星上得到大量应用，国内外也针对太阳翼及其驱动技术开展了大量研究。文献[3]分析了太阳翼技术发展趋势，文献[4]从控制器设计角度探讨了太阳翼机构的定向控制，文献[5]详细分析了各种工况下的卫星太阳翼光照角度计算模型，文献[6]针对倾斜轨道航天器提出惯性定向和对地定向两种航天器太阳翼对日跟踪的若干算法，文献[7]提出双自由度驱动机构的轨迹规划算法，文献[8-9]通过合适的起始时刻驱动太阳翼匀速旋转，保证太阳翼法线和太阳光线的夹角保持最佳位置。上述文献解决问题的思路基本一致，均根据卫星轨道与太阳位置的几何关系来计算太阳翼转动。但是，月面巡视器与地球轨道卫星在太阳翼的应用形式上存在较大差异，具体表现在：一方面，对于地球轨道卫星，为了获得充足的能源，应保证太阳矢量与太阳翼法线夹角最小，达到最佳的太阳光照状态；但对于月面巡视器而言，其在月面着陆后，将经历长时期恶劣的月球环境，过强的光照状态可能会对热控等系统产生不利影响，进而影响巡视任务[10-11]，考虑到能源供应与热控条件的双重约束，应保证巡视器太阳板的太阳入射角满足一定的角度约束。另一方面，大多数地球轨道卫星很少通过调整星体姿态达到提高太阳光照的目的；但月面巡视器可通过调整车体姿态获得更合适的光照，这大大增加了巡视器对日定向的灵活性。

针对上述两点，目前国内几乎没有文献开展相关研究。本文针对巡视器的特点，考虑了太阳入射角约束、机构运动约束等条件，提出了一种对日定向的规划算法。由于运动规划结果与巡视器姿态密切相关，本文分别对车体姿态固定、车体原地转向两种工况进行分析，可用于月面巡视器系统任务设计与仿真验证。

2 定义与约束

(1)巡视器本体坐标系：X轴位于结构底板对月面内，+X轴指向巡视器前进方向；Z轴沿结构底板对月面法线方向，+Z轴指向月面；Y轴与Z轴和X轴构成右手坐标系。坐标系定义如图1所示。

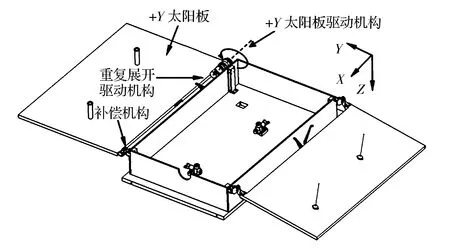
图1 巡视器坐标系

(2)太阳入射角φ：太阳方向矢量与+Y太阳板平面法线矢量的夹角。

(3)+Y太阳板运动：+Y太阳板指位于本体坐标系+Y侧的太阳板。巡视器在月面巡视过程中，只有+Y太阳板具有运动自由度，因此只针对+Y太阳板开展研究。在巡视器本体坐标系下，太阳板处于收拢压紧状态时，基板平面与XOY面平行的位置为太阳板的零位，如图2所示。在巡视器本体坐标系下，+Y太阳板具有一个自由度，其转轴的正方向与巡视器的+X轴指向相同，然后按右手法则确定转角的正负。+Y太阳板转角θ可限制在图2所示的红色阴影区域内，该区域张角记为Δ，Δ∈(0°,90°)。

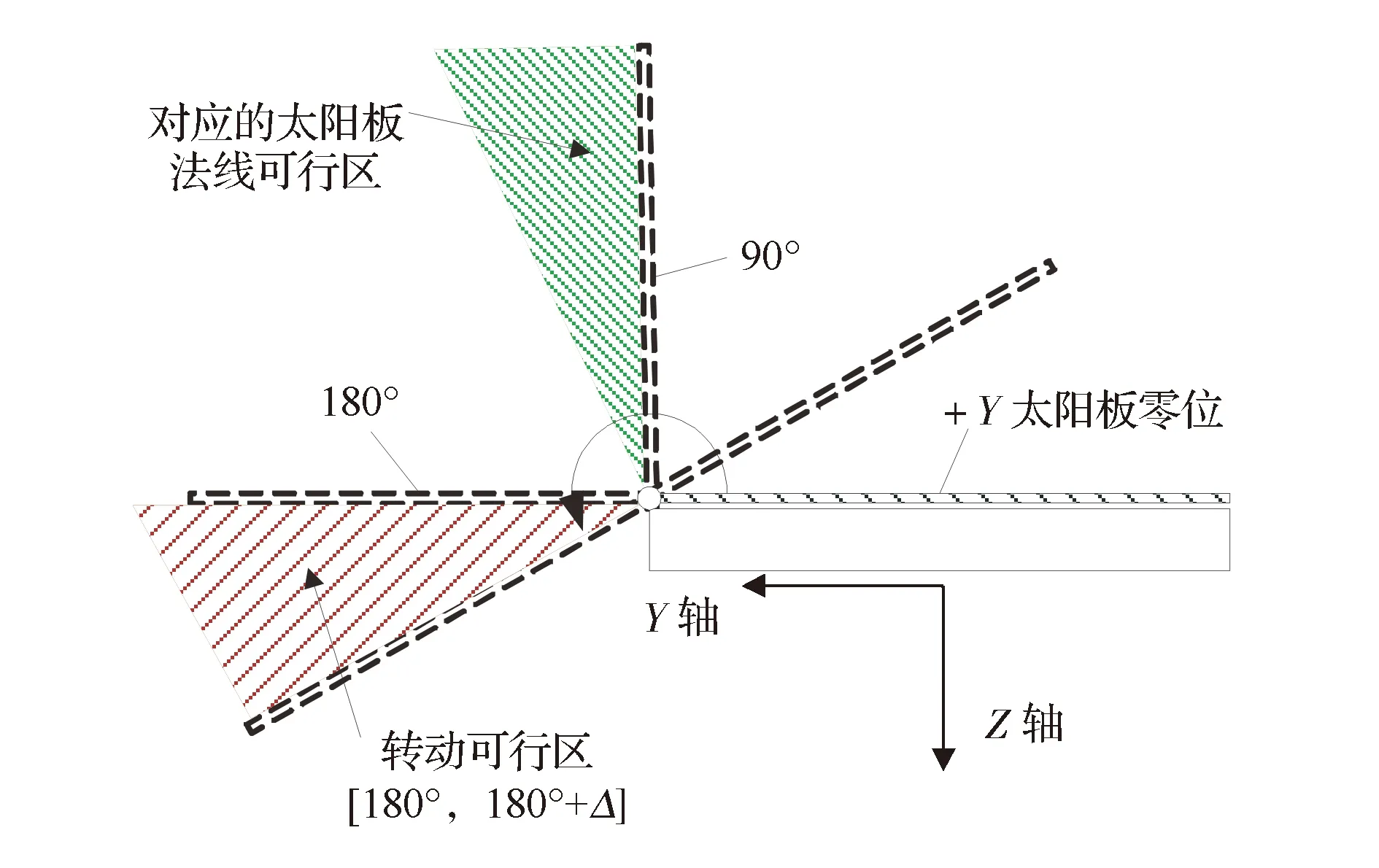
图2 +Y太阳板转动定义

3 车体姿态固定时的对日定向规划算法

3.1规划目标

根据车体位置、姿态信息，计算+Y太阳板对日定向时所需的太阳板转角θ，使得太阳板处于最优光照条件，同时满足如下约束。

(1)太阳入射角约束：为了适应热控的需要，太阳入射角φ应满足φ≥Ω，其中，Ω为固定常值，代表了太阳入射角的可达最优状态。

(2)太阳板运动范围约束：当太阳板展开角度小于180°时，太阳板会对巡视器车体设备产生遮挡，因此本文要求太阳板转角θ满足θ∈[180°,180°+Δ]，对应的太阳板转动可行范围如图2中红色阴影区域所示。

3.2问题分析

设太阳板转角θ对应的规划太阳板法向矢量为P，太阳板对日定向规划问题实质为太阳板法向矢量的求解问题。不难发现，太阳板法向始终处于巡视器本体坐标系的YZ平面内。考虑到太阳板转动范围限制在图2所示的红色阴影区域内，因此，不考虑原地转向时，太阳板对日定向问题实际上可转换为在YZ平面红色阴影区域内的矢量求解问题。算法基本思路为：首先计算无入射角约束下太阳板的最优光照状态；然后对最优状态进行约束检查；最后得到可行太阳板转角θ，如果存在两个解均满足对日定向要求，则选取转动幅度最小的转角作为规划解。

3.3算法说明

假设太阳矢量S在巡视器本体坐标系下的投影Sb的坐标为(sb，x，sb，y，sb，z)T，进而可得其在YZ平面的投影Sb_pro的坐标为(0，sb，y，sb，z)T。定义太阳矢量与巡视器本体坐标系YZ平面的夹角为φ0，则

(1)

显然，如果不考虑太阳入射角约束和太阳板运动范围，则φ0代表了太阳板所能达到的最优光照状态。下面将根据φ0的取值，分几种情况确定可行的太阳板法线矢量。

1)φ0=90°

这代表了一种极限情况，表明太阳板对光照不可见；此时，无论太阳板如何旋转，也无法接收太阳光。

2)Ω≤φ0<90°

此种情况如图3所示，太阳入射角也无法达到Ω，则φ0为太阳入射角的可达最优状态。与φ0对应的太阳板法向矢量Sb_pro，即为所求的太阳板法向矢量P，进而可得对应的太阳板转角θt为

(2)

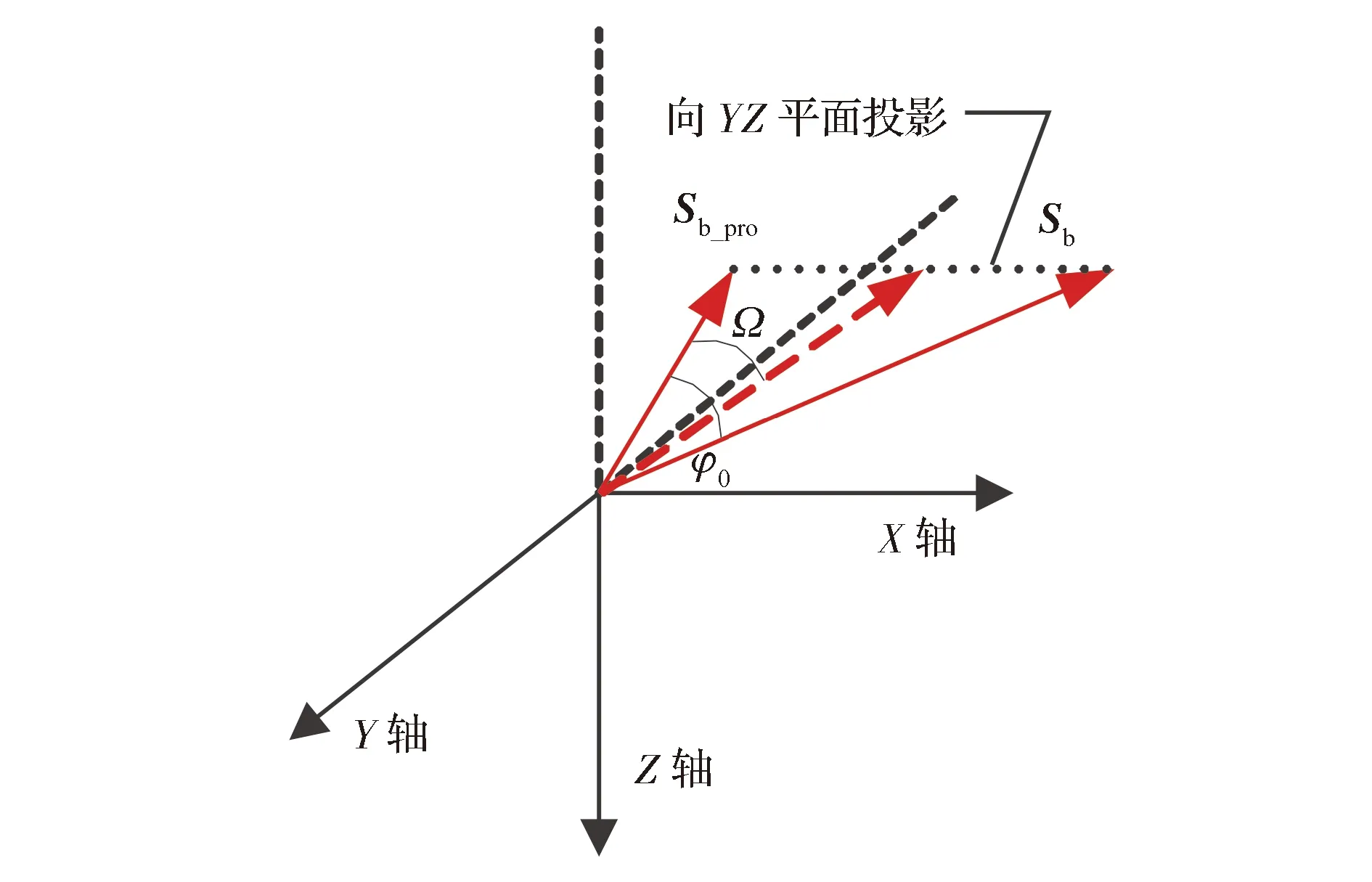
图3 Ω≤φ0<90°几何关系示意

上述过程保证了太阳入射角满足约束，还要对太阳板运动约束进行检查。若180°<θt<Δ+180°，则规划得到的太阳板转角为θ=θt；否则，表明θt超出了太阳板运动范围的限制，不可行，取θt转动幅度最小的极限位置作为规划结果。

3)φ0<Ω

如图4所示，O为巡视器本体坐标系原点，太阳板理想对日定向后，φ0<Ω，不满足约束要求，此时可将太阳板法向偏离太阳投影矢量一定的角度α，使所求得的矢量P1，P2与太阳光夹角为Ω。因此，问题最终转换为求解矢量P1和P2，进而判断矢量对应的太阳板转角是否满足转动约束即可。

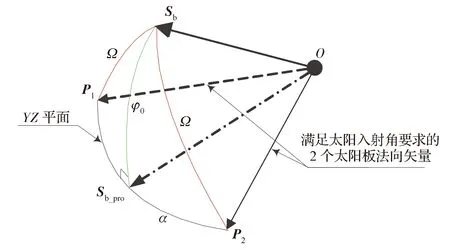
图4 2个可行法向矢量示意

从图4中可看到，Sb，Sb_pro，P1在球面的投影点构成了球面直角三角形，根据球面几何可得

(3)

将矢量Sb_pro绕X轴分别旋转角度α和-α，可得法线矢量的2个解P1和P2，进一步可求得对应的太阳板转角θ1和θ2，求解方法同式(2)。

最后，判断θ1和θ2是否满足运动限制，判断规则如下。

(1)如果θ1,θ2∉(180°,180°+Δ)，设当前太阳板转角为θ0，如果|180°-θ0|<|(180°+Δ)-θ0|，则规划的太阳板转角为θ=180°，否则，θ=180°+Δ；

(2)如果θ1∉(180°,180°+Δ)，θ2∈(180°,180°+Δ)，则规划的太阳板转角θ=θ2；

(3)如果θ1∈(180°,180°+Δ)，θ2∉(180°,180°+Δ)，则规划的太阳板转角θ=θ1；

(4)如果θ1,θ2∈(180°,180°+Δ)，那么令Δθ1=min[|180°-θ1|,|(180°+Δ)-θ1|]，Δθ2=min[|180°-θ2|,|(180°+Δ)-θ2|]，如果Δθ1<Δθ2，则规划的太阳板转角为θ=θ1，否则，θ=θ2。

4 车体原地转向时的对日定向规划算法

利用第3节算法无法达到太阳入射角设计值Ω时，可考虑利用巡视器绕本体坐标系Z轴的原地转向功能，使太阳板达到较为理想的光照状态。本节将对这一问题进行探讨。

4.1规划目标

本节规划目标与第3.1节类似，区别在于增加了车体原地转向的自由度。规划的指标为太阳板法向在空间的运动幅度最小，同时满足太阳入射角约束和太阳板运动约束。

需要说明的是，由于地形的起伏，原地转向过程可能会对俯仰、滚动姿态造成影响[12-13]，这类影响无法通过几何手段建模，本文假设巡视器位于较为理想的水平面或斜面上。

4.2问题分析

增加车体运动的自由度后，太阳板法向矢量可在以Z轴为对称轴的圆锥上运动，圆锥半张角为Δ。如图5所示，记-Z轴在天球上的投影点为Zminus，将太阳矢量S投影到巡视器本体天球，投影点记为S，则满足太阳入射角为Ω的法向矢量构成了以点S为圆心、半径大小为Ω的球面圆(图5阴影所示)，该圆的圆周记为⊙S；记初始太阳板法向矢量为P0，它在巡视器本体天球上的投影点记为P0。如果能在球面圆S的边界找到距离P0最近的点Ps，那么点Ps对应的矢量即为待求的太阳板法向矢量，进而可求出对应的车体原地转向角与太阳板转角。

4.3算法说明

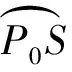
(4)

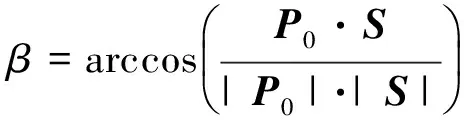
(5)

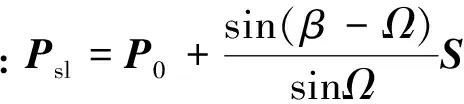
法线矢量Pcross与-Z轴的夹角ε，以及太阳矢量S与-Z轴的夹角λ，计算公式如下。

(6)

(7)

式中：-Zaxis为单位矢量，其方向为本体坐标系Z轴的负方向。

图5中包括考虑原地转向时的3种几何关系示意。下面根据ε进行具体判断。

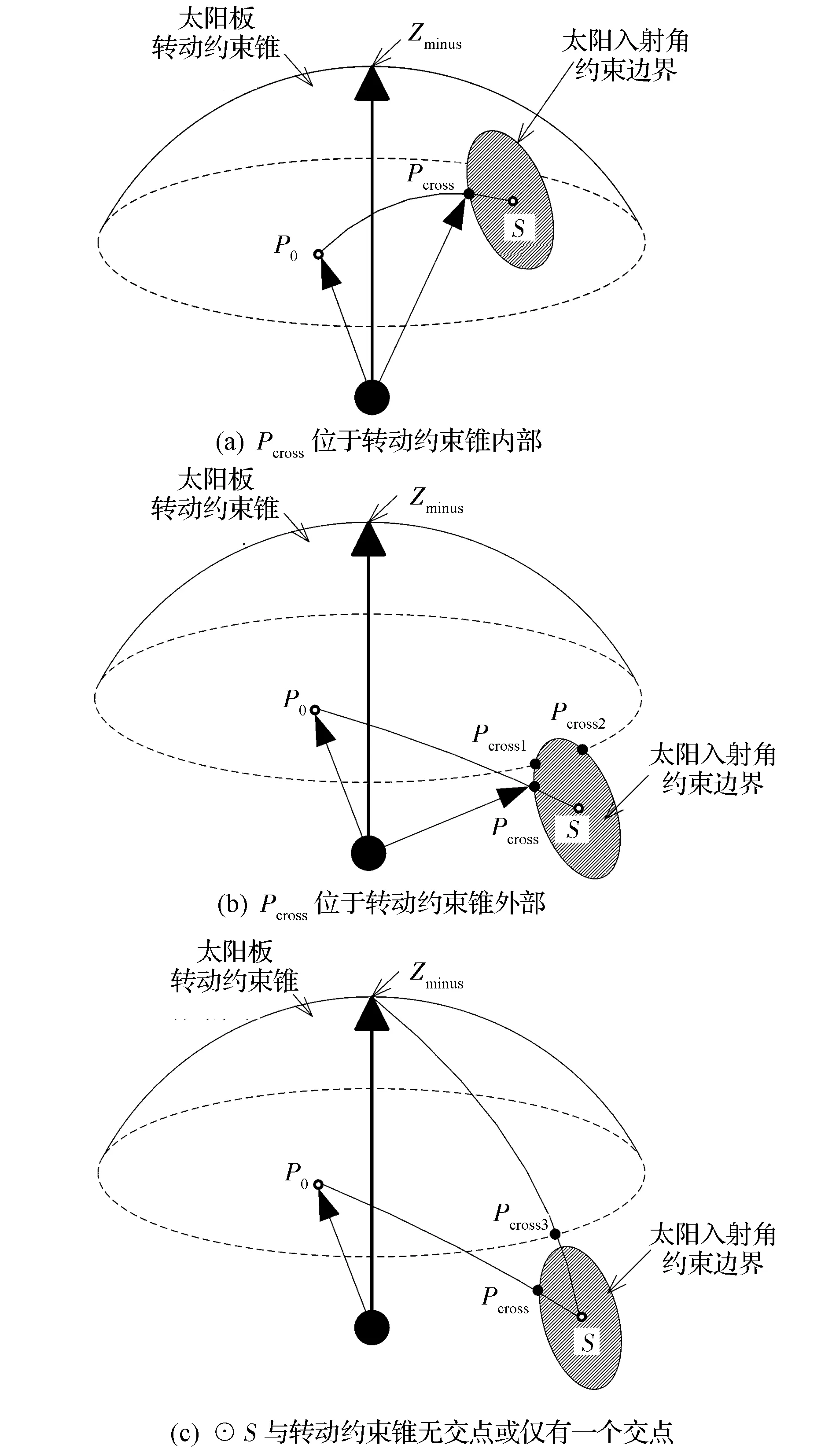
图5 考虑原地转向时几何关系示意

1)ε≤Δ

对应图5(a)。Pcross位于太阳板转动约束锥内部，表明车体可通过原地转向和太阳板旋转达到该位置，Pcross即为规划的太阳板法向矢量。记Pcross在本体坐标系投影的坐标为(px,py,pz)T，则所需的太阳板转角θ与原地转向角ρ为

(8)

(9)

2)ε>Δ，且λ<Δ+Ω

对应图5(b)。Pcross位于转动约束锥外部，且⊙S与转动约束锥存在2个交点。令转动约束锥与⊙S的交点分别为Pcross1和Pcross2，对应的矢量记为Pcross1和Pcross2，则太阳板法线矢量位于Pcross1或Pcross2时将达到最优光照状态，可从中选择与P0夹角最小的矢量作为规划结果。因此，问题归结于求取交点Pcross1和Pcross2及其对应的矢量。

将Zminus，S，Pcross1连接，可构成球面三角形，如图6所示。

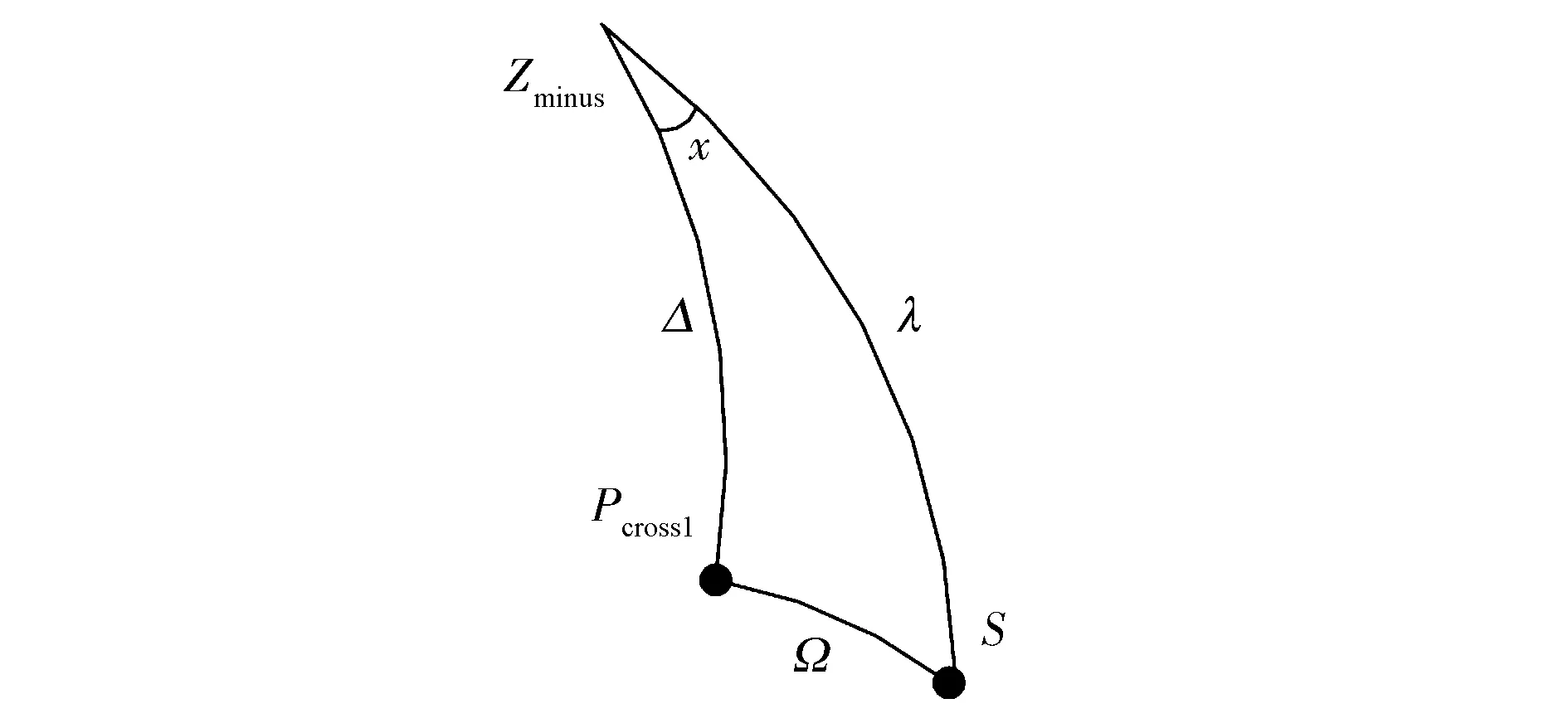
图6 球面三角形Pcross1ZminusS

根据球面三角形的余弦定理，记ZminusPcross1和ZminusS的夹角为x，可表示为

(10)

分别计算Pcross1，Pcross2与P0的夹角，取夹角最小的矢量作为规划的太阳板法向矢量，从而可得所需的太阳板转角与原地转向角，计算过程同式(8)和式(9)。

3)λ≥Δ+Ω

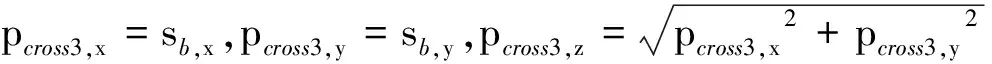
5 仿真算例

为分析上述算法的有效性，选取三类场景仿真。首先，利用美国喷气推进实验室(JPL)的DE405星历计算太阳方位，并将其转换至巡视器本体坐标系下；然后，根据期望的光照状态，利用本文算法对太阳板转动进行规划；最后，计算按规划结果转动后太阳板法向矢量与太阳光的夹角，判断太阳板光照状态是否满足指标要求。假设太阳板转动范围为[180°，210°]，应满足的最小太阳入射角不小于20°，即Δ=30°，Ω=20°。

场景一：仿真时间为北京时间2013年9月19日12：00，假设巡视器位于月面(10.5°W，20.1°N)，巡视器本体坐标系与当地北东地系重合，得到太阳矢量在本体坐标系投影的坐标为(-0.341 132，0.329 058，-0.880 539)T。根据投影数据，采用本文给出的车体姿态固定时对日定向规划算法进行求解，得到太阳板转角为198.98°；然后，利用该转角规划结果，计算得到法向矢量与太阳光夹角为20°，表明规划结果能够满足任务要求。

场景二：仿真时间为北京时间2013年10月17日00：50，巡视器位置、坐标与场景一相同，得到太阳矢量在本体坐标系投影的坐标为(-0.255 3，0.687 6，-0.679 6)T。根据投影数据，采用车体姿态固定时的对日定向规划算法求解，得到太阳板转角规划值为210°；利用该规划结果，计算法向矢量与太阳光夹角为21.19°，表明无法满足任务要求，此时可考虑调整车体姿态以优化太阳板光照状态。考虑原地转向后，本文算法得到的太阳板转角为207.189°，原地转向角为20.37°，进而得到太阳板法向矢量与太阳光夹角为19.99°，表明原地转向后，太阳板的太阳入射角可满足20°的要求。

场景三：仿真时间为北京时间2013年10月16日02：00，巡视器位置、坐标与场景一相同，得到太阳矢量在本体坐标系投影的坐标为(-0.203 462，0.819 269，-0.536 098)T。根据投影数据，采用车体姿态固定时对日定向规划算法求解，得到太阳板转角为210°；利用该结果计算得到法向矢量与太阳光夹角为29.08°，表明仅转动太阳板无法满足光照要求，此时可考虑调整车体姿态以优化太阳板光照状态。考虑原地转向后，本文算法得到的太阳板转角为210°，原地转向角为13.943 9°，进而得到太阳板法向矢量与太阳光夹角为27.58°，表明原地转向后，太阳板的太阳入射角最优仅能达到27.58°，与20°的目标角度尚存在差距。

6 结束语

本文针对月面巡视器太阳板的入射角约束和机械转动约束，分析了车体姿态固定和车体原地转向时太阳板法向矢量与太阳光的空间几何关系，将对日定向问题分别投影至一维平面和二维球面求解，得到了太阳板运动的规划算法。三个仿真场景分别对应三类典型的空间几何关系，表明算法对各类工况处理的有效性。本文算法可用于月面巡视器在轨任务规划的设计、验证与分析。在推导原地转向太阳板规划算法的过程中，没有考虑地形引起的俯仰和滚动方向姿态变化，由于地形起伏具有一定的随机性，后续将对此开展深入研究。

References)

[1]贾阳，陈建新，张熇.月面巡视探测器关键技术分析[J].航天器工程，2006，15(3):16-22

Jia Yang， Chen Jianxin， Zhang He. Key technology analysis of lunar rover[J]. Spacecraft Engineering, 2006, 15(3):16-22 (in Chinese)

[2]李群智，宁远明，申振荣，等.行星表面巡视探测器遥操作技术研究[J].航天器工程，2008，17(3):29-35

Li Qunzhi， Ning Yuanming， Shen Zhenrong， et al. Study on teleoperation of rover on planetary surface[J]. Spacecraft Engineering，2008，17(3):29-35 (in Chinese)

[3]Michael Piszczor．Trends in solar array technology development[C]//Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, 2001. Washington D.C.：AIAA，2001：1-6

[4]Ali H ALmukhtar. Design of phase compensation for solar panel systems for tracking sun [C]//Proceedings of the TerraGreen 13 International Conference 2013-Advancements in Renewable Energy and Clean Environment. Amsterdam： Elsevier Ltd.，2013：9-23

[5]陈忠贵，张志，廖瑛.航天器太阳翼在轨光照角度建模及仿真分析[J].航天器工程，2012，21(1):35-39

Chen Zhonggui，Zhang Zhi，Liao Ying. Modeling and simulation analysis of solar illumination angle on spacecraft solar wing in-orbit[J]. Spacecraft Engineering，2012，21(1)：35-39 (in Chinese)

[6]王颖, 顾荃莹. 倾斜轨道航天器太阳翼对日跟踪方法探讨[J], 航天器工程, 2009, 18(3):36-40

Wang Ying, Gu Quanying. Methods of solar array tracking for inclined-orbit satellite[J]. Spacecraft Engineering, 2009，18(3):36-40 (in Chinese)

[7]陶溢, 潘存云, 谭颖琦. 一种提高太阳能帆板受晒效率方法[J]. 上海航天, 2007, 24(5):23-26

Tao Yi, Pan Cunyun, Tan Yingqi. A method to improve sunshine efficiency of solar array[J]. Aerospace Shanghai, 2007, 24(5):23-26 (in Chinese)

[8]翟坤，杨涤，陈新龙，等. 太阳同步轨道卫星的太阳帆板驱动律[J]. 上海航天, 2009, 26(1):20-23

Zhai Kun, Yang Di, Chen Xinlong,et al. Study on driving laws of sun synchronous orbit satellite’s solar arrays[J]. Aerospace Shanghai, 2009, 26(1):20-23 (in Chinese)

[9]朱军年. 太阳同步轨道卫星帆板对日定向控制与仿真[J]. 计算机仿真, 2011, 28(3):110-114

Zhu Junnian.Simulation of sun synchronous orbit sate-llite solar panel control[J]. Computer Simulation, 2011, 28(3):110-114 (in Chinese)

[10]EgonsRPodnieks,JohnASiekmeier.Miningtechno-logyforlunarresourceutilization[R].Minneapolis：USDepartmentoftheInteriorBureauofMines, 1990

[11]任德鹏, 贾阳, 刘强. 月面巡视探测器太阳帆板热电耦合仿真计算[J]. 航天器环境工程, 2007, 24(5):278-282

RenDepeng,JiaYang,LiuQiang.Calculationofthermoelectriccogenerationonthesolarpanelsofalunarrover[J].SpacecraftEnvironmentEngineering, 2007, 24(5):278-282 (inChinese)

[12]张玥, 李清毅, 许晓霞. 月球表面地形数学建模方法[J]. 航天器环境工程, 2007, 24(6):341-343

ZhangYue,LiQingyi,XuXiaoxia.Mathematicalmodelingoflunarsurfaceterrain[J].SpacecraftEnvironmentEngineering, 2007, 24(6):341-343 (inChinese)

[13]李清毅. 巡视器对地指向受月表地形的影响分析[J]. 中国空间科学技术, 2009, 29(6):39-44

LiQingyi.Influencesanalysisofmoonsurfaceterrainontheroverantennadirection[J].ChineseSpaceScienceandTechnology, 2009, 29(6):39-44 (inChinese)

(编辑：夏光)

Algorithm for Solar Panel Direction Planning of Lunar Rover

LIU Shuhao PENG Song

(Beijing Institute of Spacecraft System Engineering, Beijing 100094, China)

For directing to the sun of the lunar rover’s solar panel, an algorithm based on planning method is proposed. Firstly, the goal and constraints are introduced. Constraints contain the sunlight incident angle and the solar panel rotation limits. Secondly, a planning with the rover’s attitude preserved is researched. The panel motion is transferred into the vector rotation in a plane, which makes the planning easier. Thirdly， the planning considering zero radius steering is investigated, by projecting the motion of the rover and solar panel into rover body coordinate sphere. The additional rover freedom is helpful to direct to the sun. Finally, computer simulation results show that the proposed algorithm can achieve directing to the sun with specified constraints and a suboptimal planning can be acquired for the case of not ideally directing to the sun.

lunar rover; solar panel; directing to the sun; sunlight incident constraint

2013-08-01；

：2013-10-23

国家重大科技专项工程

刘书豪，男，工程师，研究方向为航天器总体仿真技术。Email:33151420@163.com。

V467.3

：ADOI：10.3969/j.issn.1673-8748.2014.03.008