Liouville 在分数阶微积分概念方面的研究

张文芳

(西北大学数学与科学技术史研究中心,陕西西安710127)

Liouville 在分数阶微积分概念方面的研究

张文芳

(西北大学数学与科学技术史研究中心,陕西西安710127)

分数阶微积分的概念是以整数阶微积分理论研究为基础,而分数阶微积分概念的建立经历了漫长的过程.探析此过程中数学家在研究分数阶微积分理论方面的贡献,进而整理Liouville在分数阶微积分概念方面的研究,进一步概括分数阶微积分第一定义的由来以及为后续相关研究奠定的坚实基础.

整数阶微积分;分数阶微积分;刘维尔定义

1 引言

所谓分数阶微分和积分运算(fractional derivatives and integrals),是指微分的阶数和积分的次数不是整数,它可以是任意实数,乃至复数.分数阶微积分的提出和发展与整数阶微积分的发展有着密不可分的关系,且已发展成为一重要的数学分支并被广泛应用于实际问题中.由此可知,分数阶微积分概念的形成过程是至关重要的,细数在此过程中做出相关贡献的数学家,其中Liouville的理论研究以及实际应用是不可或缺的,甚至对分数阶微积分概念的形成及发展有着深远的影响.

2 Fourier和Abel的相关贡献

自1695年,Leibniz与L.Hospital以通信的方式提出“如果将整数阶的微分推广到分数阶的微分,那么分数阶微分的意义是什么呢”[1]?这一问题,在Euler,Lagrange,Laplace,Lacroix等先驱富有竞争性的探索基础上.1822年,Fourier推导出任意阶微分的Fourier定义:如果

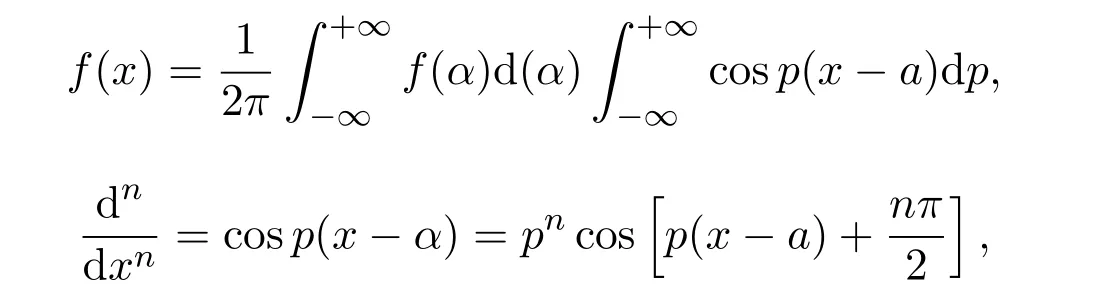
此处α,p为积分因子,n为整数,则对任意数µ,得[2-3]:

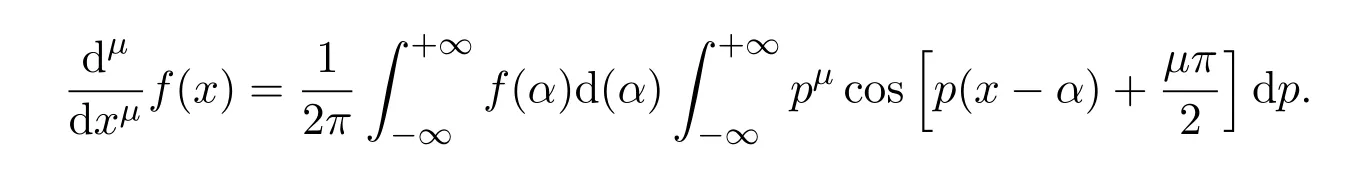
并且他描述到:“上述提及的µ,将可以看作是任意数,不论是正的或者负的”.1823年,Abel在求解一个积分方程的过程中用到了分数阶微积分,在这个问题中,假设滑动次数

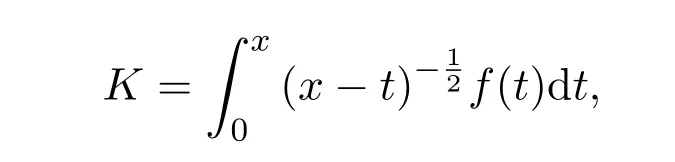
被积函数f(t)是未知的,有待确定的,获得了[4]:

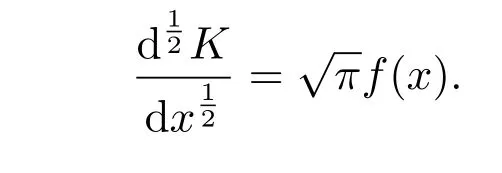
到这一时期,对于分数阶微分的含义,已经有了最初的模糊表达.

3 Liouville的贡献

Liouville受Fourier定义与Abel应用的启发,于1832年提出分数阶导数第一个较为合理的定义.指出对于整数阶的导数:

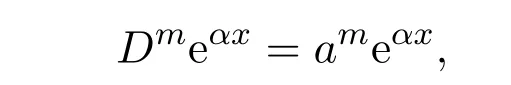
将其推广到任意阶导数可得:

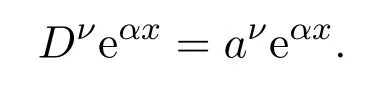
假设函数f(x)存在任意阶导数,并且可将其展成级数形式

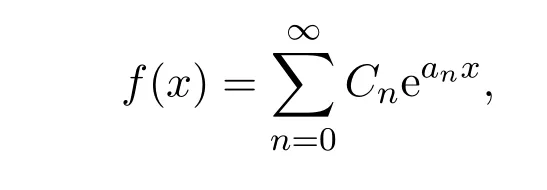
从而[5]

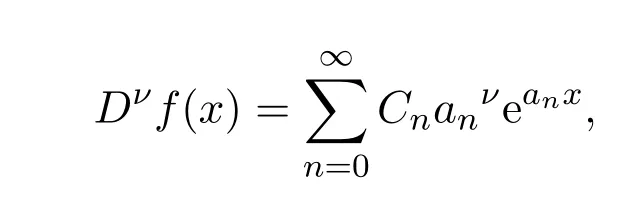
综上,是Liouville关于分数阶导数的第一个定义的具体释义.是否可以将阶数ν推广为有理数、无理数或者是复数?显然存在问题:ν必须选自使得级数连续的自变量的集合.为解决此问题,他从与欧拉Gamma积分有关的定积分

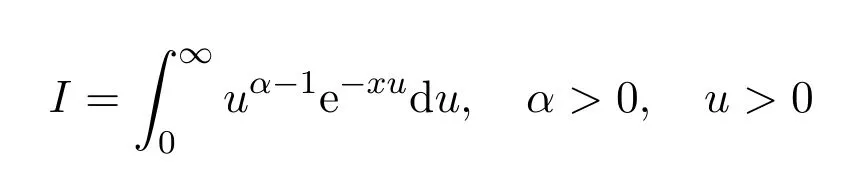
着手研究,替换变量xu=t,得

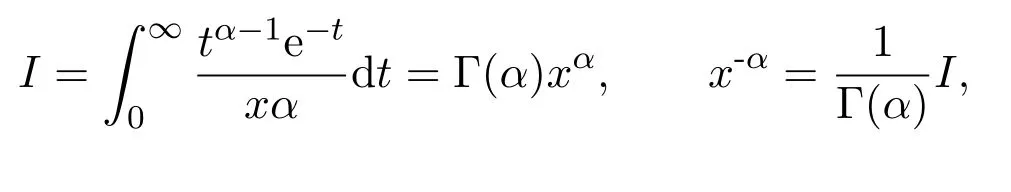
对其两端求ν阶导数,得

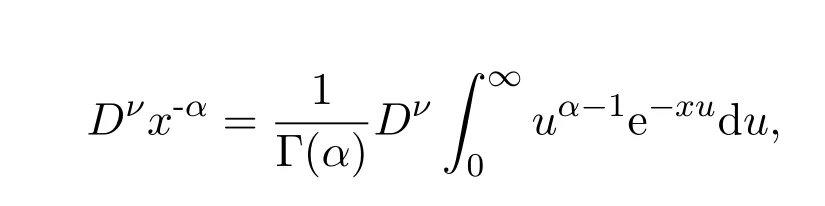
关于x的任意阶导数,按照Liouville的基本假设,得

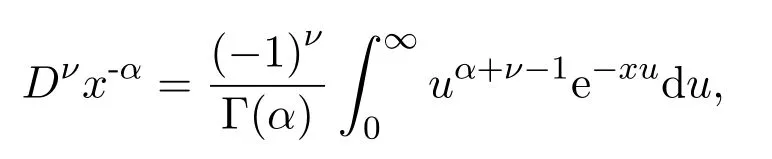
作如上变换,得[6]:

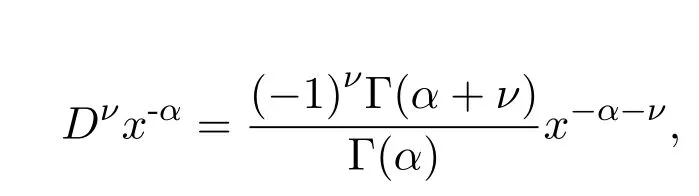
得到Liouville关于分数阶导数的第二个定义.

在第一个定义式中,ν被限制在使得级数连续的自变量的集合中;而在第二个定义式中,仅对xα型的函数适用,不适合应用于更广泛的函数类[7],虽然他的定义都因其本身的局限性而未得到广泛的应用,但是Liouville给出的是分数阶微积分概念形成中第一个较为合理的定义,它对于该概念的最终确立有着奠基作用.

4 Riemann-Liouville定义的形成

1847年,Riemann在此基础上,对分数阶微积分的定义又作了进一步的补充.Riemann寻找了一个广义的泰勒级数,并且导出[8]

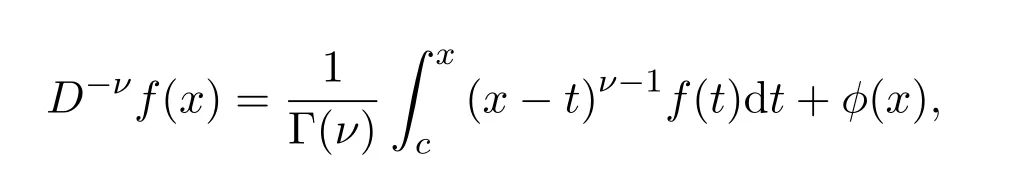
由于积分下限是模糊不清的,在定义中添加适合的余函数ϕ(x),这个余函数的本质是提供一种偏离指数定律的运算方法,比如,

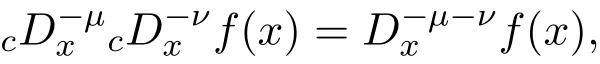
1890年,他从欧拉积分公式

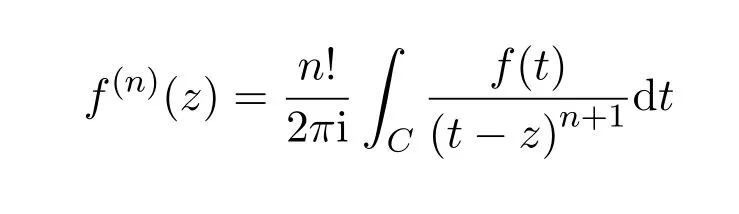
着手,得

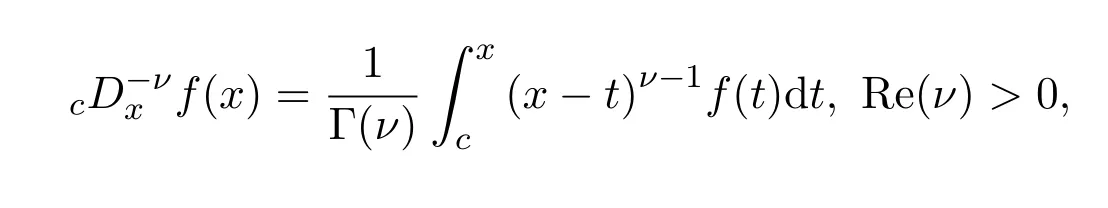
若以−ν代换ν,即有运用连续解析函数,得

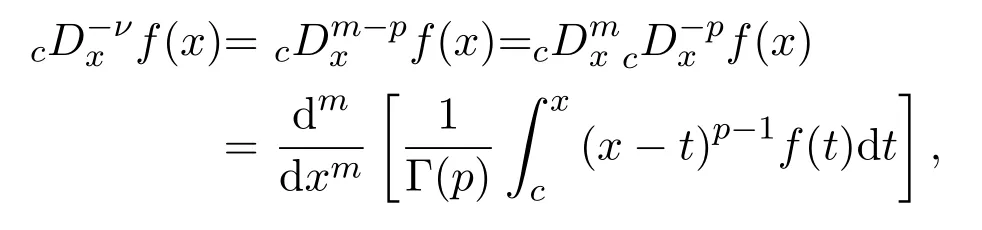
其中

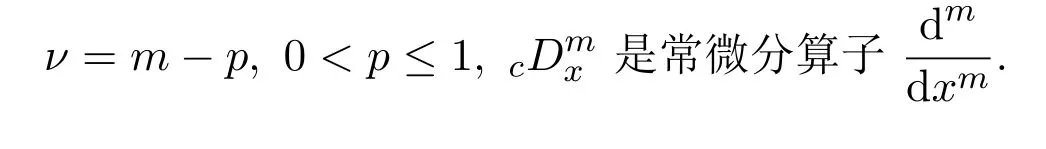
当

c=0或者c=∞,f(x)=xα及f(x)=x−α(α>0,Re(ν)>0),

获得了Riemann-Liouville积分与微分定义:

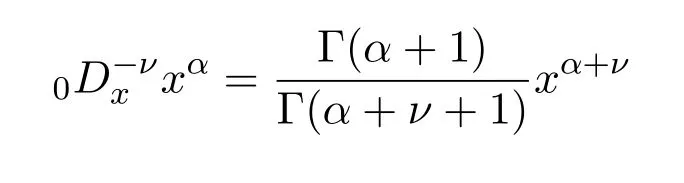
与

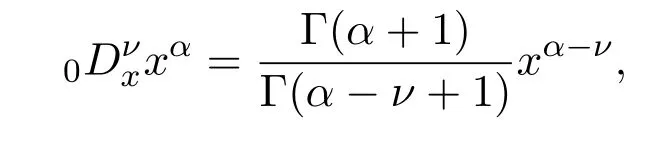
及[9-10]

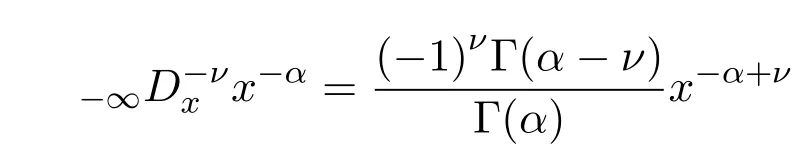
与

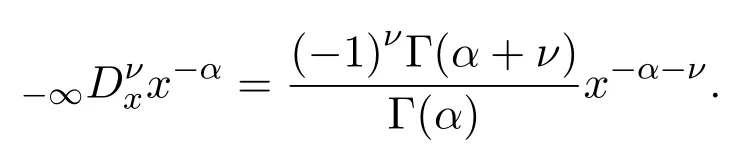
从而形成了第一个较为完整的Riemann-Liouville分数阶微积分的定义.

5 结论

由于分数阶微积分缺乏相关几何物理意义的支撑,发展相对缓慢,数学家也仅仅是在理论上进行探索.Abel在等时问题中涉入了分数次运算,在一定程度上激发了数学家对分数阶微积分研究的热情.于是Liouville提出第一个分数阶微积分的定义,并将其应用于位势理论中,使得分数阶微积分的概念不仅在理论上逐渐趋于完善,而且在实际中也有一定应用.基于此, Riemann及后期数学家得到了运用较为普遍的Riemann-Liouville分数阶微积分定义.

[1]Leibniz G W.Leibniz an del′Hospital In Deuvres Math´ematiques de Leibniz.Correspondance de Leibniz avec Hugens,van Zulichem et le Marquis de L′Hospital[M].Pair:Libr.de A.Franck,1853.

[2]McBride S,Roach G F.Fractional Calculus[M].Glasgow:University of Stratchelyde,1985.

[3]Podlubny I.Fractional Di ff erential Equations[M].San Diego:Academic Press,1999.

[4]Abel N H.Solution de quelques probl`emes`e l′aide d′int´egrales d´e fi nies[J].Oeuvres Compl`etes,1881,1:16-18.

[5]Ross B.Brief History and Exposition of the Fundamental Theory of Fractional Calculus,Lecture Notes in Math[M].New York:Spring-Verlag,1975.

[6]Ross B.The development of fractional calculus 1695-1900[J].Historia Mathematica,1977,4:76-80.

[7]Liouville J.M´emoire sur quelques qu´estions de g´eometric et de m´ecanique,et sur un noveau genre pour r´esoudre ces questions[J].J.´Ecole Polytech,1832,13:1-69.

[8]Miller K S,Ross B.An Introduction to the Fractional Calculus and Fractional Di ff erential Equations[M]. New York:John Wiley&Sons Inc.,1993.

[9]Samko S G,Kilbas A A,Marichev O I.Fractional derivatives and integrals:Theory and Applications[M]. New York:Gordon and Breach,1993.

[10]Keith B O,Spanier J.Fractional Calculus:Theory and Applications,Di ff erentiation and integration to Arbitrary Order[M].New York:Academic Press,1974.

Liouville′s studies in terms of the concept of fractional calculus

Zhang Wenfang

(Center for the History of Mathematics and Sciences,Northwest University,Xi′an710127,China)

The concept of factional calculus is based on calculus theory,while the establishment of the concept of factional calculus has experienced a long process.We explore the contribution that mathematicians had made on the study of the theory of fraction calculus.And combine Liouville’s studies in terms of concept of factional calculus.Then we can generalize the origin of the fi rst de fi nition of the factional calculus and lay a solid foundation to the further research.

calculus,factional calculus,the de fi nition of Liouville

O172

A

1008-5513(2014)01-0100-05

10.3969/j.issn.1008-5513.2014.01.015

2013-12-10.

张文芳(1987-),硕士生,研究方向：近现代数学史.

2010 MSC:34B24