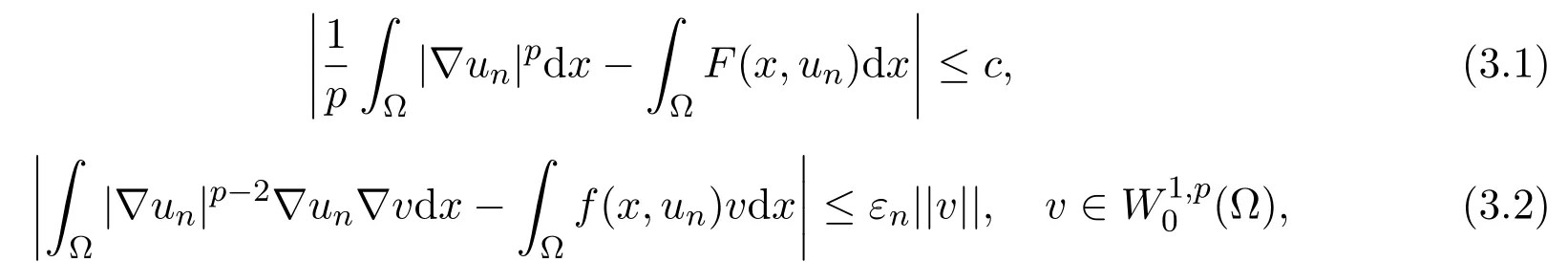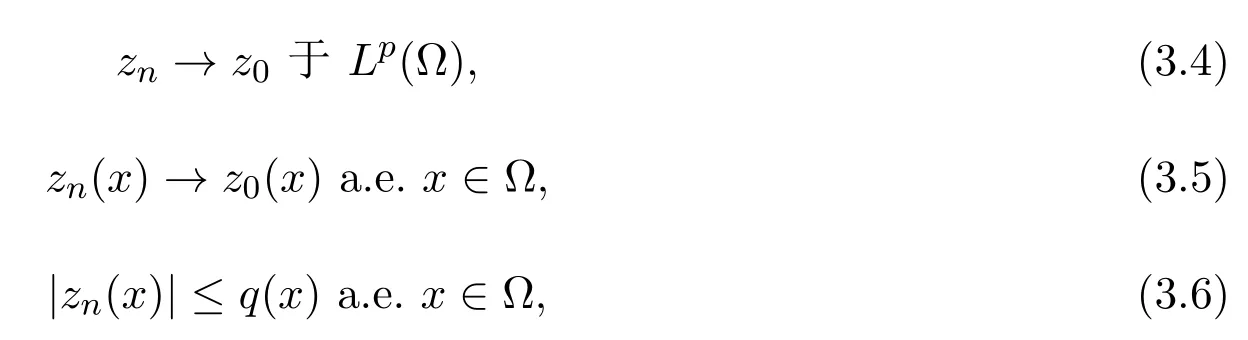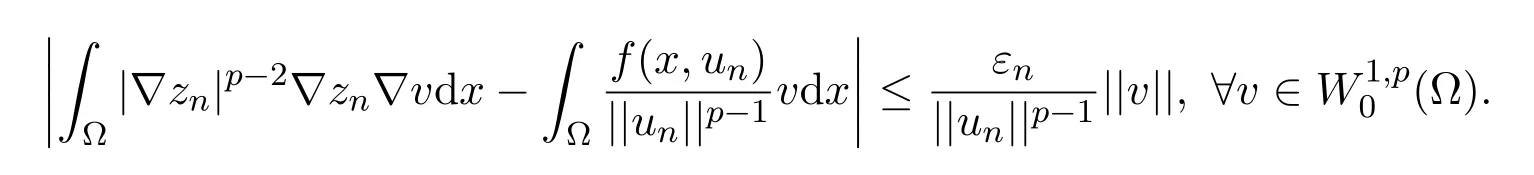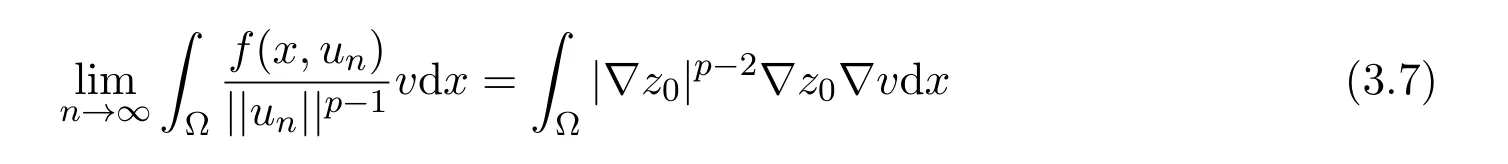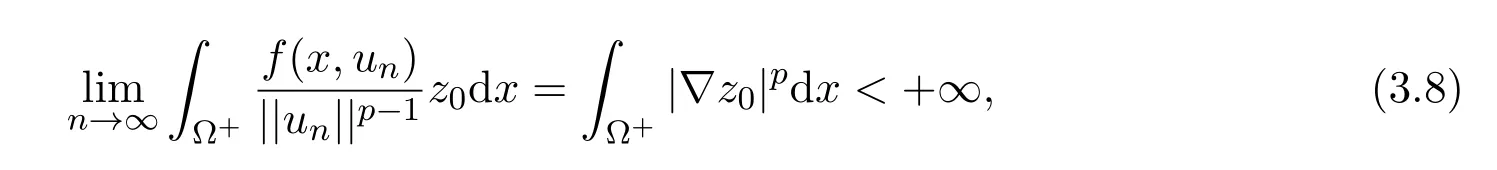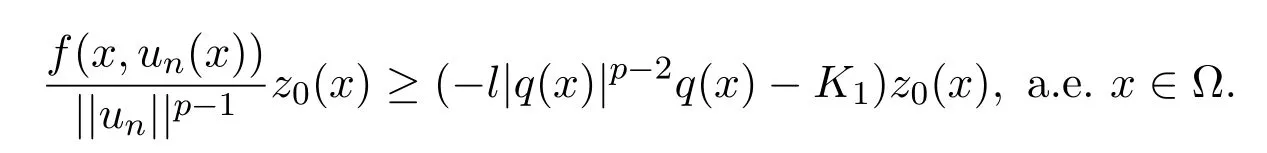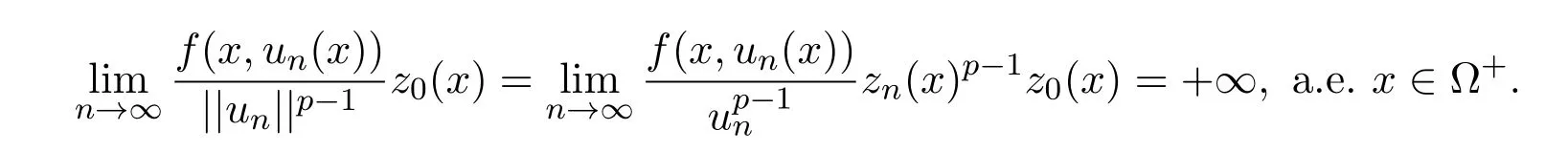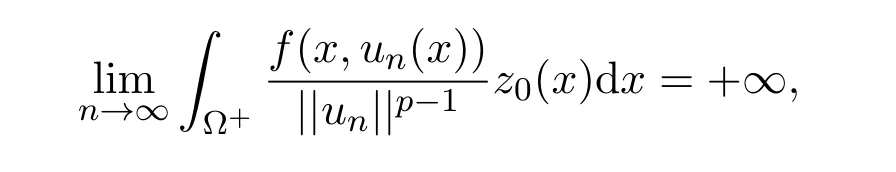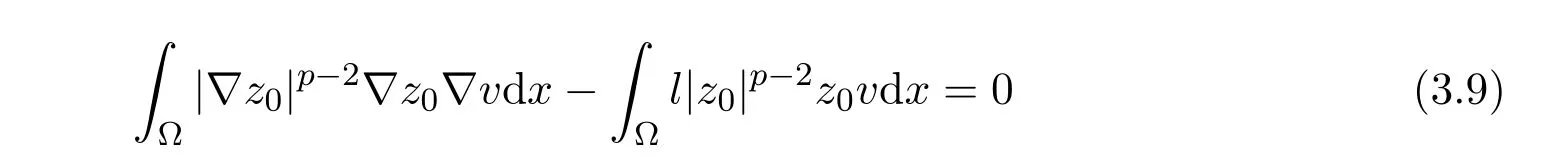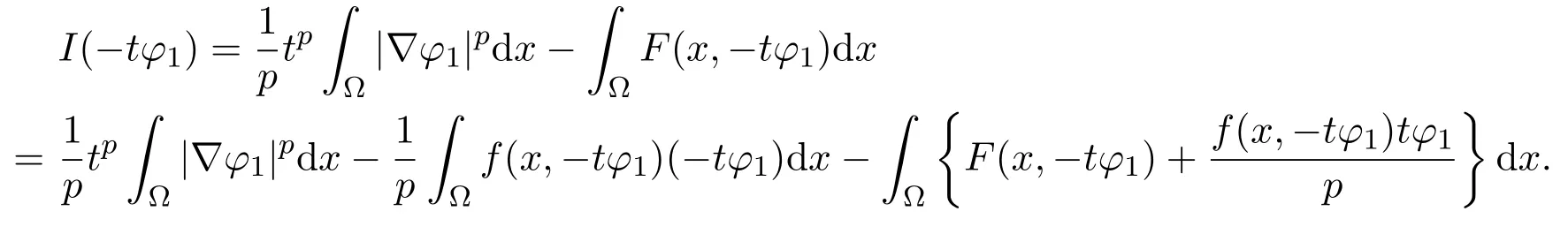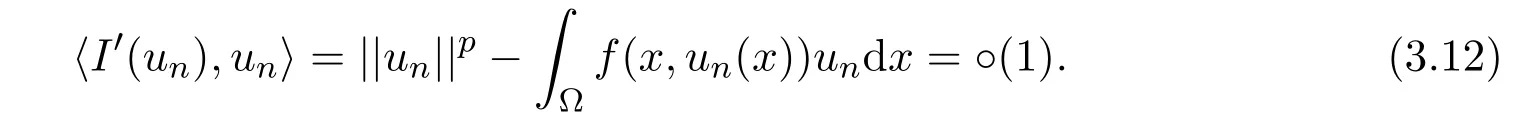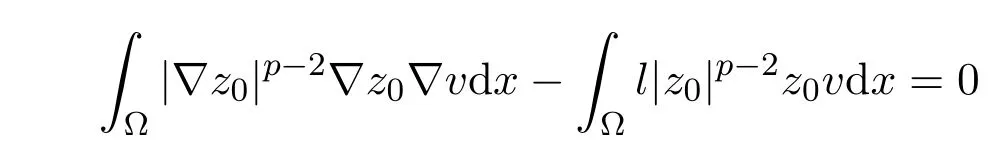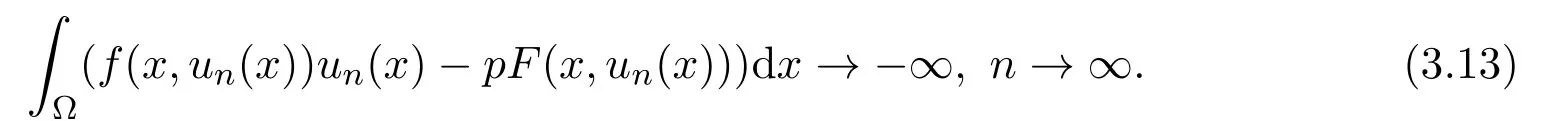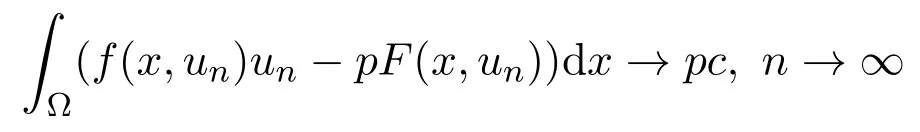非对称p-Laplacian Dirichlet问题的非平凡解
2014-07-18胡玉玲裴瑞昌
胡玉玲,裴瑞昌
(天水师范学院数学与统计科学学院,甘肃天水741001)
非对称p-Laplacian Dirichlet问题的非平凡解
胡玉玲,裴瑞昌
(天水师范学院数学与统计科学学院,甘肃天水741001)
研究了一类非对称的p-Laplacian(p>1)Dirichlet问题.在正半轴不需要假设Ambrosetti-Rabinowitz的超二次条件下,利用山路定理建立非平凡解的存在性结果.
山路理论;渐近线性;超线性;Dirichlet问题;单侧共振
1 引言
考虑下述p-Laplacian(p>1)Dirichlet问题:

(H1)存在q∈(p,p∗)及A,B>0,使得成立,其中
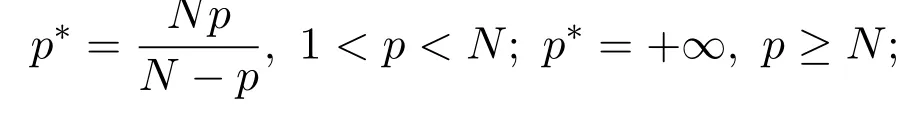
(H2)
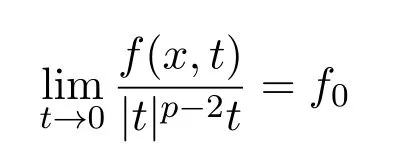
对a.e.x∈Ω一致成立,这里f0∈[0,+∞);
(H3)
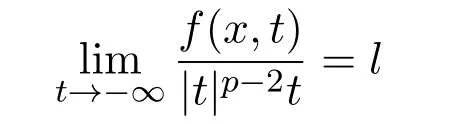
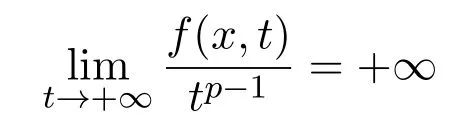
众所周知,问题(1.1)的非平凡解等价于C1-能量泛函:
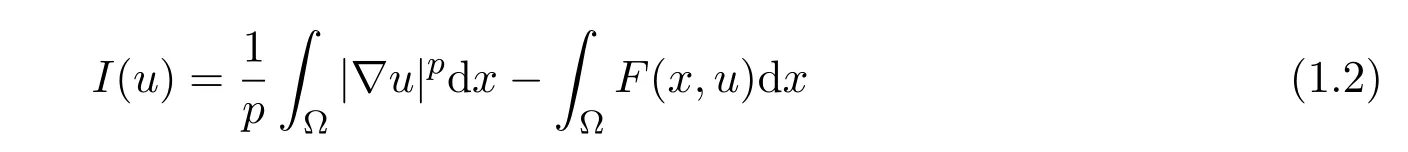
的非零临界点.寻求泛函I的临界点的主要工具是山路理论[15].应用这个理论于(1.2)式中的泛函I,通常不得不假设另一个技巧条件[1],那就是,对某个θ>0及M>0,

条件(AR)在验证泛函I有山路几何结构和(PS)c序列有界的过程中起着非常重要的作用.
通过简单的计算,易知条件(AR)推出:
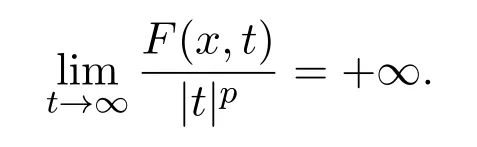
那就是,f(x,t)关于|t|p−2t在无穷远处是超线性的.
易知在条件(H3)和(H4)下,Ambrosetti-Rabinowitz-型条件(AR)不再成立.近年来, Costa和Magalh˜aes[67]运用下述条件代替条件(AR)考虑了问题(1.1):
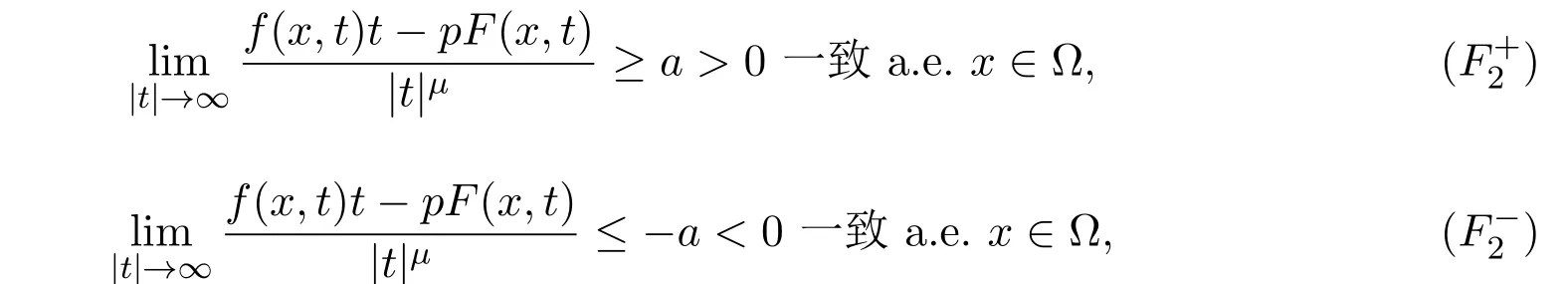
及
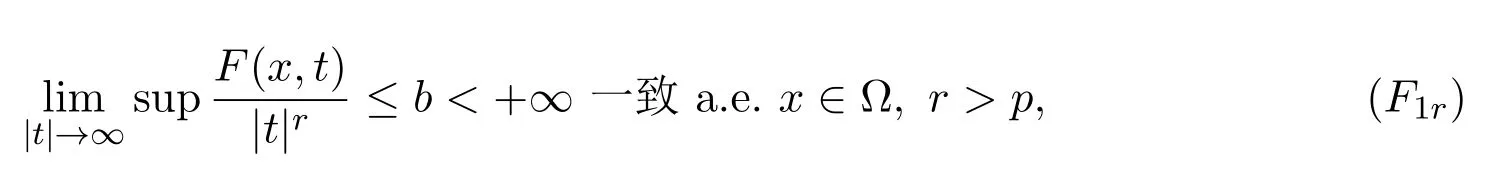
其中


及
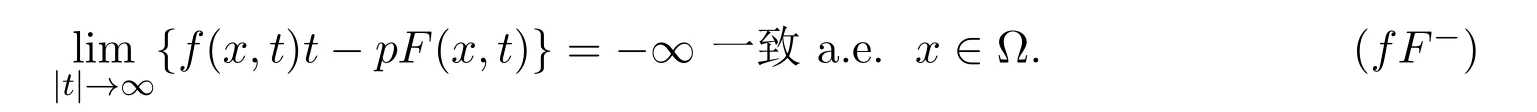
于是,文献[8]提出这样一个问题:如果不再成立,问题(1.1)仍然有一个非平凡解?通过考虑渐近线性问题,在文献[8-9]中给出肯定的回答.那就是:非线性项f(x,t)注意到在正无穷远处是渐近线性的.关于f(x,t),也给出两个例子:一个满足他们的条件(f1)-(f3),但不满足另一个满足所有条件(f1)-(f3)和事实上,就这个问题自身而言,如果人们想用山路理论寻求泛函I的临界点,在验证泛函I满足(PS)条件时,会遇到一定的困难,但是,他们巧妙利用一个变形后的山路理论来克服它.关于f(x,t),通过介绍其他的条件,一些存在性结果也被获得,见文献[10-12].
自然会问:当非线性项f(x,t)在正无穷远处是超线性的而在负无穷远处是渐近线性情形,像条件(H3)和(H4),泛函I有没有非平凡的临界点?特别地,当非线性项f(x,t)在负无穷远处发生共振而在正无穷远处是超线性情形,泛函I有没有非平凡的临界点?这些问题是很有趣的,就目前为止,这些问题很少被别人考虑.由于它们既不是超线性问题也不是渐近线性问题,我们定义它们为混合线性问题.本文的主要目标是运用山路理论及变形后的山路理论[10]肯定回答上述问题.
2 主要结果及引理
让λ1是的第一特征值,是λ1的特征函数.上的范数,用上的范数.相应地,

定理2.1假设(H1)-(H4)成立,且f0<λ1 附注2.2鉴于条件(H3)和(H4),问题(1.1)被称作混合线性问题.所以,定理2.1是完全不同于文献[8-9,13-14]中所得到的结果. 定理2.3假设t→−∞则问题(1.1)至少有一个非平凡解. 附注2.4当l=λ1,问题(1.1)被称作负无穷远处共振.这种情形是新的,完全不同于文献[15-16]的结果.在此,给出一个关于非线性项f(x,t)的例子,它满足条件(H1)-(H4):定义 这里g(t)∈C(R),g(0)=0;g(t)≥0,t∈R.此外,存在t0>0使得g(t)≡λ1,|t|≥t0. 命题2.5(文献[10],定理1)让E是实的Banach空间,假设I∈C1(E,R)满足 其中α<β,ρ>0及u1∈E,且||u1||>ρ.让c≥β被定义为: 这里Γ={γ∈C([0,1],E),γ(0)=0,γ(1)=u1}是连接0和u1的所有道路的集合.则,存在一个序列{un}⊂E,使得 引理2.6让φ1>0是λ1的特征函数,∥φ1∥=1及(H1)-(H4)成立,如果f0<λ1.则: (ii)如果l∈(λ1,+∞),则I(tφ1)→−∞,t→+∞. 证明由条件(H1)-(H4),若l∈(λ1,+∞),则对任意ε>0,存在A1=A1(ε),B1=B1(ε)使得对所有(x,s)∈Ω×R及对某个q∈(p,p∗),N>p;对某个q∈(p,+∞),1≤N≤p, 选择ε>0,使得(f0+ε)<λ1.运用(2.1)式,Poincar´e不等式及Sobolev不等式:|u|qq≤K||u||q,有 于是,如果选择||u||=ρ>0足够小,(i)被证明. 另一方面,如果l∈(λ1,+∞),选择ε>0使得l−ε>λ1并运用(2.2),有 这样(ii)已被证明. 定理2.1的证明根据引理2.6,山路理论的几何条件成立.于是,只要验证(PS)条件[3]成立.让是一个(PS)序列使得对每个n∈N, 其中c(c>0)是一个正的常数,{εn}⊂R+是一个收敛于零的序列.根据标准证法,为了证明{un}有一个收敛子列,不得不证明它是一个有界序列.为了证明其成立,使用反证法.假设存在一个子列{un},有||un||→+∞,n→∞.不失一般性地,可假设成立,定义显然,||zn||=1,∀n∈N,则可以抽取一个子列(记为{zn}),使得 在上式中取极限,结合(3.3)式,有 现在,证明z0(x)≤0对a.e.x∈Ω成立.在(3.7)式中选取v=z+0=max{z0,0},有 定理2.3的证明由于l=λ1,显然,引理2.6的(i)成立.我们只要验证引理2.6的(ii)成立.让u=−tφ1,则 很明显,由(3.11)式推出: 一致于x∈Ω,推出 另一方面,由(3.12)式推出pI(un)− 与(3.13)式相矛盾.因此,{un}有界. [1]Ambrosetti A,Rabinowitz P H.Dual variational methods in critical point theory and applications[J].J. Funct.Anal.,1973,14:349-381. [2]Brezis H,Nirenberg L.Positive solutions of nonlinear elliptic equation involving critical Sobolev exponents[J]. Comm.Pure Appl.Math.,1983,36:437-477. [3]Rabinowitz P H.Minimax Methods in Critical Point Theory with Applications to Di ff erential Equations: CBMS Regional Conference Series in Math,No.65[C].Rhode Island:American Mathematical society,1986. [4]Li G B.Nontrivial solutions of quasilinear elliptic equations in W1,p0(Ω)involving limiting nonlinearities[J]. Acta.Math.Sci.,1987,7:329-339. [5]Shen Y T.The nontrivial solutions of quasilinear elliptic equations in W1,p0(Ω)[J].Sci.Sinica,Ser.A, 1984,27(7):720-730. [6]Costa D G,Magalh˜aes C A.Variational elliptic problems which are nonquadratic at in fi nity[J].Nonlinear Anal.TMA,1994,23:1401-1412. [7]Costa D G,Magalh˜aes C A.Existence results for perturbations of the p-Laplacian[J].Nonlinear Anal.TMA, 1995,24:409-418. [8]Li G B,Zhou H S.Asymptotically linear Dirichlet problem for the p-Laplacian[J].Nonlinear Anal.TMA, 2001,43:1043-1055. [9]Zhou H S.Existence of asymptotically linear Dirichlet problem[J].Nonlinear Anal.TMA,2001,44:909-918. [10]Costa D G,Miyagaki O H.Nontrivial solutions for perturbations of the p-Laplacian on unbounded domains[J].J.Math.Anal.Appl.,1995,193:737-755. [11]Anane A,Gossez J P.Strongly nonlinear elliptic problems near resonance[J].Comm.PDE,1990,15:1141-1159. [12]Schechter M.Superlinear elliptic boundary value problems[J].Manuscripta Math.,1995,86:253-265. [13]Liu S B.Multiple solutions for coercive p-Laplacian equations[J].J.Math.Anal.Appl.,2006,316:229-236. [14]Huang Y S,Zhou H S.Positive solution for−△pu=f(x,u)with f(x,u)growing as up−1at in fi nity[J]. Appl.Math.Lett.,2004,17(8):881-887. [15]Liu J Q,Su J B.Remarks on multiple nontrivial solutions for quasilinear resonant problems[J].J.Math. Anal.Appl.,2001,258:209-222. [16]Jiu Q S,Su J B.Existence and multiplicity results for Dirichlet problem with p-Laplacian[J].J.Math. Anal.Appl.,2003,281:587-601. [17]V´azquez J L.A strong maximum principle for some quasilinear elliptic equations[J].Appl.Math.Optim., 1984,12:191-202. Nontrivial solutions for asymmetric p-Laplacian Dirichlet problem Hu Yuling,Pei Ruichang (College of Mathematical and Statistical Science,Tianshui Normal University,Tianshui741001,China) A class of asymmetric p-Laplacian Dirichlet problem is studied.Without Ambrosetti-Rabinowitz′s super quadratic condition on the positive semiaxis,the existence of nontrivial solutions is established by using mountain pass theorem. mountain pass theorem,asymptotically linear,superlinear,Dirichlet problem,one side resonance O175.23 A 1008-5513(2014)01-0077-07 10.3969/j.issn.1008-5513.2014.01.012 2013-12-25. 国家自然科学基金(11101319). 胡玉玲(1974-),助教,研究方向:偏微分方程. 2010 MSC:35J35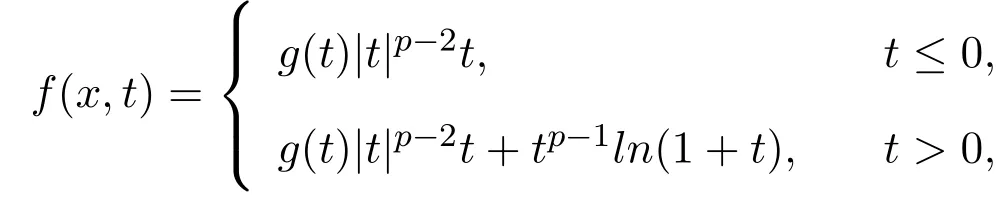
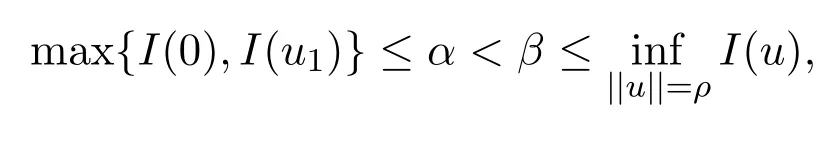
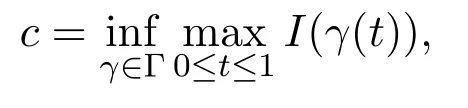
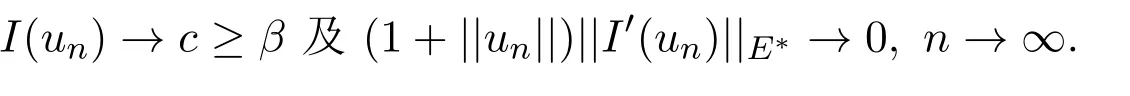
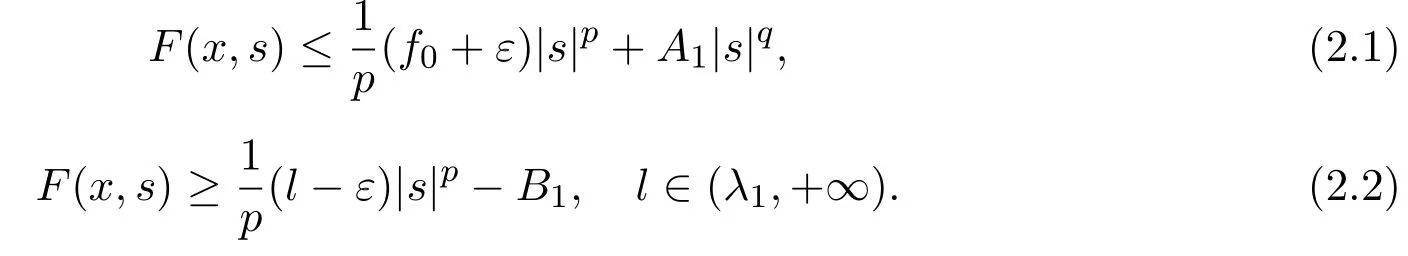
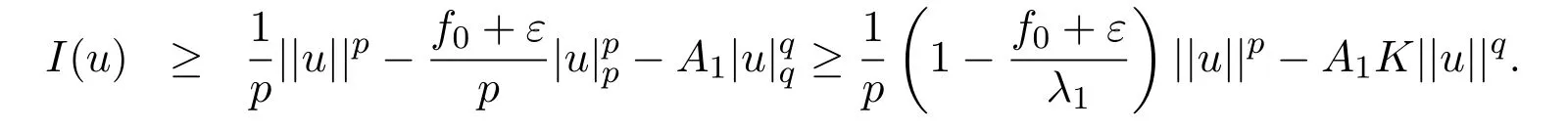

3 定理的证明