同心球间流动三模类Lorenz系统的动力学行为及数值仿真

王贺元,高焱

(1.辽宁工业大学理学院,辽宁锦州121001;2.辽宁石化职业技术学院,辽宁锦州121001)

同心球间流动三模类Lorenz系统的动力学行为及数值仿真

王贺元1,高焱2

(1.辽宁工业大学理学院,辽宁锦州121001;2.辽宁石化职业技术学院,辽宁锦州121001)

讨论了同心球间旋转流动的类Lorenz型方程组的动力学行为及其数值模拟问题,求出了该方程组平衡点,并对其稳定性进行了分析,证明了该方程组吸引子的存在性,对类Lorenz方程组的动力学行为进行了数值模拟,数值试验表明此类Lorenz型方程组存在极限环和奇怪吸引子.

Navier-Stokes方程;球Couette流;Lorenz系统

1 引言

两个同心旋转球之间的流动简称为球Couette流动,作为一个简单的模型,研究它能够为揭示流动失稳转捩至湍流这一重大理论课题的规律提供线索.由于球Couette流动更象全球大气流动,研究它也能成为研究大气物理提供一个粗略的模型,并提供一些理论指导.因此,球Couette流动的研究有很大的理论价值,长期以来它一直是人们普遍关注的热点问题,相关文献非常丰富[1-7].文献[2-3]通过实验发现,在低Reynolds数下的球Couette流是轴对称和关于赤道反射对称的,当内外球之间的间隙η介于(0.12,0.24)时(这里的间隙是指：通过无量纲化而使内球半径化为1后,内外球之间的距离),球Couette流在子午面上存在三种形式,即0-涡,1-涡和2-涡.文献[4-5]利用拟谱方法和配置法验证了前面的实验结果.文献[6]的实验首次验证了球Couette并不是η和Reynolds的唯一函数,流动的最终的平衡状态还依赖于流动的过去状态,特别是在趋向最终状态时的内球加速度.文献[2-3,6]中发现存在一个临界Reynolds数Rec,当Re≥Rec时才会出现Taylor涡,文献[7]进一步利用各种方法,如具有差分,拟谱或配置法的弧长连续算法分别得到:当η=0.18时,Rec1=645±0.05, Rec2=740±0.05,即当ReRec时,出现2-Taylor涡,如图1所示.综上可以看出,对两同心旋转球间流动的研究一直还停留在实验和数值模拟上,由于该问题虽是轴对称的,但它毕竟还是一个三维问题,而且在球坐标系下的Navier-Stokes方程非常复杂,所以理论上探讨同心旋转球间流动的Navier-Stokes方程解的存在,唯一及正则性等问题极为困难.

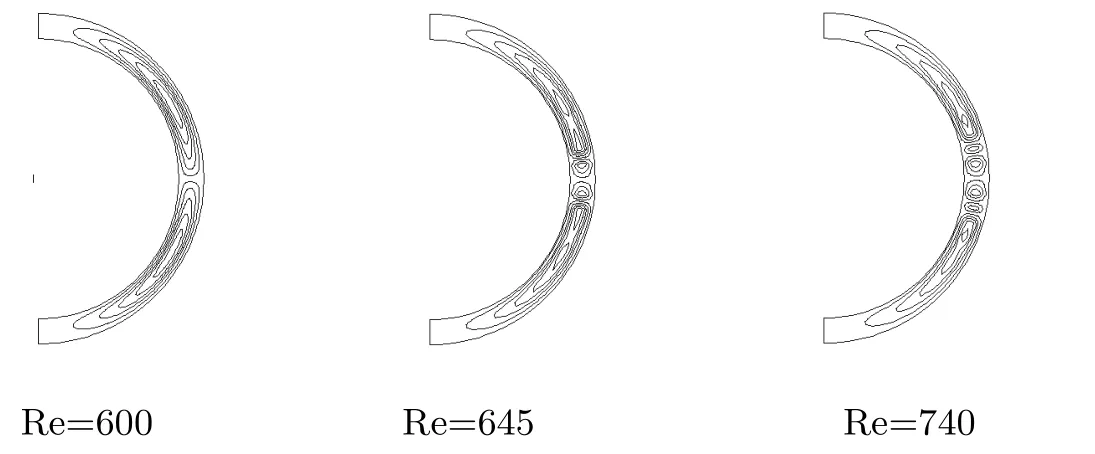
图1 Couette流

文献[1]对同心旋转球间流动的Navier-Stokes方程谱展开后进行三模态截断,得到一个类似于Lorenz系统[8-9]的类Lorenz方程组,讨论了这个类Lorenz方程组的静态分叉问题,给出其奇异点存在的条件,并计算出了解分支.本文选取不同的截断模式,获得一个新三模类Lorenz方程组,给出该方程组平衡点及其稳定性的讨论,证明了该方程组吸引子的存在性,数值模拟了雷诺数在一定范围内变化时类Lorenz方程组的动力学行为.

2 三模类Lorenz型方程组的平衡点及其稳定性分析

为获得流体系统的动力学行为,对其进行低模分析是非常有意义的.作为较早发现的混沌模型Lorenz系统只包含三个模态,但它的形式简单,内容丰富,不仅开辟了数学上一些振奋人心的新领域,而且还与湍流现象密切相关.由于它是非线性的,纯粹分析还是困难的,许多结果是通过数值分析在计算机上算出来的.对两球间的旋转流动,也存在类似于Lorenz方程组的典型方程组,即在谱展开式中,取少数几个主要模式(基函数),得到一个类Lorenz型方程组,进而讨论其平衡点的稳定性、吸引子的存在性、分歧、混沌等非线性现象.本文选取如下截断模式:

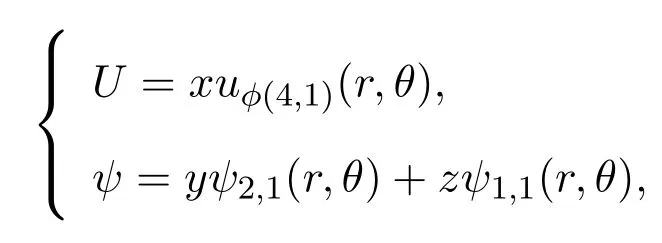
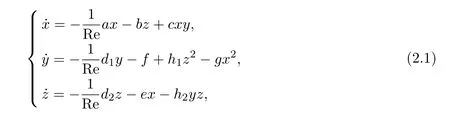
其中a,b,c,d1,d2,e,f,h1,h2,g为谱展开系数,均为正常数.这样做的意义在于:不但克服了谱方法得到的庞大的常微分方程组性质不好把握的困难,而且得到的类Lorenz型方程组包含了非常丰富而有意义的内容,这对探讨Navier-Stokes方程的分歧、湍流等非线性现象非常重要.由于采用Stokes算子的特征函数作为逼近子空间的基函数,因此截断法具有明显的物理意义:每一个基函数都可以看成是一种基本的流动模式,实际的流动则可以看成是这些基本流动模式的迭加.

微分方程组(2.1)的平衡点应满足如下的代数方程组:

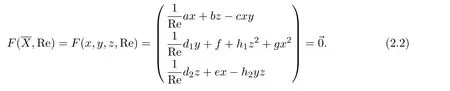
方程组(2.2)有三个解,

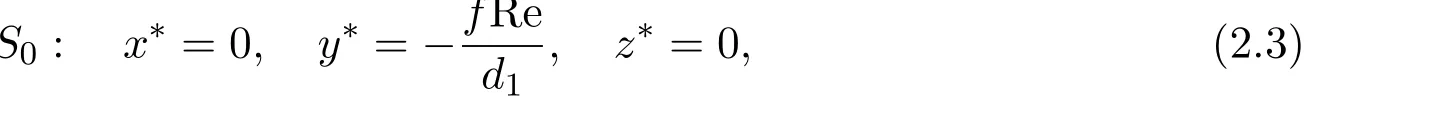
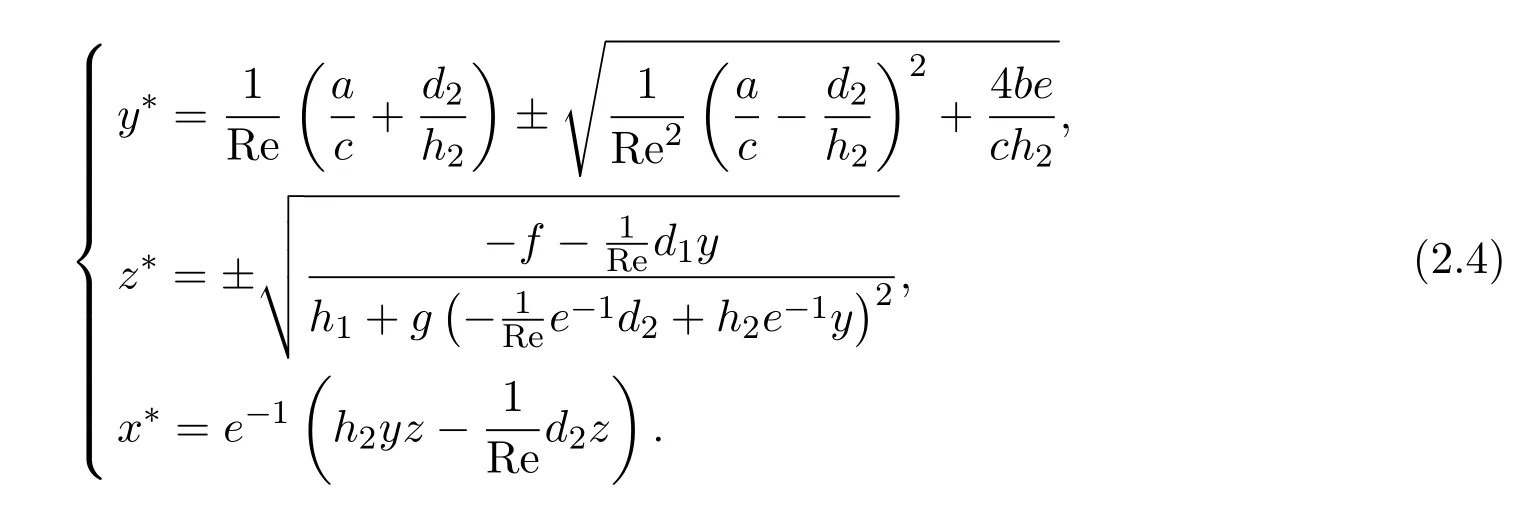
它们就是类Lorenz型方程组(2.1)的平衡点,这里Re1,Re2是方程的解, Re1≈3300,Re2≈608700.平衡点(2.3)代表了球Couette流的基本流,平衡点(2.4)式代表了球Couette流的另一种非基本流的流动状态.把方程组(2.1)在平衡点附近线性化,经计算得

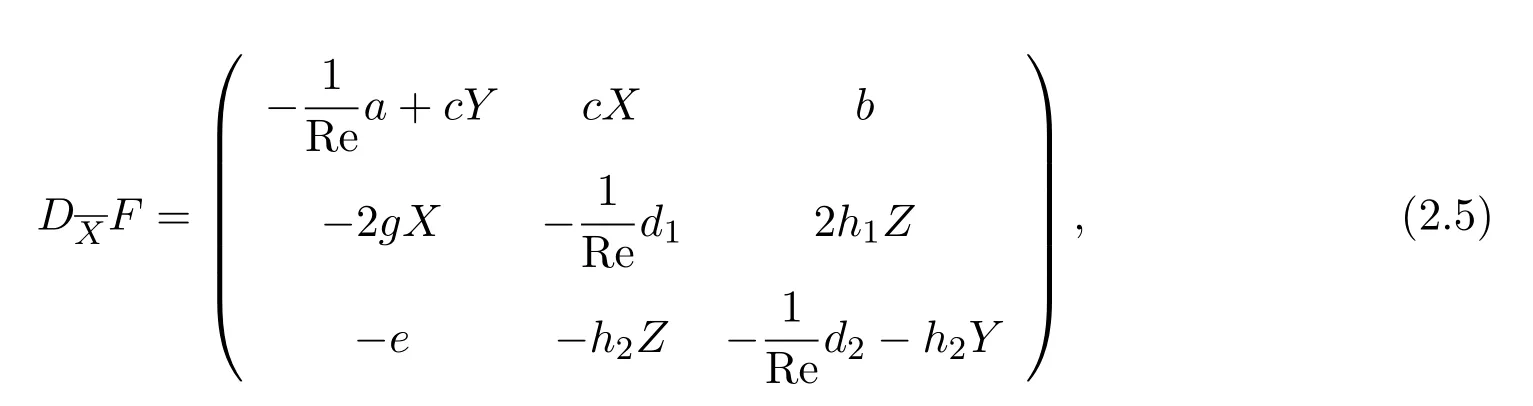
其中(X,Y,Z)分别为平衡点的三个分量.

下面讨论平衡点S0,S±的稳定性,将平衡点S0的三个分量(X,Y,Z)代入(2.5)式,则得

到矩阵(2.5)的特征方程:

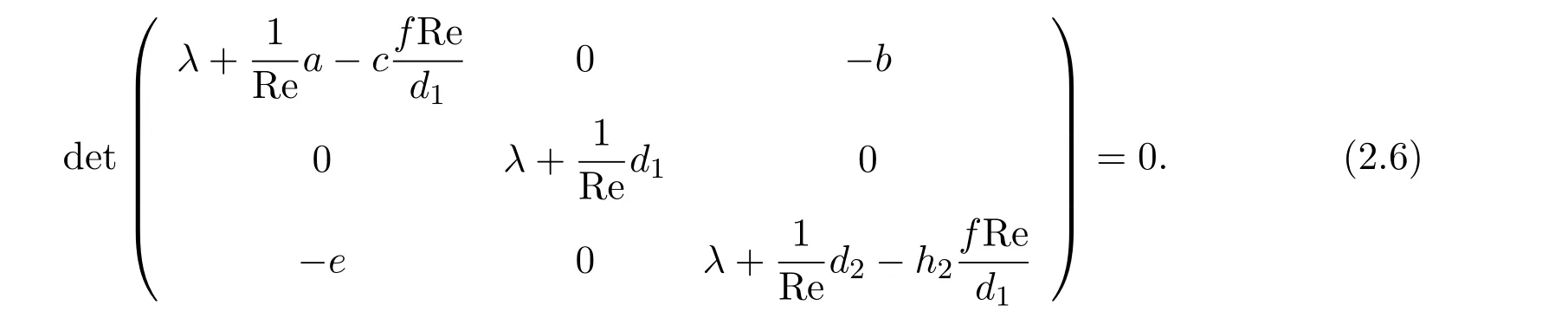
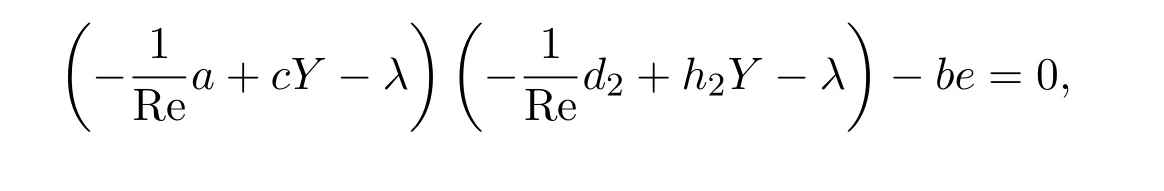
即

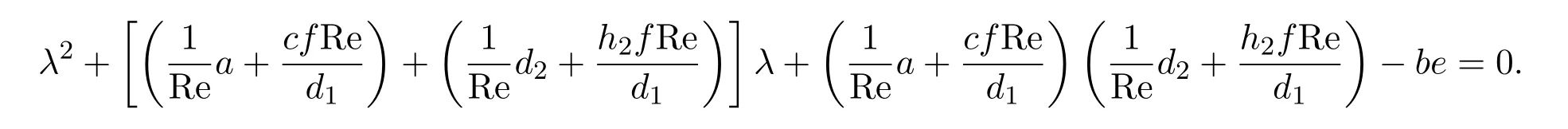
设Re3,Re4为

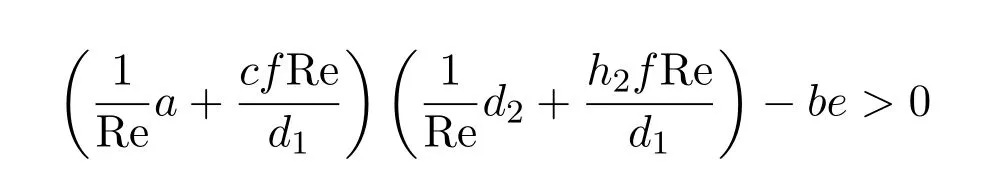
的解,且Re3Re4时,方程有两个负实部的根,此时S0稳定.

对S±,将平衡点S±的各个分量(X,Y,Z)代入矩阵(2.5),与前面的做法相同,通过计算发现,∀Re>0所有特征值均为负实部,因此,平衡点S±稳定.

3 吸引子的存在性

为了讨论类Lorenz型方程组(2.1)的动力学行为,把它改写成如下形式:

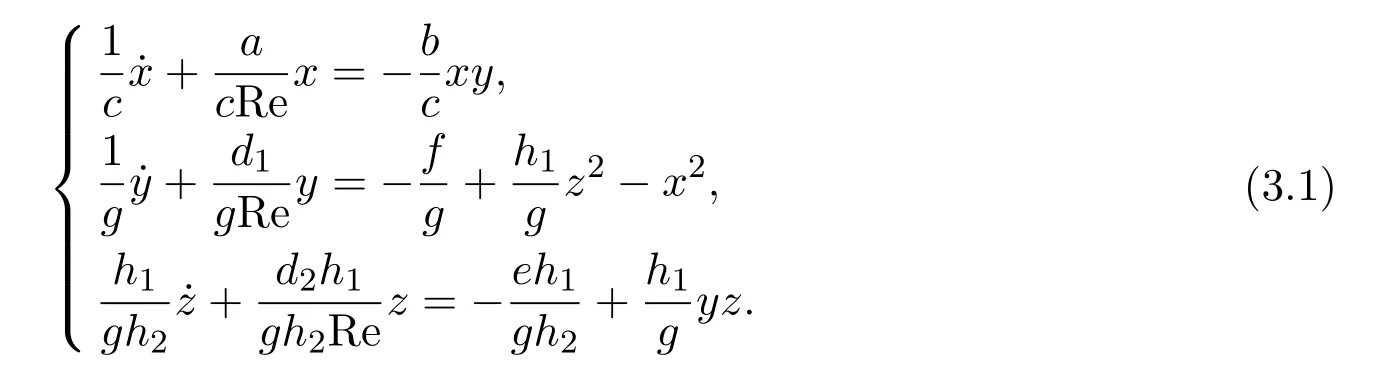
在以上三个方程两边分别乘以x,y,z相加后得:

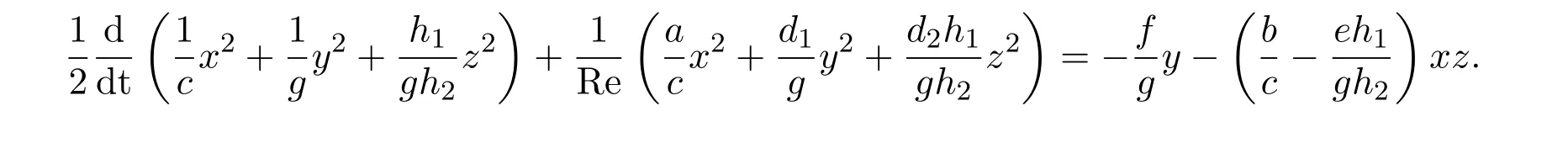
利用Young不等式得,

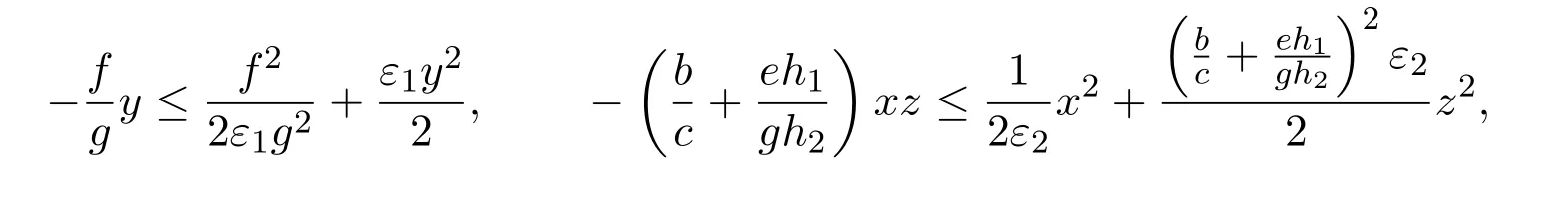
所以,

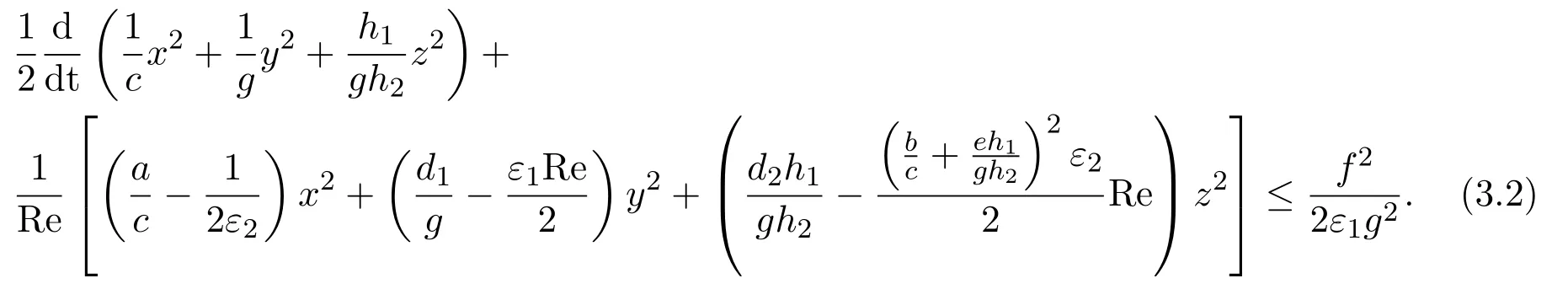
由于正常数ε1,ε2可任意选取,故可以选到正数M0,M1,M2,满足

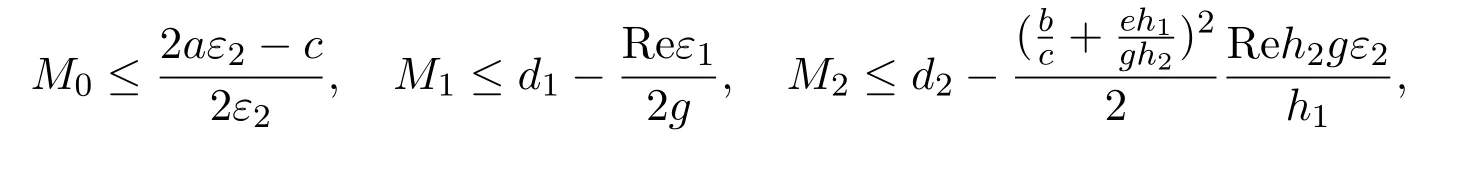
即

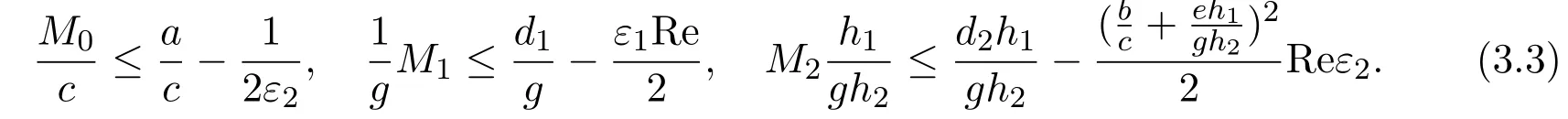
再取M=min{M0,M1,M2},于是

令

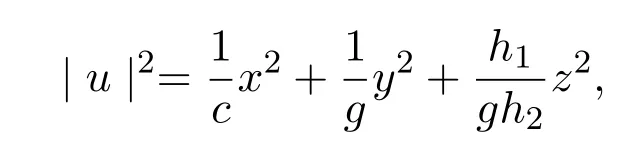
不难验证,|u|是一个范数,于是从(3.2)-(3.4)式得到:

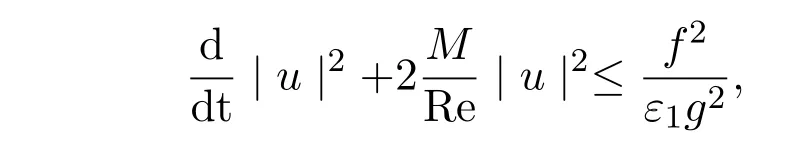
运用Gronwall不等式[11],有

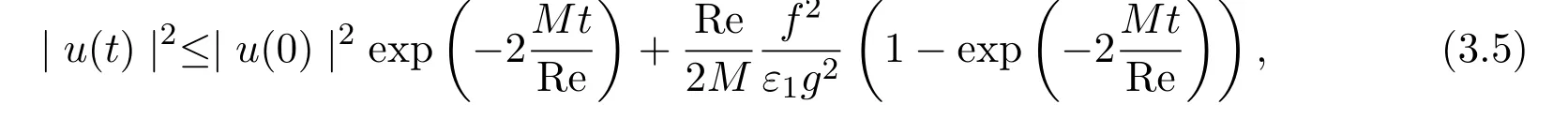
故

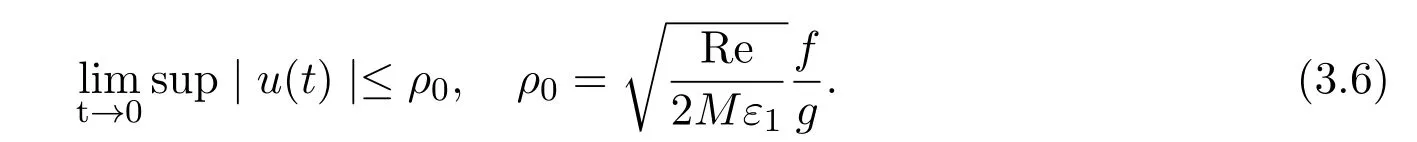
不等式(3.5)说明,若记B(0,ρ)为H(H一般是Hilbert空间,这里就是普通的三维欧氏空间)中以0为中心,以ρ≥ρ0为半径的球,则B(0,ρ)是方程组(2.1)的初值问题所确定的算子半群S(t)的一个不变集,即若u0∈B(0,ρ),

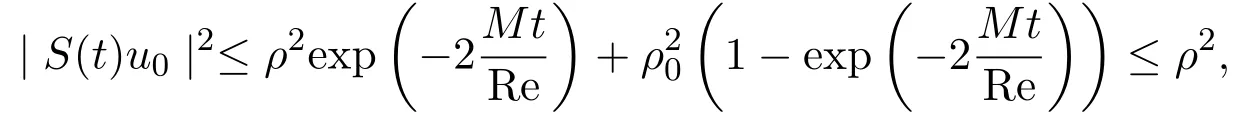
故S(t)B(0,ρ)⊂B(0,ρ).并且当ρ>ρ0时,这些球是吸收集,实际上,任一有界集D,都有

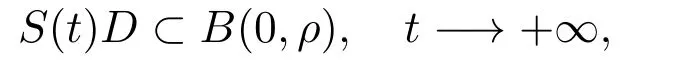
故方程组(2.1)存在吸引子[10-11].

4 数值模拟

下面对类Lorenz型方程组(2.1)的动力学行为进行数值模拟,通过计算得方程组(2.1)的系数如下:

a=309.681,b=3.21,c=1.346,d1=1218.503,d2=1208.771,e=2.744,

h1=1.696,h2=3.305,f=0.11g=1.057.

随着雷诺数Re的增大,类Lorenz方程组(2.1)的平衡点稳定性发生了变化,出现了Hopf分岔和混沌等非线性现象.下面数值模拟系统(2.1)的动力学行为.

1)通过数值计算得方程组(2.1)在Re<7513.95···时,平衡点S0稳定,解轨线为螺旋线趋于平衡点S0,见图2.

2)当Re≥7513.95···平衡点S0开始不稳定,围绕平衡点S0出现奇怪吸引子,如图3,图4.

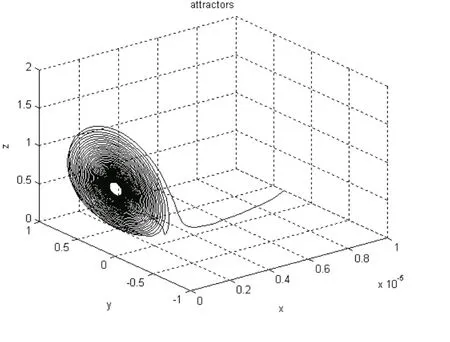
图2 Re=164.58

图3 Re=194.43

3)当Re进一步增大时,有一对特征值实部接近于0,即出现一对纯虚特征值,系统(2.1)发生了Hopf分岔.解轨线为单闭轨线,即出现极限环,如图5.

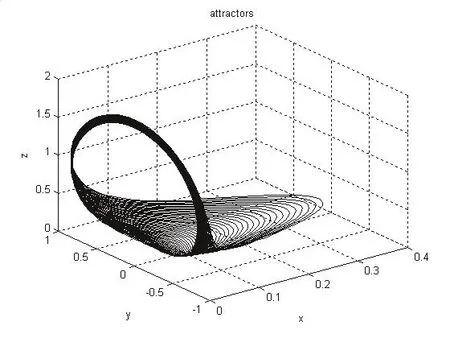
图4 Re=7835.76

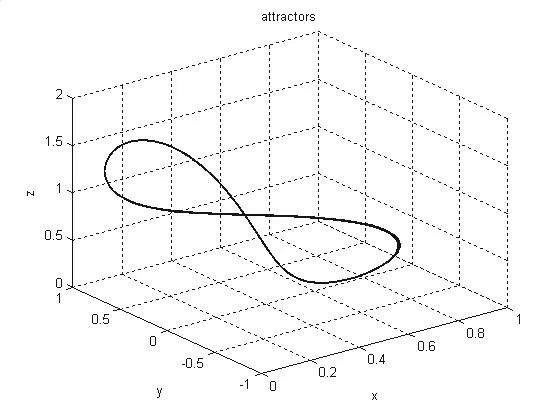
图5 Re=8132.69

参考文献

[1]王贺元,蒋海斌.两同心球间旋转流动类Lorenz方程组的分歧分析[J].高等学校计算数学学报,2007,29(3): 278-288.

[2]Khlebutin G N.Stability fl uid motion between a rotating and a stationary concentric spheres[J].Fluid Dyn., 1986,3:31-34.

[3]Sawatzki O,Zierep J.Das stromfeld in spalt Zwischen Zwei Konzentrischen Kugel fl aechen,von Denen die innore rotiert[J].Acta.Mechanica,1970,9:13-35.

[4]Marcus P S,Tuckerman L S.Simulation of fl ow between two concentric rotating spheres[J].Part 1.Steady States,J.Fluid Mech.,1987,185:1-30.

[5]Marcus P S,Tuckerman L S.Simulation of fl ow between two concentric rotating spheres[J].Part 2.Transitions,J.Fluid Mech.,1987,185:31-66.

[6]Wimmer M.Experiments on a viscous fl uid fl ow between two concentric rotating spheres[J].J.Fluid Mech., 1976,73:371-335.

[7]Schrauf G.Branching of Navier-Stokes Equations in a Spherical Gap[A].In Proc.8th Intl.Conf.Numerical Methods in Fluid Dyn.,Aachen:Springer,1983.

[8]Lorenz E N.Deterministic nonperiodic fl ow[J].J.Atoms.Sci.,1963,20:130-135.

[9]Swinney H L,Gollub J P.Hydrodynamic Instabilities and the Transition to Turbulence[M].New York: Springer-Verlag,1981.

[10]Hilborn R C.Chaos and Nonlinear Dynamics[M].Oxford:Univ.Press,1994.

[11]李开泰,马逸尘.数理方程Hilbert空间方法(下)[M].西安:西安交通大学出版社,1992.

The dynamical behavior and the numerical simulation of the Lorenz system of the fl ow between two concentric rotating spheres

Wang Heyuan1,Gao Yan2
(1.School of Sciences,Liaoning University of Technology,Jinzhou121001,China; 2.Department of computer science,Liaoning Petro-Chemical Vocational Technology College, Jinzhou121001,China)

In order to study the problem of rotating fl ow we investigate the dynamical behavior and the numerical simulation of the model system similar to the Lorenz equations of the Navier-Stokes equations for the fl ow between two concentric rotating spheres.Its stationary points and the stability are presented,the existence of attractor is proved.Chaos behavior is simulated numerically by computer with the changing of Reynolds number,Numerical experiments show that the existence of limit cycles and strange attractors.

Navier-Stokes equations,spherical Couette fl ow,the Lorenz system

O357.1;O241.82

A

1008-5513(2014)01-0007-07

10.3969/j.issn.1008-5513.2014.01.002

2013-09-20.

辽宁省教育厅科研基金(L2013248);锦州市科技专项基金(13A1D32).

王贺元(1963-),博士,教授,研究方向：非线性系统分歧混沌理论及其数值分析.

2010 MSC:65J15,47H15,65M60