Schur 定理的推广

姚裕丰

(上海海事大学数学系,上海201306)

Schur 定理的推广

姚裕丰

(上海海事大学数学系,上海201306)

通过计算及归纳的方法,得到了n×n矩阵代数中极大线性无关的反交换2-幂零矩阵的个数,推广了相关文献中的一般线性李代数gl(n)的交换子代数的最大维数这一结论.

反交换矩阵对;2-幂零矩阵;线性无关

1 引言及主要结果

1905年,文献[1]证明了n×n复矩阵代数中极大线性无关的交换矩阵的个数是这里[c]表示不超过c的最大整数,此结论称为Schur定理.之后,文献[2-3]给出了Schur定理更为简洁的证明,并且把基域推广到任意的域(不一定是特征零，也不一定代数闭).文献[4-5]中给出了一些特殊的李代数中极大交换子代数的维数.文献[6]确定了一般线性李超代数gl(1,n)的不可分解的交换子代数的最大维数.本文推广了Schur定理,得到如下主要结果:

定理1.1设F是一个域,Mn×n(F)是F上的n×n矩阵代数.则Mn×n(F)中极大线性无关的反交换2-幂零矩阵的个数是

2 预备知识

本文总假设F是一个域,V是F上n维向量空间.记Mn×n(F)为F上n×n矩阵代数,Un×n(F)为F上严格上三角n×n矩阵全体,EndF(V)为V上全体F-线性变换.众所周知,若取定V的一组基,则可将Mn×n(F)与EndF(V)等同起来.对于1≤i≤n,1≤j≤n,令eij为一n×n矩阵,它的第i行第j列为1,其余位置均为0.对于任一有理数c,用[c]表示不超过c的最大整数.

定义2.1(1)矩阵A∈Mn×n(F)(线性变换A∈EndF(V))可以称之为幂零矩阵(线性变换),如果存在充分大的自然数m使得Am=0(Am=0).

(2)矩阵A∈Mn×n(F)(线性变换A∈EndF(V))可以称之为2-幂零矩阵(线性变换),如果A2=0(A2=0).

(3)矩阵A,B∈Mn×n(F)(线性变换A,B∈EndF(V))可以称之为互相反交换,如果AB=−BA(AB=−BA).

注记2.1矩阵A∈Mn×n(F)(线性变换A∈EndF(V))是幂零矩阵(线性变换)当且仅当An=0(An=0).

引理2.1设V是F上n维线性空间,S⊂EndF(V),且满足以下条件:

则存在非零v∈V使得Av=0,∀A∈S.

证明注意到EndF(V)是有限维,取S中一组极大线性无关组{A1,···,Al}.由于An1=0,

从而存在非零v1∈V使得A1v1=0.设

从而V1在A2的作用下不变.又An2=0,故存在非零v2∈V1使得A2v2=0.

一般地,

Vi:={w∈V|Ajw=0,∀1≤j≤i}̸=0,

且从而Vi在Ai+1的作用下不变.而=0,故

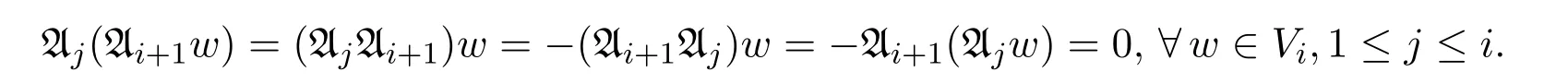
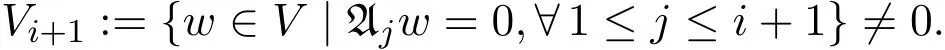
根据以上构造,取非零的v∈Vl,则Aiv=0,∀i=1,···,l.从而,Av=0,∀A∈S.

下面的结论是引理2.1的直接推论.

推论2.1设S⊂Mn×n(F),且满足以下条件:

则存在可逆的n×n矩阵P使得P−1SP⊂Un×n(F).

证明记Ξ为S生成的Mn×n(F)的子代数.由引理2.1知,不可约Ξ-模都是平凡的.考虑V作为Ξ-模的合成列: V=V(0)⊃V(1)⊃V(2)···⊃V(n−1)⊃V(n)=0.

则dimFV(i)=n−i,每个单因子Vi/Vi+1均为平凡的Ξ-模,0≤i≤n−1,从而存在V的一组基v1,···,vn使得

Av1=0,Avi+1∈spanF{v1,···,vi},∀A∈Ξ,1≤i≤n−1.

即存在可逆n×n矩阵P使得P−1SP⊂Un×n(F).

引理2.2设S⊂Mn×n(F),W是S生成的Mn×n(F)的子空间.则S中的矩阵为反交换的2-幂零矩阵当且仅当W中的矩阵为反交换的2-幂零矩阵.

证明充分性是显然的.下证必要性.

设S中的矩阵为反交换的2-幂零矩阵.取S中的一组极大线性无关组{A1,···,As}.对于任意的k1,···,ks,l1,···,ls∈F,

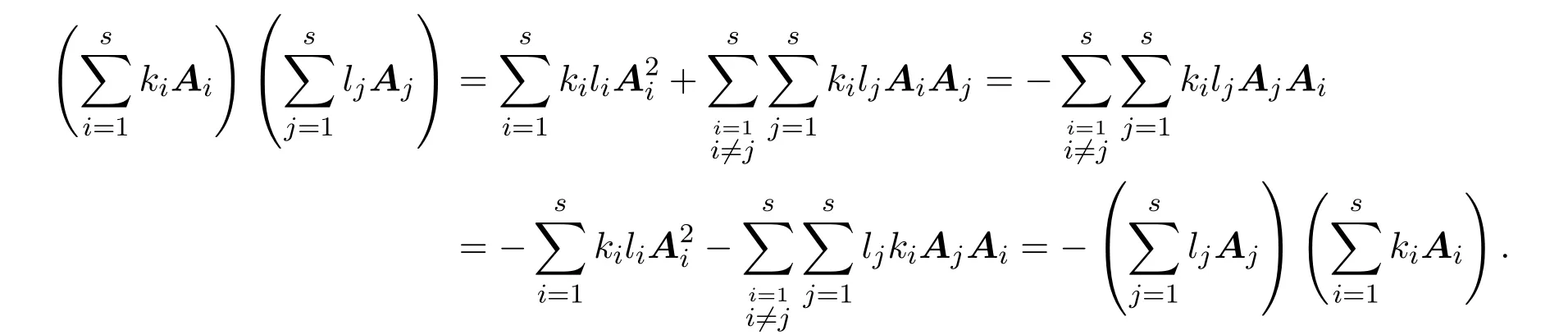
特别地,

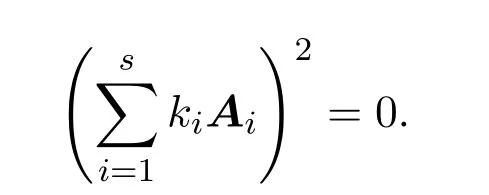
因此,W中的矩阵也为反交换的2-幂零矩阵.

3 定理的证明

对n用数学归纳法.n=1是平凡的情况.假设定理对(n−1)成立,接下来证明该定理对n也成立.用反证法.设S⊂Mn×n(F),且

AB=−BA,A2=B2=0,∀A,B∈S,且A̸=B.

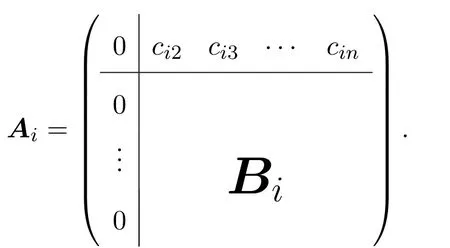
由于

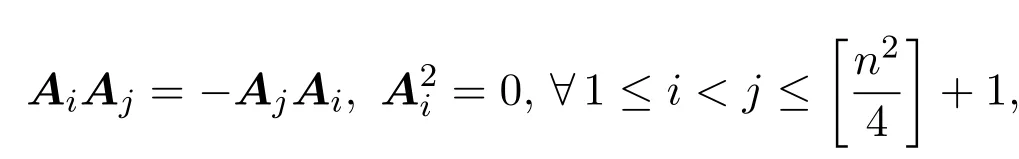
从而

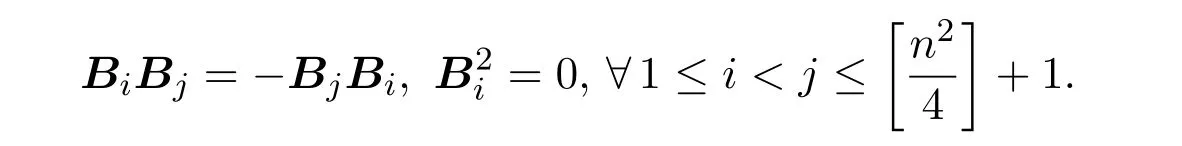
不失一般性,可设B1,···,Br线性无关.则对于任意满足的自然数i,存.令

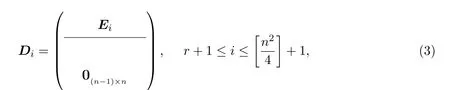
其中Ei是1×n矩阵,0(n−1)×n是(n−1)×n零矩阵.显然线性无关.

另一方面,由于P−1SP⊂Un×n(F),则存在(n−1)×(n−1)矩阵以及1×n矩阵使得

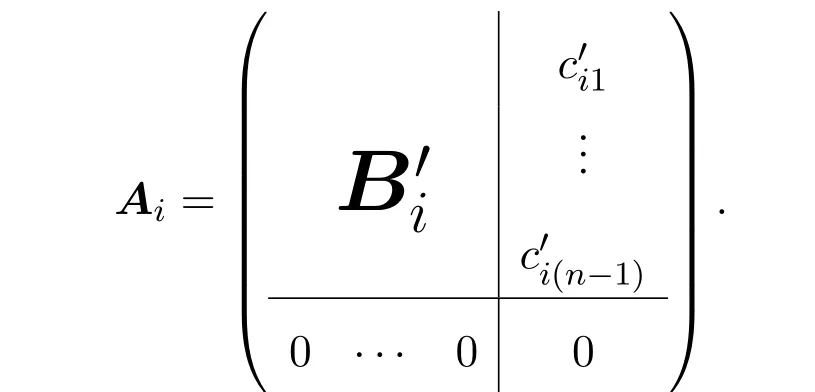
由于

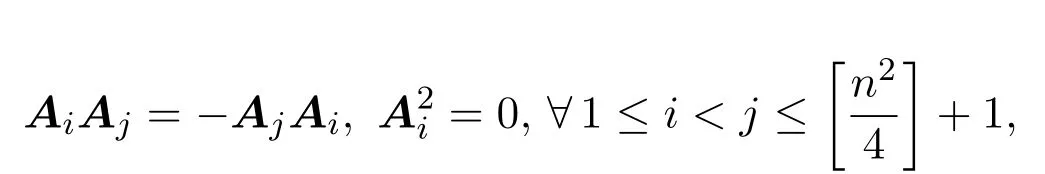
从而

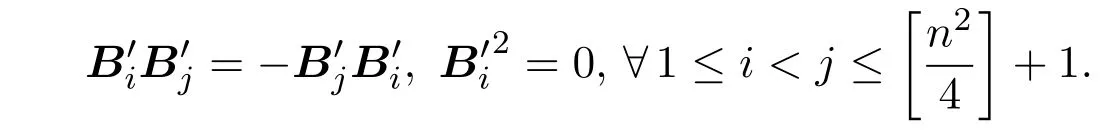
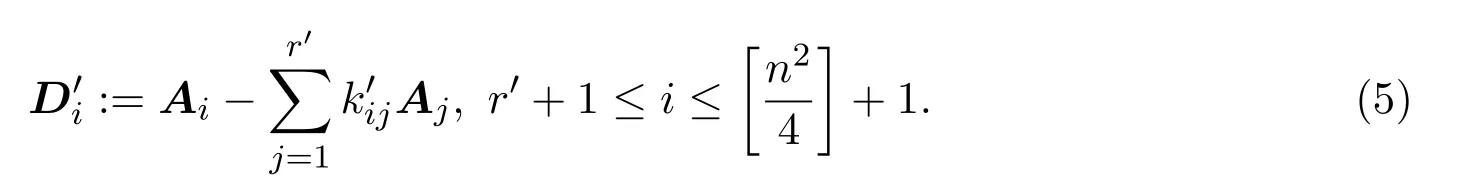
其中Fi是n×1矩阵,0n×(n−1)是n×(n−1)零矩阵.显然Fr′+1,···,线性无关.

由引理2.2以及(2),(3),(5),(6)式知,

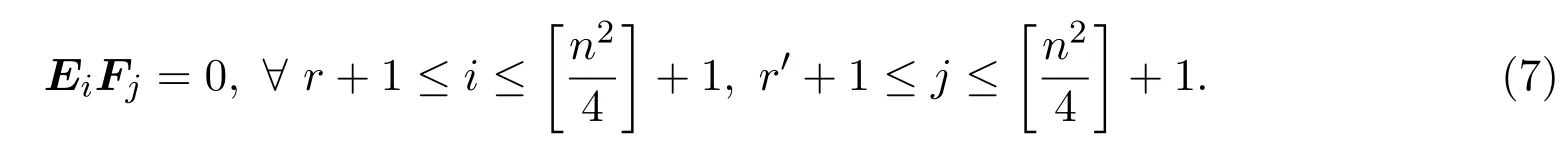
令

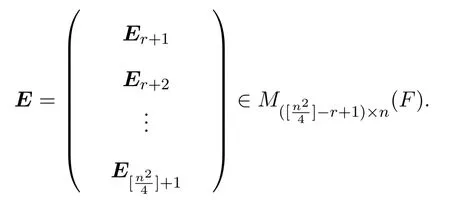
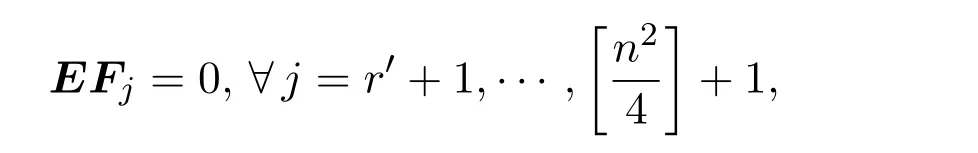
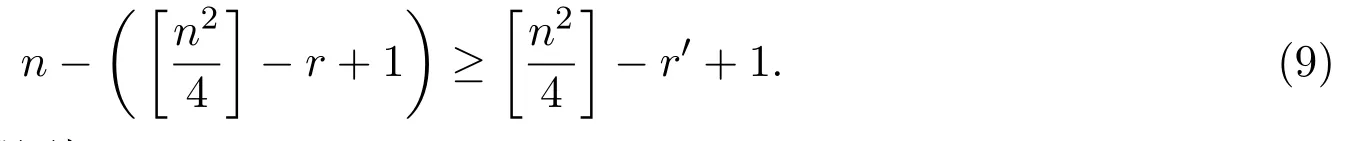
因此,根据(1),(4),(9)式得到:

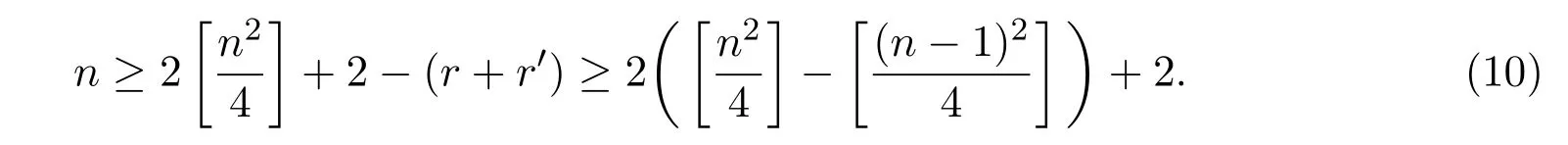
情形1n=2m是偶数.

此时,(10)式变为

2m≥2(m2−m(m−1))+2=2m+2,

矛盾.

情形2n=2m+1是奇数.

此时,(10)式变为

2m+1≥2(m(m+1)−m2)+2=2m+2,

矛盾.

以上矛盾表明Mn×n(F)中极大线性无关的反交换2-幂零矩阵的个数不超过注意到

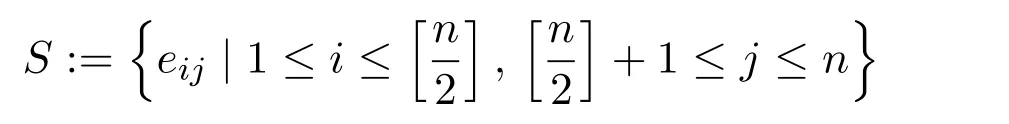
是Mn×n(F)中线性无关的反交换2-幂零矩阵族,且Card定理得证.

[1]Schur I.Zur theorie der vertauschbaren matrizen[J].J.Reine Angew.Math.,1905,130:66-76.

[2]Jacobson N.Schur′s theorems on commutative matrices[J].Bull.Amer.Math.Soc.,1944,50:431-436.

[3]Mirzakhani M.A simple proof of a theorem of Schur[J].Amer.Math.Monthly,1998,105:260-262.

[4]Burde D．On a re fi nement of Ado′s theorem[J]．Arch.Math.,1998,70:118-127．

[5]Burde D,Moens W．Minimal faithful representation of reductive Lie algebras[J]．Arch.Math.,2008,89: 513-523．

[6]王淑娟,刘文德．一般线性李超代数gl(1,n)的交换子代数的最大维数[J].黑龙江大学自然科学学报,2012, 29(4):452-454．

A generalization of Schur′s theorem

Yao Yufeng

(Department of Mathematics,Shanghai Maritime University,Shanghai201306,China)

With the aid of computation and induction,the maximal number of linearly independent anticommutative 2-nilpotent matrices of order n is obtained.This result generalizes result in the related literature, where the maximal dimension of commutative subalgebras in the general linear Lie algebra gl(n)was determined.

anti-commuting pairs of matrices,2-nilpotent matrices,linearly independent

O151.21

A

1008-5513(2014)01-0001-06

10.3969/j.issn.1008-5513.2014.01.001

2013-12-17.

国家自然科学基金(11201293,71171129);上海市教委科研创新基金(13YZ077);上海市科委地方院校能力建设项目(12510501600).

姚裕丰(1982-),博士,副教授,研究方向：李理论及表示理论.

2010 MSC:15A12,15A04