旋转磁导向系统井下磁源优化设计

朱 昱，高德利

（石油工程教育部重点实验室（中国石油大学（北京）），北京102249）

为了满足重力辅助蒸汽驱（SAGD）双水平井定向钻井的施工要求，作为一种新型定位技术的主动式磁定位技术，常被用于确定正钻井相对于参考井（已钻井）的距离和方位。该技术已在石油钻井中得到了广泛应用，包括引导救援井的前进方向、SAGD中双水平井的平行作业、水平井与直井的对穿作业等。国内对该技术的研究起步较晚，研究主要集中于以永磁体为磁源的工具方面，如旋转磁导向系统（rotating magnet ranging system，简称 RMRS）作为一种主动磁测量技术，能够实现直径小于1m的靶区的导航要求，具有较高的精确度［1－2］。

目前，国内对于邻井距离随钻探测技术磁源的设计理论研究较少，主要研究了温度对用于地下磁源所用的永磁体磁性的影响［3］，并初步对磁源的基本设计参数及使用方法进行了介绍［4－6］，但未对磁短节的磁性能进行分析。为了提高磁源性能，笔者以磁源中的永磁体为研究对象，利用电磁场理论推导出了决定永磁体空间磁性能的关键参数，为井下磁源优化设计提供了新思路。

1 磁源短节

磁源短节（也称旋转磁信标）固定于螺杆钻具输出轴上，其末端与钻头相联。在螺杆钻具的驱动下，磁源与钻头一起旋转，在近钻头的空间区域内产生一个动态的旋转磁场，其磁场强度比天然磁场强数百倍至上千倍（相对距离大小而变化），产生的强磁信号可穿透地层数十米，使磁性传感器能捕获信号。在进行双水平井作业时，安装在探管内的传感器对磁源所产生的人工磁场进行测距，根据磁场的矢量参数，可精确计算出井眼轨迹，对钻头所处的当前位置进行精确定位，得到2口井间距离参数，及时纠斜纠偏，达到精确控制水平井间距的目的［7－12］。

目前，磁源设计的主要问题是磁源系统产生的磁场强度不够，达不到传感器所需强度要求，导致测量距离大大减小［3］。磁短节的磁场来源于安装于其内的圆柱形永磁体，永磁体的磁感应强度大小决定了磁短节的磁性能。现在，多数RMRS是将圆柱形永磁体均匀安装在无磁短节中作为磁源（见图1），以产生足够强大的磁场。

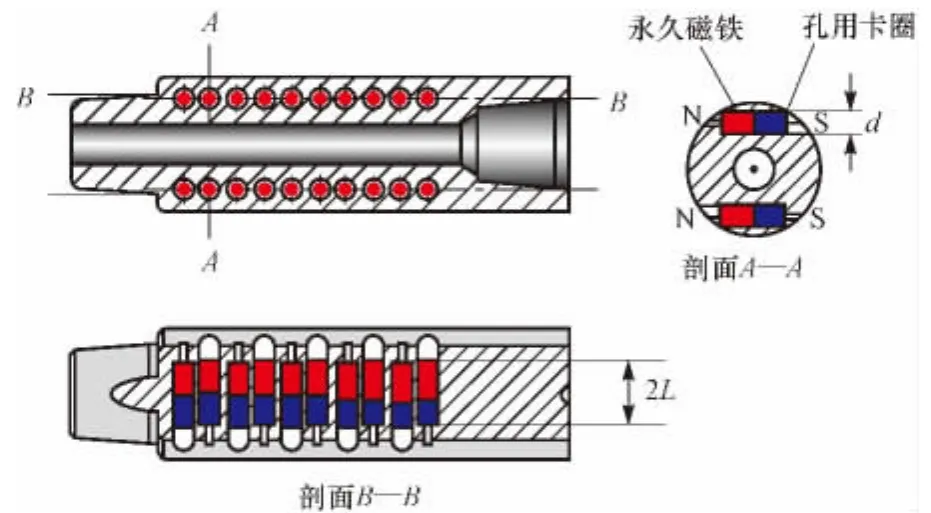
图1 RMRS用磁短节剖面结构Fig.1 The magnetic sub of RMRS

从图1可以看出，圆柱形永磁铁安装在磁短节的永磁体仓内，根据其尺寸和其安装在磁短节上的位置，可以得到永磁体的2个主要参数：圆柱永磁体截面直径和圆柱永磁体长度。

2 永磁体数学模型及计算

2.1 理论分析

在静磁场理论中，有2种完全等效的永磁体计算物理模型：磁荷模型和电流模型。磁荷模型是将磁路中磁体的作用看作是由密度为ρ的分布磁铁产生的，而电流模型是将磁体的作用看作是由密度为J的分布圆电流产生的［13］。与之相对应，在工程计算领域，永磁体外部空间磁场的计算方法分为标量磁位法和矢量磁位法。这2种方法都是从麦克斯韦方程组出发，通过引入磁标量势或磁矢量势，导出有关磁标量势和磁矢量势的微分方程组，进而采用有限元法或者边界法进行数值求解。应该指出的是，引入标量磁位的概念，只是为了使磁场问题求解变得简单，并无物理意义。为了更好地体现计算过程和结果的物理意义，笔者采用矢量磁位法求解计算。

根据磁偶极子理论以及磁介质中静磁场的性质可知，磁介质被磁化后，其中的磁场由外磁场和分子电流产生的磁场叠加而成。为此，将单位体积内分子电流的矢量和称为磁化强度，记为M。根据磁量磁位计算公式［14］，可以得到由磁化强度表示的永磁体矢量磁位计算公式：

式中：A为永磁体矢量磁位，Gs·m；μ0为真空磁导率，0.47μH／m；V为永磁体的体积，m3；S为包围永磁体所有体积的封闭曲面，m2；en为外法向单位矢量Δ称为束缚体电流密度，记为Jb，A／m2；M×en称为束缚面电流密度，记为Jbs，A／m2；R为从磁源到空间点的距离，m。

式（1）可以改为如下形式：

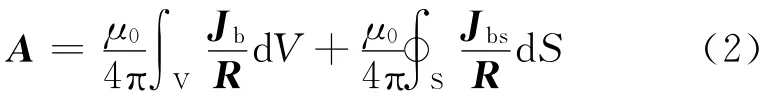
由式（2）可以看出，只要知道永磁体的束缚面电流和束缚体电流密度，就可以求出磁矢量，进而求出磁感应强度。

2.2 永磁体电流模型及计算

取长度为2L的匀磁化圆柱体圆棒，其轴线沿着z轴放置（见图2），由Biot－Savart定律和对称性可知，在空间球坐标中距离r和方位角θ相同的点，磁感应强度大小相同。已知圆柱形磁棒的磁化强度为M＝M0ez，表示该磁棒磁场方向是沿着z轴单位体积内磁矩矢量和为M0。对圆柱上下表面和侧面以及圆柱体进行矢量计算，可得：

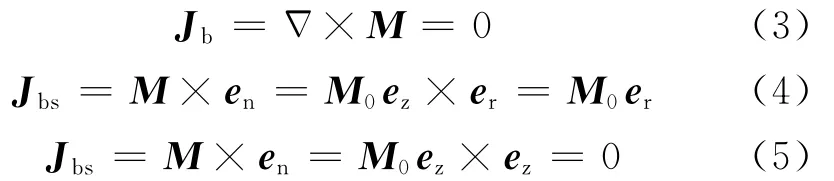
其中，式（3）表示圆柱形永磁体内的束缚体电流密度为0；式（4）表示圆柱侧面存在一个等效束缚面电流密度，大小为M0；式（5）表示圆柱上下表面等效束缚面电流密度为0。因此，该均匀磁化的永磁体可以等效为一个载有沿周向流动的电流密度为M0的薄圆柱面，而圆柱形磁棒上下端面没有束缚面电流存在，如图2所示。根据毕奥－萨伐定律，可以计算出永磁体空间磁场。

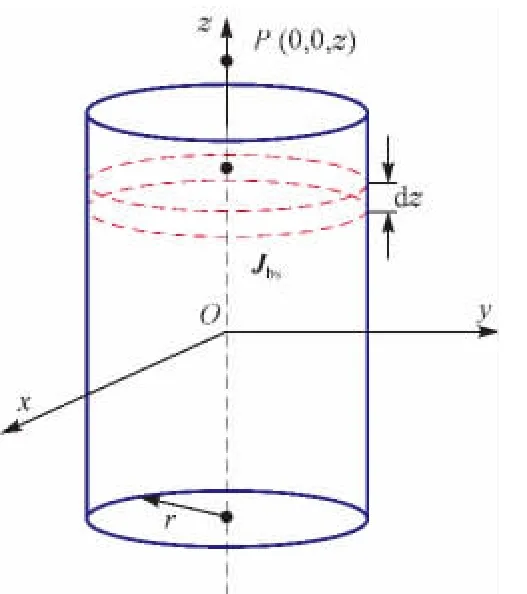
图2 圆柱形永磁体模型Fig.2 The cylindrical permanent magnet model

为了分析磁场磁感应强度随距离的变化，并根据载流线圈在空间的磁场分布规律［13，15］，选择永磁体轴线上的磁场为研究对象。因为在轴线上的磁感应强度最强而且只有z轴分量，而没有x，y轴分量，所以无需进行矢量合成运算。环形电流微元在轴线处产生的磁感应强度为［14］：式中：B为磁感应强度，Gs；r为圆柱永磁体截面半径，m；M0为永磁体等效束缚面电流密度，A／m2；z0为圆柱体磁棒外轴线上点P（0，0，z0）的z轴坐标，m。

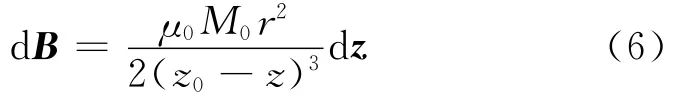
式（6）的积分形式为：

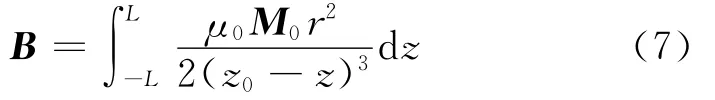
积分后得到：

式中：L为圆柱永磁体长度的一半，m。

从式（8）可以看出，B会随着r2的增大而增大，二者是单调递增关系；同时，可以证关于L的单调递增函数。所以，当永磁体的磁化强度和空间点位置都固定后，增大圆柱形永磁体长度和永磁体截面直径，都可以增强永磁体空间的磁场强度。

3 磁感应强度试验系统

试验系统由空间磁场产生装置和空间磁场采集装置组成。其中，空间磁场产生装置由装有永磁体的磁短节和试验用小车组成，试验时，小车带动磁短节旋转产生空间磁场；空间磁场采集装置由HMR2300三轴高斯计和配套磁场信号采集软件组成，负责采集空间磁场信号。

试验所用永磁体均为圆柱形，可根据需要选择不同直径的永磁体；此外，试验用单根永磁体可由多个相同永磁体拼接而成，达到试验所要求的调节圆柱形永磁体截面直径和长度的目的。试验用磁短节由无磁材料制成，包含12个永磁体仓，永磁体在其内平行交错放置。试验时，使用电机带动磁短节一起旋转，产生与RMRS作业时一样的旋转磁场，以供测量使用。

试验过程中，为了消除地磁场及其他磁场的干扰，采用换向测量的方法。当磁短节上所有圆柱永磁体N极正对传感器时（见图3（a）），根据叠加原理，此时测得的磁场就是磁短节N极的最大磁场与稳恒磁场之和，记为B＋；同理，当磁短节上所有S极正对传感器时（见图3（b）），测得S极的最大磁场和稳恒磁场之和，记为B－。

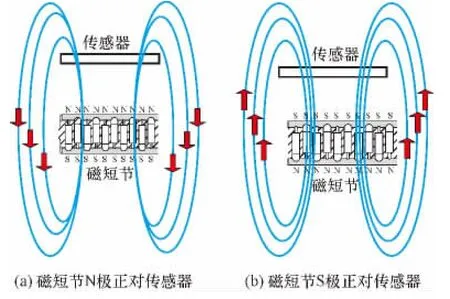
图3 磁场叠加示意Fig.3 Schematic diagram of magnetic field overlap

设地磁场及其他稳恒磁场为Bc。于是，B＋和B－可以表示为：

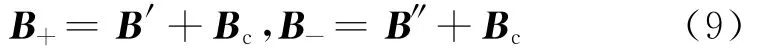
式中：B′为磁短节N极最大磁场，Gs；B″为磁短节S极最大磁场，Gs；Bc为地磁场及其他稳恒磁场，Gs。

根据磁短节设计参数可知，二者大小相等方向相反，所以：

由式（9）和（10）可以得出：

通过以上方法，可以消除包括地磁场在内的稳恒磁场的干扰。在实际施工中，RMRS现场作业所用磁短节安装在钻头后部随钻头一起旋转产生动态磁场，可以消除地磁场的干扰。为了使试验条件与现场条件一致，使用无磁材料制成的试验小车带动试验磁短节一起旋转，模拟RMRS的井下磁短节的旋转；同时利用HMR2003三轴高斯计记下固定点位置的磁感应强度值。为了保证试验结果的有效性，试验所用的永磁体磁化强度保持一致。

HMR2003记录软件可以采集动态条件下磁场的空间直角坐标系中3个轴上的磁感应强度。当磁短节均匀旋转时，测得的磁感应强度的动态采集结果为一条正弦曲线，如图4所示。曲线的波峰值和波谷值即为该点处磁短节磁感应强度的极值B＋和B－，之后利用式（11）即可求出磁短节在该点处的磁感应强度值B′。

4 磁感应强度的影响因素

4.1 永磁体半径

永磁体长度固定为100mm，磁短节中心与传感器距离为4m，永磁体半径为5～10mm，每次增加1mm，测得永磁体磁感应强度与半径的关系曲线（见图5）。由式（8）可知，传感器测得的空间磁感应强度会随着永磁体半径的增大而增大。由图5可见，随着永磁体半径的增大，空间上一点的磁感应强度是增大的。

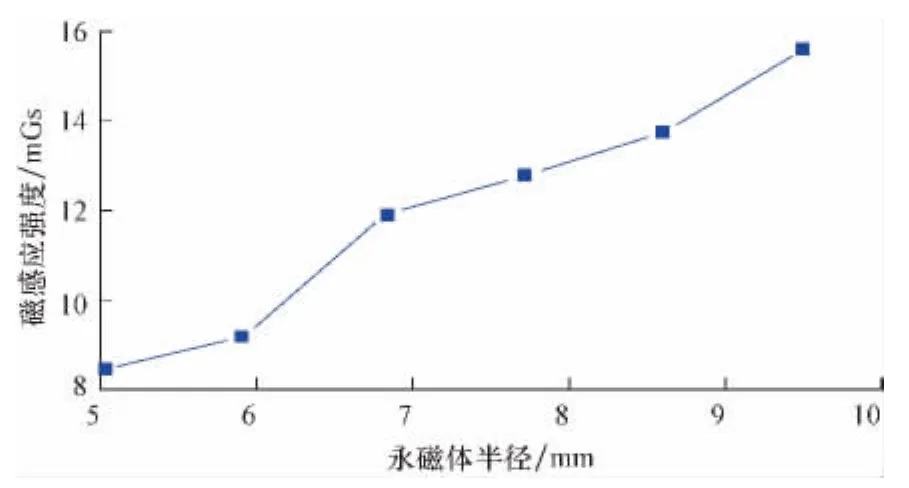
图5 圆柱形永磁体截面半径与磁场强度关系Fig.5 The relationship between the radius of the permanent magnet and the magnetic intensity

4.2 永磁体长度

圆柱形永磁体半径固定为5mm，永磁体长度变化范围为50～100mm，每次长度增加5mm，测得永磁体磁感应强度与长度的关系曲线（见图6）。由图6可见，随着长度的增大，试验测得永磁体在空间上一点的磁感应强度是增大的。

图6 永磁体长度与磁场强度关系曲线Fig.6 The relationship between the length of the permanent magnet and the magnetic intensity

4.3 永磁体长度与直径之比

从以上试验可以看出，增大永磁体截面直径和长度均可以增大其空间磁场的磁感应强度。为了比较二者对空间磁场的影响程度，在永磁体体积相同情况下，对长度和直径不同的永磁体空间磁感应强度进行对比。为了方便对比，将永磁体长度与其直径的比值定义为一个参考值，简称长直比。4组永磁体的几何参数和长直比见表1。

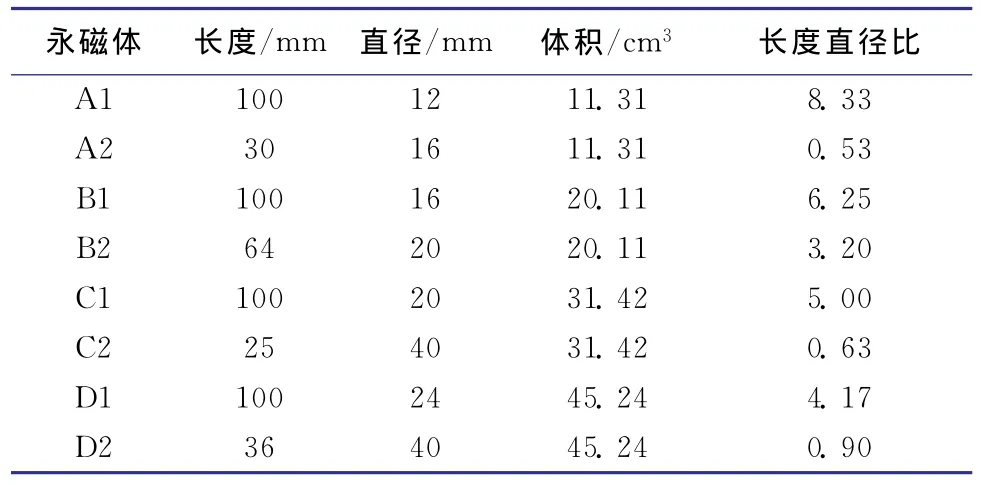
表1 等体积永磁体的几何参数Table 1 Length－to－diameter ratio of the permanent magnet with the same volume

根据式（8），计算相同体积的2个永磁体在空间沿着永磁体轴线上若干相同点的感应强度，结果如图7所示。

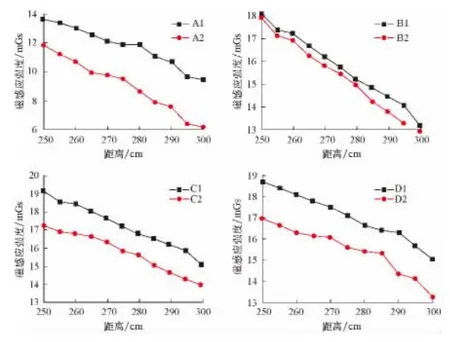
图7 四组永磁体的磁感应强度对比Fig.7 The comparison of results of four groups of magnets

计算结果表明，相同体积条件下，长直比大的永磁体在空间的磁感应强度要大于长直比小的永磁体。

5 磁短节性能测试

将磁短节固定在小车上，选取需要测量的空间平面，在平面上标注好位置，取x方向每次步进10cm和y方向上固定距离5m（SAGD双水平井间距）为测量范围，然后利用高斯计或井下探管测量平面上每个标注位置点的磁感应强度值（见图8）。

分别取3组长度为100mm但直径不等的永磁体（每次12根）放入磁短节，测试并记录每一组不同位置的磁感应强度，并对第1点到第10点的测量值进行对比，结果如图9所示。

分别取3组直径为20mm但长度不等的永磁体（每次12根）放入磁短节，测试并记录每一组不同位置的磁感应强度，并对第1点到第10点的测量值进行对比，结果如图10所示。

图8 磁短节试验示意Fig.8 The schematic diagram of magnetic sub test

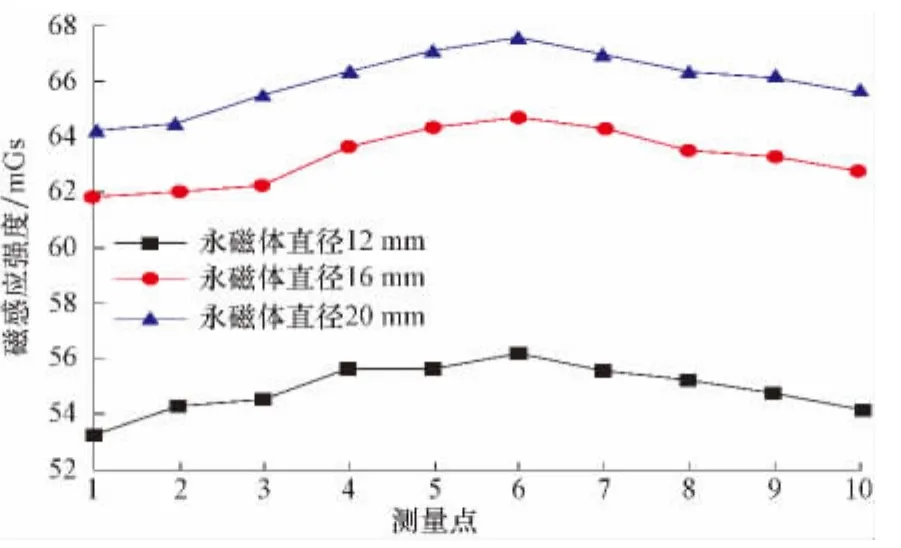
图9 不同直径永磁体对磁短节性能影响Fig.9 The performance of magnetic sub with different magnet diameter

图10 不同长度永磁体对磁短节性能影响Fig.10 The performance of magnetic sub with different magnet length

分别取体积相同而长度与直径之比不同的永磁体（每次12根）放入磁短节，测试并取记录到的第1点到第10点的磁感应强度值，结果如图11所示。

从图9—图11可以看出，长度相同直径不同的永磁体，其空间磁感应强度随着单个永磁体直径的增大而增大；直径相同长度不同的永磁体，其空间磁感应强度随着单个永磁体直径的增大而增大；在相同体积条件下使用长直比大的永磁体，可以大大提高磁短节的空间磁感应强度。

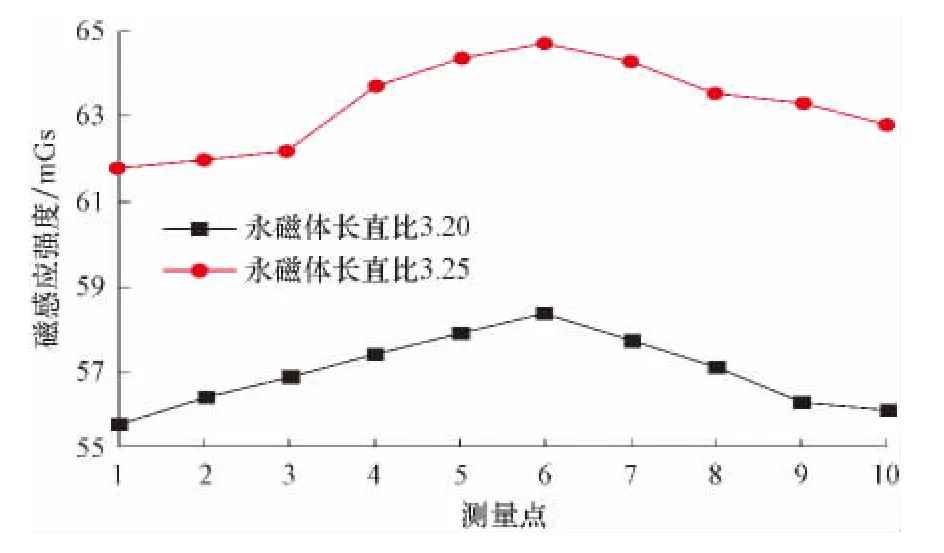
图11 不同长直比永磁体对磁短节性能影响Fig.11 The performance of magnetic sub with different magnet length－to－diameter ratio

6 结 论

1）计算和试验结果表明，在磁短节设计尺寸不变的情况下，对永磁体的几何参数进行优化设计，可以提高磁源短节的磁性能。

2）井下磁源是旋转导向系统的关键部件，其设计尺寸主要受到井眼空间尺寸的限制。所以，如何在有限空间内优化磁短节的磁性能，是提高旋转导向磁定位质量的关键。

3）将该理论引入实际应用的关键是如何利用数值模拟和物理模拟找到永磁体和磁短节的最佳匹配值，这也是下一步研究的方向。

［1］胡汉月，陈庆寿.RMRS在水平井钻进中靶作业中的应用［J］.地质与勘探，2008，44（6）：89－92.Hu Hanyue，Chen Qingshou.RMRS application on target－hitting of horizontal drilling［J］.Geology and Prospecting，2008，44（6）：89－92.

［2］Kylingstad A，Halsey G W.Magnetic ranging tool accurately guides replacement well［J］.Oil ＆ Gas Journal，1992，90（51）：96－99.

［3］宋盼.地下磁导航系统的磁源设计［D］.南昌：南昌航空大学测试与光电工程学院，2010.Song Pan.Magnetic source design of rotary magnetic ranging system［D］.Nanchang：Nanchang Hangkong University，School of Measuring and optical Engineering，2010.

［4］王德桂，高德利.管柱形磁源空间磁场矢量引导系统研究［J］.石油学报，2008，29（4）：609－611.Wang Degui，Gao Deli.Study of magnetic vector guide system in tubular magnet source space［J］.Acta Petrolei Sinica，2008，29（4）：609－611.

［5］姚林，樊华.RMRS测距仪在延平1水平连通井组中的应用［J］.油气藏评价与开发，2011，1（6）：76－80.Yao Lin，Fan Hua.The application of RMRS rangefinder in the horizontal connected well group of Yanping－1［J］.Reservoir E－valuation and Development，2011，1（6）：76－80.

［6］陈若铭，陈勇，罗维，等.MGT导向技术在SAGD双水平中的应用及研制［J］.新疆石油天然气，2011，7（3）：25－29.Chen Ruoming，Chen Yong，Luo Wei，et al.Application of magnetic guidance technology in SAGD double horizontal well and development［J］.Xinjiang Oil ＆ Gas，2011，7（3）：25－29.

［7］Al－Khodhori S，Al－Riyami H，Holweg P，et al.Connector conductor wells technology in brunei shell petroleum achieve high profitability through multi－well bores and downhole connections［R］.SPE 111441，2008.

［8］杨明合，夏宏南，屈胜元，等.磁导向技术在SAGD双水平井轨迹精细控制中的应用［J］.钻采工艺，2010，33（3）：12－14.Yang Minghe，Xia Hongnan，Qu Shengyuan，et al.MGT system applied to accuracy well tracks controlling in SAGD horizontal twin wells［J］.Drilling ＆Production Technology，2010，33（3）：12－14.

［9］韩志勇.定向钻井设计与计算［M］.东营：中国石油大学出版社，2007：5－47.Han Zhiyong.Design and calculation of directional drilling［M］.Dongying：China University of Petroleum Press，2007：5－47.

［10］谢川.一种基于磁强计和倾角传感器的钻井测斜仪［J］.仪器仪表学报，2010，31（10）：2357－2362.Xie Chuan.Clinometer for artesian well based on magnetometer and inclination angle sensor［J］.Chinese Journal of Scientific Instrument，2010，31（10）：2357－2362.

［11］李番军.连续测斜仪研究［D］.哈尔滨：哈尔滨工业大学电气工程及自动化学院，2006.Li Fanjun.The research of inclinometer［D］.Harbin：Harbin Institute of Technology，School of Electrical Engineering and Automation 2006.

［12］刘修善，王继平.基于大地测量理论的井眼轨迹监测方法［J］.石油钻探技术，2007，35（4）：1－5.Liu Xiushan，Wang Jiping.A method for monitoring wellbore trajectory based on the theory of geodesy［J］.Petroleum Drilling Techniques，2007，35（4）：1－5.

［13］周希朗.电磁场［M］.北京：电子工业出版社，2008：40－42.Zhou Xilang.Electromagnetic Field［M］.Beijing：Publishing House of Electronics Industry，2008：40－42.

［14］劳兰P，考森D R.电磁场与电磁波［M］.北京：人民教育出版社，1980：98－109.Lorrain P，Corson D R.Electromagnetic fields and waves［M］.Beijing：People Education Press，1980：98－109.

［15］倪光正，杨仕友，邱捷，等.工程电磁场数值计算［M］.北京：机械工业出版社，2012：76－90.Ni Guangzheng，Yang Shiyou，Qiu Jie，et al.Numerical computations of electromagnetic fields［M］.Beijing：China Machine Press，2012：76－90.