泥页岩地层水力裂缝延伸方位研究

邵尚奇，田守嶒，李根生，盛 茂

（油气资源与探测国家重点实验室（中国石油大学（北京）），北京102249）

随着油气资源需求量的增大，非常规油气藏（页岩气、致密气等）的开发得到了极大的重视。由于泥页岩地层具有低孔、低渗、天然裂缝发育的特点［1］，因此非常规油气藏的开发需要借助水力压裂。国外学者对泥页岩地层的裂缝延伸进行了大量研究，提出了很多裂缝起裂延伸准则：Erdogan等人［2］提出了最大轴向应力准则（MTS准则）；Palaniswamy等人［3］提出了能量释放速率准则；Sih等人［4－6］提出了应变能密度因子理论。这些准则均是基于线弹性断裂力学提出的［7］。但泥页岩不同于砂岩等脆性岩石，研究表明，泥页岩受到一定应力作用时会发生蠕变，且随着周围载荷的增大，泥岩从脆性向塑性转变［8－11］，所以，线弹性断裂力学理论并不适用于泥页岩地层水力裂缝延伸的研究。因此，笔者基于塑性断裂力学理论，根据应力叠加原理以及T准则，建立了水力裂缝起裂角解析模型，计算了不同裂缝与最大水平主应力方向夹角以及施工压力下水力裂缝的起裂角，分析了这些参数对水力裂缝起裂的影响规律。

1 水力裂缝起裂角分析

1.1 塑性区域计算

泥页岩地层的裂缝端部存在着塑性区，而塑性区的存在可以阻止脆性断裂裂缝的扩展。假设裂缝周围塑性核区域半径是变化的，裂缝沿着最大体积应变能密度方向延伸，当体积应变能密度达到临界值时，裂缝开始延伸。利用叠加原理［12］分析裂缝端部应力场，如图1所示。

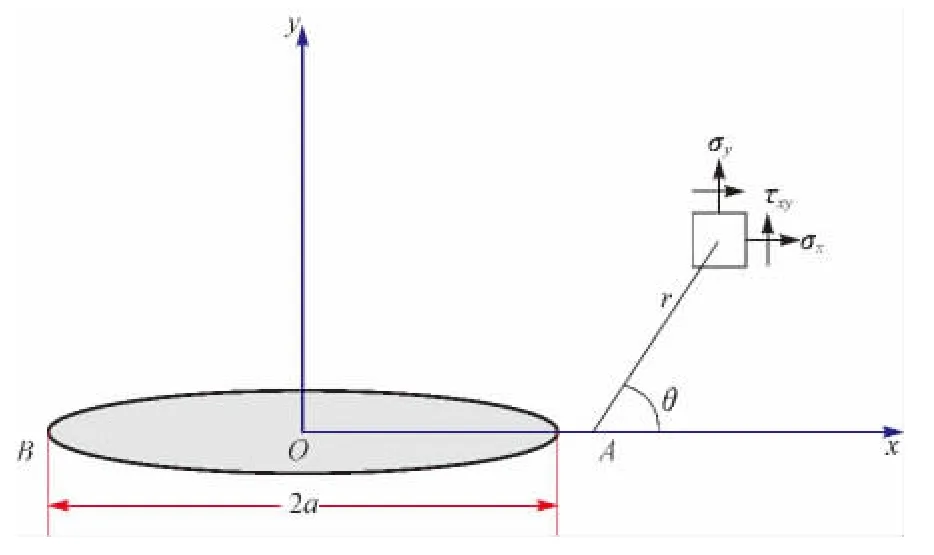
图1 裂缝端部应力场的极坐标示意Fig.1 The stress field of fractures under polar coordinate

不同方向应力分量的计算公式为：

式中：σx，σy和τxy分别为裂缝端部的应力分量，MPa；KⅠ和KⅡ分别为Ⅰ型和Ⅱ型应力强度因子，MPa·m1／2；r为极坐标下任意一点与裂缝的距离，m；θ为极坐标下任意一点与裂缝长轴的顺时针夹角，（°）；a为裂缝半缝长，m。

裂缝端部周围的体积应变能密度TV和形状应变能密度TD的表达式为：

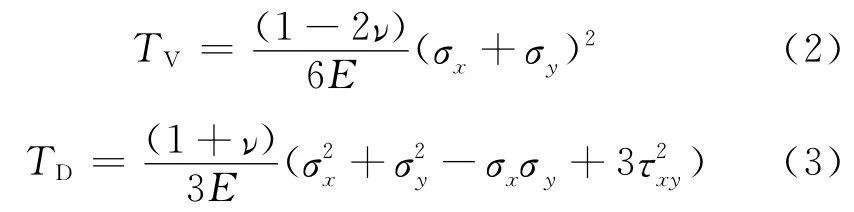
式中：ν为泊松比；E为弹性模量，MPa。

式（3）可以表示为：

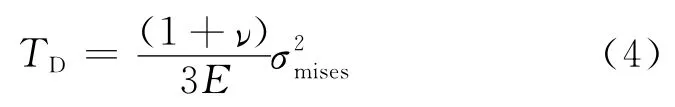
式中：σmises为von Mises应力，MPa。

在裂缝周围塑性核区域的边界上，von Mises应力是相等的［13］，所以，可以认为裂缝塑性区域边界上的形状应变能密度是常数［14］。

当塑性区域上的体积应变能密度TV达到Ⅰ型断裂应变能的临界值时，裂缝开始失稳延伸，即：

式中：TVc为体积应变能密度的临界值，MPa。

将式（1）代入式（3），得到裂缝端部塑性核半径R的表达式：

1.2 起裂角计算

在地层岩石中，水力裂缝端部附近区域存在塑性区域，而离裂缝端部较远的区域是弹性地层。因此，水力裂缝首先要穿过塑性区域，然后到达弹性区域（见图2）。T准则假设裂缝会沿着裂缝尖端至弹塑性边界距离最小的方向延伸，如图2中红线所示。当边界的总应变能达到应变能临界值时，裂缝开始起裂扩展。

假设裂缝端部的塑性区域是连续的，则裂缝延伸起裂角的表达式为：

将式（6）带入式（7），得到起裂角的计算公式：

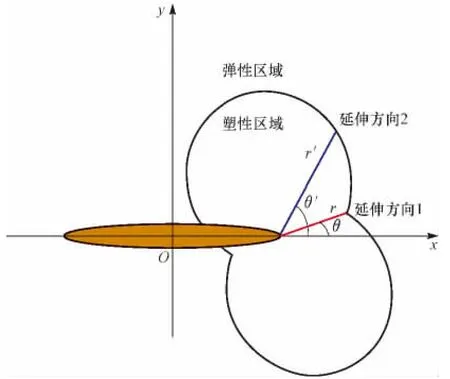
图2 塑性地层裂缝延伸方向示意Fig.2 The propagating direction of fracture in ductile formation

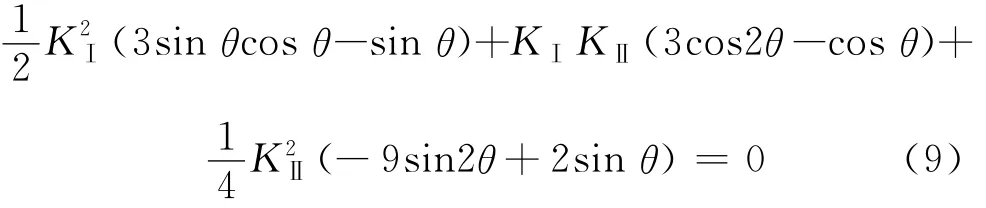
对式（9）求解，即可得到水力裂缝的起裂角。

2 Ⅰ－Ⅱ型复合裂缝塑性区域研究

水平井进行分段射孔压裂时，由于钻井设备以及地质条件复杂等原因，导致钻进的方向不平行于最小水平主应力方向，而是与最小水平主应力方向存在一定的倾角（见图3），此时裂缝处于拉剪应力状态。假设裂缝处于无限大平面内，周边岩体为均质材料。图3中，σH，σh分别为加载在裂缝上的最大水平主应力和最小水平主应力；σn，τn分别为作用在倾斜裂缝表面上的正应力和剪应力；p为裂缝内流体压力，γ为水力裂缝和最大水平主应力方向的夹角。

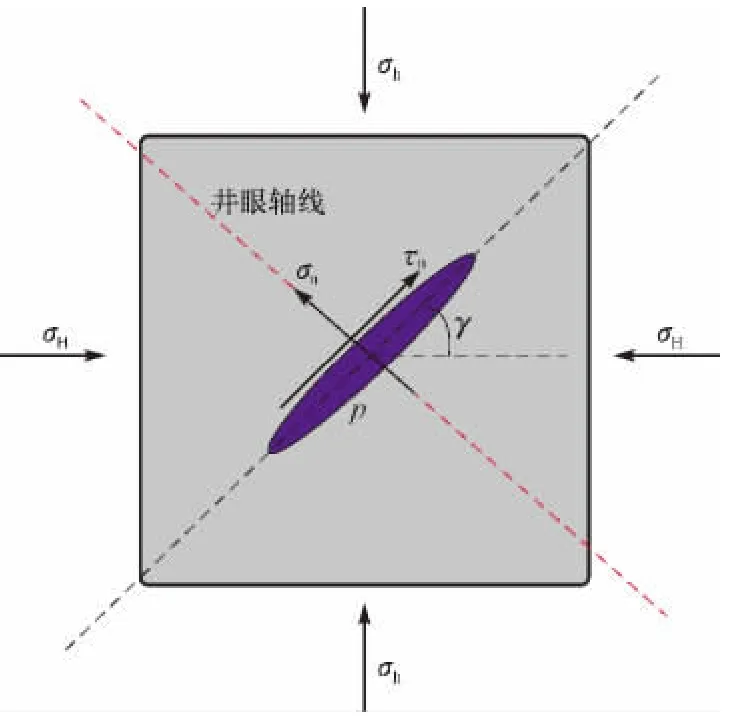
图3 地应力和流体压力作用下Ⅰ－Ⅱ型复合裂缝示意Fig.3 Ⅰ－Ⅱ mixed mode fracture under in－situ stress and fluid pressure

水力裂缝应力强度因子的表达式为：

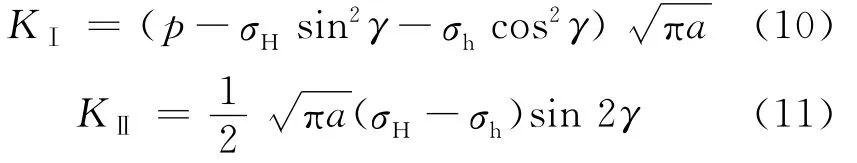
取裂缝缝内流体压力p为50MPa，最大水平主应力σH为60MPa，最小水平主应力σh为40MPa。将其代入式（10）和式（11），可以计算出不同裂缝与最大水平主应力方向夹角下的应力强度因子KⅠ和KⅡ；将KⅠ和KⅡ代式（9）即可计算出起裂角，将计算出的起裂角代入式（6）即可计算出塑性核半径，结果见图4。

由图4可以看出，水力裂缝与最大水平主应力方向夹角不同，水力裂缝的塑性区域包络线所包含的区域也发生改变。当水力裂缝与最大水平主应力方向夹角为0°和90°时，缝端塑性区域沿裂缝长轴方向对称分布，且分布范围为0～0.18倍半缝长；当水力裂缝与最大水平主应力方向夹角为30°和60°时，裂缝塑性区域沿裂缝不对称分布，分布范围为0～0.45倍半缝长。这是因为，当裂缝和最大水平主应力方向夹角为0°和90°时，裂缝面只受到拉应力的作用，裂缝面上不存在剪应力，起裂方向和裂缝平行，塑性区域沿缝长方向对称分布；而当裂缝与最大水平主应力方向夹角为30°和60°时，裂缝面同时受到拉应力和剪应力作用，延伸方向与裂缝呈一定的角度，塑性区域不沿裂缝方向对称分布。

3 起裂角敏感性分析

3.1 裂缝与最大水平主应力方向夹角

对利用塑性准则和最大周向应力准则计算出的起裂角（见图5）进行比较，可以看出，缝内流体压力一定，当裂缝与最大水平主应力方向夹角为0°～90°时，水力裂缝的起裂角为0°～180°，且起裂角随裂缝与最大水平主应力方向夹角的增大逐渐减小，而起裂角越大，井筒周围的裂缝越容易发生扭曲和转向；裂缝与最大水平主应力方向夹角为0°～65°时，利用塑性准则计算出的起裂角比利用最大周向应力准则计算出的大0°～20°，这是因为水力裂缝受到的拉应力较大，占据主导地位，塑性区域内的应变能较大，裂缝起裂角较大；当裂缝与最大水平主应力方向夹角超过65°时，利用塑性准则和最大周向应力准则计算出的起裂角相差不大，这是由于随着裂缝与最大水平主应力方向夹角的增大，水力裂缝的拉应力和剪应力逐渐减小，塑性区域内的应变能减小，起裂角也随之减小。

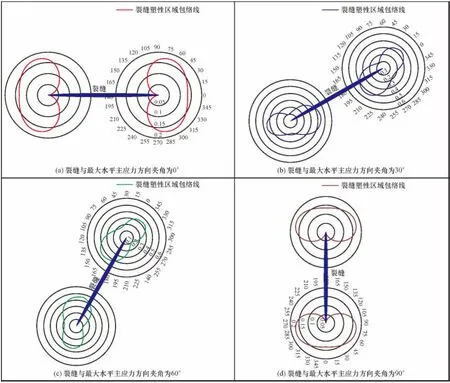
图4 地应力条件下不同裂缝与最大水平主应力方向夹角水力裂缝塑性区域计算结果Fig.4 Plastic region of hydraulic fracture under different inclination angle of fracture and maximum horizontal principal stress with in－situ stress

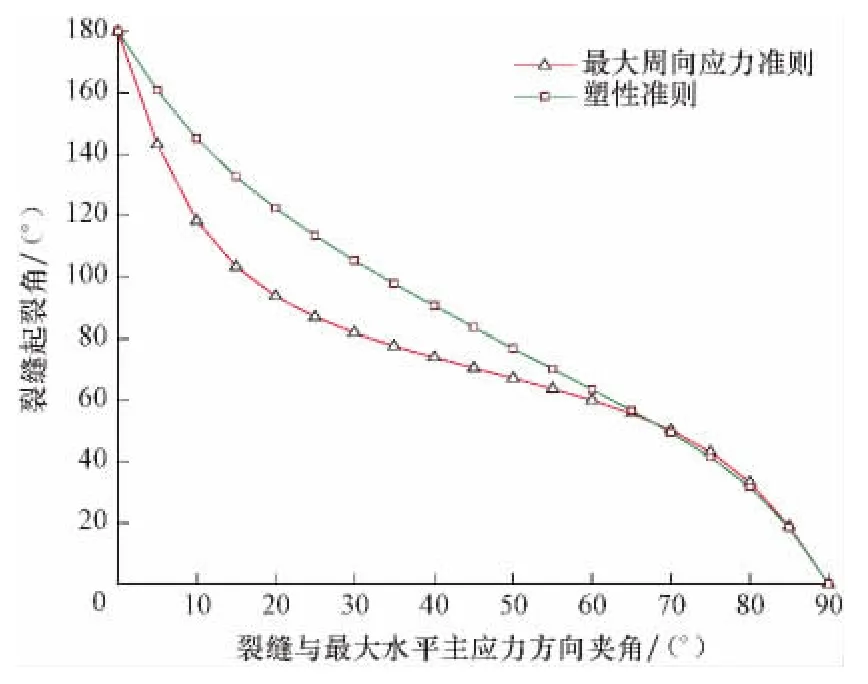
图5 利用最大周向应力准则和塑性准则计算出的起裂角Fig.5 Comparison of fracture initiation angle calculated by maximum circumferential stress criterion and ductile criterion

3.2 缝内压力

在水平井分段射孔压裂时，由于每一段的施工压力存在差异，导致了裂缝的几何形状各不相同，起裂角也不一样。假设其他条件不变，计算不同缝内流体压力下的起裂角，结果见图6。

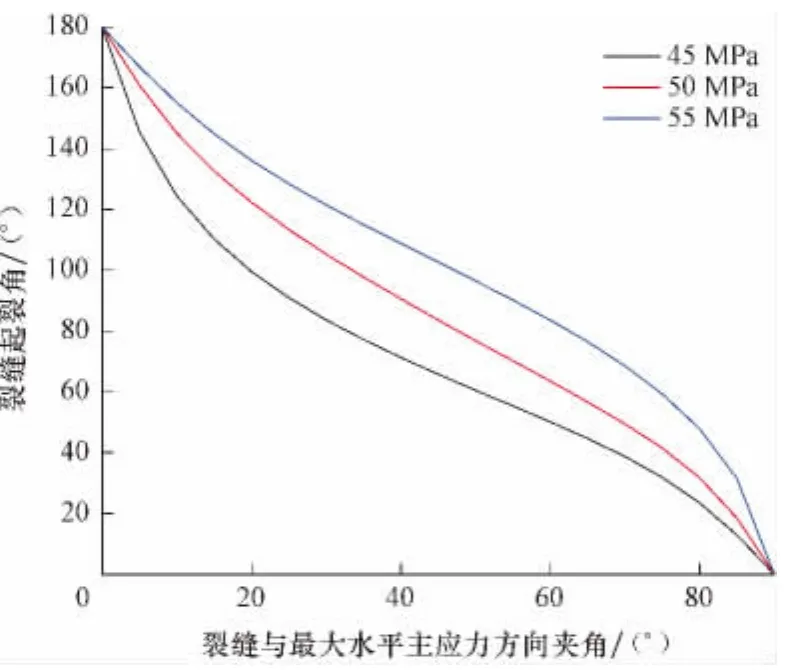
图6 不同缝内流体压力下的裂缝起裂角变化Fig.6 Comparison of fracture initiation angles under different fluid pressures

从图6可知，当裂缝与最大水平主应力方向夹角一定时，缝内流体压力越大，裂缝的起裂角也越大。这是因为缝内流体压力越大，塑性区域的体积膨胀应变能密度越大，导致起裂角增大。这一规律可以解释在水力压裂施工中，当施工压力过高时，近井筒地带的裂缝容易发生转向，使近井筒的表皮系数增大，油气产能降低。

4 结 论

1）推导出了Ⅰ－Ⅱ型复合裂缝的缝端塑性核半径和起裂角表达式。

2）起裂角随裂缝与最大水平主应力方向夹角的增大而减小，随缝内流体压力的增大而增大。

3）在低施工排量下压出的裂缝和与最大水平主应力方向夹角较大的裂缝比较平直，而在高排量压出的裂缝和与最大水平主应力方向夹角较小的裂缝容易发生转向。

［1］丁文龙，许长春，久凯，等.泥页岩裂缝研究进展［J］.地球科学进展，2011，26（2）：135－144.Ding Wenlong，Xu Changchun，Jiu Kai，et al.The research progress of shale fractures［J］.Advances in Earth Science，2011，26（2）：135－144.

［2］Erdogan F，Sih G C.On the crack extension in plates under plane loading and transverse shear［J］.Journal of Basic Engineering，1963，85（4）：519－525.

［3］Palaniswamy K，Knauss W G.On the problem of crack extension in brittle solids under general loading［J］.Mechanics Today，1978，4（30）：87－148.

［4］Sih G C.Some basic problems in fracture mechanics and new concepts［J］.Engineering Fracture Mechanics，1973，5（2）：365－377.

［5］Sih G C.Strain－energy－density factor applied to mixed mode crack problems［J］.International Journal of Fracture，1974，10（3）：305－321.

［6］Sih G C.A special theory of crack propagation［J］.Mechanics of Fracture Initiation and Propagation Engineering Applications of Fracture Mechanics，1973，10：1－22.

［7］Whittaker B N，Singh R N，Sun G.Rock fracture mechanics［M］.London：Elsevier，1992：21－22.

［8］李杭州，廖红建，孔令伟，等.膨胀性泥岩应力－应变关系的试验研究［J］.岩土力学，2007，28（1）：107－110.Li Hangzhou，Liao Hongjian，Kong Lingwei，et al.Experimental study on stress－strain relationship of expansive mud－stone［J］.Rock and Soil Mechanics，2007，28（1）：107－110.

［9］李荣，孟英峰，罗勇，等.泥页岩三轴蠕变实验及结果应用［J］.西南石油大学学报，2007，29（3）：57－59.Li Rong，Meng Yingfeng，Luo Yong，et al.Triaxial creep test of mudstone and the result application［J］.Journal of Southwest Petroleum University，2007，29（3）：57－59.

［10］刘钦，李术才，李利平，等.软弱破碎围岩隧道炭质页岩蠕变特性试验研究［J］.岩土力学，2012，33（增刊2）：21－28.Liu Qin，Li Shucai，Li Liping，et al.Experimental study of carbonaceous shale creep characters of weak broken surrounding rock tunnel［J］.Rock and Soil Mechanics，2012，33（supplement 2）：21－28.

［11］许宝田，阎长虹，许宏发.三轴试验泥岩应力－应变特性分析［J］.岩土工程学报，2004，26（6）：863－865.Xu Baotian，Yan Changhong，Xu Hongfa.Triaxial tests on stress－strain of mud stone［J］.Chinese Journal of Geotechnical Engineering，2004，26（6）：863－865.

［12］Khan S，Khraisheh M K.A new criterion for mixed mode fracture initiation based on the crack tip plastic core region［J］.International Journal of Plasticity，2004，20（1）：55－84.

［13］Shafique M A Khan，Marwan K Khraisheh.Analysis of mixed mode crack initiation angles under various loading conditions［J］.Engineering Fracture Mechanics，2000，67（5）：397－419.

［14］Maiti S K，Smith R A.Comparison of the criteria for mixed mode brittle fracture based on the preinstability stress－strain field：partⅠ：slit and elliptical cracks under uniaxial tensile loading［J］.International Journal of Fracture，1983，23（4）：281－295.