第二类切比雪夫乘积型和式方程的研究

吴国鸿，王珊珊，吴康



第二类切比雪夫乘积型和式方程的研究

吴国鸿，王珊珊，吴康

（华南师范大学 数学科学学院，广东 广州 510631）

定义了第二类切比雪夫乘积型和式方程，用代数变换的方法求解第二类切比雪夫乘积型基本方程、二项乃至多项乘积型和式方程的全体复根，并探讨了其乘积型基本方程的重根规律.

切比雪夫多项式；第二类切比雪夫乘积型和式方程；全体复根；代数变换

切比雪夫多项式是计算数学中一类重要的特殊函数，第一类和第二类切比雪夫多项式起源于多倍角余弦函数和正弦函数的展开式，在工程计算等方面有着广泛应用[1-3]. 本文定义了第二类切比雪夫乘积型和式方程，求解其基本方程以及多项情形的全体复根，并探讨部分重根规律.

1 预备知识

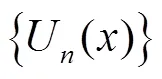
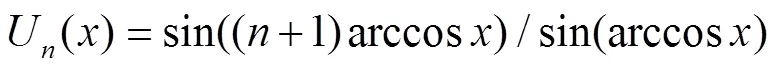
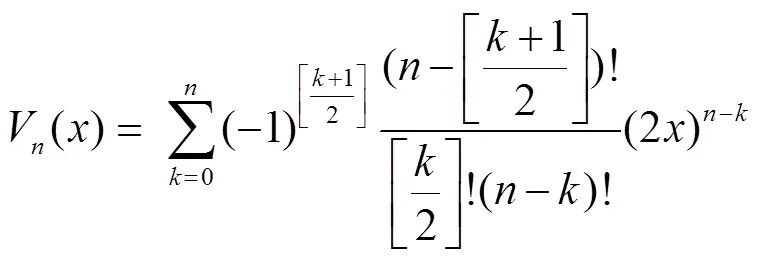
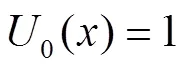
2 第二类切比雪夫乘积型基本方程

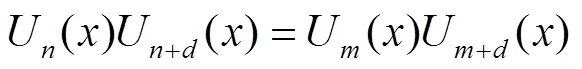
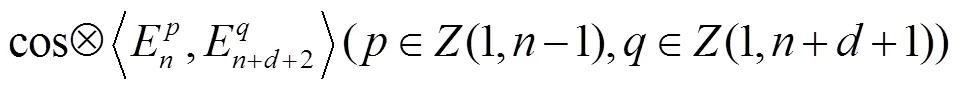
3 第二类切比雪夫乘积型多项和式方程

3.1 二项和式方程

对于以上定义的第二类切比雪夫乘积型二项和式方程，可加上一定条件进行化简求解.

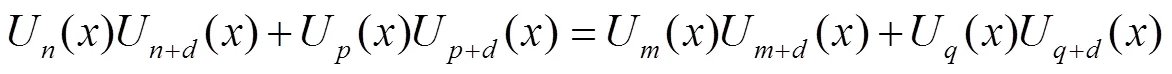
由定义（1）和方程（4）有：

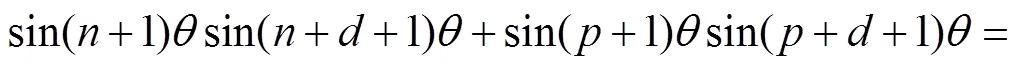
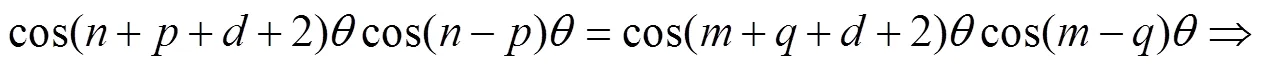
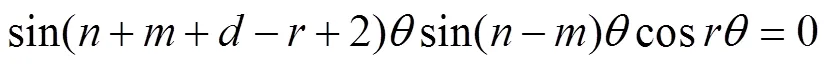
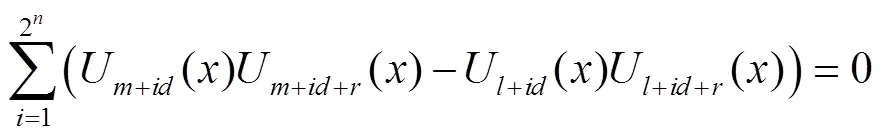
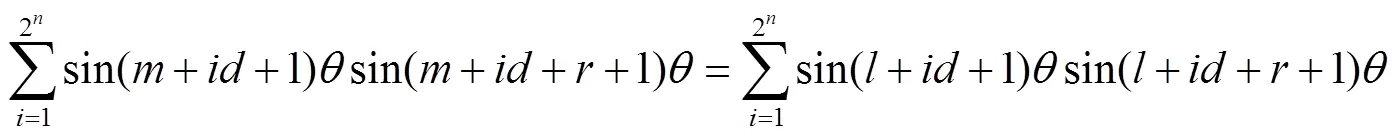
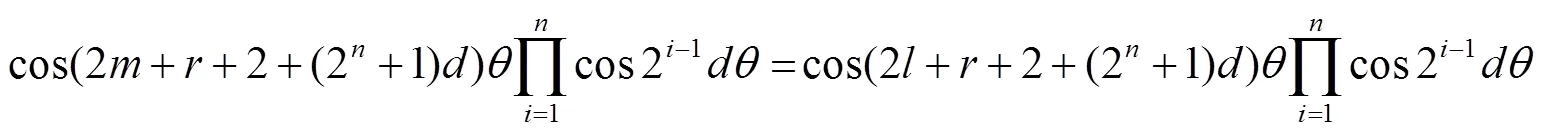
4 第二类切比雪夫乘积型基本方程的重根规律

以下定理给出乘积型基本方程的重根规律，即何时全为单根，何时存在重根及其重根数.

[1] 宫凤强，李夕兵，邓建. 基于第二类切比雪夫多项式的岩土参数概率分布推断[J]. 土工基础，2005(4): 54-57.

[2] 凌明灿，吴康. 第二类切比雪夫多项式和式方程的研究[J]. 河南教育学院学报：自然科学版，2012, 21(4): 11-13.

[3] 凌明灿，吴康. 第二类切比雪夫多项式方程的重根规律[J]. 惠州学院学报：自然科学版，2012, 32(6): 37-39.

[4] 刘式适，刘式达. 特殊函数[M]. 北京：气象出版社，2002: 314-361.

[5] 王中德. 两类新的切比雪夫多项式[J]. 北京邮电学院学报，1989, 12(2): 46-54.

[责任编辑：熊玉涛]

A Study of the Second Chebyshev Sum Equation of Product Form

WUGuo-hong, WANGShan-shan, WUKang

(School of Mathematics, South China Normal University, Guangzhou 510631, China)

The Second Chebyshev sum equation of product form was defined, and the whole complex roots of this type of equation with two and even more items as well as some rules of their re-roots were explored by means of algebraic transformation.

Chebyshev polynomials; the Second Chebyshev sum equation of product form; whole complex roots; algebraic transformation

1006-7302（2014）04-0019-04

O122.2

A

2014-06-19

吴国鸿（1987—），男，广东广州人，在读硕士生，主要研究方向为组合数学、初等数学、竞赛数学.