钢丝绳直线段有限元建模与分析

王斌，史天录，景亚杰



钢丝绳直线段有限元建模与分析

王斌1，史天录1，景亚杰2

（1. 五邑大学 机电工程学院，广东 江门 529020；2. 西安建筑科技大学 材料学院，陕西 西安 710055）

利用Patran软件设计了1×6钢丝绳直线段股和独立绳芯钢丝绳的有限元模型，利用Nastran进行了有限元分析，计算中考虑了一端固定、一端轴向旋转情况下钢丝绳的载荷与应变的关系和股内各钢丝分载荷情况. 对比有限元分析结果、理论计算结果和实验结果发现，三者间误差均在容许范围内，验证了本文有限元模型的有效性.

钢丝绳；应力应变；分载；有限元分析

为研究钢丝绳的失效机理，研究人员不断将新方法、新思路引入对钢丝绳的研究中[1-5]，常见的钢丝种类有1×6钢丝绳、独立钢丝绳芯（Independent Wire Rope Core，IWRC，又称7×7钢丝绳）、Seale 6×19钢丝绳等.由于钢丝绳几何形状复杂，在轴向受载的情况下绳内钢丝的响应复杂且为非线性，传统的钢丝绳数学模型只能在忽略一些因素（如忽略绳内钢丝间的摩擦）下解决钢丝绳的局部特性，只在弹性变形范围内分析钢丝绳受载响应、求解简单的钢丝绳数学模型、分析钢丝间线接触等，而有限元分析方法可以分析钢丝绳受载后复杂响应. 本文通过有限元建模与分析方法，对典型的1×6钢丝绳进行建模分析，并将其应用到结构更复杂的IWRC钢丝绳. 最后，通过将有限元结果与实验结果进行对比，以验证本文所用方法的有效性.

1 1×6钢丝绳有限元分析

1.1 有限元分析前处理

1×6钢丝绳可以作为单独的绳使用，亦可以作为IWRC钢丝绳的绳芯使用，如图1所示. 文献[6]给出了Nastran分析有限元接触问题的有效方法，本文利用文献[7]的钢丝绳参数，将1×6钢丝绳的UG模型导入Patran中，并在钢丝绳几何模型端部加上圆柱形承载端，分析绳内部不同层、不同钢丝的承载比重情况. 由于端部与钢丝接触部位的网格划分复杂，为精简计算，只需将钢丝绳内载荷分配到不同股或丝上.

划分网格时，Nastran接触模型的计算模块（SOL600）只能采用四面体5节点或六面体8节点网格. 由于六面体网格更能有效地对节点进行约束（MPC）[7,8]，并可有效提高钢丝绳有限元分析的精度，因此，本文也沿用六面体8节点有限元网格，但附加圆柱形端部不受网格划分的限制，只需注意网格畸形现象.

图1 钢丝绳几何形状

图2 1×6钢丝绳的有限元模型

处理材料参数时，本文沿用文献[2]的实验数据与文献[7]的有限元数据，钢丝的材料为双线性各向同性材料（bilinear isotropic material），其几何参数与有限元模型参数见表1、2，可以推导出：

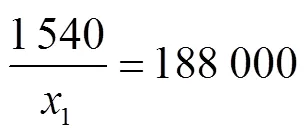
表1 1×6钢丝绳几何参数

表2 1×6钢丝绳有限元模型参数

求解模型时，利用隐式非线性求解器（implicit nonlinear SOL600）求解钢丝绳轴向受载后的接触模型. Nastran提供了Glue和Touch两种接触模型. Glue模型定义简单，符合Costello[1]提出的计算模型，钢丝间没有相对滑动，但位于两接触丝上的各节点会在接触位置附近合并，网格会变形，计算精度低；Touch模型中，侧丝与中心丝间有相对移动，在摩擦系数低的情况下侧丝与中心丝需被定义为接触关系，接触模型定义较复杂，但接触位置网格未变形，计算精度高，本文选用Touch模型. 需要指出的是，Costello的模型理论[1]与Utting的实验[2]已论证了钢丝绳在只受轴向载荷时，摩擦对钢丝轴向应变的影响很小.

1.2 有限元分析结果说明

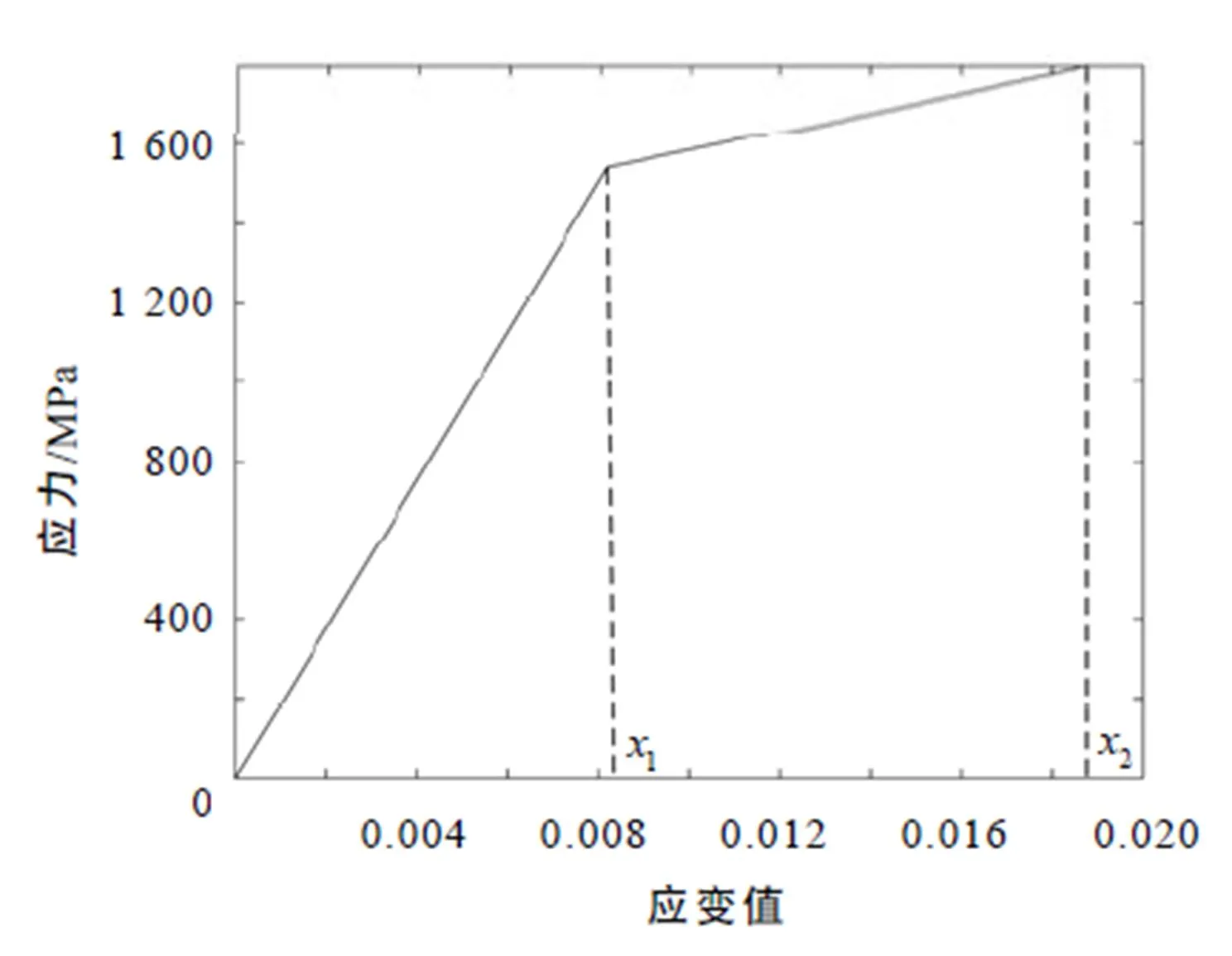
图3 材料的应力—应变曲线

图4 轴向变形结果

图5 端部固定情况下轴向载荷与轴向应变关系

图6 端部固定情况下中心丝承载比重与轴向应变关系

2 IWRC钢丝绳有限元分析

钢丝绳中丝的种类包括：中心股中侧丝和中心丝、侧股中侧丝和中心丝. 侧股可以有多层，侧丝绕中心丝形成简单直股，简单直股绕中心股形成整绳. 如图1，钢丝整绳三维建模时，简单直股（中心股）中侧丝和侧股中心丝可以用简单的一次螺旋线方程来建模，而侧股中侧丝的建模需要复杂的二次螺旋线方程：

图7 IWRC钢丝绳的有限元模型

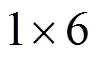
3 总结与展望

本文利用Patran、Nastran有限元分析软件计算了钢丝绳中股及绳在受轴向载荷后的响应，将有限元计算结果与实验结果及理论计算结果进行了对比，验证了有限元分析模型的有效性. 钢丝绳在受载后由于振动、摩擦、过载等因素的影响，其内部中心股和侧股间的点接触应力是决定钢丝绳寿命的主要原因，下一步工作可对接触应力进行分析，将对接触位置附近的有限元网格进行细化调整以提高计算精度.

[1]COSTELLO G A. Theory of wire rope[M]. 2nd Edition. New York: Springer, 1997.

[2] UTTING W S, JONES N. The response of wire rope strands to axial to tensile loads—PART I. Experimental results and theoretical prediction [J]. International journal of mechanical sciences, 1987, 29(9): 605-619.

[3] STANOVA E, FEDORKO G, FABIAN M, et al. Computer modelling of wire strands and ropes part II: Finite element-based applications [J]. Advances in Engineering Software, 2011, 42(6): 322-331.

[4] 浦汉军. 起重机不旋转钢丝绳理论研究及其寿命研究[D]. 广东：华南理工大学，2012.

[5] 王桂兰，孙建芳，张海鸥. 钢丝绳捻制成形的空间几何模型与有限元分析[J]. 应用力学学报，2003, 20(3): 82-87.

[6] 宋祎平，黄勤，刘正瑞. 三环减速器的PATRAN-NASTRAN接触有限元分析探讨[J]. 机械管理开发，2011(3): 34-37.

[7] JIANG Wenguang, YAO M S, WALTON J M. A concise finite element model for simple straight wire rope strand [J]. International Journal of Mechanical Sciences, 1999, 41(2): 143-161.

[8] WANG Dagang, ZHANG Dekun, WANG Songquan, et al. Finite element analysis of hoisting rope and fretting wear evolution and fatigue estimation of steel wires [J]. Engineering Failure Analysis, 2013, 27: 173-193.

[9] IMRAK C E, ERDONMEZ C. On the problem of wire rope model generation with axial loading [J]. Mathematical and Computational Applications, 2010, 15(2): 259-268.

[责任编辑：韦 韬]

Wire Rope Line Segment Finite Element Modeling and Analysis

WANGBin1, SHITian-lu1, JINGYa-jie2

(1. School of Mechanical and Electrical Engineering, Wuyi University, Jiangmen 529020, China; 2. School of Materials and Mineral Resources, Xi’an Univ. of Arch. &Tech., Xi’an 710055, China)

With the aid of the Patran software, a new finite model is established for the 1×6 straight strand and the IWRC straight wire rope and a finite element analysis and calculation is made using the Nastran. The calculation takes into account the variation of axial load with axial strain and load distribution in the situation where one end of the wire is fixed. Comparative finite element analysis result, theoretical calculation result and experimental result show that the errors in the three results are within the allowable range and verify the effectiveness of the finite element model.

steel wire rope; stress-strain; load distribution; FEA

1006-7302（2014）04-0067-05

O34；TD532

A

2014-07-09

五邑大学机械制造及其自动化重点学科项目（2021501）

王斌（1990—），男，江苏宜兴人，在读硕士生，研究方向为钢丝绳仿真、参数优化与数学模型研究；史天录，副教授，博士，硕士生导师，通信作者，研究方向为机电系统可靠性研究.