一个特殊谱任意符号模式矩阵

胡传峰，姬秀



一个特殊谱任意符号模式矩阵

胡传峰，姬秀

（长江大学 文理学院，湖北 荆州 434000）

符号模式矩阵；蕴含幂零；谱任意；极小谱任意；中心化子

符号模式矩阵主要研究其定性类中实矩阵所具有的仅与其元素符号结构有关而与其元素数值大小无关的组合性质，它起源于解决经济问题，除此以外，在化学、社会学及理论计算等科学领域也有着极其广泛的应用背景.

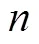
1 预备知识

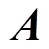
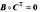
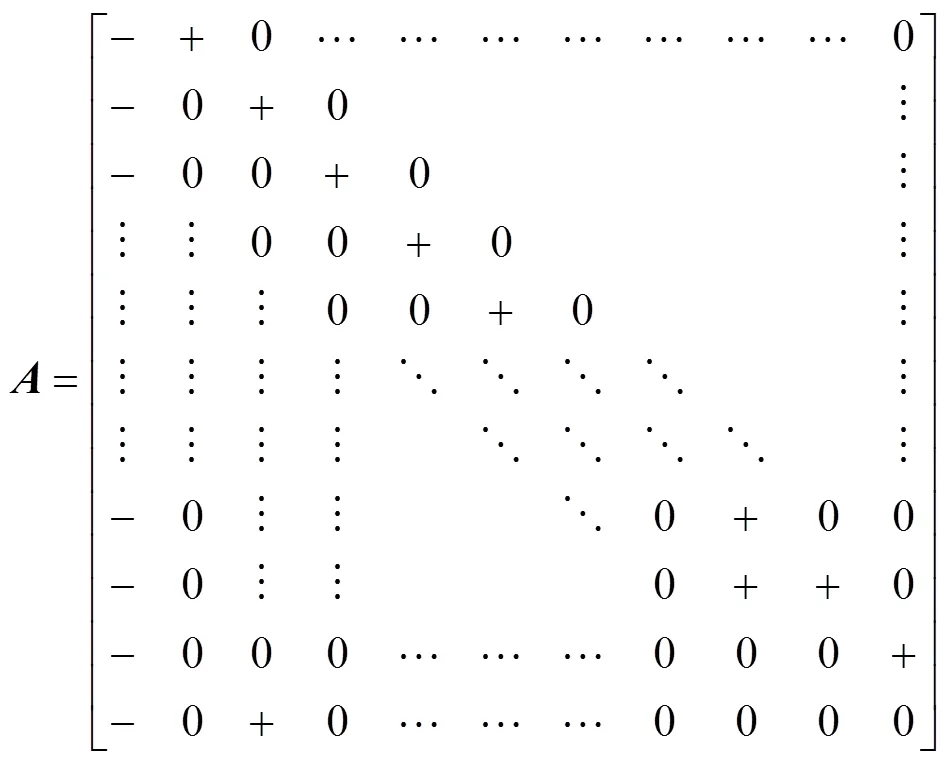
2 主要结果

2.1 幂零-雅可比方法

证明 1）

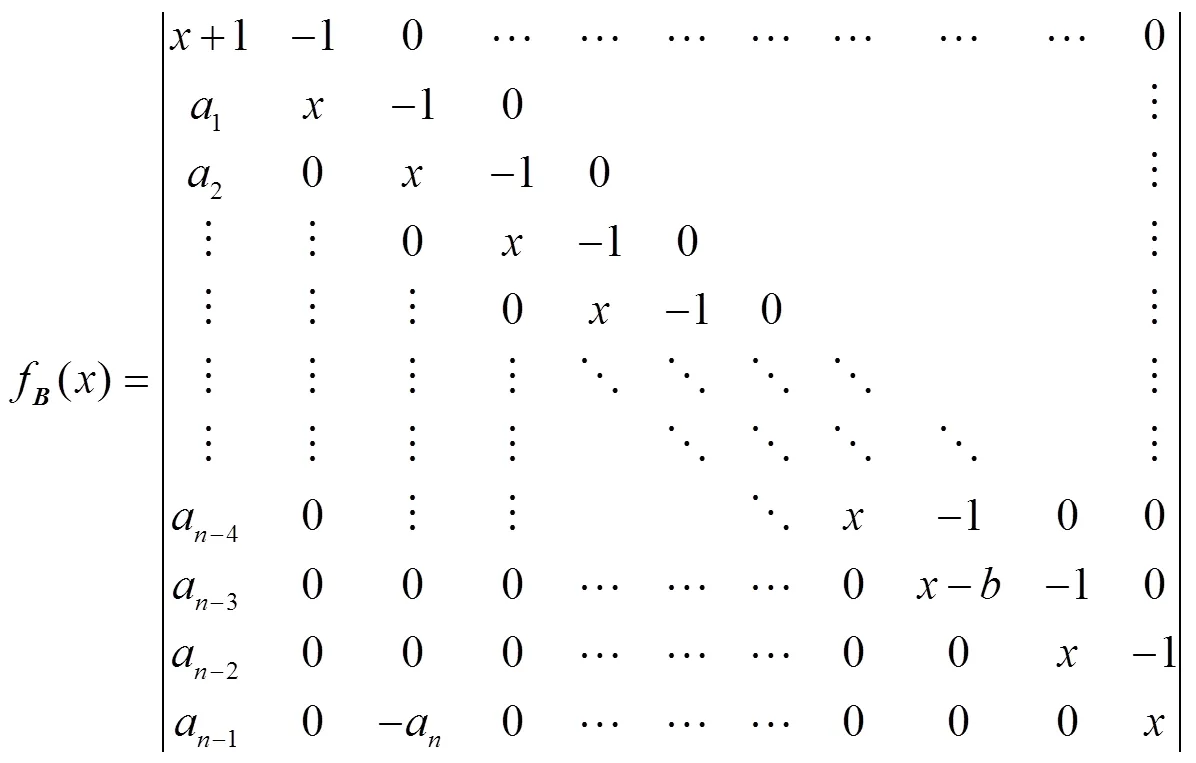
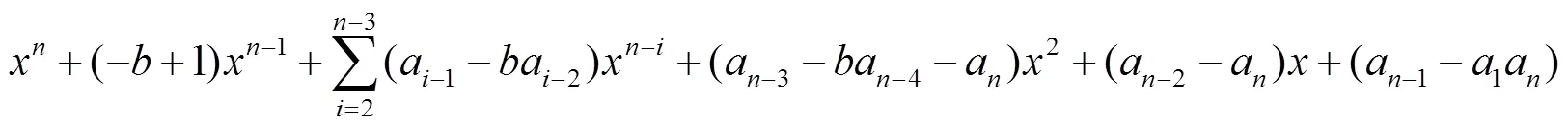
因此1）成立.

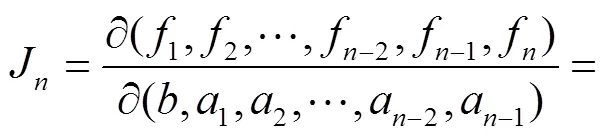
引理得证.

2.2 幂零-中心化子方法

由幂零-雅克比方法可知，实矩阵

定理得证.

[1] DREW J H, JOHNSON C R, OLESKY D D, et al. Spectrally arbitrary patterns [J]. Linear Algebra Application, 2000, 308: 121-137.

[2] BRITZ T, MCDONALD J J, OLESKY D D, et al. Minimal spectrally arbitrary sign patterns [J]. SIAM J Matrix Anal Appl, 2004, 26: 257-271.

[3] CAVERS M S, KIM I J, SHADER B L, et al. On determining minimal spectrally arbitrary patterns [J]. Elec J Linear Algebra, 2005, 13: 240-248.

[4] CAVERS M S, MEULEN K V N. Spectrally and inertially arbitrary sign patterns [J]. Linear Algebra Appl, 2005, 394: 53-72.

[5] MACGILLIVRAY G, TIFENBACH R M, DRIESSCHE van den P. Spectrally arbitrary star sign patterns [J]. Linear Algebra Appl, 2005, 400: 99-119.

[6] GARNETT C, SHADER B L. The Nilpotent-centralizer method for spectrally arbitrary sign patterns [J]. Linear Algebra Appl, 2013, 483(10): 3836-3850.

[责任编辑：熊玉涛]

A Special Spectrally Arbitrary Pattern Matrix

HUChuan-feng, JIXiu

(College of Arts and Science, Yangtze University, Jingzhou 434000, China)

sign pattern matrix; potentially Nilpotent; spectrally arbitrary sign patterns; minimal spectrally arbitrary sign patterns; centralizers

1006-7302（2014）04-0013-06

O157

A

2014-06-12

湖北省教育厅科学技术研究项目（B2014281）；长江大学文理学院科研基金资助项目（201303，201304）

胡传峰（1978—），男，河南信阳人，讲师，硕士，研究方向为组合数学与图论.