电控发动机故障诊断属性约简算法应用研究
2014-07-12谢春丽张东兴米志飞
谢春丽,张东兴,米志飞
(东北林业大学 交通学院,黑龙江 哈尔滨 150040)
电控发动机故障诊断属性约简算法应用研究
谢春丽,张东兴,米志飞
(东北林业大学 交通学院,黑龙江 哈尔滨 150040)
利用粗糙集理论中的区分矩阵属性约简算法对电控发动机的几种典型故障参数进行属性约简,为验证约简结果是否有利于下一步的故障诊断,采用较成熟的BP神经网络对其进行诊断验证,将约简结果作为网络的输入,待诊断故障作为网络的输出。通过学习训练结果表明:利用区分矩阵方法所获得的核约简不能作为故障诊断的特征参量,其导致网络不收敛,而其它3组约简可以用于区分现有故障。为获得最优的属性约简结果,利用二进制粒矩阵的方法进行了最优属性约简的证明。
粗糙集;属性约简;故障诊断;区分矩阵;二进制粒矩阵
粗糙集理论由波兰学者Pawlak在1982年提出[1]。此后,粗集理论引起了许多数学家、逻辑学家和计算机研究人员的兴趣,他们在粗集的理论和应用方面作了大量研究。Pawlak[2]系统全面地阐述了粗集理论,奠定了严密的数学基础,较好地总结了这一时期粗集理论与实践的研究成果,促进了该理论在各个领域的应用。属性约简是粗糙集理论的核心内容之一[3-4],将粗糙集理论的属性约简算法应用到故障诊断中[5-7],从而降低故障诊断特征参量的维数,提高后续故障诊断算法的运算速度,达到特征提取的目的。对于一般的基于粗糙集的属性约简算法寻求的目标是“最小”约简,而对于故障诊断中的属性约简则要求寻求“最优”约简,即获得能够最大限度判断故障类型,降低误诊的约简结果。
1 粗糙集理论的属性约简算法
基于粗糙集理论的属性约简算法非常多,人们对粗糙集的研究很大一部分是集中在研究属性约简这个范围内。下面简要介绍几种典型的目前研究较多的约简算法[8-9]。
1)基本算法 首先构造区矩阵,由区分矩阵产生区分函数,再对区分函数进行化简,得到区分函数的析取范式形式,析取范式中的每一项就是一个约简。
2)基于属性重要性的启发式算法 这个算法的基本思想是利用属性重要性作为启发式信息,将核属性作为初始属性集,在这个属性集中每次加入属性重要性最大的属性,直到剩下的属性的重要性都等于零为止,然后再检查这些属性是否可以删除,若可以则删除之,直到所有的属性都不能删除为止。这个算法能得到“最好”的约简或者是用户指定的“最小”约简。
3)动态约简 在某种意义上动态约简是给定决策表中最稳定的约简。该方法首先利用随机抽样从给定决策表中形成若干子表,然后计算所有子表的约简。如果某个约简在所有子表的约简中出现的频率大于给定的阈值,即在所有的子表中保持不变或近似保持不变的约简就是动态约简。动态约简能够有效地增强约简的抗噪音能力。
4)基于互信息的属性约简算法 基于互信息的属性约简算法是以bottom-up的方式来求相对约简的,它以决策表的相对核为起点,逐次选择最重要的属性添加到相对核中,直到条件满足。
2 基于区分矩阵的约简算法
这里以粗糙集的基本属性约简算法即区分矩阵法为基础来验证该算法在故障诊断中的应用。区分矩阵将复杂的信息系统容纳于一个矩阵中,却不影响原来信息系统中的潜在知识,因此大大提高了分析系统知识的能力,因此可以从区分矩阵入手对信息系统进行属性约简[10]。
定义1 设有信息系统S,a(x)是记录x在属性a上的值,Cij表示分辨矩阵中第i行,第j列的元素,Cij被定义为
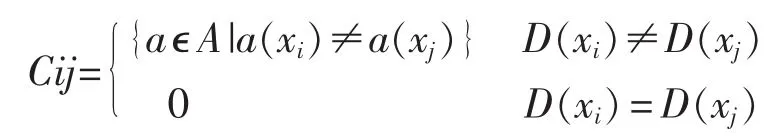
定义2(区分函数) 区分函数是从分辨矩阵中构造的。约简算法的方法是先求得Cij每个属性的析取,然后再求所有Cij的合取。分辨矩阵是一个对称n×n矩阵。在实际运用中,只列出它的上三角阵。
一个数据集的所有约简可以通过构造分辨矩阵并且化简由分辨矩阵导出的区分函数而得到,在使用吸收律化简区分函数成标准式后,所有的蕴含式包含的属性就是信息系统的所有约简集合。计算步骤如下[11]:
步骤1对数据库中的数据进行离散化处理。
步骤2 分别对xi和xj(1≤i<j≤n)进行比较,获取mij构造区分矩阵。
步骤3 对mij中各属性对应的变量进行析取运算,不同的mij采用合取运算。构造区分函数,将合取范式转换为析取范式。
步骤4根据所得析取范式获得决策表U的相对约简。
3 约简实例
以文献[12]中电控发动机的几种故障和相应的征兆为例,对该算法进行计算说明,各故障及相应的征兆如表1所示,假设故障数据经过离散化处理后的数据如表2所示,即决策表,根据决策表建立区分矩阵如表3所示。
根据建立的区分矩阵得决策表的区分函数:


得到该知识表达系统有 3个约简{x6,x10,x3,x7,x2,x11,x1},{x8,x10,x3,x7,x2,x11,x1},{x9,x10,x3,x7,x2,x11,x1},核是{x10,x3,x7,x2,x11,x1}。

表1 故障及相应参量含义

表2 离散化处理后数据

表3 区分矩阵
4 约简结果分析
为了验证约简结果是否可用于故障诊断的特征提取,采用较成熟的BP神经网络作为验证工具,将粗糙集理论所得到的3个约简及其核约简分别作为4个BP神经网络的输入,而待诊断的8种故障模式作为神经网络的输出。神经网络1将约简的核属性作为输入,结构为6-13-8;神经网络2将约简1的属性作为输入,结构为7-15-8;神经网络3将约简2作为输入,结构为7-15-8;神经网络4将约简3作为输入,结构为7-15-8。由于理想输出均相同,因此表4只给出了神经网络1和神经网络2的理想输入。
由于神经网络1的样本7和样本8的输入均相同,而输出却不同,导致了该网络学习训练不收敛,其余的神经网络经过学习训练后均收敛,只是循环计算的步数有所差别。各神经网络对样本1的实际输出、学习训练误差及训练计算循环步数如表5所示。
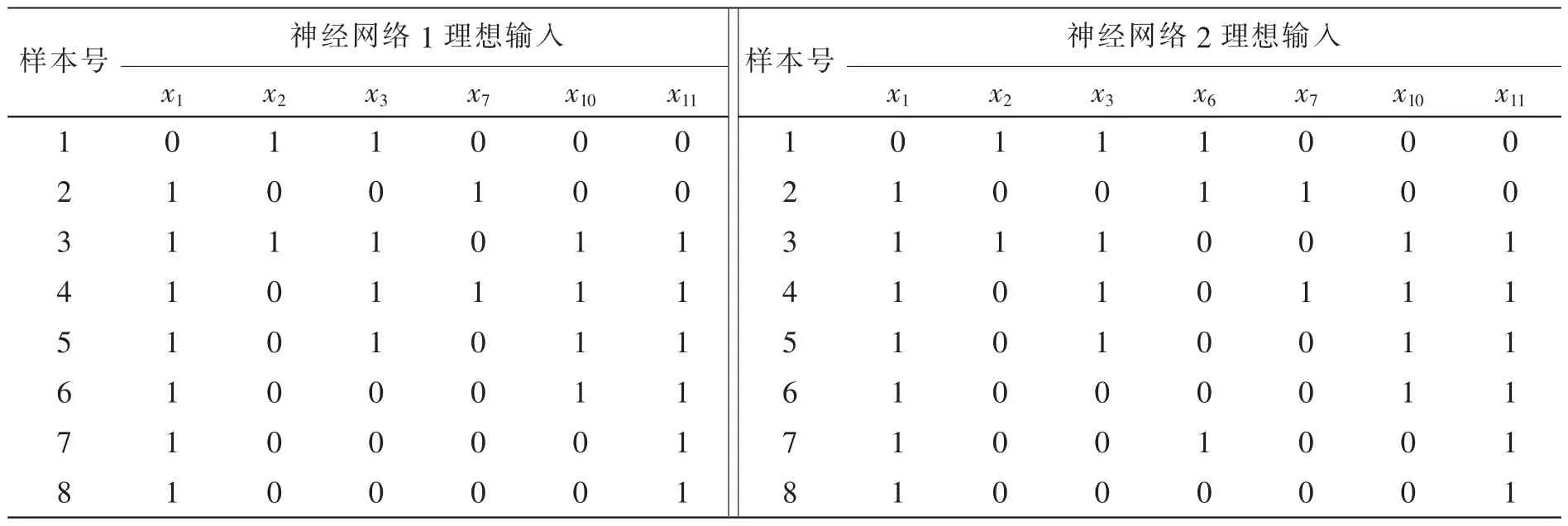
表4 神经网络1和2的理想输入

表5 神经网络的训练结果
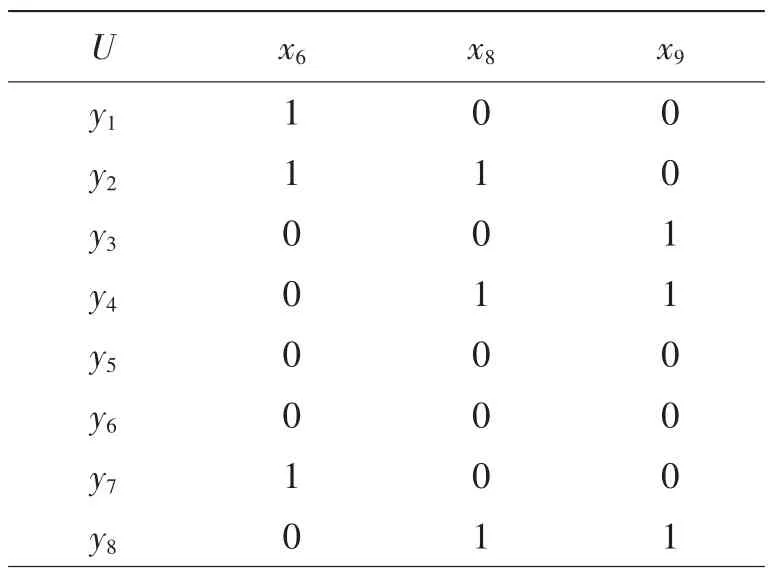
表6 去除其他属性后的决策表
5 最优属性约简结果的证明
通过对4个神经网络学习训练结果的分析来看,这里只使用粗糙集理论所获的核属性进行诊断是不可行的,造成网络不收敛,而使用粗糙集的3个约简进行诊断是可行的,通过训练结果的分析,使用3个约简作为神经网络的输入可以达到诊断这8种故障的目的。但这3种约简中到底哪一组约简结果是最优的,还是3种约简都是最优约简,利用二进制粒矩阵[13-16]的方法进行了证明。
从上面的3组约简结果来看除了核属性外,3组约简不同的是3个条件属性x6,x8,x9,只要计算出这3个条件属性的重要度即可确定最优约简,因此将其余属性均去掉得到决策表如表6所示。根据该决策表,当去掉属性x6后,条件属性C={x8,x9}划分论域U形成4个知识粒:

决策属性划分论域U仍为8种故障,因此形成的知识粒为 8个,即{(y1),(y2),(y3),(y4),(y5),(y6),(y7),(y8)}。
条件属性划分论域形成知识粒相应的二进制粒矩阵为
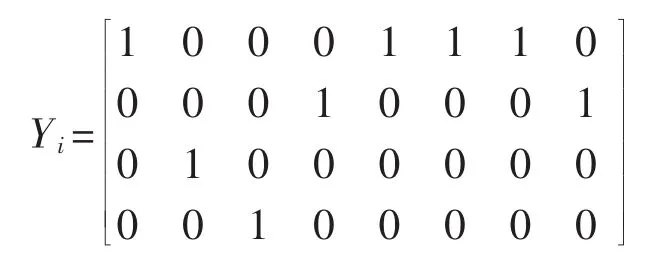
决策属性划分论域形成知识粒相应的二进制粒矩阵为

计算关系矩阵
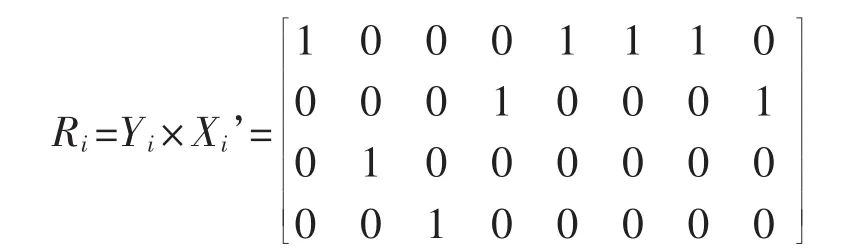
计算依赖度
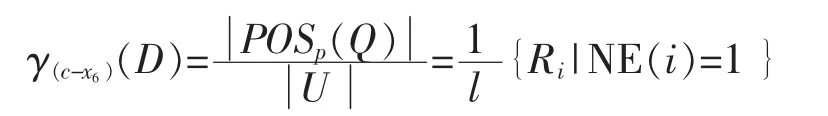
式中:NE(i)=1表示Ri中非零元素为1的个数。从关系矩阵中可以看出,行向量中只有一个非零元素的行有2个,即R中的第3行和第4行,而另外2行有多个非零元素,因此得
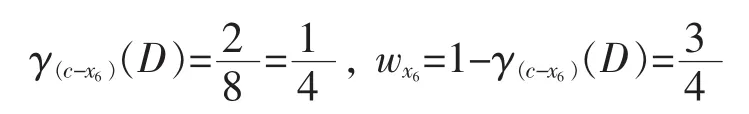
按照上述计算方法分别计算:
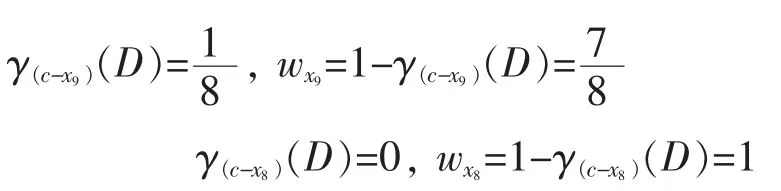
由此得x8的重要度最大,因此得到最优约简结果为{x8,x10,x3,x7,x2,x11,x1}。
6 结论
利用粗糙集理论的区分矩阵方法对给定的故障诊断决策表进行了属性约简,并给出了约简算法的详细计算过程,经约简计算后得到6个核属性及3组约简属性,利用神经网络对约简后的结果进行了验证,结果表明:6个核属性不能作为一个约简进行八种故障的识别,而3组约简结果均可识别目标故障。利用粗糙集理论的区分矩阵将原来的11个故障属性约简到7个故障属性,这大大简少了诊断算法的计算量,为各种智能诊断算法的应用及故障的快速识别奠定了基础。为了证明3组约简结果的优劣,寻求最优约简,提出了利用二进制粒矩阵的方法计算属性的重要度,通过计算依赖度的方法求得核属性之外的3个属性的重要度,在建立决策表时,只考虑待求3个属性而将其他属性略去,这样大大简化了计算量,能够快速寻求最优约简结果,该方法可以进一步应用于其他属性约简结果的寻优计算中。
[1]王庆东.基于粗糙集的数据挖掘方法研究 [D].杭州:浙江大学,2005.
[2]Zdzisław Pawlak,Andrzej Skowron.Rudiments of rough sets[J].Information Sciences,2007,177(1):3-27.
[3]Yuhua Qian,Jiye Liang,Witold Pedrycz,Chuangyin Dang.An efficient accelerator for attribute reduction from incomplete data in rough set framework[J]. Pattern Recognition.2011,44(8):1658-1670.
[4]甄宇峰.基于粗糙集的知识约简算法研究及应用[D].镇江:江苏大学,2010.
[5]N.R.Sakthivel,V.Sugumaran,Binoy.B.Nair.Comparison of decision tree-fuzzy and rough set-fuzzy methods for fault categorization of mono-block centrifugal pump[J]. Mechanical Systems and Signal Processing,2010,24(6):1887-1906.
[6]Bing Li,Peng-yuan Liu,Ren-xi Hu,Shuang-shan Mi, Jian-ping Fu.Fuzzy lattice classifier and its application to bearing fault diagnosis[J].Applied Soft Computing, 2012,12(6):1708-1719.
[7]Karim Salahshoor,Mojtaba Kordestani,Majid S.Khoshro. Fault detection and diagnosis of an industrial steam turbine using fusion of SVM (support vector machine)and ANFIS (adaptive neuro-fuzzy inference system)classifiers[J].Energy,2010,35(12):5472-5482.
[8]邓大勇.基于粗糙集的数据约简及粗糙集扩展模型的研究[D].北京:北京交通大学,2007.
[9]K.Thangavel,A.Pethalakshmi.Dimensionality reduction based on rough set theory:A review[J].Applied Soft Computing,2009,9(1):1-12.
[10]高淑芝,高宪文,王介生,等.基于改进差别矩阵属性约简的聚合釜粗糙集-神经网络故障诊断[J].化工学报,2011,62(3):759-765.
[11]张楠.基于Rough Set理论的约简算法的研究[D].贵阳:贵州大学,2007.
[12]李明钊.基于神经网络的电控汽油发动机的智能故障诊断研究[D].昆明:昆明理工大学,2008.
[13]谢珺.二进制粒神经网络研究及其在故障诊断中的应用[D].太原:太原理工大学,2009.
[14]Scott Dick,Andrew Tappenden,Curtis Badke,Olufemi Olarewaju.A granular neural network:Performance analysis and application to re-granulation [J]. International Journal of Approximate Reasoning,2013(54):1149-1167.
[15]陈泽华.粒计算及人工选择算法理论研究[D].太原:太原理工大学,2007.
[16]Vassilis G.Kaburlasos,S.E.Papadakis.A granular extension of the fuzzy-ARTMAP(FAM)neural classifier based on fuzzy lattice reasoning(FLR)[J].Neurocomputing,2009(72):2067-2078.
Application Research on Attribute Reduction Algorithm for Fault Diagnosis of Electronic-controlled Engine
Xie Chunli,Zhang Dongxing,Mi Zhifei
(Traffic College,Northeast Forestry University,Harbin 150040,China)
Several typical faults parameters of electronic-controlled engine were taken as an example to do attribute reduction using discernible matrix of rough set theory.In order to validate reduction results whether it helps the next fault diagnosis,the relatively mature BP neural network was chosen to test and verify.The reduction results are as the inputs of BP neural network,and the typical faults are as outputs.The training results show that the
core reduction using the discernible matrix method cannot be used as the characteristic parameters of fault diagnosis,it does not cause network convergence,and the other three groups of reduction can be used to distinguish the existing faults.In order to get the best attribute reduction,the optimal attribute reduction was proved by using Bit Granular Matrix.
rough set;attribute reduction;fault diagnosis;discernible matrix;Bit Granular Matrix
TP18
A
1008-5483(2014)01-0054-05
2014-01-13
中央高校基本科研业务费专项资金项目资助(DL13CB14)
谢春丽(1978-),女,吉林镇赉人,副教授,主要从事故障诊断方面的研究。
10.3969/j.issn.1008-5483.2014.01.0014
