基于6σ鲁棒性分析的薄壁结构弯曲吸能特性优化设计

张伟，谷先广，马尧，王新树

（合肥工业大学 机械与汽车工业学院，安徽 合肥 230009）

基于6σ鲁棒性分析的薄壁结构弯曲吸能特性优化设计

张伟，谷先广，马尧，王新树

（合肥工业大学 机械与汽车工业学院，安徽 合肥 230009）

结合试验设计、Kriging近似建模技术、Monte Carlo模拟技术，对多种截面薄壁结构进行了确定性优化，并构造了基于6σ鲁棒性分析的优化方法。研究结果表明：实现了对薄壁结构的抗弯吸能特性的优化，并提高了产品质量的可靠性。

6σ鲁棒性优化；Kriging近似模型；薄壁结构；弯曲吸能特性；有限元分析

0 前言

随着汽车、航空、航天、以及建筑等行业的快速发展，具有质量轻、强度高、低耗能且易于实现精确制造等优点的薄壁构件被广泛使用［1］。作为一种缓冲吸能结构，薄壁构件在汽车行业中应用普遍并被进行了大量的研究［2］。在轴向冲击下，薄壁构件呈现出平稳承载及高效吸能的特性，但实际的汽车碰撞实验表明，汽车中90%以上部件均存在着弯曲失效［3］。在车辆发生侧面碰撞时，吸能结构主要发生弯曲压溃变形［4］，因此，对薄壁结构的弯曲吸能特性进行研究有着十分重要的意义。

传统的优化设计由于忽略不确定因素的影响，如材料特性、载荷状况、生产精度和产品的实际应用环境等会存在波动，可能导致设计最优目标超出约束界限而使设计失效,使质量水平和合格率降低［5］。另外，目前对薄壁结构的相关研究主要集中在轴向冲击吸能特性方面，对薄壁结构的弯曲碰撞吸能方面的研究较少，将优化模型中设计变量的不确定性予以考虑的研究少之又少。

为了解决上述问题，结合Kriging近似建模技术、均匀拉丁方试验设计和可靠性设计理念，以薄壁矩形结构为例，对其弯曲吸能特性进行了鲁棒性优化设计，优化结果提高了该结构的弯曲吸能特性，且相对于确定性最优解，优化结果的可靠性得到了较大提升。除此之外，还比较了3个不同截面形状的薄壁结构，并通过优化分析从中选取了弯曲吸能特性最优的截面，使薄壁结构能最大化地吸收冲击能量以实现结构的防护性。

1 有限元模型的建立与验证

1.1 有限元模型的建立

参照文献［6］中的实验模型建立了有限元模型，矩形截面薄壁梁弯曲碰撞示意图如图1所示，整个结构的长度为550mm，横截面为矩形薄壁形状，其长度、宽度均为55mm，厚度为2mm，冲击质量块结构以4.4m·s-1的初速度碰撞薄壁结构。

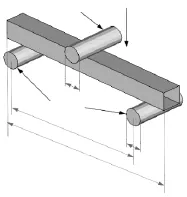
图1 弯曲碰撞模型示意图

采用显式有限元计算软件LS-DYNA来模拟弯曲变形的整个碰撞过程。薄壁结构材料为铝合金6060，结构采用Belytschko-Tsay单点积分壳单元通过Hypermesh软件进行有限元建模，厚度方向有5个积分点，材料模型为24号材料，材料真实应力应变曲线如图2所示，相关材料参数杨氏模量E为70GPa，密度ρ为2.7×103kg·m-3，泊松比v为0.3。支撑块和冲击质量块均采用体单元进行建模，材料模型为20号刚性材料。

考虑到实际应用中薄壁结构形式较多，针对3种薄壁截面进行了优化分析，具体截面形状如图3所示。图3中截面厚度为t；截面高度为w；宽度均为55mm；高宽比为r。

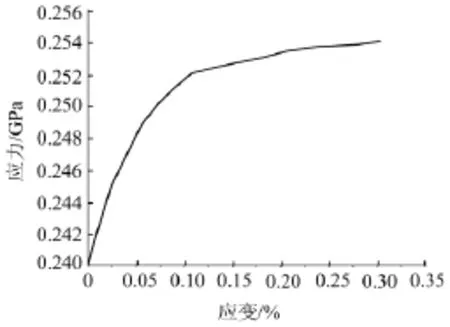
图2 材料真实应力应变曲线

图3 截面形式

1.2 有限元模型的验证

通过对比该有限元模型仿真所得曲线与文献［6］中的试验所得曲线（图 4），图 4中横坐标“位移”指质量块质心处冲击位移；纵坐标“冲击载荷”指薄壁结构碰撞接触载荷，即二者碰撞接触面反作用力。可知，仿真曲线较好地贴合了试验曲线，且在曲线整体趋势一致，说明有限元模型可信度较高，在保证相关材料参数和控制参数不变的情况下，通过试验设计点来进行仿真分析所得到的计算结果准确可靠。

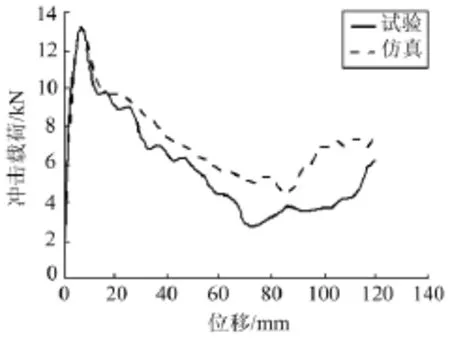
图4 试验曲线与仿真曲线对比

2 近似模型的建立与验证

2.1 试验设计

优化拉丁方试验设计是一种约束随机的生成均匀样本点的试验设计和采样方法，该方法效率高、采样均衡性好［7］。笔者采用优化拉丁方试验设计方法，共选取了36个样本点，并进行有限元仿真计算，得出的设计变量及试验结果如表1所示（由于篇幅原因，仅列出截面一试验列表）。其中设计变量高宽比r的随机取值范围为0.7～1.3，厚度t的取值范围为1.5～2.5mm。

表1 设计变量及响应值试验列表

2.2 Kriging近似模型的建立

确定性优化和可靠性优化均以近似模型为基础，采用36个样本点数据分别构建了截面1、截面2、截面3的Kriging近似模型。图5为与3个截面相对应的近似模型的SEA响应面图。

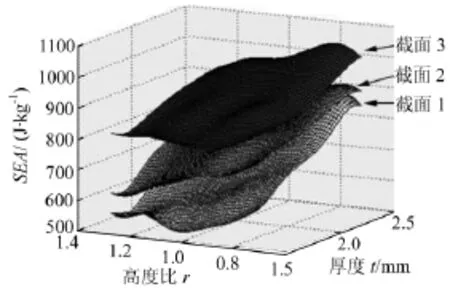
图5 近似模型响应面图（比吸能）

2.3 Kriging近似模型的验证

为了检验Kriging近似模型的拟合精度，选取任意3个试验点进行比较［8］，结果如表2所示。从表2可以明显看出,采用近似模型计算得到的结果与直接应用LS-dyna软件计算得到的结果非常接近，相比误差均在2%以内，表明Kriging近似模型精度高。因此，采用Kriging近似模型来代替直接的有限元仿真计算是可行的。

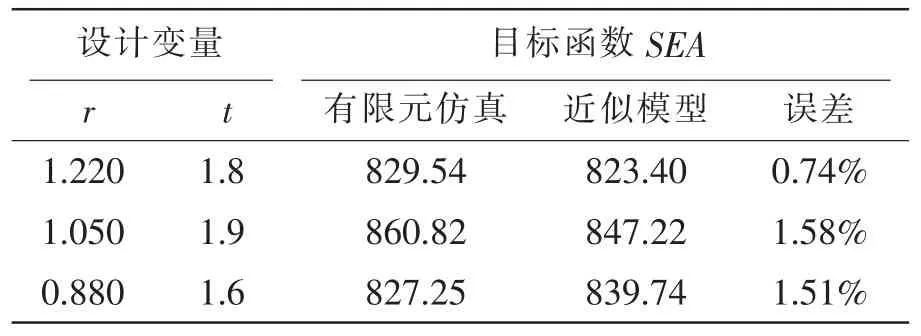
表2 Kriging近似模型采样点及其预测误差

3 弯曲吸能优化设计

3.1 问题描述

将对具有不同截面形状的薄壁结构尺寸进行优化，找寻影响其抗弯吸能性能的最佳尺寸组合，使该薄壁结构能够在满足轻量化和安全性的条件下具有最大弯曲吸能特性。

对于3种截面的薄壁构件对其抗弯性的影响因素，选取该薄壁构件的厚度、截面的高度相对于宽度的比值（即高宽比）为设计变量；同时考虑薄壁件在弯曲过程中的安全和吸能要求，将峰值载荷和平均载荷分别限制在18kN以下和11kN以上；在保证峰值载荷不大于限制要求的情况下，薄壁构件的比吸能越大，则表明薄壁构件的抗弯吸能性越好，这样既能保证吸能效果，又能满足轻量化的要求［9］。因此，定义薄壁构件的比吸能的最大值作为优化设计的目标函数。

3.2 确定性优化

根据建立的各响应的Kriging近似模型，构建确定性优化数学模型如下：

式中：SEA为结构弯曲比吸能，J·kg-1；Pavr为平均载荷，kN；Pmax为峰值载荷，kN；r为薄壁截面高宽比；t为薄壁厚度值，mm。

由确定性优化结果对比表3可知，确定性优化使得该结构比吸能由690.8 J·kg-1分别上升至截面 1、截面 2、截面 3所对应的 873.8 J·kg-1、893.0J·kg-1、815.3J·kg-1。经过确定性优化后，该结构的弯曲碰撞比吸能有明显提高，显而易见，截面2在相同约束条件下优化出来的比吸能最大，结果最优。

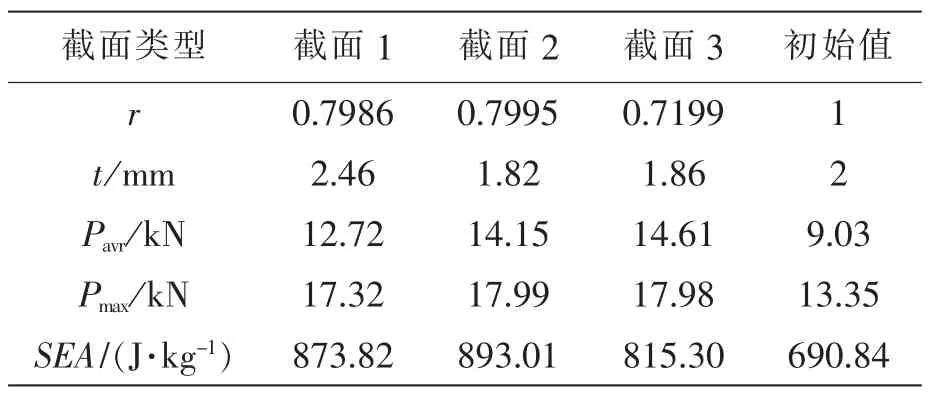
表3 确定性优化结果对比

然而，截面 2的优化结果中峰值载荷为17.9918kN，接近约束边界18kN，考虑加工工艺因素，在实际加工过程中，薄壁部件的宽度和壁厚均具有一定的不确定性，可能会造成产品不满足质量目标的情况［10］。故需对截面2的优化结果进行进一步的6σ可靠性质量分析。

3.3 基于蒙特卡罗分析技术的鲁棒性优化

鲁棒性是指不确定因素影响下响应变化的稳定性，鲁棒性优化设计主要是控制和减少目标函数响应的波动，降低目标函数值在设计点上的敏感性，即减小目标函数的响应均方差，实现均方差最小化和均值达到设计目标的目的［11］。在可靠性分析时采用蒙特卡罗（Monte Carlo）模拟技术，也称统计模拟方法，它是一种以概率统计理论为指导的数值计算方法，可以用来考察优化解在不确定性环境下的鲁棒性。

为了研究设计参数波动对约束和目标的影响，假设设计变量服从于正态分布，设计变量高宽比和厚度的变异系数均为0.01。该可靠性优化问题的数学模型为

式中：SEA为结构弯曲比吸能，J·kg-1；Pavr为平均载荷，kN；Pmax为峰值载荷，kN；r为薄壁截面高宽比；t为薄壁厚度值，mm。

表4 优化设计结果对比

对确定性优化数学模型和可靠性优化数学模型进行优化可得表4所示的优化结果。由表4可知，确定性优化过程使得该薄壁结构的比吸能由690.8J·kg-1上升至893.0J·kg-1。然而，当设计变量波动时，优化目标SEA的均方差为4.06，且弯曲碰撞峰值载荷 Pmax的 σ水平为 2.88， 可靠度为99.6%，约束的质量水平较低，可靠性优化使得优化目标上升至875.9J·kg-1，尽管这一结果比确定性最优解差，但是此时优化目标 SEA的均方差为0.144，方差值较确定性优化结果有所减小，且此时约束函数Pmax的σ水平提高至8，可靠度均提高至100%，其质量水平得到了大幅度的提高。确定性优化和可靠性优化结果的约束质量概率密度分布图如图6所示。

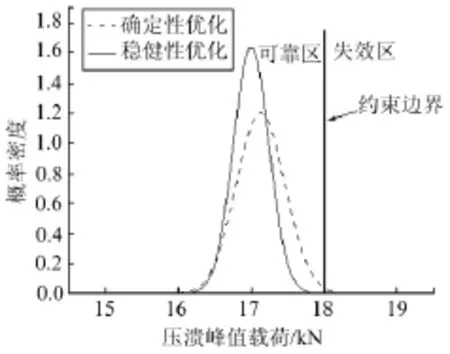
图6 确定性优化与可靠性优化约束质量概率密度分布

3.4 优化方案的验证

初始方案、确定性优化结果和可靠性优化结果的比吸能随时间的变化曲线如图7所示。由图7可知，确定性优化和可靠性优化都使得比吸能SEA相对于初始方案得到了一定的提升，虽然可靠性优化结果与确定性优化结果相比比吸能值略小，然而，相比较确定性优化结果，可靠性优化结果使得约束Pmax条件远离约束边界。

除此之外，该算例也说明可靠性优化设计方法与近似模型建模技术相结合对于薄壁结构的抗弯吸能优化问题具有很强的工程实用性。

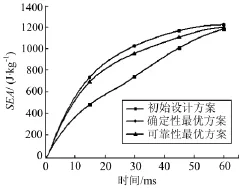
图7 优化前后比吸能随时间变化曲线

4 结论

通过对3种不同截面薄壁构件的确定性优化设计和可靠性优化设计可以得到以下结论：

1）使用Kriging近似模型替代有限元仿真计算是可行的，并能得到准确的计算结果，可以提高优化效率；

2）在近似模型的基础上，通过对3种截面薄壁构件的确定性优化分析，确定了3种截面中的抗弯吸能性能最优截面；

3）结合试验设计、近似建模技术、Monte Carlo可靠性分析及可靠性优化设计理念，对薄壁构件进行了可靠性优化设计，一方面改善了结构的抗弯吸能特性，另一方面也提高了产品质量的可靠性。该方法可推广应用到汽车工业中,为汽车结构的零部件或整车的抗弯吸能优化提供新的解决途径。

［1］张丰收，李兮蒈，金建利，等.薄壁矩形管弯曲成形起皱变形的研究综述［J］.现代制造工程，2012（11）：131-134.

［2］蒋致禹，顾敏童，赵永生，等.一种薄壁吸能结构的设计优化［J］.振动与冲击，2010，29（2）：111-116.

［3］郭刘伟.泡沫铝夹芯双管结构的力学行为研究［D］.合肥：中国科学技术大学，2010.

［4］宫保贵，王青春，王国权，等.泡沫铝部分填充薄壁梁弯曲吸能特性研究［J］.计算机真，2009，26（12）：230-234.

［5］孙光永，李光耀，王建华，等.可靠性优化设计在汽车构件耐撞性中的应用 ［J］.计算机辅助设计与图形学学报，2007，19（10）：1308-1314.

［6］H.R.Zarei，M.Kroger.Bending behavior of empty and foam -filled beams: Structural optimization ［J］. Internation-al Journal of Impact Engineering，2008，35：521-529.

［7］陈潇凯，李邦国，林逸，等.改进响应面法在汽车正面抗撞性优化中的应用 ［J］.北京理工大学学报，2009，29（12）：1076-1079，1084.

［8］龚旭，谷正气，李振磊，等.基于近似模型的集装箱半挂车导流罩的形状优化［J］.汽车工程，2011，33（1）：38-42.

［9］侯淑娟.薄壁构件的抗撞性优化设计［D］.长沙：湖南大学，2007.

［10］孙光永,李光耀,张勇，等.基于鲁棒性的概率优化设计在薄壁构件耐撞性中的应用 ［J］.中国机械工程，2007，18（4）：479-483.

［11］张佳洪，李光耀，高晖，等.鲁棒性概率优化在乘员约束系统设计中的应用 ［J］.中国机械工程，2010（5）：505-509.

Optimum Design on Bending Energy Absorbing Ability of Thinwalled Structure Based on 6σ Robustness Analysis

Zhang Wei,Gu Xianguang,Ma Yao,Wang Xinshu
（School of Mechanical and Automotive Engineering,Hefei University of Technology,Hefei 230009,China）

The thin-walled structure of different sections was optimized through the applications of DOE and Kriging approximate modeling and Monte Carlo simulation techniques,and an optimization method was constructed based on 6σ robustness analysis.The results show that the optimization in bending energy absorbing ability is realized and the robustness of thin-walled structure’s quality is improved.

6σ-based robustness optimization;Kriging approximate model;thin-walled structure; bending energy absorbing ability;finite element analysis

U461

A

1008－5483（2014）01－0025－05

2014-02-12

张伟（1989-），男，安徽六安人，硕士生，从事车辆现代设计理论与方法方面的研究。

10.3969/j.issn.1008-5483.2014.01.007