高过载条件下电雷管桥丝损伤的模型分析
2014-07-12孙晓霞沈瑞琪吴立志
刘 卫,孙晓霞,沈瑞琪,吴立志
高过载条件下电雷管桥丝损伤的模型分析
刘 卫,孙晓霞,沈瑞琪,吴立志
(南京理工大学化工学院,江苏 南京,210094)
基于解析几何学的基本原理,建立双脚线电雷管的桥丝在横向过载时受拉损伤的计算模型,获得桥丝拉伸率、临界初始角度和电阻值的变化规律。结果表明:桥丝拉伸率、临界初始角度及电阻变化率均随电极塞横截面椭圆度的增加而增加;当桥丝的初始角度小于45°,桥丝未受拉伸作用,电雷管的最佳放置方式是桥丝平行于电雷管的运动方向。这与ANSYS/LS-DYNA数值仿真结果十分吻合,所建立的模型可以较准确地描述横向过载时桥丝的损伤特性。
电雷管;桥丝;高过载;空气炮;横向损伤
作为弹药的首发器件和装置,火工品在武器系统中起着至关重要的作用。在弹体斜侵彻[1-3]以及子母弹爆炸抛撒[4-5]等高过载环境中,弹体经常会经历高温、高压及大变形的严酷环境,同时受到来自于横向的惯性力和应力波作用。在这种条件下,必须保证火工品的可靠性,使其免于意外作用。李创新[6]采用空气炮过载试验装置来研究桥丝式电雷管的受载损伤过程,结果表明,在横向过载条件下,电雷管的损伤程度要远大于在轴向过载时的损伤程度,主要表现为桥丝断裂和意外发火。分析认为,在横向过载时,电雷管受自身惯性和应力波双重作用时,其横截面由圆形变成椭圆形[7]。此时,若桥丝放置方向垂直于电雷管的运动方向,则桥丝会因受到拉伸而导致阻值变大,甚至断裂。
本文利用空气炮试验装置对桥丝式双脚线电雷管进行横向加载,获得桥丝的损伤现象。然后基于解析几何学的基本原理,建立了横向过载条件下桥丝式双脚线电雷管的桥丝受拉损伤的计算模型,并获得桥丝尺寸和电阻值的变化规律,为火工品的抗横向过载加固和结构设计提供理论支撑。
1 电雷管的横向过载试验
1.1 试验方法
空气炮试验系统主要由支架、发射炮管、子弹、气动控制系统、测速系统和回收靶室等组成,如图1所示。由于弹体尺寸的限制,无法使用弹载加速度传感器获得弹体的着靶加速度,因此,过载试验中,只能采用铜柱测压法得到弹体的受载情况。所用假品桥丝式双脚线电雷管的尺寸为Φ5.10mm×10mm,采用滑石粉代替电雷管装药。电雷管在子弹内的安装方式如图2所示,试验所采用子弹的尺寸为Φ36.5mm ×97mm,重量约为625g。

图1 空气炮试验装置的原理示意图
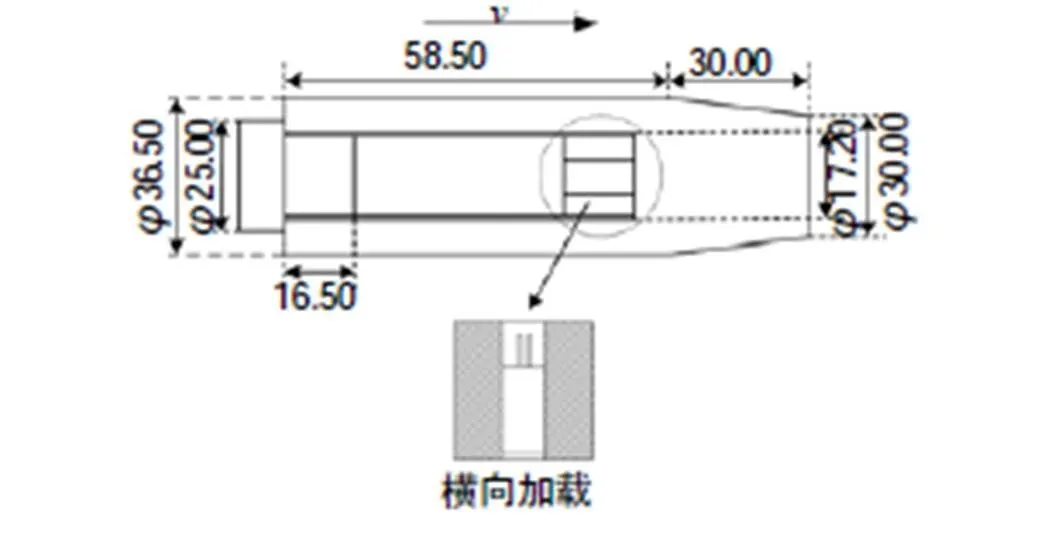
图2 横向过载时电雷管的安装方法
子弹经过高压气体的瞬间推动,沿着Φ37mm直径的炮管向前运动,通过遮挡式双光路测试系统的测速后,撞击到铅直放置于回收室内的钢板,从而实现对电雷管的高加速度加载试验。
1.2 结果与讨论
分别在6×104g、8×104g、10×104g、12×104g的条件下对桥丝式双脚线电雷管进行加载试验,每个条件下进行3发平行试验。过载前、后分别测量电雷管桥丝的电阻,并计算电阻平均变化率,结果如表1所示。研究发现,随着过载加速度的增加,过载前、后电雷管桥丝电阻变化无显著规律。但是,通过统计发现,约有33%电雷管的桥丝发生断裂。解剖桥丝断裂的电雷管,在显微镜下观察,结果如图3所示。
表1 电雷管桥丝的电阻变化率

Tab.1 Resistance change ratios of the bridge wire
注:*有1发电雷管桥丝断裂;**有2发电雷管的桥丝断裂

图3 电雷管的桥丝断裂形貌
研究发现,桥丝损伤主要受到应力波的作用和电极塞变形对桥丝形成的拉伸作用的双重影响,其中后者是主要因素[6-7]。
2 桥丝损伤计算模型
2.1 电极塞横截面变形分析
高过载条件下,横向过载时,电雷管的电极塞发生变形,其截面由圆形变成近似椭圆形。在该过程中,以电极塞的中心为原点,两焊点之间距离为直径的圆弧也必然变成椭圆形,如图4所示。
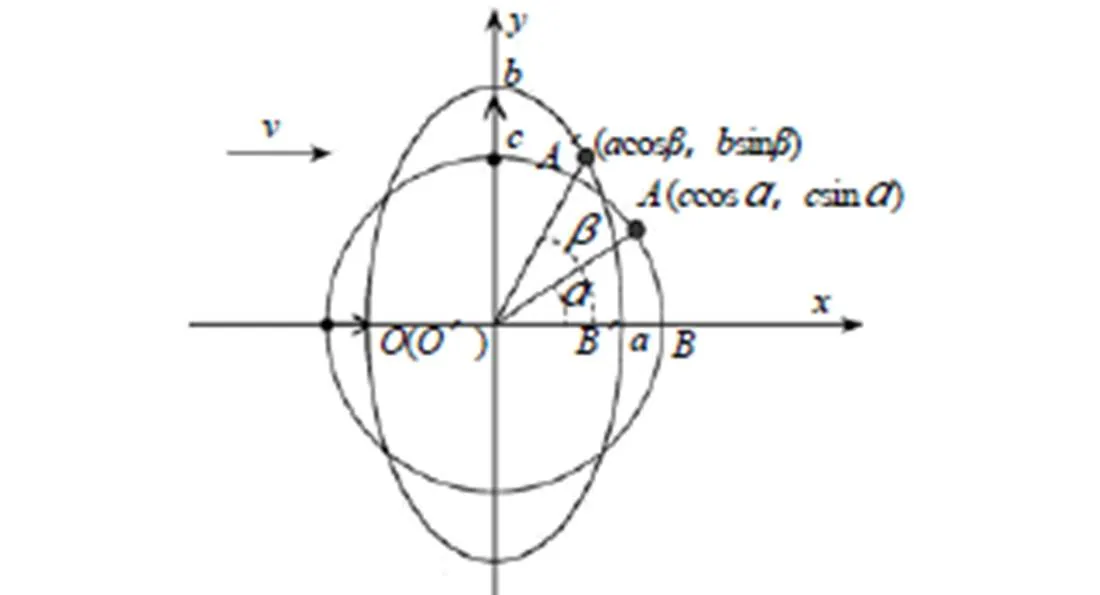
图4 电极塞横截面变形示意图
加载前,桥丝的焊点在直径为2c的圆O上A点的位置,A点的坐标可以表示为 (cos,sin)。过载后,焊点运动到椭圆O’上的A’点。若椭圆的短半轴和长半轴分别为和,则A’点的坐标为(cos,sin)。其中,、均为坐标点与轴的夹角,表征了过载前电雷管的放置状态。当=0时,桥丝放置方向与运动方向平行,当=90°时,表示桥丝放置方向与运动方向垂直。考虑到结构的对称性,计算时限定值在0~90°的区间。
根据解析几何的基本原理,过载前焊点所在圆截面的方程或参数表达式为:
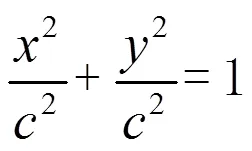
过载后,焊点所在椭圆截面的表达式为:

2.2 桥丝的长度变化
过载前后,桥丝的长度变化可以用拉伸率表示:
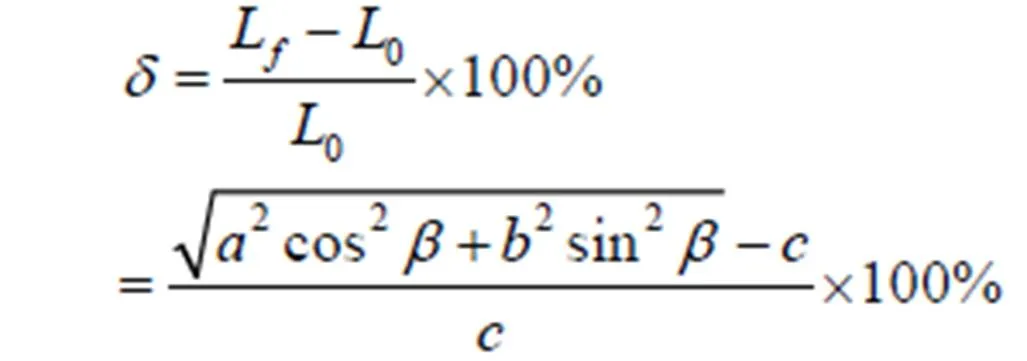
(3)

椭圆度的大小表征了电极塞的损伤程度。
通常情况下,由于电极塞变形较小,可以忽略电极塞的周长变化,即AB的弧长等于A’B’的弧长,则必然有:
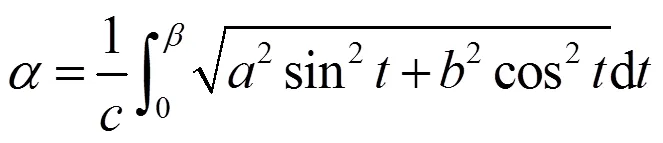
根据式(3)和式(5),将作为中间量,即可得到与之间的关系。
2.3 桥丝的阻值变化
桥丝电阻的计算公式可以表示为:
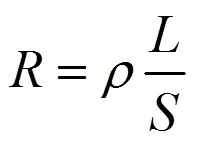
式(6)中:为桥丝材料的电阻系数或电阻率,、分别为桥丝的长度和横截面积。
在加载过程中,假设桥丝均匀受拉,则过载后桥丝各处的横截面积相同。若过载前后桥丝的体积不变,则有:
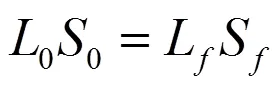
式(7)中:0和S分别为桥丝受载前、后的横截面积。忽略高过载过程中桥丝的温度变化,则电阻率为恒值。根据式(6)和(7),计算受载之后桥丝的电阻变化率,化简之后为:

式(8)中:0和R分别为过载前后桥丝的电阻值。
3 模型验证
由于试验过程中很难获得电极塞的损伤状况,故只能将模型计算结果与数值仿真结果进行比较,以验证计算模型的正确性。基于空气炮过载试验平台,采用LS-DYNA非线性显式动力学仿真软件模拟计算电雷管的过载损伤情况。计算时,弹体以80m/s和40m/s的速度撞击钢性靶板,得到子弹的过载加速度曲线如图5所示。
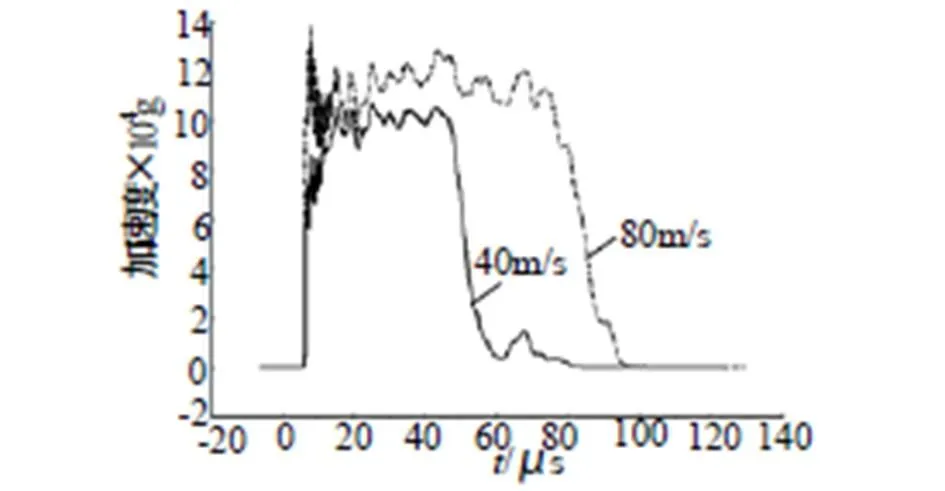
图5 子弹的过载加速度曲线
从图5可以看出,当弹体的速度分别为80m/s和40m/s,过载加速度的平均值分别为12×104g和10× 104g,脉宽分别约为86μs和52μs。
通过后处理过程,得到过载前后焊点所在圆弧上的节点坐标,并计算每个节点的初始角度和最终角度。根据式(3)和式(5)得到桥丝拉伸率与初始角度之间的关系。同时,测量过载后电极塞椭圆形截面的短轴和长轴,并根据式(3)和(5)从理论上计算桥丝拉伸率与初始角度。比较模型与LS-DYNA计算结果,如图6所示。
从图6可以看出,在撞击速度为40m/s和80m/s的情况下,模型计算结果与LS-DYNA数值仿真数据吻合程度较好,这表明,基于解析几何原理建立的半经验公式具有较好的可靠性。
在撞击速度为80m/s时,根据模型计算电极塞横截面外轮廓的形状,并将结果与数值仿真结果进行比较,结果如图7所示。
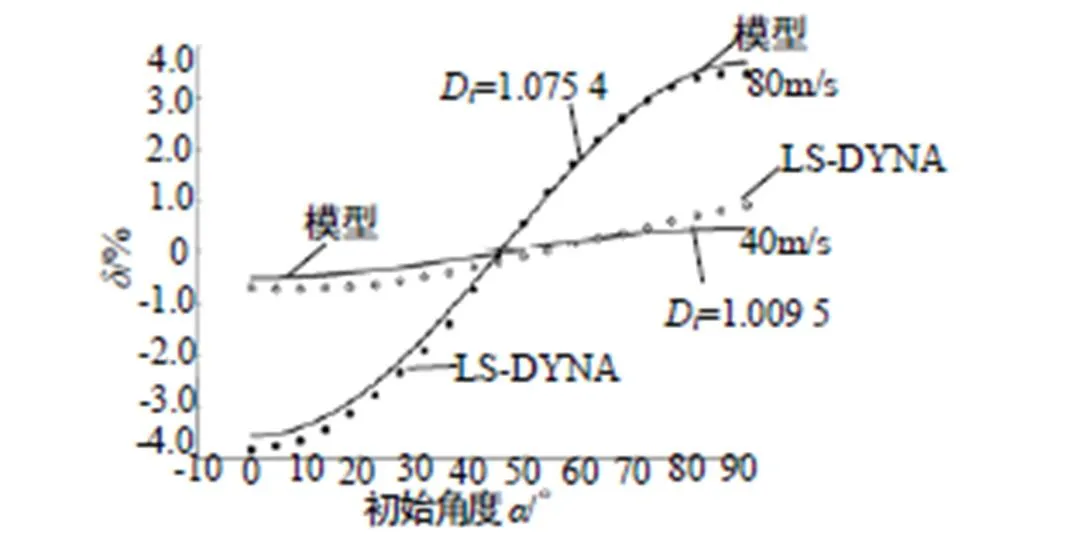
图6 桥丝拉伸率与桥丝初始角度的关系
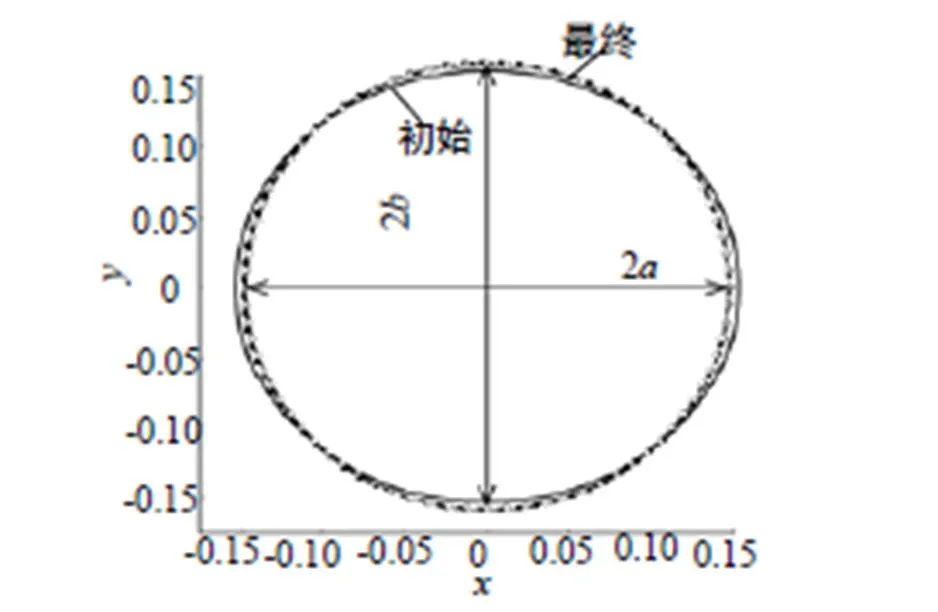
图7 电极塞截面的形状
从图7可以看出,加载后,电极塞横截面由初始的圆形变成了椭圆形,经计算,电极塞的椭圆度为1.075 4。另外,模型计算结果与数值仿真结果十分吻合。
4 桥丝损伤变化规律
4.1 拉伸率与电极塞横截面椭圆度之间的关系
当桥丝的初始角度一定时,桥丝的拉伸率随电极塞横截面椭圆度的变化情况如图8所示。
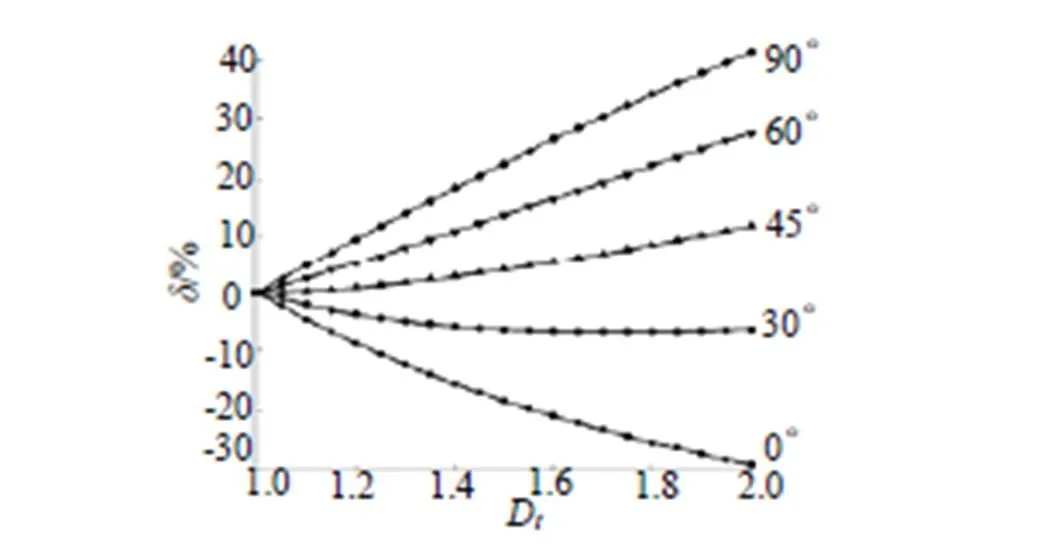
图8 桥丝拉伸率与电极塞椭圆度之间的关系
图8的结果表明,当桥丝的初始角度为0时,桥丝的拉伸率小于0,即在此角度下,桥丝不被拉伸,而会折弯。“折弯”是指由于焊点之间距离的减小而使桥丝发生弯曲。随着椭圆度的增加,折弯程度越来越小。而当桥丝的初始角度为90º时,桥丝均被拉伸,随着椭圆度的增加,拉伸率不断增加,若拉伸率大于桥丝材料本身的拉伸率时,则桥丝断裂。当桥丝的初始角度靠近45º时,桥丝被拉伸或折弯的程度较小。从总体上来说,桥丝拉伸率的绝对值随椭圆度的增加而增加。
4.2 桥丝电阻的变化
根据式(8),在桥丝的初始角度分别为0、30°、45°、60°和90°时,计算桥丝的电阻变化率随电极塞椭圆度的变化,结果如图9所示。
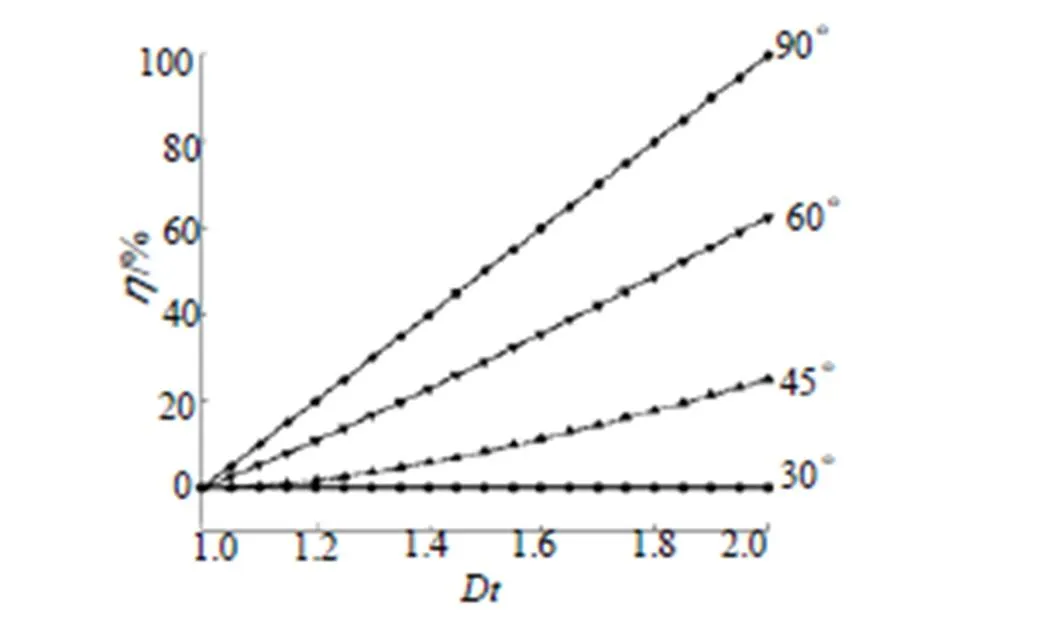
图9 桥丝电阻变化率与椭圆度之间的关系
从图9的结果可以发现,当桥丝的初始角度小于30°时,桥丝的电阻变化率为0,即桥丝未被拉伸。而当初始角度大于30°时,随着电极塞椭圆度的增加,桥丝的电阻变化率也随之增加,且初始角度越大,电阻变化率也越大。
4.3 桥丝受拉的临界初始角度
临界初始角度被定义为:当桥丝的初始角度为某一角度时,过载之后,桥丝既不会被拉伸,也不会被折弯,则称该角度值为临界初始角度。在式(3)中,若令桥丝的拉伸率为0,并结合式(5),即可得到桥丝不被拉伸时的临界初始角度α。若桥丝的初始角度大于α时,桥丝被拉伸,易发生断裂。计算得到了临界初始角度随椭圆度的变化规律,如图10所示。
从图10的结果可以看出,桥丝的临界初始角度随电极塞横截面椭圆度的增加而增加。另一方面,若要使桥丝不被拉伸,桥丝的初始放置角度必须小于45°。
综上所述,横向过载时,电极塞的放置方向或角度对电雷管的受载损伤影响较大。若要避免桥丝的受载损伤,桥丝初始角度越小越好,电雷管的最佳放置方式是使桥丝平行于电雷管的运动方向。

图10 临界初始角度与椭圆度之间的关系
5 结论
根据解析几何学的基本原理,建立双脚线电雷管的桥丝在横向过载时受拉损伤的计算模型。利用该模型计算桥丝的初始角度、桥丝拉伸率以及电阻变化率随电极塞椭圆度的变化规律。
(1) 计算模型具有较好的可靠性。电雷管的桥丝拉伸率、临界初始角度均随电极塞横截面椭圆度的增加而增加;
(2) 若要避免桥丝的受载损伤,电雷管的最佳放置方式是使桥丝平行于电雷管的运动方向。
(3) 通过模型计算,为火工品的抗横向过载加固和结构设计提供理论支撑。
[1] Liu Y, Ma A, Huang F. Numerical simulations of oblique -angle penetration by deformable projectiles into concrete targets[J]. International Journal of Impact Engineering, 2009, 36(3): 438-446.
[2] Roisman I V, Weber K, Yarin A L, et al. Oblique penetration of a rigid projectile into a thick elastic plastic target: theory and experiment[J]. International Journal of Impact Engineering, 1999, 22(7): 707-726.
[3] 李媛媛,贾宪振,高立龙. 弹体斜侵彻混凝土过程中炸药的动态响应[J]. 四川兵工学报, 2013, 34(9): 36-38.
[4] 徐文旭,张靖,齐占元,等. 子母弹抛撒内弹道建模及仿真[J]. 兵工学报, 2006, 27(5): 797-801.
[5] 王帅,陶如意,王浩,等.子母弹内燃式气囊抛撒内弹道建模及数值仿真[J].弹道学报, 2009, 21(3): 57-60.
[6] 李创新,沈瑞琪,刘卫.高加速度冲击过载下桥丝式电雷管的损伤特性研究[J].火工品, 2012(3): 1-4.
[7] 李创新. 高过载条件下桥丝式电雷管损伤特征和规律研究[D]. 南京:南京理工大学, 2013.
Damage Model for Bridge Wire of Electric Detonator Under High-g Loading
LIU Wei, SUN Xiao-xia, SHEN Rui-qi,WU Li-zhi
(School of Chemical Engineering, Nanjing University of Science and Technology, Nanjing,210094)
Based on the basic principle of analytic geometry, a model was built to describe the tensile damage process of bridge wire of double-wires electric detonator under lateral high-g loading. The tensile ratio, critical initial angle and resistance value of the bridge wire were obtained. Results show that the tensile ratio, critical initial angle and resistance value increase gradually with the ovality of the electrode plug increasing. The bridge wire is not stretched when the initial angle is less than 45º, and the best way to put the detonator is to keep the bridge wires parallel with the impacting orientation. The model results agree well with the ANSYS/LS-DYNA simulation results, and the model can accurately describe the damage characteristic of the bridge wire under lateral high-g loading.
Electric detonator;Bridge wire;High-g loading;Air gun;Lateral damage
1003-1480(2014)05-0001-05
TJ450.1
A
2014-05-25
刘卫(1986-),男,博士研究生,主要从事冲击动力学及火工品抗过载性能测试与评估。
江苏省普通高校研究生科研创新计划资助(CXZZ11_0271)。
