CFD方法在刺激剂扩散模拟中的有效性验证
2014-07-12徐路程肖凯涛宋伟伟
徐路程,肖凯涛,宋伟伟
CFD方法在刺激剂扩散模拟中的有效性验证
徐路程,肖凯涛,宋伟伟
(防化研究院,北京,102205)
基于计算流体力学(CFD)方法,对某型刺激剂在平坦开阔地区的扩散进行模拟,并与实验结果进行对比,从而验证了CFD方法对于模拟刺激剂在各种风速条件下扩散的有效性,为其在复杂地形环境中的模拟奠定理论基础。
刺激剂;扩散模拟;计算流体力学;验证
刺激剂可以通过燃烧、爆炸、机械喷洒等方式施放到大气中,在大气中扩散形成气溶胶,由于在复杂环境中难以对刺激剂进行测试试验,因此很难了解不同的气象条件下、复杂环境中刺激剂能够达到的效能。而数值模拟方法能够模拟出刺激剂在不同地形、不同气象条件下的扩散,进而为其在复杂环境中的使用提供技术支持。
目前,国内外已有多项研究使用计算流体力学方法对气溶胶污染物的扩散进行模拟[1-4],这些模拟都是在稳态条件(即假定各物理量随时间基本保持稳定)下进行的,显然不适合模拟刺激剂的施放过程的瞬态性。因此,本文以某型刺激剂为例,使用计算流体力学方法对平坦开阔地条件下的刺激剂的施放进行模拟,与实验结果进行对比,以验证计算流体力学方法对于刺激剂扩散模拟的适用性,并为这种方法运用于复杂地形环境下刺激剂扩散模拟奠定理论基础。
1 计算流体力学方法
1.1 几何模型
用于数值模拟的几何模型如图1所示,计算域为140m×140m的正方形区域,在图中释放点处建立直角坐标系,距离计算区域的右边界和下边界分别为10m,模拟的风向为东偏南25°。由于气溶胶扩散在空间中是一个三维的过程,并且扩散过程一般都发生在大气边界层以内。因此,本模型中考虑垂直方向的计算高度为40m,于是,三维的计算区域为140m×140m×40m。
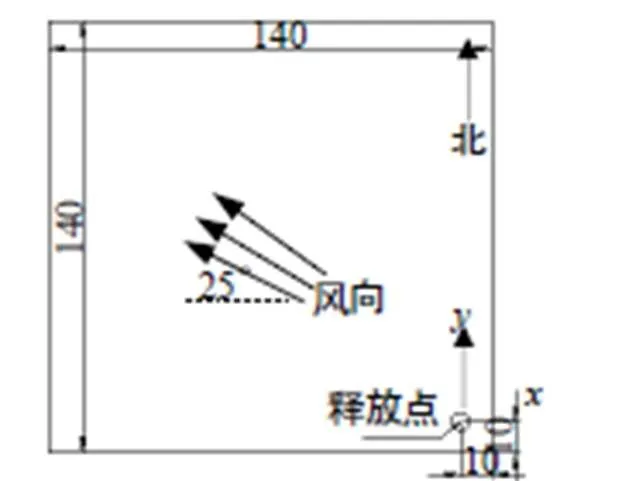
图1 计算区域示意图
1.2 数学模型
数学模型基于以下假定:(1)流动为不可压缩流动。由于大气边界层中的流速远小于声速,因此可以假定流动为不可压缩流动;(2)流动为稳态流动。文献[5]中采用了这种假定,这种稳态实际上是一种“伪稳态”(pseudo- steady-state),能够代表边界层中一段时间内相对稳定的一种流动状态,这种状态也是适合于刺激剂扩散的一种风场条件。
湍流是大气边界层中的主要运动形态,对动量输运、热量输送以及物质输送起着主要作用[6]。而计算流体力学方法中目前有3类方法模拟湍流[7]:直接数值模拟(DNS,Direct Numerical Simulation)方法,大涡模拟(LES,Large Eddy Simulation)方法,雷诺时均方程模拟(RANS,Reynolds Average Numerical Simulation)方法。这3种方法的区别在于模拟湍涡尺度范围的不同。RANS方法从实际工程应用的角度出发,将物理量都分解为平均项和脉动项,但由于引入了脉动项,就需要引入相应的方程来描述脉动项,也就是要考虑加入所谓的湍流模型来使方程组封闭。由于较高的稳定性和效率,-模型及其变种是最为常用的湍流模型[8]。本研究中将采用RANS方法中的-模型对湍流进行模拟。
基于以上假定和湍流模型的选取,流体的控制方程组(张量形式)如下:

(2)
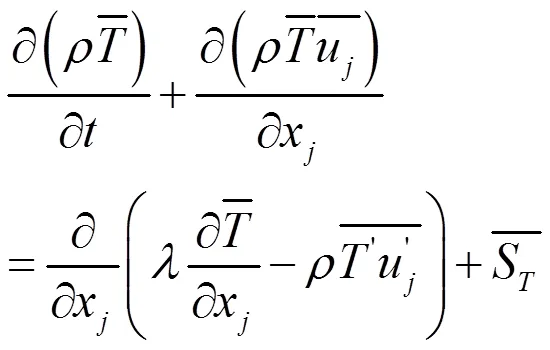
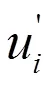
1.3 边界条件
边界条件的设定如图2所示。
(1)东侧、南侧边界设定为速度边界条件,并且采用《环境影响评价技术导则大气环境部分》所建议的幂指数风廓线,在计算中通过使用Fluent软件的UDF(User Defined Function,用户自定义函数)实现:
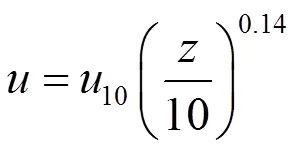
实验中风速一般是由距地2m高的风速仪得到的,而上述公式中需要的是10m高度的风速。因此,需要首先推导2m风速和10m风速的关系:
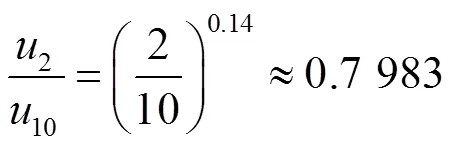
10≈1.252 72(6)
模拟中2m高度的风速的取值以及对应的10m高处的风速大小如表1所示。
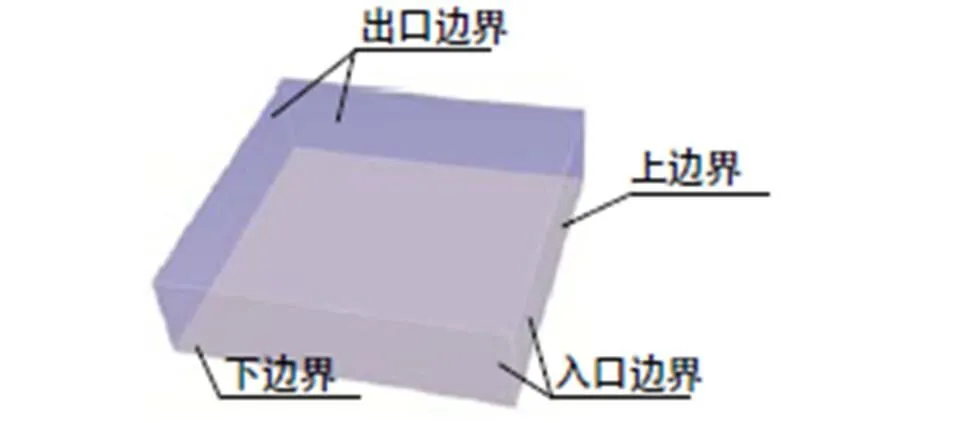
图2 三维几何模型及边界条件
表1 2m高度风速和10m高度风速的对应关系 (m·s-1)
Tab.1 Correspondence table between2and10

模拟的风向取为实验时较为稳定的风向:东偏南25°,即与轴负向成25°,如图1所示。温度梯度取为-0.3K/m,2m高度处测得的温度为8℃,因此垂直方向的温度分布为:
()=281.15+0.3(-2) (7)
温度廓线在Fluent中同样使用UDF实现。
(2)西侧、北侧边界设定为外流边界,即所有的物理量在此边界条件处都满足梯度为零的条件。
(3)上边界设定为对称边界,即此处物理量的法向速度为零,法向梯度也为零。
(4)下边界设定为壁面边界,即无滑移边界,这种边界代表了在边界上的法向和切向的速度均为零。而根据温度分布的要求,此处的温度应设置为:280.55K。
1.4 网格划分
本研究使用Gambit软件对几何模型进行网格划分,Gambit提供了多种网格划分的方式,而由于要在释放点附近进行局部的加密,因此选择能够灵活划分的非结构网格。本研究中采用如下网格划分形式:水平方向上,靠近释放点处的网格大小设置为0.5m,远离释放点处的网格大小设置为2m,这是因为释放点周围的物理量变化会较快,较密的网格能够较为准确地表现出这种变化;垂直方向上由于在靠近壁面处的物理量变化较快,因此要布置稍密的网格,而在远离下边界的上层,可以布置较为稀疏的网格。于是,在靠近地面处布置初始网格的尺寸为0.5m,垂直方向上共布置40个网格,沿着垂直向上的方向均匀增长;整个三维空间区域使用非规则的三棱柱网格进行划分,整个计算区域共108×104个网格。
1.5 流场求解方法
本研究使用Ansys Fluent 12.0对控制方程进行求解。(1)控制方程离散:动量方程、能量方程、湍动能方程和湍流耗散率方程使用二阶迎风格式进行离散,具有较好的精确度;压力使用body-force - weighted方法,这种离散方法适用于存在自然对流的情况。(2)压力速度耦合方式:选择SIMPLEC算法对压力速度进行耦合[7]。(3)残差设定:为了保证计算结果的收敛性,将能量方程的收敛准则设定为10-6(标准化残差),其他方程的收敛准则设定为10-3(标准化残差),同时,在计算过程中还对空间中一点进行监测,2m高度风速大小为1m/s时的监测结果如图3所示,其他风速条件下的风场收敛监测结果是类似的。从标准化残差图中可以看到各个指标基本收敛,但收敛到什么程度并不是很直观。收敛的最终目的是使计算域中的物理量无限地逼近真解,因此,采用对一点监测物理量的办法能够更加清楚的说明这一点,如图4所示,计算域中空间坐标为(0,0,2)的点的速度大小已经在迭代的过程中逐渐收敛。

图3 标准化残差收敛图(u2=1m/s)

图4 流场中一点速度大小监测图(u2=1m/s)
图5 跨风截面位置示意图
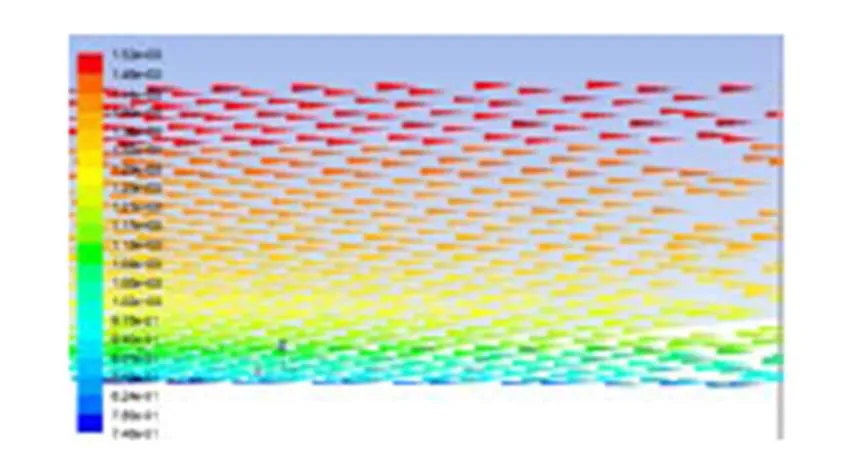
图6 跨风截面风速矢量图(u2=1m/s)
图5为跨风截面位置示意图,从跨风截面风速矢量图6可以看到,在整个跨风截面上,风速分布基本能够保持与入口相同的稳定状态,即整个计算区域的风廓线基本上保持与入口相同。这里与上相同,只使用2=1m/s的情况为例进行说明。
1.6 气溶胶扩散模拟
拉格朗日方法相对精度较高,求解复杂程度较低,而且能够适用于复杂地形的情况。因此,本研究中选用这种方法来模拟刺激剂的扩散。刺激剂的施放源的尺寸相比整个计算域的尺寸可以忽略不计,因此研究中考虑使用点源来模拟释放源,点源的属性如下:施放位置位于空间原点上方0.1m高度位置,空间坐标为(0,0,0.1);施放方向为沿着风速方向,空间向量为(-0.906,0.423,0);施放时间为0~30s;粒子粒径为10μm;燃烧粒子的温度假定为100℃(373.15K);初始速度相比风速较小,假定为0.1m/s;锥形点源的半角为15°,出口半径为0.01m;防暴弹总药量为50g,燃烧后有效作用率为21%,即有效药量为13.5g,由此可以估算得到:弹药的平均质量流率为0.000 45kg/s;弹药的材料密度为1 296kg/m3。模拟扩散的总时间为60s,时间步长取为0.1s,共600个时间步。可以使用空间中一点的1min剂量(mg·min/m3)[10]来衡量刺激剂在1min内的累计作用效果:
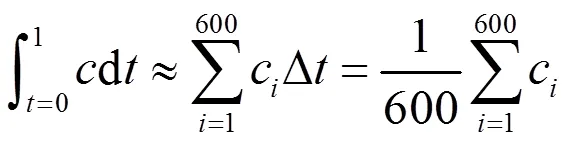
式(8)中的约等号是表示用数值积分来近似表示解析积分,具体的数学含义是:通过计算可以得到0.1s到60s,600个时刻的浓度计算结果,可以记为c(=1,…,600),可以假定用第个时刻的瞬时浓度代表从-1时刻到时刻之间的平均浓度,于是1min内的平均浓度可以表示为(8)最右端所示。
而对于关注的=1.5m高的平面上的每个结点都可以通过式(8)求出1min剂量,但Fluent软件没有提供这一功能。因此,本研究中使用C#语言编写程序,分别读取各个时刻的计算结果文件,将平面上每个点的浓度数据累加,最后得到1min剂量。
2 实验验证
2.1 实验材料
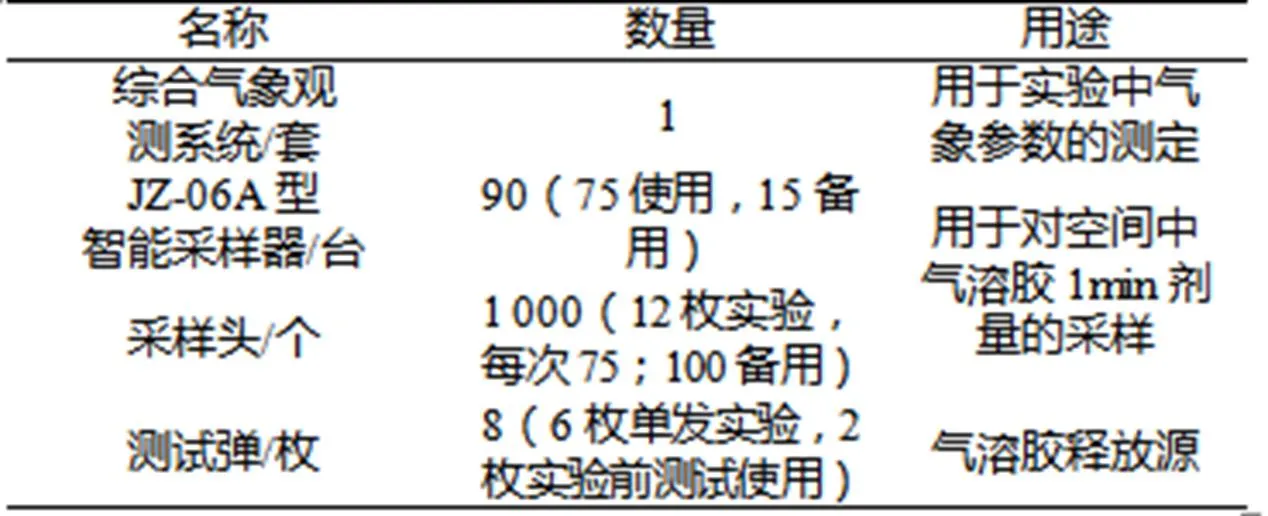
验证实验中所需要的测量仪器及测试弹药的数量及用途如表2所示。
表2 实验仪器及弹药
Tab.2 Experimental apparatus and ammunition
2.2 实验方法
实验中,采样器布设方案如图7所示。实验时,当地气象条件为:风向东偏南25°,温度8℃,温度梯度约为0.3K/m。风速与模拟中的2m高度的风速一致。当通过综合气象观测系统测量到的风速基本稳定于期望风速时,引爆测试弹,同时采样器开始同步采样。弹爆1min后,采样器停止采样。

图7 标场及采样点布置方案示意图
2.3 结果分析
本研究中涉及的刺激剂的有效1min剂量为0.86mg·min/m3。在实际使用中,决策者更为关注的是有效浓度能够达到的空间范围。因此,对1.5m高度平面(人体站立呼吸平面)上有效浓度以上的区域的长、宽、面积及最大剂量值进行统计。
首先绘制阈值剂量的等值线以确定有效区域,阈值等值线的绘制由软件Surfer 8.0实现。由于Fluent计算得到的结果不是规则的网格分布,而Surfer中使用的等值线生成算法是基于结构化网格的。因此,在Surfer软件中首先要将非结构化的数据插值到结构网格上,将非结构数据格式转换为结构化的网格文件形式(.grd)。克里金法是对空间数据求最优、线性、无偏内插估计量的方法,所绘制的浓度等值线既能保持数据的细节又可尽力地表现数据的变化趋势,能够最大程度地利用所给的信息分析数据空间的边界,具有很高的空间外推精度。因此,本研究中选择克里金法对Fluent计算的数据进行网格化处理。实验数据的处理方法是类似的,不过,在网格化数据之前,要首先把极坐标系表示的采样点坐标转化为直角坐标系表示的坐标。Surfer对Fluent模拟结果和实验数据的统计结果的对比曲线如图8所示。
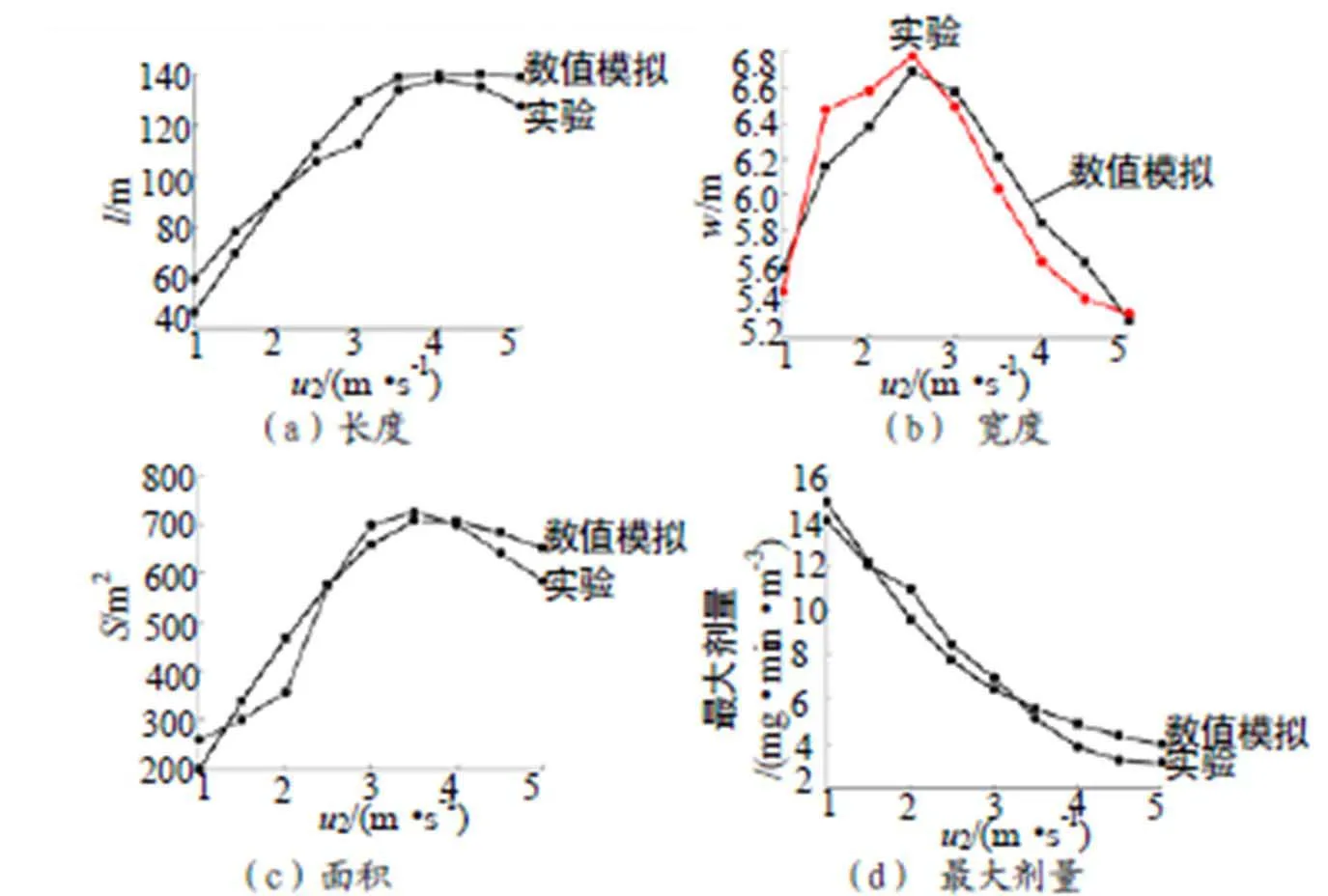
图8 有效区域面积与风速关系图
对比图8几条曲线可以看到,各种指标在各种风速条件下都比较接近:有效区域长度的最大相对误差为21.850%;有效区域宽度的最大相对误差为5.85%;有效区域面积的最大相对误差为30.398%;有效区域的最大剂量的最大相对误差为12.413%。
另外,数值模拟结果和实验结果在随风速变化的规律上都体现出相同的趋势。由图8(a)可见:当风速小于4m/s时,随风速增加有效区域长度增加;风速超过4m/s时,有效区域长度随风速增加减小。由图8(b)可见:当风速小于2.5m/s时,随风速增加,有效区域宽度增加;风速超过2.5m/s时,有效区域宽度随风速增加减小。由图8(c)可见:当风速小于3.5m/s时,随风速增高,有效区域面积变大;风速超过3.5m/s时,有效区域面积随风速增高而变小。由图8(d)可见:对于所有风速,随着风速增加,最大剂量值会一致性地下降。
3 结语
本文首次将计算流体力学方法应用于刺激剂的扩散模拟,并将模拟结果与实验结果进行了对比。对比显示在各个风速条件下,模拟结果与实验结果的各指标的误差都不超过40%,这证明了计算流体力学方法用于刺激剂扩散模拟的可行性和有效性,从而表明计算流体力学方法可以作为复杂地形条件下刺激剂作用效能评估研究的理论基础。
[1] Riddle A, Carruthers D, Sharpe A, et al. Comparisons between FLUENT and ADMS for atmospheric dispersion modelling[J]. Atmospheric Environment, 2004, 38(7): 1 029-1 038.
[2] Di Sabatino S, Buccolieri R, Pulvirenti B, et al. Flow and pollutant dispersion in street canyons using FLUENT and ADMS-Urban[J]. Environmental Modeling & Assessment, 2008, 13(3): 369-381.
[3] Pullen J, Boris J P, Young T, et al. A comparison of contaminant plume statistics from a Gaussian puff and urban CFD model for two large cities[J]. Atmospheric Environment, 2005, 39(6): 1 049-1 068.
[4] 金颖, 周伟国. 烟气扩散的 CFD 数值模拟[J]. 安全与环境学报, 2002, 2(1): 21-23.
[5] Cheng W C, Liu C H, Leung D Y C. On the correlation of air and pollutant exchange for street canyons in combined wind-buoyancy-driven flow[J]. Atmospheric Environment, 2009, 43(24):3 682-3 690.
[6] 盛裴轩,毛节泰,李建国,等.大气物理学[M].北京:北京大学出版社,2003.
[7] 吴清松.计算热物理引论[M].合肥:中国科学技术大学出版社,2009.
[8] Li X X, Liu C H, Leung D Y C, et al. Recent progress in CFD modelling of wind field and pollutant transport in street canyons[J]. Atmospheric Environment, 2006, 40(29): 5 640- 5 658.
[9] 蒋维楣,孙鉴宁,曹文俊.空气污染气象学教程(第二版)[M].北京:气象出版社,2004.
[10] 《核生化防护大辞典》编辑部.核化生防护大辞典[M].上海:上海辞书出版社,2000.
The Validation of CFD Method in Simulation of Irritant Dispersion
XU Lu-cheng, XIAO Kai-tao, SONG Wei-wei
(Research Institution of Chemical Defense, Beijing,102205)
Based on the principle of computational fluid dynamics (CFD) method, the dispersion of some kind of irritant in flat, open terrain was simulated. By comparing with experimental result, the effectiveness of CFD method in modeling irritant dispersion under the condition of different wind velocities is verified, which establishes the theoretical foundation for its simulation in complex terrain.
Irritant;Dispersion simulation;Computational fluid dynamics;Validation
1003-1480(2014)05-0042-05
TQ567.5
A
2014-05-13
徐路程(1990-),男,在读硕士研究生,主要从事防暴弹药性能评价及使用技术研究。
总装备“十二五”部预先研究课题。
