Maple在微分几何实践教学中的应用

周俊东

（阜阳师范学院 数学与计算科学学院，安徽 阜阳 236037）

Maple在微分几何实践教学中的应用

周俊东

（阜阳师范学院 数学与计算科学学院，安徽 阜阳 236037）

利用Maple的符号计算和图形绘制功能，以典型实例介绍了Maple在微分几何实践教学中应用，改进了微分几何的教学方法，有利于提高学生的学习兴趣和运用软件解决实际问题的能力。

微分几何；Maple；曲率；基本形式

微分几何主要以数学分析为工具，研究空间形式，并适当采用张量分析的方法讨论曲线和曲面的分析性质。开设这门课程旨在使学生掌握三维欧氏空间中曲线和曲面的基本理论，进一步提高分析运算能力和空间想象能力，并为学习黎曼几何、微分流形等后继课程打下基础。在教学中，如何激发学生对微分几何的兴趣，增强学生解决几何问题的能力，以提高教学质量，已成为数学教学改革的重要课题。Maple是一种具有强大符号计算和数学分析能力的软件，具有很强的数据可视化能力，另外Maple提供了一种结构化的内部编程语言，类似于C、BASIC等第四代高级语言，使用户可以快速地设计编写自己的程序。Maple在教学中有着广泛的应用[1-8]。

本文讨论了Maple在微分几何教学中的应用，它不仅可以简化计算，而且还可以绘制曲线和曲面的图形，从而可以更加直观地帮助学生理解微分几何的理论。

1 Maple计算功能在微分几何实践教学中的应用

微分几何课程中有一些公式计算比较复杂，例如曲线的曲率和挠率以及曲面的高斯曲率和平均曲率计算。我们可以利用Maple的计算功能辅助计算，提高学生的计算能力。

1.1 空间曲线上任意一点的曲率和挠率计算

曲率和挠率刻画了空间曲线在一点邻近的弯曲程度和扭曲情况，曲线论的基本定理证明了除空间位置差别之外，空间曲线形状可以由曲率和挠率唯一确定。设C3类曲线参数方程为，则曲率。曲率和挠率是曲线论中的核心概念，根据公式计算曲率和挠率，比较复杂，我们可以利用Maple来简化计算。下面以曲线论中的经典曲线——圆柱螺线为例，求圆柱螺线={a cost,a sin t,b t}(-＜t＜)的曲率与挠率。

打开Maple软件，在主界面输入程序语句计算曲率和挠率：

1.2 关于曲面第一基本形式和第二基本形式的计算

在Maple命令窗口输入以下程序语句：

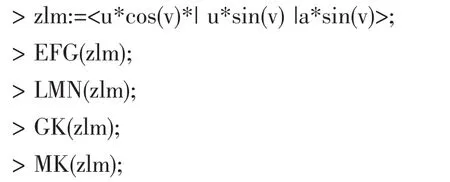
2 Maple的图形绘制功能在微分几何实践教学中的应用

为了加强学生对几何中一些原理的理解，我们在教学中经常要作图。手工绘制三维图形不仅浪费时间，而且制作的图形也不够准确；另一方面微分几何中的原理常常表现为变换中存在不变，为了描述这种现象，就需要作动态图。以上问题我们可以采用Maple作图，根据所学的几何原理画出动态的几何图形。

圆柱螺线和圆锥螺线在曲线论中是两个经典的例子。圆柱螺线可以看成一个质点围绕圆柱面的运动轨迹，这个运动可以分解成绕圆柱面匀速转动和向上匀速直线运动，圆柱螺线具有常的曲率和常的挠率。圆锥螺线稍稍复杂一些，它的曲率和挠率都是变化的。下面我们用Maple软件绘制圆柱螺线和圆锥螺线的图形。在Maple中输入以下程序语句：

绘制出的图形如下图1和图2。

正螺面和悬链面是曲面论中典型的例子。正螺面的坐标网是正交的渐进网，是非可展的直纹面，同时又是极小曲面。微分几何中证明了极小的旋转曲面一定是悬链面，而悬链面和正螺面又是等距的。下面我们绘制出正螺面和悬链面的图形，输入以下程序语句：

绘制出的正螺面如图3，悬链面如图4。

图1 圆柱螺线

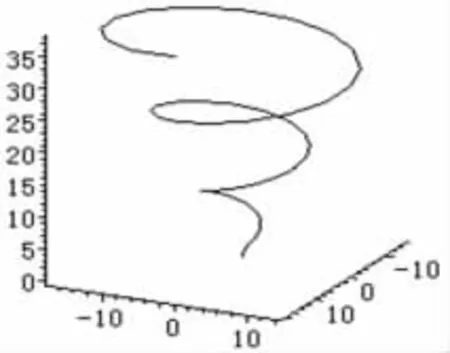
图2 圆锥螺线

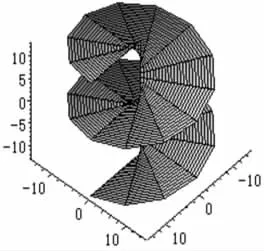
图3 正螺面

图4 悬链面

以上利用Maple作出的图形可以转换不同的视角给学生观看，也可以作出动态的图形，很好地体现了Maple的绘图功能在微分几何教学中的实践应用性。

3 结束语

Maple为微分几何实践教学提供了一个非常好的平台，它具有超强的符号计算功能和3D绘图功能。教师运用软件辅助教学，能够把抽象的几何理论形象地展示出来。学生在学习中使用软件，可以省去大量复杂的手工计算，更加容易接受所学的理论。Maple应用于微分几何实践教学可以调动学生的学习兴趣，提升学生的计算能力和创新能力，从而获得更好的教学效果。

[1]阿荣．Maple在线性代数教学中的应用[J]．高等数学研究，2013，16(4)：97-99．

[2]周甄川，吕同斌．Maple的图形绘制功能在高等数学教学中的应用[J]．黄山学院学报，2010，12(3)：117-119．

[3]胡源艳．Maple在高等代数与解析几何教学中的应用[J]．高等函授学报：自然科学版，2012，25(6)：36-39．

[4]朱春蓉，郑群珍．Maple在常微分方程教学中的应用[J]．河南教育学院学报：自然科学版，2009,18(3)：63-64

[5]额尔敦布和，白秀，王海清．Maple软件在数学分析中的应用研究[J]．内蒙古民族大学学报：自然科学版，2013，28(2)：146-149．

[6]余柏林，程虹，严文利．基于Maple的高等代数与解析几何可视化教学探究[J]．教育与教学研究，2013，27(1)：72-75.

[7]刘琼．Maple软件在复变函数中的应用[J]．邵阳学院学报：自然科学版，2013,10(1)：21-25．

[8]罗日才．基于Maple的曲面在一点临近结构的三维可视化教学[J]．高师理科学刊，2010，30(1)：:85-87．

[9]梅向明，黄敬之．微分几何[M]．北京：高等教育出版社，2008．

[责任编辑：桂传友]

O186

A

1674-1104(2014)03-0126-03

10.13420/j.cnki.jczu.2014.03.037

2013-12-13

国家特色专业教研项目（TS11496）；安徽省教学研究项目（2012jyxm344）；安徽省教育厅科研项目（KJ2013Z263）。

周俊东（1983-），男，安徽肥东人，阜阳师范学院数学与计算科学学院讲师，硕士，主要研究方向为微分几何。