三维Minkowski空间中的k-型伪零螺线

钱金花， 刘 杰

(东北大学 理学院， 辽宁 沈阳 110819)

在三维欧氏空间中，若一条曲线的切线和固定方向成固定角，则称其为一般螺线[1].近年来，欧氏空间中一般螺线的定义已经被推广到Lorentz-Minkowski空间中[2-4]. 本文给出k-型(k=1，2，3)伪零螺线及其轴的定义，并根据定义的伪零曲线的结构函数，讨论各种伪零螺线的几何性质.

1 预备知识

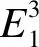
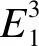
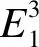
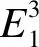
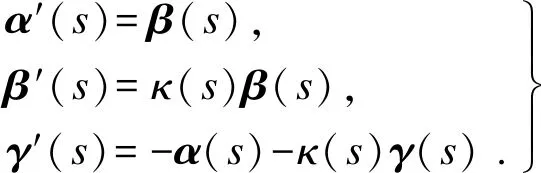
(1)

其中：

〈α，α〉=〈β，γ〉=1，〈β，β〉=〈γ，γ〉=0，

〈α，β〉=〈α，γ〉=0.α(s)，β(s)，γ(s)分别称为曲线r(s)的切向量、主法向量和副法向量；κ(s)称为曲线r(s)的曲率函数.

标注1 本文所讨论的伪零曲线均以弧长s为参数.

首先，设伪零曲线r(s)的单位切向量为

r′(s)=[ξ1(s)，ξ2(s)，ξ3(s)].

显然-ξ12+ξ22+ξ32=1.不失一般性，设

这里f，g是s的光滑函数.于是

另外，由〈r″(s)，r″(s)〉=0，经过计算，有

(g2-1)f′=2fg′.

解上面的微分方程，可得

总结上面的推导过程，有如下结论.

其中：f，g是s的光滑函数，称其为结构函数，且它们满足

由引理2与引理1，容易得到如下结论.

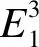
标注2 定义2中曲线r(s)的切向量α，主法向量β，副法向量γ都不是常向量.

2 主要结论

设非零常向量V是k-型伪零螺线r(s)的轴.那么V可以表示为[10]

V=v1α(s)+v2β(s)+v3γ(s) .

(2)

这里vi=vi(s)(i=1，2，3)是弧长参数s的光滑函数.显然

v1=〈α，V〉，v2=〈γ，V〉，v3=〈β，V〉.

在式(2)两端关于参数s求导，整理可得

(3)

2.1 1-型伪零螺线

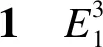
证明 根据1-型伪零螺线的定义，有

〈α，V〉=v1=C0(C0≠0).

(4)

在式(4)两端关于参数s求两次导，可知r(s)的曲率函数κ(s)是任意函数.

反之，对于任意伪零曲线r(s)，由式(3)和式(4)，总可以找到常向量

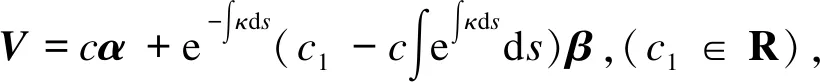
由定理1及引理3，不难得到下面的推论，具体证明略.

推论1 设r(s)是1-型伪零螺线，那么r(s)的轴V是类空轴，且V可以由r(s)的结构函数表示为

V=cα+(g′)-1(c1-cg)β.

这里c1，c∈R且c≠0.

2.2 2-型伪零螺线

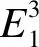
证明 根据2-型伪零螺线的定义，有

〈β，V〉=v3=C0(C0≠0).

将v3=C0代入式(3)中，可得曲率函数κ(s)≡0.此时由式(1)可知主法向量β为常向量，显然矛盾.证毕.

2.3 3-型伪零螺线

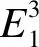
κ″(s)=κ′(s)κ(s).

进一步，曲率函数κ(s)有以下三种形式：

①κ(s)=-2(s+c1)-1；

②κ(s)=2atana(s+c2)；

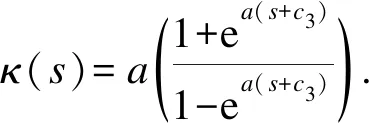
这里a>0且ci(i=1，2，3)∈R.

证明 根据3-型伪零螺线的定义，有

〈γ，V〉=v2=C0(C0≠0).

(5)

在式(5)两端关于参数s求导，可得

〈α，V〉+κ〈γ，V〉=0.

(6)

将v2=C0及式(6)代入式(3)中，可得

κ″(s)=κ′(s)κ(s).

(7)

通过降阶法解方程(7)，得到曲率κ(s)的具体表达式，如定理3中的①，②，③.

反之，当曲率κ(s)满足定理3中的①，②，③时，可以找到相应的常向量V如下：

①当κ(s)=-2(s+c1)-1时，有

②当κ(s)=2atana(s+c2)时，有

V=-2catana(s+c2)α+cβ-

2ca2sec2a(s+c2)γ;

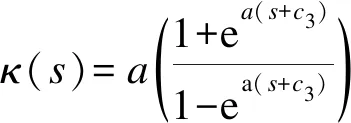
显然三种情形均满足〈γ,V〉=c≠0.证毕.

由定理3中的三种情形，有下面的推论.

推论2 设r(s)是3-型伪零螺线，那么

①当κ(s)=-2(s+c1)-1时，轴V为类光轴；

②当κ(s)=2atana(s+c2)时，轴V为类时轴；

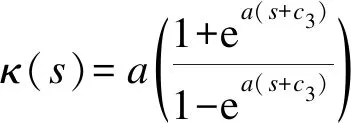
这里a>0且ci(i=1，2，3)∈R.

由定理3、引理2、引理3，通过适当的参数变换，可以得到如下结论，具体证明略.

定理4设r(s)是3-型伪零螺线，那么r(s)的结构函数为

①当κ(s)=-2(s+c1)-1时，有

②当κ(s)=2atana(s+c2)时，有

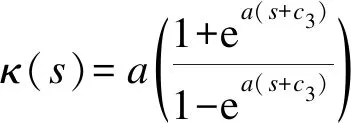
这里a>0且ci(i=1，2，3)∈R.

由定理4，引理2，有下面的推论.

推论3 设r(s)是3-型伪零螺线，那么

①当κ(s)=-2(s+c1)-1时，

r(s)=(ln|s|，-ln|s|，s)；

②当κ(s)=2atana(s+c2)时，

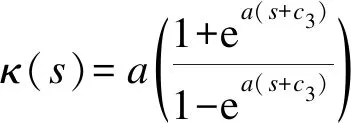
这里a>0且ci(i=1，2，3)∈R.

3 结 语

本文在三维Minkowski空间中定义了k-型伪零螺线，并找到了各类伪零螺线的轴.通过定义的结构函数给出了各种螺线的具体表达式.这为今后在不定度量空间中开展相关曲线的研究提供了一种新的思路.