基于双站红外跟踪临近空间目标研究*
2014-07-10秦雷李君龙周荻
秦雷,李君龙,周荻
(1.北京电子工程总体研究所,北京 100854; 2.哈尔滨工业大学,黑龙江 哈尔滨 150001)
0 引言
由于临近空间目标飞行速度快,具有较高的升阻比,且在大气层内长时间飞行,其运动轨迹往往呈现出“跳跃”特征,使用传统滤波估计方法和跟踪方式难以对飞行器实现准确的跟踪和轨迹预报,给跟踪定位临近空间飞行器带来了很大的困难。因此需要使用其他的滤波方法对目标进行定位跟踪,使其能够达到较好的效果。
由于无源定位系统具有作用距离远、隐蔽性好的优点,对于提高系统在电子战环境下的生存能力具有重要作用。对此,国内外许多学者做了大量的研究工作[1-2]。
在无源定位系统中,红外无源跟踪方式是指不向空中辐射任何能量,通过接收目标辐射的热能进行探测和定位,环境适应性较强,适合探测的目标范围较大。由于临近空间目标速度快,红外辐射强度大,本身不向外辐射无线电信号,不宜采用被动雷达跟踪方式,所以采用红外无源跟踪方式是最佳跟踪方式,其精度比被动雷达跟踪的精度要高。
根据平台数量不同,无源定位系统又可以分为单站和多站无源定位系统[3-4]。但是由于单站定位时间较长,易受到敌方攻击,生存能力较弱。相比来说,多站无源定位由空间上分布配置的接收机同时对辐射源信号进行接收处理,确定多个定位曲面,多个曲面相交,得到目标的位置,主要利用不同平台定位曲面之间差异较大的特点来定位和提高定位精度。
近年来,基于无源跟踪算法受到各国学者广泛的关注[5-10],而研究关于临近空间红外双站无源跟踪的文献偏少。由于双站相比单站平台数量较多,生存能力、抗敌方打击能力相比更强,探测目标速度更快、精度更高、探测距离更远,在反导、反临近空间高超声速飞行器等武器系统方面应用更加广泛,能够很好解决临近空间目标远距离探测和跟踪问题,因此本文以双站测向交叉定位为例对临近空间目标飞行器无源定位进行研究,并使用卡尔曼滤波算法进行仿真分析。
1 双站红外三维测向交叉定位算法
1.1 双站红外定位跟踪原理
假设2个无源测向系统分别设置在已知站址(x1,y1,z1)和(x2,y2,z2)处,在三维无源定位中分别测量方位角和俯仰角,即βi,αi(i=1,2),目标方位角βi会受到量测噪声的影响,该噪声是均值为0的高斯白噪声,标准差为σβ1和σβ2,则由2站分别获得的目标方向射线相交,即可实现对目标辐射源S的测向交叉无源定位。
9个元素的状态向量x由观察站跟踪系统、目标的相对位置P,相对速度v,目标加速度at组成。连续动力学系统在笛卡尔坐标系下可以表示为[11]

(1)
式中:
(2)
角度量测量的几何关系如图1所示。

图1 三维双站测向交叉定位示意图Fig.1 Sketch map of 3D bi-station cross location
角度量测量由方位角βi(i=1,2)和俯仰角αi(i=1,2)组成,它们可以被当作相对位置矢量的非线性函数,表示为
(3)
(4)
设r为观察站到目标的距离,A(a,b,c)为观察站的坐标位置,S(x,y,z)为目标坐标位置,得到三维测向交叉定位距离公式为
(5)
目标位置为

(6)
三维观察站与目标相对位置如图2所示。
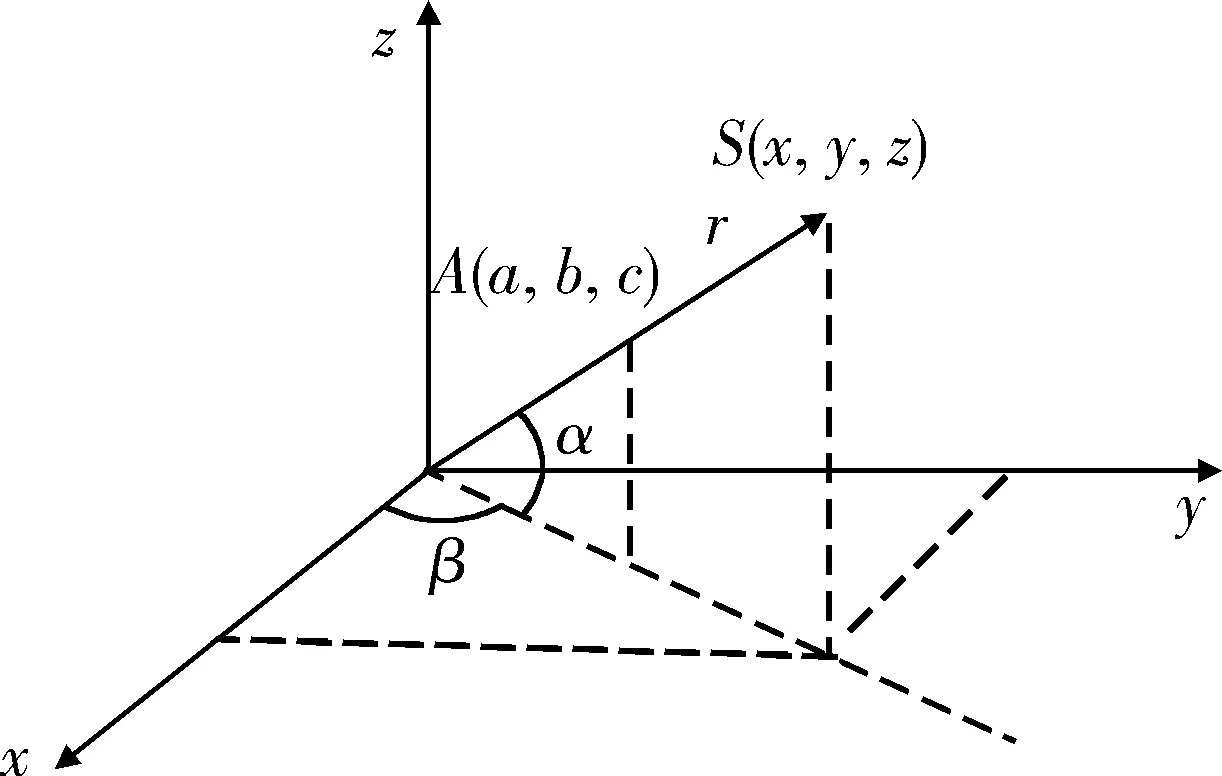
图2 三维观察站与目标相对位置示意图Fig.2 Sketch map of the relative position between 3D radar station and target
根据观察站A,B位置以及目标S位置,得出相对位置关系如图1所示。
从图2中可以得到:
(7)
联立求解式(7),可以得到图2中的目标位置坐标为
(8)
1.2 系统建模
考虑到临近空间目标飞行器大机动、大范围的特点,目标运动轨迹大致为正弦变化的跳跃弹道,类似于正弦机动模式。系统建模如下:
目标的机动性用过程噪声表示。系统状态方程可以表示为
X(n+1)=FX(n)+w(n).
(9)
状态转移矩阵F定义为
(10)
式中:Ts为采样间隔。
系统过程噪声向量为
w(n)中各个分量都服从零均值的过程高斯白噪声,其方差为
(11)

图2中,设第1个观察站A位置坐标为 (a,0,0),第2个观察站B位置坐标为(0,a,0),目标相对2个观察站以及原点的位置,速度,加速度的量测向量分别为
双站三维测向交叉定位系统模型确定了红外跟踪滤波的方式,这里具体体现在量测向量公式(12)中[12]。
量测向量设置为
Z(n)=(r1(n),r2(n),r3(n),vr1(n),vr2(n),vr3(n),ar1(n),ar2(n),ar3(n))T,
则量测方程可以设为
Z(n)=H(X(n)).
定义系统量测噪声向量为
V(n) = (vr1(n),vr2(n),vr3(n),vvr1(n),vvr2(n),vvr3(n),var1(n),var2(n),var3(n))T,
(13)
V(n)各个分量都服从零均值的量测高斯白噪声,其方差为
(14)
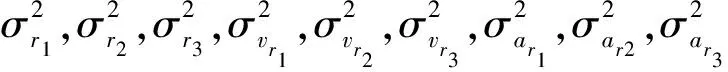
Z(n)=H(X(n))+V(n).
(15)
2 卡尔曼滤波算法
根据相应公式可以推导出离散卡尔曼滤波的递推公式如下:
(1) 动态方程
xk=Φk,k-1xk-1+Γk-1wk-1.
(16)
(2) 量测方程
zk=Hkxk+vk,k≥1.
(17)
(3) 验前统计量
Ewk=0,Cov(wk,wj)=Qkδkj,
(18)
Evk=0,Cov(vk,vj)=Rkδkj,
(19)
Cov(wk,vj)=0.
(20)
(4) 状态预测估计
(21)
(5) 方差预测
(22)
(6) 状态估计
(23)
(7) 方差迭代
[I-KkHk]Pkk-1.
(24)
(8) 滤波增益
(25)
(9) 初始条件
(26)
3 仿真分析

设定观察站量测位置误差为:均值为0,方差为0.5的3×2服从正态分布的矩阵。然后利用卡尔曼滤波算法对斜距估计误差、斜距估计相对误差进行了计算分析比较,总共进行了30次蒙特卡罗仿真试验。
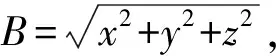
(27)
斜距估计误差为
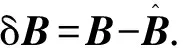
(28)
斜距估计相对误差为
(29)
利用卡尔曼滤波算法计算时,设置如下参数:
Hk=(1,0,0),过程噪声方差Qk-1=0。
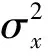
(30)
(31)
(32)
经过仿真计算,在假设的仿真条件下以及测向精度为0.1 rad时,相对斜距误差可以控制在0.035%以下。在其他条件不变的情况下,改变观察站的测向精度,得到相对斜距误差如表1所示。

表1 不同测向精度下的相对斜距误差 Table 1 Relative slant-range error under different DOA estimation accuracies
从表1中看出,改变测向精度对相对斜距误差存在一定的影响。
经过仿真得到三轴方向位置、速度、加速度误差如图3~5所示。

图3 三轴方向目标位置误差Fig.3 Three-axis target position error
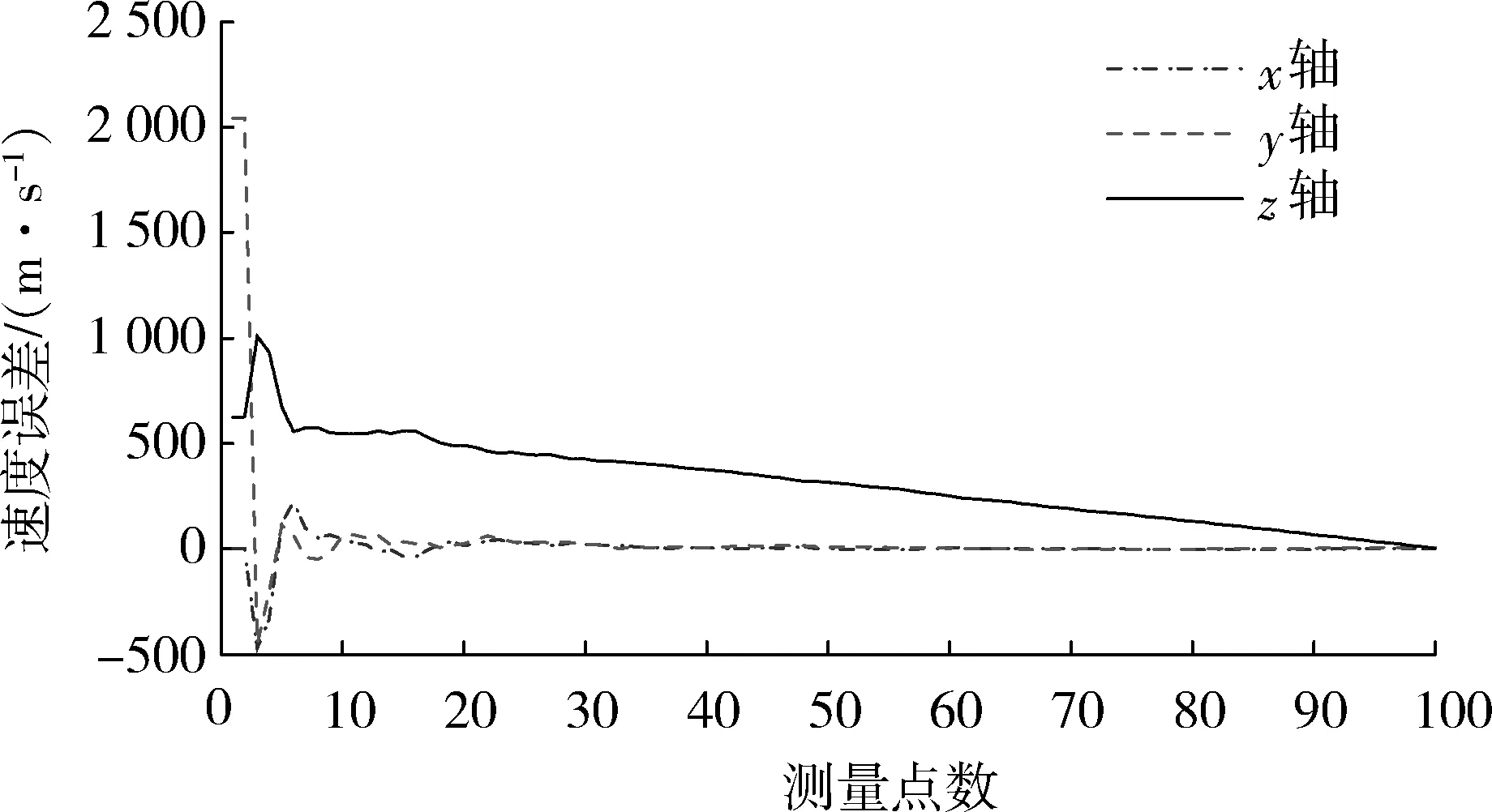
图4 三轴方向目标速度误差Fig.4 Three-axis target velocity error

图5 三轴方向目标加速度误差Fig.5 Three-axis target acceleration error
图3是仿真得到的目标位置在x,y,z三轴方向位置估计误差图,可以看出在x轴和z轴方向的位置误差可以保持在较小的范围内,趋于稳定。而y轴方向位置误差有发散的趋势。图4和图5分别是经过卡尔曼滤波后x,y,z三轴方向速度估计误差图和加速度估计误差图,可以看出图4中x轴和y轴速度误差基本保持稳定,z轴方向的速度误差逐渐减小。图5中在第10个测量点后三轴方向的加速度误差均趋于稳定,基本同时收敛到0附近。
在假设的仿真条件下以及测向精度为0.1 rad时,改变2个观察站之间距离,得到相对斜距误差如表2所示。

表2 不同站间距离时的相对斜距误差Table 2 Relative slant-range error under different distance between stations
从表2中看出,改变站间距离会对相对斜距误差产生影响。站间距离越大,则相对斜距误差越小。
4 结束语
机动目标跟踪问题近来年越来越受到国内外学者的关注,但是主要针对的是传统意义上的飞行器,对于临近空间飞行器的跟踪问题研究相对较少,并且多假设目标做匀速直线运动。针对这种情况,本文使用卡尔曼滤波算法,对临近空间飞行器双站红外定位跟踪问题进行了仿真分析,得到了斜距估计误差 、斜距估计相对误差。仿真结果表明卡尔曼滤波算法估计误差在规定的范围之内,跟踪滤波效果较好,对工程应用有一定的指导意义。
参考文献:
[1] 孙仲康,郭福成,冯道旺,等.单站无源定位跟踪技术[M].北京:国防工业出版社,2008:1-10.
SUN Zhong-kang, GUO Fu-cheng,FENG Dao-wang,et al. Passive Location and Tracking Technology by Single Observer[M].Beijing:National Defense Industry Press,2008:1-10.
[2] Branko Ristic,Sanjeev Arulampalam M. Tracking a Manoeuvring Target Using Angle-Only Measurements:Algorithms and Performance[J].Signal Processing,2003,83(3):1223-1238.
[3] 陈玲,陈德煌. 多站无源定位系统中的机动目标跟踪算法[J].电讯技术,2010,50(11):10-14.
CHEN Ling,CHEN De-huang. Tracking Algorithm for Maneuvering Target in Multiple Passive Sensor System[J].Telecommunication Engineering, 2010,50(11):10-14.
[4] 陈玲.无源定位与跟踪技术研究[D].北京:北京航空航天大学,2004.
CHEN Ling.Study of Passive Location and Tracking Technique[D].Beijing:Beijing University of Aeronautics and Astronautics,2004.
[5] NOROUZI Y,DERAKHSHANI M.Joint Time Difference of Arrival/Angle of Arrival Position Finding in Passive Radar[J].IET Proceedings on Radar,Sonar & Navigation,2009,3(2):167-176.
[6] BISHOP AN,BRIAN DO,FIDAN B,et al. Bearing-Only Localization Using Geometrically Constrained Optimization[J].IEEE Trans. on Aerospace and Electronic Systems,2009,45(1):308-320.
[7] BISHOP A N,PATHIRANA P N.Trajectory Characterizations for a Discrete-Time Bearing-Only Navigation Strategy[C]∥Proc.of the 16th Mediterranean Conference on Control and Automation Congress Centre,Ajaccio ,France,2008:1186-1191.
[8] KHALOOZADEH H,KARSAZ A.Modified Input Estimation Technique for Tracking Manoeuvring Targets[J].IET Proceedings on Radar,Sonar & Navigation,2009,3(1):30-41.
[9] CHEN H,LIU C R,LI C.Data Association Algorithm for Passive Sensor System[C]∥Proc.of the First International Workshop on Education Technology and Computer Science.Wuhan,2009:970-974.
[10] YAIRI T,KANAZAKI H.Bearing-Only Mapping by Sequential Triangulation and Multi-Dimensional Scaling[C]∥Proc.of the IEEE International Conference on Robotics and Automation,Pasadera,USA,2008:1449-1454.
[11] SONG T L.Observability of Target Tracking with Bearings-Only Measurements[J]. IEEE Transactions on Aerospace and Electronic Systems,1996,32(4):1468-1472.
[12] 付天骄,周共健,田文,等.无角度双站地波雷达组合定位跟踪和滤波算法[J].系统工程与电子技术,2011,33(3):552-556.
FU Tian-jiao,ZHOU Gong-jian,TIAN Wen,et al. HF Ground Wave Bi-Station Radar Tracking and Filtering without Azimuthal Measurements[J].Systems Engineering and Electronics, 2011,33(3):552-556.
