基于PSGA的岸基导弹火力分配研究*
2014-07-10汲万峰王光源章尧卿孙钧正
汲万峰,王光源,章尧卿,孙钧正
(海军航空工程学院,山东 烟台 264001)
0 引言
遗传算法(genetic algorithna,GA)作为一种基于生物自然选择与遗传机理的随机搜索算法,因其在优化求解方面具有较强的优越性[1],因而在航迹规划问题中得到了广泛的应用[2-4]。但GA存在2个不容忽视的缺陷,分别是未成熟收敛和遗传后期的收敛迟滞[5]。主要原因是:一方面,为了保证算法的全局收敛性,就要维持种群中个体的多样性和搜索的有效性,避免有效基因的丢失;另一方面,为了加快收敛速度,就要使种群较快地向最优状态转移,这又会降低群体的多样性,容易陷入局部最优。如何较快地找到最优解并防止早熟收敛问题是GA的一个较难权衡的问题。
许多学者对GA的改进方法进行了研究,主要集中在2个方面:①对于GA自身过程算子或控制参数的不断完善和改进。如:分层遗传、自适应遗传、小生境、并行遗传等[6]。②引入其他优化思想或智能技术,发挥互补优势[7-8]。文献[7]将禁忌搜索与遗传算法配合,在利用遗传算法求解配送中心选址问题的同时,设计禁忌搜索规则来解决配送中心选址所涉及的路线安排问题。文献[8]研究了模拟退火算法与遗传算法融合的混合遗传方式,有一定的指导意义,但是在实际应用实现中还需针对问题具体分析。
本文设计了一种基于PS(predatory search)的改进遗传算法,来提高算法的综合搜索能力,并进一步研究了基于改进遗传算法的飞行器航迹规划问题。
1 GA简介
GA是根据生物的进化思想启发而得出的一种全局优化算法,通过对生物遗传和进化过程中选择、交叉、变异机理的模仿,来完成对问题最优解的自适应搜索过程。GA主要执行以下步骤[9]:
(1) 依据编码方式生成初始种群
编码是GA要解决的首要问题,通过编码将解空间的数据表示成基因串数据,按照相应的编码方案随机产生指定种群大小的个体。
(2) 适应度分配
GA在搜索过程中用适应度来评估个体的优劣,并作为后续遗传操作的依据,个体的适应度越大则被遗传到下一代的概率就越大。
(3) 选择操作
选择操作是根据各个个体的适应度值,按照“适者生存”的规则,从上一代群体中选择出一些优良的个体遗传到下一代群体中。GA进行选择的原则是适应性强的个体为下一代贡献的概率大,则被保留到下一代的概率也大。
(4) 交叉操作
交叉操作是GA最主要的遗传操作,通过交叉操作可以得到新一代个体,新个体组合了父辈个体的特性。简单的交叉操作是按照交叉概率随机选择若干对染色体并随机选取交叉点实行相应位置的基因交换,得到新的染色体。
(5) 变异操作
变异操作是对于群体中的任一个体,以一定的概率随机改变串结构中某个串的值,即对群体中的个体,以某一概率改变某一个或一些基因座上的基因值。
(6) 重插入操作
通过以上遗传环节所生成的子代个体,通过基于适应度的再选择机制被保留并插入父代种群中,同时父代中相应位置的个体被淘汰,从而产生新的参与下一代进化的种群。
2 PSGA算法的实现
2.1 PSGA算法的改进方法
本文设计一种基于PS[10-12]的改进遗传算法。主要基于2个理由:① GA的收敛主要取决于交叉算子和变异算子,交叉算子提供了全局搜索能力,而变异算子则提供了局部搜索能力。进化初期,应确保种群在大范围内搜索,进行全局进化以避免过早收敛;进化后期,种群成熟度较高,个体更加逼近最优解,种群应该在局部范围内搜索,尽可能提高搜索精度[10]。因此,交叉概率和变异概率的取值需综合考虑,平衡选择。② PS是一种模拟动物捕食行为的空间搜索策略[11],能够有效地平衡全局探索能力和局部开发能力。PS的基本思想是:动物在捕食过程中,当没有发现猎物或猎物迹象时,在整个捕食空间沿着一定的方向以很快的速度寻找猎物;一旦发现猎物或发现猎物迹象,它们就放慢步伐,在发现猎物或存在猎物迹象的区域进行集中搜索,以期望找到猎物;如果寻找一段时间后而没有找到猎物,捕食动物将放弃这种集中的区域,而继续在整个捕食空间寻找猎物。
借鉴PS思想,改进的PSGA(predatory search genetic algorithms)算法采取以下原理:算法运行时,首先以较大的交叉概率Pc1和较小的变异概率Pm1进行全局搜索;一旦发现一个较好的解,则改变为以较大的变异概率Pc2和较小的交叉概率Pm2进行局部搜索;如果在局部搜索过程中最优解得不到改善,则再以较大的交叉概率Pc1和较小的变异概率Pm1进行全局探索。在整个算法运行过程中,不断地根据搜索解的情况自适应地调整交叉概率和变异概率的取值。
本文设计的PSGA算法的具体方法为:在进化过程中,根据适应度的变化来调整交叉和变异概率,以平衡全局搜索和局部开发。以最小化适应度为目标,设历代最好适应度为gbest,当代最好适应度为fbest,以两者的比值g=fbest/gbest来改变交叉和变异概率。设定一个小于1的正数k,比较g值和k值的大小,如果g≤k,则进行局部开发,优化代数为num代,交叉概率和变异概率分别取为Pc2和Pm2;如果g>k,则以Pc1和Pm1来更新交叉和变异概率。
这里k的取值对PSGA算法的性能有较大的影响,k可以取常量,也可以取变量。当k取常量时,若k值取得过大,则使得不同代数个体间的最优适应度值差异不明显时就进行局部寻优,可能会围绕一些非较优解进行局部搜索,从而影响算法的全局搜索性能;若k值取得过小,则使得不同代数个体间的最优适应度值具有较大差异时才进行局部寻优,可能会忽略掉进化过程中搜索到的一些较优解,从而影响算法的局部搜索性能。当k取变量时,考虑到遗传算法在进化过程中,进化初期个体的差异性较大,不同个体间适应度值的差异相应较大,进化后期个体的差异性较小,不同个体间适应度值的差异也相应较小,因此k的值可以根据进化代数的增加逐渐递增。
对于Pc1和Pm1的取值,采用自适应交叉和变异,Pc1和Pm1将随着进化代数动态地改变。
Pc1=Pc1_max-(Pc1_max-Pc1_min)i/M,
Pm1=Pm1_min+(Pm1_max-Pm1_min)i/M,
(1)
式中:i为进化代数;M为总进化代数;Pc1_max,Pc1_min分别为最大、最小交叉概率;Pm1_max,Pm1_min分别为最大、最小变异概率。
对于Pc2和Pm2的取值,采取式(2)的方法:
Pc2=P0g,
Pm2=P1/g,
(2)
式中:P0,P1为固定值。
对于num的取值,采取方法为
num=「n/g⎤,
(3)
式中:“「·⎤”表示向上取整函数,如「3.4⎤=4;n为固定值。
改进的PSGA算法的具体步骤如下:
(1) 初始化种群,根据式(1)对交叉概率Pc1和变异概率Pm1取值。
(2) 计算种群中个体的适应度,并根据本代最佳适应度和历代最佳适应度的比值g确定交叉和变异概率。如果g≤k,则根据式(2)进行局部优化num代;否则以Pc1和Pm1更新交叉和变异概率进行进化。
(3) 选择。根据个体适应度的大小按轮盘赌方法选择个体,并采用精英保留策略保留最优个体。
(4) 交叉。随机配对交叉产生新个体。
(5) 变异。对种群中个体进行变异。
(6) 进化终止条件判断,如满足条件,则停止计算,输出最佳结果;否则,执行(2)。
2.2 仿真测试
(1) 测试函数
对本文改进的PSGA算法的仿真测试采用2个经典函数,分别为一元多极值函数f1和多元多峰函数f2(Shubert函数)。
f1:f(x)=xsin(12πx)+2.0,x∈[-3.54],
(4)
(5)
式中:f1为周期震荡函数,在当前限定域中,当x=3.958 5时取得极小值-1.958 4;f2为一个多峰值多极值函数,在其定义域内总共有760个局部最小点,其中有18个是全局最小点,全局最小值为13.269 1。
(2)k值的确定
本文改进的PSGA算法对k的取值分为3种情况进行测试:k=0.8,k=0.99,k=0.8+0.19i/M,i为进化代数,M为总进化代数。测试结果如表1所示。表1中,算法的种群规模为80,针对每个函数,在每个k值和不同的最大设定代数情况下分别运行30次。收敛是指算法终止时,优化结果与理论最优值之间的误差在0.001以内。
从表1可以看出:k取3种不同的值,当运行代数超过100代时,针对2个函数f1和f2,算法均收敛到理论最优解,显示该算法具有较强的寻优能力。当运行代数为50代时,对f1,k=0.8和k=0.99时算法收敛性能稍好;对f2,k=0.8+0.19i/M时算法收敛性能稍好。可见k值的选择要根据具体情况来确定。考虑到航迹规划目标函数是一个复杂多极值函数,本文根据k=0.8+0.19i/M取值。
(3) 不同算法的比较
为了说明改进的PSGA算法的搜索性能,现将改进的PSGA算法与其他一些算法进行仿真测试比较,参与对比测试的算法为:基本遗传算法(SGA)、自适应遗传算法(AGA)及本文的PSGA算法。遗传操作方式采取单点交叉和基本位变异。
GA算法中Pc=0.7,Pm=0.05。
AGA算法中自适应概率调整为
(6)
式中:fmax为种群中最大的适应度值;favg为每代种群的平均适应度值;f′为要交叉的2个个体中较小的适应度值;f为要变异个体的适应度值;Pc1=0.85;Pc2=0.5;Pm1=0.06;Pm2=0.03。
PSGA算法中,Pc1_max=0.85,Pc1_min=0.5,Pm1_max=0.06,Pm1_min=0.03,另P0=0.3,P1=0.06,n=5,k=0.8+0.19i/M。
仿真测试时,各算法的种群规模均为80,每个算法分别在不同的最大迭代代数设置下运行30次。测试的所有数据和结果都在同一计算环境上(即同一台计算机、同一个操作系统和同一段时间内)运算所得。表2表示各算法针对不同的最大迭代代数设置分别运行30次的数据统计结果。
从表2中可以看出:
(1) 对函数f1,f2测试的结果数据中,最大迭代代数为50代时,PSGA算法稍不如AGA,主要原因是PSGA算法在发现较好解之后要进行局部搜索,由此降低了交叉概率,从而使种群中产生较好新个体的可能性变小,这在一定程度上影响了算法的收敛速度。尤其在进化早期,对算法的影响较大。
(2) 最大迭代代数设置为100,200,300代时,无论从平均适应度值、收敛次数,还是收敛到理论最优值的次数,PSGA算法均略优于GA,AGA,表明随着迭代代数的增加,PSGA算法具有更高的收敛精度和收敛率,这说明PSGA算法在提高算法的搜索精度和防止陷入局部最优方面起到了很好的效果。
(3) 从表2的平均运行时间比较来看,对于算法的改进带来程序在执行效率上的略微降低,但是,相对于达成优化目标而言,这种损失是必然的和可以接受的。

表1 PSGA算法在不同k值和不同进化代数下的测试结果Table 1 Test results for PSGA algorithm in different k values and different evolution algebras
3 PSGA算法在岸基导弹火力分配中的应用
3.1 火力分配模型
对导弹火力分配问题的解决一般假设[13]:红方有k种导弹的发射平台,而且每种发射平台只发射某一型导弹;打击目标有n个,目标重要程度为Wj,j=1,2,…,n,可用表达式Wj=(a1,a2)(sj,wj)T来表示,其中sj表示目标j的价值因素,wj表示目标j的威胁度,a1,a2为权重系数,0 (7) 式中:xij为第i种发射平台用于打击第j个目标的导弹数目。 此问题的模型可描述为:寻找问题一组解X,满足以下目标函数与约束条件,目标函数为 (8) 约束条件为 (9) 毁伤概率Pij可表示为[14] i=1,2,…,n,j=1,2,…,m, (10) 故构建舰艇毁伤效益最优火力分配模型为 (11) 约束条件为 3.2.1 战场想定 岸导部队接上级指挥机关命令,对蓝方某具有重要战略意义的岛屿实施海上封锁。岸导部队通过合理选择发射阵地,可使封锁海域处于其火力打击范围之内。 据上级情报:蓝方一海上护航运输船编队试图借助高海情的掩护,对该岛屿实施装备物资保障(其中2艘均可发射箔条弹和释放电磁干扰的运输船,3艘均装备有防空武器和电磁干扰设备的护卫舰)。 考虑到特殊战场条件下,舰艇不便出航、飞机不便出动的特殊情况,红方岸导部队独立遂行打击该编队的任务,破坏蓝方作战企图。作战岸导部队编制为1个团,下辖2个营。假设红方信息渠道通畅,部队已机动到达某预设阵地待机,随时等待发射命令。战场敌我态势如图1所示。 图1 战场态势图Fig.1 Battlefield situation 各参数取值如下: (1) 综合考虑运输船A,B,护卫舰C,D,E的政治价值、军事价值和经济价值得到其综合价值分别为0.8,0.7,0.4,0.3,0.3。 (2) 根据作战主要目的(对运输船进行打击),通过层次分析法对舰艇综合价值和威胁度的权重进行归一化处理后得到a1为0.7,a2为0.3。 (3) 参数数值 查阅导弹相关数据,并由有关公式计算得参数数值如表3所示。 表3 参数数值表Table 3 Numerical value of parameters (4) 红方岸导团对蓝方运输船编队实施集火打击,由于新型岸舰导弹连续发射时间间隔小于4.5 s,经过合理的航路规划后,可以使48枚导弹同时从不同方向打击敌编队。 (5) 蓝方编队采取独立防御措施,每艘舰艇独立完成防御任务。舰艇之间的间距合理,1枚导弹不会同时击伤2艘舰艇。 (6) 蓝方舰船的弹药数量没有限制,即只要其没有被消灭,就可以一直对来袭导弹进行拦截。 (7) 蓝方战场信息资源丰富,可以有效地对红方导弹进行不同程度地拦截。 (8) 红方战区信息保障充分,岸导部队发射阵地在战区防空火力范围内能获得有效的信息保障。 3.2.2 仿真计算与分析 根据模型(11),采用遗传算法进行仿真。仿真条件为:Matlab7.1,CPU Pentium 1.6G 内存2G。仿真得到火力分配方案如表4所示。 表4 火力分配方案Table 4 Fire distribution scheme 导弹发射总数为43枚。其中21枚导弹对运输船A,B进行了打击,由于A,B的价值差异,较多的导弹(12枚)射向了价值较大的A船;另有22枚导弹对护卫舰C,D,E进行了打击,由于护卫舰C的威胁度较高,但同时C舰的拦截概率也较高,导致导弹在3个目标间的分配数目差别不大(仅为1枚)。对各目标的毁伤概率依次为:0.96,0.95,0.84,0.87,0.87,对目标的毁伤程度均为击毁。结果符合作战要求。 从仿真结果可以看出: (1) 分配方案证明了模型的有效性 分配方案符合作战要求。其中在打击运输船编队任务中,主要作战目的是对运输船进行打击。由于2艘运输船A,B的综合价值分别为0.8,0.7,分配方案中打击A船的导弹数目多于B船,在相同威胁度和射击有利度条件下,导弹分配偏向了价值大的运输船。 在3艘护卫舰C,D,E中,C舰综合价值高于D舰和E舰(综合价值依次为0.4,0.3,0.3)。在威胁度方面,C舰高于D舰,D舰高于E舰(威胁度依次为0.6,0.55,0.5)。因此在射击有利度差别不大的情况下,导弹在3个目标间的分配数目差别不大。 (2) 分配方案反映了模型特点 极大化毁伤效益模型偏重对目标的毁伤效益。如果拥有导弹数目较充裕,其所得分配方案发射弹数目很大(43枚),作战消耗较大。如果没有对某一目标进行集火射击的导弹数目0≤xj≤12,j=1,2,…,5这一约束,其结果必然是发射所有导弹以求得最大的效益。 (3) 权重系数的选择更有利于达成作战意图 考虑到主要作战目的是对运输船A,B实施火力打击,而运输船的威胁度相对护卫舰有一定差距,为了使分配方案符合作战意图,利用层次分析法将舰艇综合价值sj和威胁度wj系数进行归一化处理后设定各自权重为:0.7,0.3。因此威胁度的“地位”相对舰艇价值有所降低,即岸舰导弹火力分配方案在2个参数间进行决策时将偏重于舰艇综合价值这一参数的大小。如果没有权系数的引入,那么威胁度与舰艇综合价值地位“平等”,分配方案必然倾向于护卫舰。即:在相同的毁伤概率条件下,护卫舰C的价值和威胁度乘积明显高于运输船A,分配方案必然偏重于护卫舰C。根据首长要求和作战意图,合理地确定和调整权重系数,对导弹火力分配方案有明显影响。 本文将动物捕食思想引入遗传算法,设计了一种基于捕食策略的改进遗传算法,通过实例测试表明,该算法与基本遗传算法、自适应遗传算法相比具有更好的综合搜索能力。进一步研究了基于改进遗传算法的岸基导弹对海上舰艇目标攻击时的火力分配问题,构建了火力分配模型,通过仿真实验验证了模型及算法的有效性。 参考文献: [1] SZCZERBA R J,GALKOWSKI P G,LICKSTIN I S,et al.Robust Algorithm for Real-Time Route Planning[J].IEEE Transactions on Aerospace and Electronic Systems,2000,36(3):869-878. [2] 姚毅.基于遗传算法的战斗机低空突防航路规划研究[D].武汉:海军工程大学,2007. YAO Yi.Low-Altitude Penetration Path Planning Based on Genetic Algorithm[D]. Wuhan:Naval University of engineering, 2007 [3] 袁麟博,章卫国,李广文.一种基于遗传算法-模式搜索法的无人机路径规划[J].弹箭与制导学报,2009,29(3):279-282. YUAN Lin-bo, ZHANG Wei-guo, Li Guang-wen.A UAV Path Planning Based on Genetic Algorithm-Pattern Searching[J].Journal of Missiles and Guidance, 2009,29(3): 279-282. [4] 马云红,周德云.一种无人机路径规划的混沌遗传算法[J].西北工业大学学报,2006,24(4): 468-471. MA Yun-hong, ZHOU De-yun. A UAV Path Planning Based on Chaos Genetic Algorithm[J]. Journal of Northwestern Polytechnical University, 2006,24(4): 468-471. [5] 雷英杰,张善文,李继武,等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005. LEI Ying-jie, ZHANG Shan-wen, LI Ji-wu ,et al. Genetic Algorithm Toolbox and Its Application in MATLAB [M]. Xi’an: Xi’an Electronic and Science University Press, 2005. [6] BAGLEY J D.The Behavior of Adaptive Systerm which Employ Genetic and Correlation Algorithm[J].Dissertation Abstricts International,1967,28(12):78-90. [7] 胡大伟,陈诚.遗传算法和禁忌搜索算法在配送中心选址和路线问题中的应用[J].系统工程理论与实践,2007,9(9):171-176. HU Da-wei, CHEN Cheng. Application of Genetic Algorithm and Tabu Search Algorithm in Distribution Center Location and Routing Problems[J].Systems Engineering Theory and Practice, 2007,9(9): 171-176. [8] 王雪梅,王义和.模拟退火法与遗传算法的结合[J].计算机学报,1997,20(4):381-384. WANG Xue-mei, WANG Yi-he.Combining Simulated Annealing Algorithm with Genetic Algorithm[J].Chinese Journal of Computers, 1997,20(4): 381-384. [9] 明亮.遗传算法的模式理论及收敛理论[D].西安:西安电子科技大学,2006. MING Liang.Schema Theory and Convergence Theory of Genetic Algorithm[D]. Xi'an: Xi'an Electronic and Science University, 2006. [10] 张顶学,关治洪,刘新芝.基于捕食搜索策略的遗传算法研究[J].计算机应用研究,2008,25(4): 1006-1007. ZHANG Ding-xue,GUANG Zhi-hong,LIU Xin-zhi.Research on Genetic Algorithm of Predatory Search Strategy [J].Computer Application Research,2008,25(4): 1006-1007. [11] LINHARES A.Preying on Optima:a Predatory Search Strategy for Combinatorial Problems[C]∥Proc of IEEE International Conference of Systems,Man and Cybernetics.Piscataway NJ, 1998: 2974-2978. [12] LINHARES A.Synthesizing a Predatory Search Strategy for VLSI Layouts[J].IEEE Tran.On Evolutionary Computation,1999,3(2):147-152. [13] 冯杰.遗传算法及其在导弹火力分配上的应用[J].火力与指挥控制,2004,29(2):43-45. FENG Jie.Genetic Algorithm and Its Application in Missile Fire Allocation[J].Fire Control and Command System,2004,29(2): 43-45. [14] 杨飞,董朝阳. 实施饱和攻击的反舰导弹武器火力分配[J].系统仿真学报,2011,23(2):316-320. YANG Fei,DONG Zhao-yang.The Fire Allocation in Saturation Attack for Anti-Ship Missile[J].Journal of System Simulation,2011,23(2):316-320. [15] 胡正东,丁洪波. 反舰导弹武器系统的火力分配方法研究[J].战术导弹技术,2008,6(2):1-3. HU Zheng-dong, DING Hong-bo.The Allocation Methods of Anti-Ship Missile Weapon System[J].Tactical Missile Technology,2008,6(2):1-3. [16] 尤大德,徐德民.水面舰艇防空武器抗击单枚反舰导弹的效能评估[J]. 火力与指挥控制,2010,16(10):81-83. YOU Da-de, XU De-min.Effectiveness Evaluation of Warship Air Defense Weapons Against Single Anti-Ship Missile[J]. Fire Control and Command,2010,16(10):81-83.


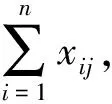
3.2 仿真算例



4 结束语
