改进CHNN神经网络航迹关联算法*

柏慧风，高贵明

(1.南京信息工程大学 电子与信息工程学院,江苏 南京 210044;2.南京船舶雷达研究所,江苏 南京 210003)

0 引言

多传感器数据融合技术将来自多个传感器的数据进行组合，其结果将比单个传感器系统得到的结果具有更高的性能和精确度[1]。在多传感器多目标跟踪系统中主要有2种形式的数据关联[2]。一种是点迹与航迹的关联，另一种是航迹和航迹的关联。航迹关联时，基于统计的航迹关联算法[3]，将不同传感器测得的航迹送往数据融合中心进行处理，以确定是否有2条或更多条航迹来自于同一个目标。但是在目标密集或者航迹交叉的情形下，某些航迹彼此之间距离较近，此时进行航迹关联难度较大，存在增大错误关联概率的可能。独立序贯法[4]能够应对密集目标及航迹交叉的情况，但是该算法需要消耗大量计算时间，实时性得不到保证。还有很多针对多传感器多目标跟踪融合系统的其他算法也得到了人们的研究，比如多维分配算法[5]，遗传算法[6]等。这些算法的主要思想是将航迹关联问题转换为组合优化问题，而组合优化问题本身就是一个难以解决的问题。由于神经网络技术对优化问题固有的并行计算的能力，基于Hopfield神经网络[7-9]的算法也得到了发展。

本文首先介绍连续型Hopfield神经网络(continuous state hopfield neural network,CHNN)技术[10-11]以及基于此技术而提出的算法。但是，该算法有一个缺点：仅仅适用于每个传感器都发现了相同的目标，即采用该算法的前提是不同传感器测得的航迹来自于相同数目的相同目标。而实际情况却不能满足这种条件。于是本文将该算法进行改进：对某些传感器引入伪航迹，这样，不同传感器测得的航迹间马氏距离就可以从3个状态进行定义。根据以上处理，针对不同传感器的航迹可以建立一个能量函数。因此，通过对神经网络应用能量函数可以获得神经元的连接权重和阈值。于是航迹关联问题就可以用神经网络技术来解决。当神经网络收敛之后，神经元的输出就是航迹关联的结果，并且可以通过重新定义统计量来加速神经网络的收敛，从而减少关联时间，提高实时性。

1 CHNN算法

定义运动目标的状态空间模型:

X(k+1)=F(k)X(k)+G(k)W(k)+U(k),

(1)

Y(k)=H(k)X(K)+V(k),

(2)

式中：X(k)为目标的状态向量；Y(k)为观测向量；F(k)为状态转移矩阵；H(k)为观测矩阵；G(k)为噪声增益矩阵；U(k)为强制输入；W(k)为系统噪声，一般均值为0；V(k)为测量噪声，其均值一般为0，并且和系统噪声不相关。

(3)

Cj,l(k)=Pj(k)+Pl(k).

(4)

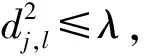
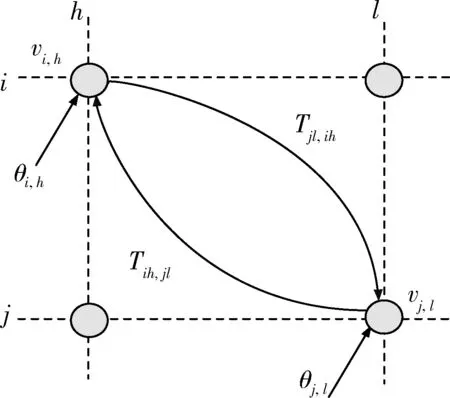
图1 神经网络示意图Fig.1 Diagrammatic sketch of neural network

在Hopfield神经网络关联中，用vj,l代表传感器A的第j条航迹和传感器B的第k航迹的关联状态，其值为1时，表示2条航迹关联，其值为0时表示2条航迹不关联。连续型Hopfield神经网络的动态方程为[12]

(5)

用于航迹关联的能量函数定义为

(6)

式中:dj,l(k)为等式(3)定义的马氏距离；第1、第2、第3项约束表示一个传感器的每一条航迹有且仅有其他传感器的一条航迹关联。合理设置参数，神经元的状态就会给出航迹关联结果。

2 改进CHNN算法

实际应用当中，并不是一个传感器的每一条航迹有且仅有另一个传感器的一条航迹关联。一般来说，传感器A和传感器B分别测得N和M个目标。为了解决这种情形下的航迹关联问题，可以将传感器A的所有航迹作为伪航迹加入到传感器B中，即j∈1,2，...，Nandl∈1,2，...，N,N+1,...N+M是传感器B的航迹索引。此时传感器A的第j条航迹和传感器B的第l条航迹的马氏距离修正为

(7)

式中：λj比统计算法中的统计门限稍大。

(1) 2个传感器航迹关联

根据以上处理，航迹关联问题可以映射为拥有N×(N+M)个神经元的神经网络问题。此处能量函数定义为

(8)

式中：第1项确保每一列至多有一个神经元关联上；第2项表示每一行有且仅有一个神经元关联上；第3项表示关联上的航迹间马氏距离之和；第4项用来加快神经网络的收敛速度。

(2) 多个传感器航迹关联

当系统中拥有3个传感器的航迹需要航迹关联时，假设传感器A，B，C分别测得N,M,S条航迹，将伪航迹分别引入，传感器B、传感器C，得到传感器A，B，C的新的航迹索引为：j∈1,2，…，N；l∈1,2，…，N,…，N+M；m∈1,2，…，N,…，N+M,…，N+M+S。

新的统计量定义为

bj,l,m(k)=Dj,l(k)+Dl,m(k).

(9)

这样，航迹关联问题可以映射为拥有N×(N+M)×(N+M+S)个神经元的神经网络问题来求解，此时，连续型Hopfield神经网络的动态方程为

(10)

类似等式(8)，此时3个传感器的能量函数定义为

(11)

由于引入了伪航迹，神经网络问题的规模在不断扩大，为了改进神经网络性能，将传感器A的第j条航迹与传感器B的第l条航迹的马氏距离修正为

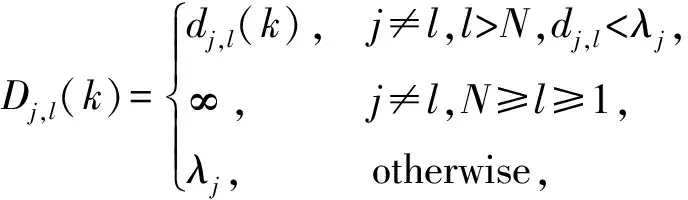
(12)

式中：λj比统计算法中的统计门限稍大。

通过以上处理，将有大量统计量bj,l,m(k)趋于无穷大，这样使不可能关联的航迹对应的神经元处于正确的状态，加快了神经网络的收敛速度。同理，当传感器的数目大于3个时，采用的方法相类似。

3 计算机仿真

为了验证该改进算法的有效性，模拟几条航路，包括直线、曲线运动等5个目标。目标1的初始位置为(0,120 000,120 000 )m，以(300,300,300 )m/s的速度匀速直线运动；目标2初始位置(0,120 000,45 000 )m，0～150 s沿z平面作45°转弯运动，150～200 s作角度为135°慢转弯，加速度为(7.5,1.5,0 )m/s2，完成慢转弯后加速度将为0，200～400 s作速度为(120,120,100 )m/s的匀速直线运动；目标3初始位置为(0,115 000,0 )m，0～150 s采用3个模型的交互多模型(IMM)算法，设定各模型在此时刻的概率分别为(0.8,0.1,0.1)，150～400 s作角度为30°的慢转弯；目标4的初始位置为(0,0,140 000 )m,以(50,0,-350 )m/s的速度匀速直线运动；目标5初始位置是(0,0,0 )m，0～50 s以(0,0,80 )m/s的速度直线运动，51～200 s以(60,70,80 ) m/s速度直线运动，200～400 s以(100,100,60)m/s的速度直线运动。采用4个传感器进行目标跟踪，得到的航迹如图2所示。进一步地，为了体现目标密集的情形，采用4个传感器跟踪25个目标，这25条航迹要有大量交叉航迹，且彼此之间航迹相距较近。针对以上6个目标和25个目标的情形，分别给出采用本文改进的算法进行航迹关联，得到的航迹关联概率如图3所示。

图2 多传感器多目标跟踪Fig.2 Multi-sensor multi-target tracking

图3 2种情况航迹正确关联概率Fig.3 True association probability of two situation

由图3可知，在目标密集的情况下，利用本文的改进算法依然可以得到将近90%的正确关联概率。引入伪航迹后，由于式(8)中第(4)项可以加快神经网络的收敛速度，利用仿真进行算法收敛性的时间比较如表1。

表1 算法收敛比较Table 1 Comparison of the convergence

4 结论语

本文提出了一种改进的基于CHNN的航迹关联算法。通过重新定义统计量马氏距离来改进神经网络的关联性能。从结果可以看出，改进的航迹关联算法具有很好的航迹关联效果，并且适用于3个甚至更多传感器的航迹关联，在保证关联质量的同时，大大地扩展了使用范围。同时，改进的算法同样适用于密集目标和航迹交叉的情况。

参考文献：

[1] LINAS J,HALL D. An Introduction to Multisensor Data Fusion[J]. Proceedings of the IEEE International Symposium on Circuit and System, 1998, 6(5)： 537-540.

[2] BAR-SHALOM Y,FORTMAN T. Tracking and Data Association[M]. New York：Academic Press, 1988：81-83.

[3] 韩崇昭，朱红艳，段战胜,等. 多源信息融合[M].北京：清华大学出版社, 2006：95-97.

HAN Sui-zhao, ZHU Hong-yan, DUAN Zhan，et al. Multi Information Fusion[M].Beijing:Tsinghua University press, 2006: 95-97.

[4] BAR-SHALOM Y,LI X R. Multitarget-Multisensor Tracking: Principles and Techniques Stors [J].YBS Publishing 1995,2(2):73-74.

[5] BLAIR W D, RICE T R. Asynchronous. Data Fusion For Tracking With a Multitasking Radar and Optical Sensor [J]. SPIE ,1991，5(4):234-245.

[6] 何友，田保国. 基于神经网络的广义经典分配航迹关联算法[J]. 航空学报，2004，25(3):300-303.

HE You, TIAN Bao-guo. Generalized Classical Assignment of Track Correlation Algorithm Based on Neural Network[J]. Chinese Journal of Aeronautics, 2004，25(3):300-303.

[7] TIAN Bao-guo, HE You, YANG Ri-jie. Application of Artificaial Neural Network in Track Correlation[J]. Journal of Electronics & Information Technology, 2005,27(2):116-202.

[8] HE You, TIAN Bao-Guo. Application of Neural Network in Track Correlation of Distributed Multisensor Systems[J]. Acta Aeronautica et Astronautica Sinica,2004,25(3):1126-1130.

[9] 田宝国，陈建. 基于神经网络的多传感器模糊航迹关联算法[J].舰船电子工程，2009，29(11):132-136.

TIAN Bao-guo, CHEN Jian. Multi-Sensor Fuzzy Track Association Based on Neural Network Algorthm[J]. Ship Electronic Engineering, 2009，29(11):132-136.

[10] HE Bao-lin, MAO Zheng, LIU Yuan-yuan, et al . A Generalized CHNN Method for Track-to-Track Association[J]. The Ninth International Conference on Electronic Measurement & Instruments, 2009,23(4):636-640.

[11] TAN KC, TANG Hua-jin. On Parameter Settings of Hopfield Networks Applied to Traveling Salesman Problems[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers, 2005,5(5):517-527.

[12] CHEN Xiao-hui, WAN De-jun. Study on Multisensor-Multitarget Tracking Using Neural Network[J].Journal of Southeast University:Natural Science Edition, 2003,33(4):269-275