基于滑动窗宽的非参数变宽直方图方法研究*
2014-07-10叶菲罗军高兴荣周杰
叶菲,罗军,高兴荣,周杰
(解放军陆军军官学院, 安徽 合肥 230031)
0 引言
雷达辐射源信号识别是雷达对抗的一个重要组成部分。实现雷达辐射源信号识别需要对雷达辐射源信号参数(如载频、脉冲重复周期、脉冲宽度、脉冲幅度等)进行特征提取与分析,通常采用统计直方图法[1-2]。统计直方图分组有等宽分组和不等宽分组。等宽分组直方图存在如下问题:靠近参数取值处的区间聚集大量的样本,而远离参数取值的区间却只包含少量甚至没有样本,使得直方图上部轮廓线与参数实际概率密度函数曲线不能很好地吻合,增加分组个数可以解决这个问题,但是以增加大量零样本区间为代价。不等宽分组可以解决这个问题,它可以根据参数的取值情况,选择不同的分组宽度[3]。
本文提出一种变宽直方图法,它通过对等宽直方图的区间进行合并或划分操作,使直方图上部轮廓线与参数概率密度函数曲线相吻合,从而确定出直方图的分组数。若参数的概率密度函数未知,则可以采用非参数概率密度估计方法预先进行估计[4-5]。
1 非参数变宽直方图算法
设T是某一实参数观测数据的集合,区间A是该参数的取值范围,将区间A划分为n个不相交的子集Ai,使其满足A=A1∪A2∪…∪An。对于一维数据集,直方图的横轴表示每一个子集的取值范围,纵轴表示数据位于该子集内上的频数。若各子区间宽度相等,就称为等宽直方图[6];各子区间宽度不相等,就称为变宽直方图。各子区间如何划分,也就是分组如何确定的问题是直方图算法中的关键问题[7]。
刘甸瑞教授[8-9]提出一种分组数确定方法。分组好坏总的评价准则是:分组要能使直方图最清晰地反映出数据可能服从的统计分布规律来。具体有以下3条准则:①分组后频数为0的组数不宜太多;②直方图上部的轮廓线应较为连续;③分数组不宜过多或过少。
基于上述准则,本文提出一种变宽直方图算法。为了满足准则①,可以将等宽直方图中频数较小的相邻区间进行合并;为了满足准则②,可以将等宽直方图中频数较大的区间进行划分,从而形成动态可变宽的直方图。图1中a)和b)分别为等宽直方图和变宽直方图,其中图1b)就是基于图1a)直方图调整变换而来。如图1所示。
将变宽直方图进行归一化处理,令归一化处理后直方图的上部轮廓线函数为f(x),如图2所示。
参数服从的概率密度函数为p(x),定义f(x)和p(x)的贴近度为
(1)
贴近度越小,说明直方图的上部轮廓线与参数概率密度函数越接近,此时的分组就越好;贴近度越大,说明直方图的上部轮廓线与参数概率密度函数相差较远,此时的分组就不是最优分组。

图1 2种直方图算法Fig.1 Two histogram algorithms
图2 直方图上部轮廓线示意图Fig.2 Figure of histogram upper contour
非参数变宽直方图算法采取自适应方法确定区间大小:首先用较大的区间长度构造等宽直方图,然后根据相邻区间内频数的差值大小来确定该区间是否需要划分及划分的程度,这种方法不仅可以降低计算量,而且可以得到更符合实际分布的直方图。设参数观测数据为xi(i=1,2,…,n),n代表该批观测数据的总个数,非参数变宽直方图算法具体步骤如下:
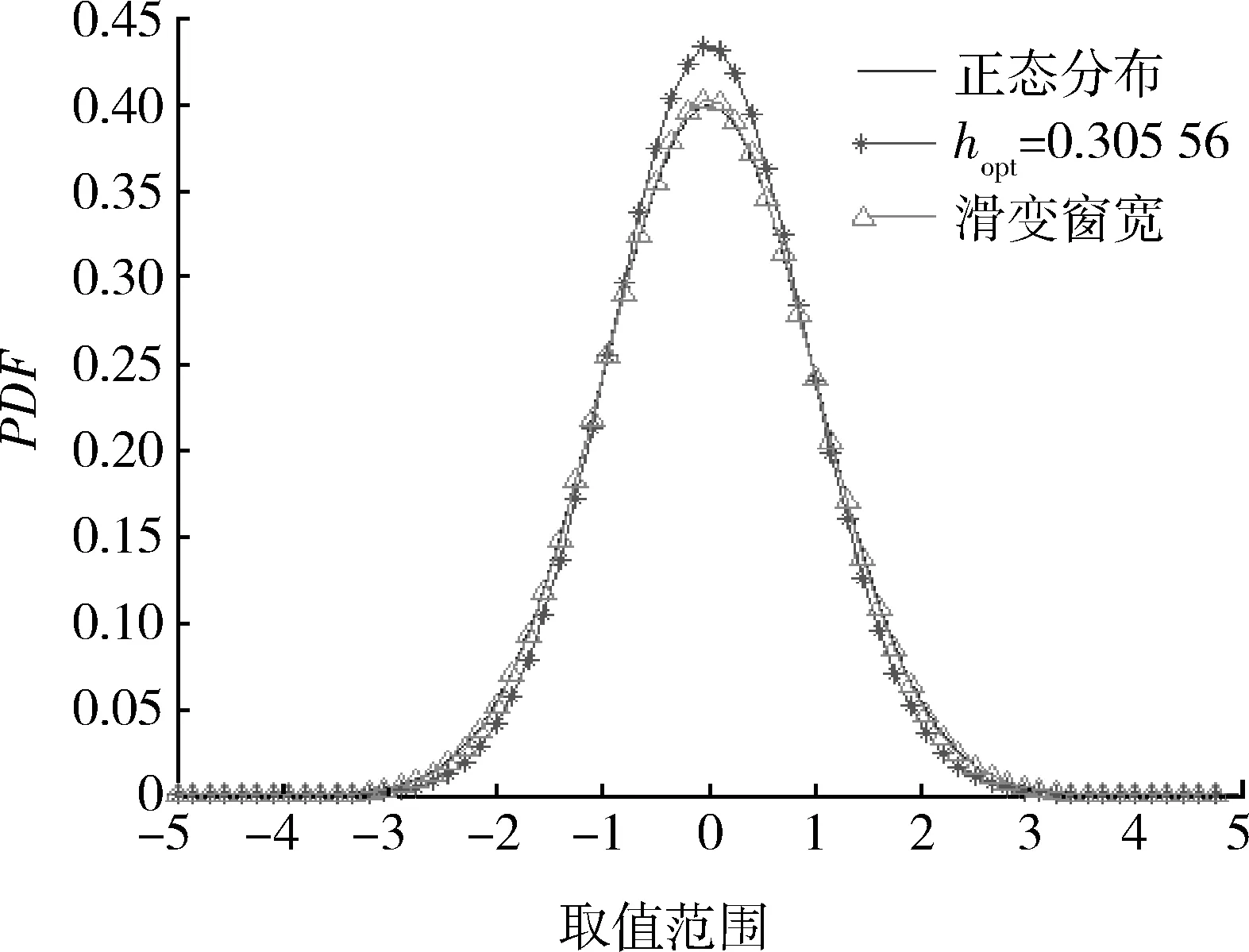
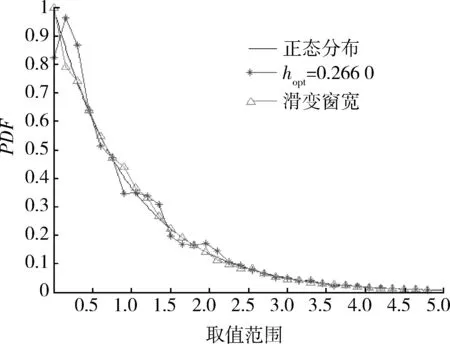
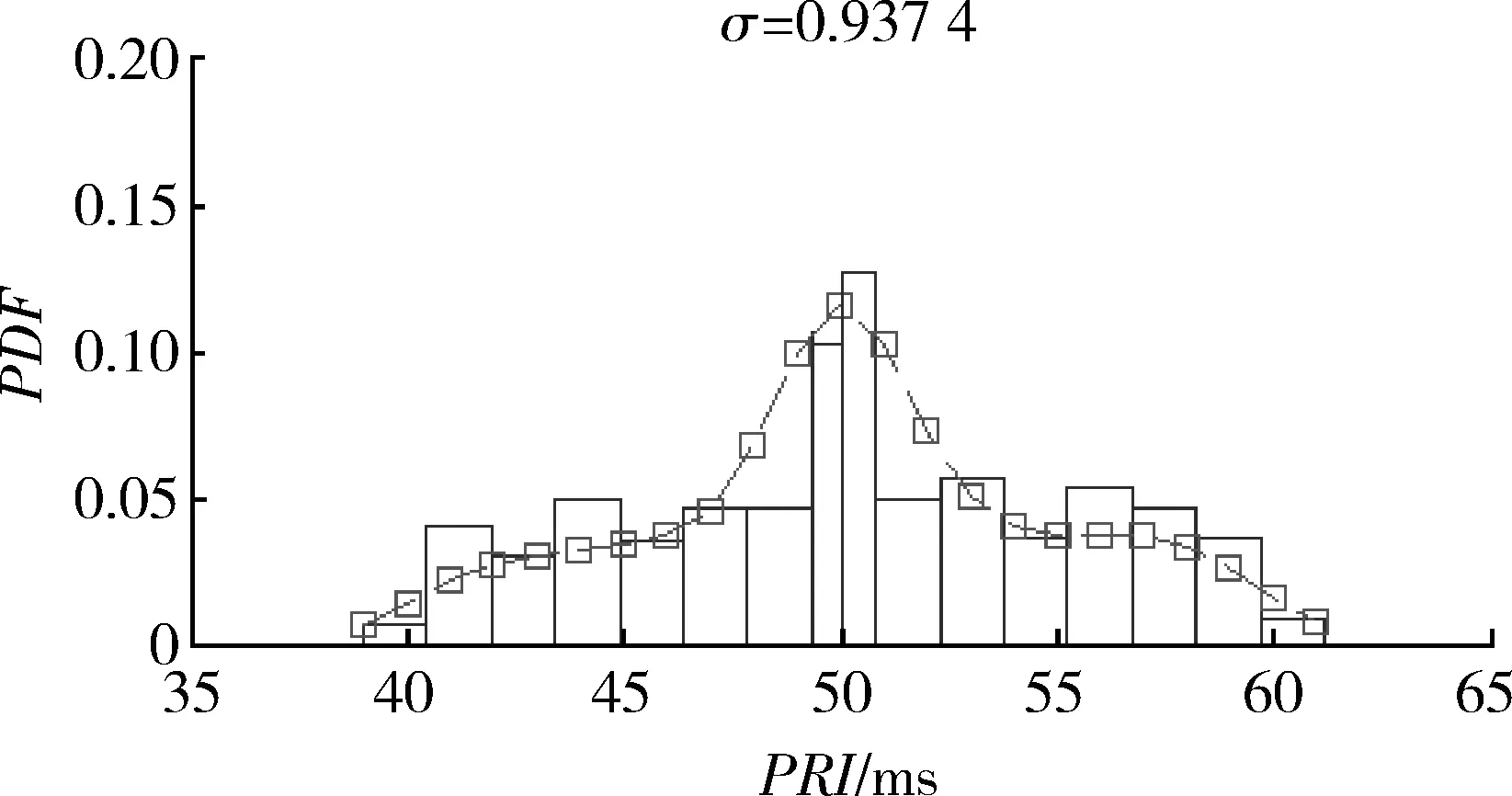
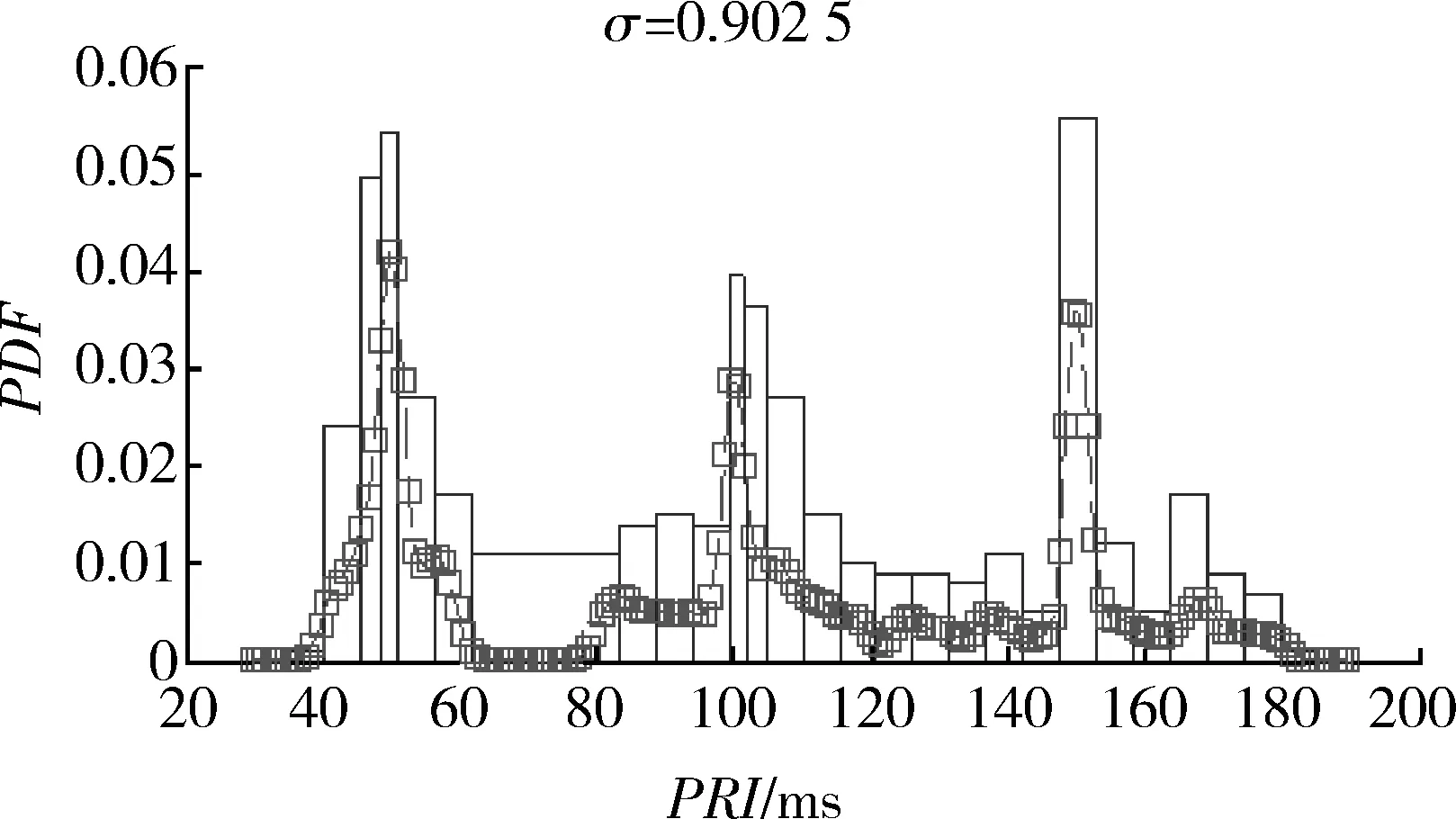
(3) 将[Xmin,Xmax]划分为M个大小相等且无交叠的区间Ai=[ai,ai+1),满足Xmin=a1<… (4) 计算在步骤(3)中设置的每一个区间中落入的样本个数fi(i=1,2,…,M)。 (5) 设定区间频数最大值fmax和最小值fmin。 (6) 若fi≤fmax,该区间不处理;反之对区间进行「fi/fmax⎤等份划分,「·⎤表示上式取整运算。记录新的区间序列Ai(i=1,2,…,N)和对应的区间频数fi(i=1,2,…,N)。 (7) 若fi>fmin,该区间不处理;反之,将该区间与频数较小的相邻区间进行合并,记录新的区间序列Ai(i=1,2,…,L)和对应的区间频数fi(i=1,2,…,L)。 设K(u)为定义在(-∞,∞)上的一个Borel可测函数,h>0为常数。 (2) 称为总体密度p(x)的一个核估计,h称为窗宽,K(u)称为核函数。核函数有方窗函数、正态窗函数和指数窗函数等,在大样本集情况下,核函数的选取对总体密度的估计并不是至关重要的,窗宽的选取才是核函数密度估计能否成功的关键[10]。最优窗宽的选择可以分为2类:固定窗宽算法和变窗宽算法。 固定窗宽算法假设真实密度p(x)服从N(u,σ2)分布,并使密度估计与真实密度之间的误差最小,可以得到优化的窗宽为[11-12] (3) 变窗宽算法也是从密度估计与真实密度之间的误差开始。但真实密度函数p(x)是未知的,否则就无需进行密度估计。一种处理方法与固定窗宽算法一样,假设一个真实密度。然而对于一个未知分布,通过核密度估计获得的密度函数,多数情况下,应该比一个假设的分布更加接近实际。因此,可以结合固定窗宽算法与变窗宽算法得到改进的非参数概率密度估计方法,具体步骤如下: (1) 根据式(3),计算固定最优窗宽hopt。 (4) 通过极小化MSE(h0),得到最优窗宽: (5) 从式(5)可以看出,h*(x)值与待求密度估计点x有关,其值随着估计点的不同而不同,利用式(2)求解x分布密度时,窗宽的取值随着x的变化而变化,变窗宽能够更好地反映估计区间不同点的光滑程度,降低拟合曲线在峰顶区域的偏差以及尾部区域的方差,提高拟合曲线的灵活性。 图3 正态分布曲线拟合结果Fig.3 Fitting result of normal distribution curve 图4 指数分布曲线拟合结果Fig.4 Fitting result of exponential distribution curve 实验2 为验证基于滑动窗宽非参数估计的变宽直方图算法的有效性,仿真一组固定类型的雷达辐射源信号基本参数脉冲重复周期(pulse repetition interval,PRI),取值为50 ms;仿真一组三参差类型的重复周期,取值分别为50,100,150 ms;。每种类型仿真500个样本,并设定1%的测量误差。在进行参数分析之前,利用滑动窗宽非参数估计方法估计出参数服从的概率密度函数,并设定贴近度门限σ=0.9。实验结果如图5和图6所示,基于直方图可以提取出参数值。再将仿真样本集测量误差改为5%,同样进行参数分析与特征提取,最终提取结果如表1所示。从表1可以看出,从直方图中获得到的数据取值情况与预设值是一致的,并且受误差的影响较小。因此基于滑动窗宽非参数估计的变宽直方图算法是有效的。 图5 固定PRI的概率密度曲线与变宽直方图Fig.5 PDF curve and variable-width histogram of fixed PRI 图6 三参差PRI的概率密度曲线与变宽直方图Fig.6 PDF curve and variable-width histogram of three-stagger PRI 表1 不同误差条件下参数提取结果 Table 1 Parameter extraction result in different errors 特征参数PRI1%误差5%误差固定类型预设值/ms5050提取值/ms50.34250.361参差类型预设值/ms50 100 15050 100 150提取值/ms51.484 100.691 150.32251.957 101.103 150.935 本文提出的变宽直方图算法通过对等宽直方图的区间进行合并或划分操作,使直方图上部轮廓线与参数概率密度函数曲线相吻合,以此作为分组数是否最优的判别依据。在参数概率密度未知的情况下,提出基于滑动窗宽的非参数概率算法预先估计出概率密度函数。滑动窗宽非参数概率估计将固定窗宽算法和变窗宽算法进行结合,实现窗宽根据样本的分布情况,在不同的估计点自动调整窗宽的取值。最后通过实验表明,本文提出的变宽直方图算法可以定量获得最优的分组数,在此过程中不需要人参与判断搜索过程是否结束,从而实现算法的自动化。 参考文献: [1] 陶荣辉, 李合生, 韩宇, 等. 基于直方图和小波网络的雷达信号识别方法[J]. 电波科学学报, 2005, 20(6): 784-788. TAO Rong-hui, LI He-sheng, HAN Yu, et al. A Novel Algorithm of Radar Signal Recognition Based on Histogram and Wavelet Network[J]. Chinese Journal of Radio Science, 2005, 20(6): 784-788. [2] 易波, 刘培国, 薛国义. 一种基于顺序差值直方图算法的改进雷达信号分选方法[J]. 舰船电子对抗, 2012, 35(1): 6-10. YI Bo, LIU Pei-guo, XUE Guo-yi. An Improved Method for Radar Signal Sorting Based on SDIF Histogram Algorithm[J]. Shipboard Electronic Countermeasure, 2012, 35(1): 6-10. [3] 李燕萍, 唐振民, 丁辉, 等. 基于非参数直方图模型的鲁棒说话人识别算法[J]. 数据采集与处理,2010, 21(1): 81-85. LI Yan-ping, TANG Zhen-min, DING Hui, et al. Novel Non-Parameter Model for Robust Speaker Precognition[J]. Journal of Data Acquisition & Processing, 2010, 21(1): 81-85. [4] 赵峰, 张军英, 刘敬, 等. 基于非参数化概率密度估计的雷达目标识别[J]. 电子与信息学报, 2008, 30(7): 1740-1743. ZHAO Feng, ZHANG Jun-ying, LIU Jing, et al. Radar Target Recognition Based on Nonparametric Density Estimation[J]. Journal of Electronics & Information Technology, 2008, 30(7): 1740-1743. [5] MALIK M I, AMIR A. Density Estimation and Random Variate Generation Using Multilayer Networks[J]. IEEE Trans. on. Neural Networks, 2002, 13(3): 497-520. [6] 陈婷, 罗景青. 基于直方图最优分组的雷达信号特征参数分析[J].微电子学与计算机, 2009, 26(3): 162-162. CHENG Ting, LUO Jing-qing.The Feature Parameter Analysis of Radar Signal Based on Best Grouping in Histogram[J]. Microelectronics & Computer, 2009, 26(3):162-165. [7] 姜旭宝, 李光耀, 连朔. 基于变宽直方图的无线传感器网络异常数据检测算法[J]. 计算机应用, 2011, 31(3): 694-697. JIANG Xu-bao, LI Guang-yao, LIAN Shuo. Outlier Detection Algorithm Based on Variable-Width Histogram for Wireless Sensor Network[J]. Journal of Computer Application, 2011,31(3): 694-697. [8] 刘甸瑞. 作直方图中的最优分组问题[J]. 物探化探计算技术, 1995, 17(1): 62-67. LIU Dian-rui. The Optimal Classification Problem in Constructing Histogram[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1995, 17(1):62-67. [9] 赵荣军. 直方图分组数的确定[J]. 物探化探计算技术, 1999, 21(1): 82-88. ZHAO Rong-jun. Solution for the Optimal Classification Numbers on Drawing Histogram[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1999, 21(1): 82-88. [10] SILVERMAN B W. Density Estimation for Statistics[M]. New York: Chapman and Hall,1986. [11] 于传强, 郭晓松, 张安, 等. 基于估计点的滑动窗宽核密度估计算法[J]. 兵工学报, 2009, 30(2):231-235. YU Chuan-qiang, GUO Xiao-song, ZHANG An, et al. Slide Bandwidth Kernel Density Estimation Algorithm Based on Estimate point[J]. Acta Armament Arii, 2009, 30(2): 231-235. [12] 邓飙, 于传强, 李天石, 等. 基于估计点的双窗宽核密度估计算法[J]. 仪器仪表学报,2011, 32(3): 615-620. DENG Biao, YU Chuan-qiang, LI Tian-shi, et al. Bual-Bandwidth Kernel Density Estimation Algorithm Based on Estimate Point[J]. Chinese Journal of Scientific Instrument, 2011, 32(3): 615-620.
2 改进的非参数概率密度估计方法


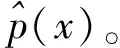
3 仿真实验



4 结束语
