Stratonovich积分和it积分探讨比较分析

冉 芳

(铁岭师范高等专科学校 辽宁铁岭 112000)

1 随机积分概述

1.1 布朗运动

1828年英国植物学家罗伯特·布朗在《哲学》杂志上发表论文，描述自己在显微镜下观察到的花粉粒在液体中不停运动，拉开了人了对于布朗运动认识的序幕．而后经过多名科学家的努力，证实了除了生命体细小的无机颗粒也存在着这种运动，从而将布朗运动从生物学引申到了物理学领域．

在物理学中，大多数物理现象使用微分方程来描述其模型，微分方程的建立是从导数的定义出发，根据微分和积分的关系，建立相应的积分方程．可是，随着物理学的发展，由于自然界的“不可预测”因素的出现，普通的微分方程已经无法满足相应的物理模型，所以需要新的微积分模型出现解决这一问题．

1.2 布朗运动的数学表述

对于布朗运动的数学表述，可以用连续可微的实值函数表述如下:

对于连续函数f(t)，考虑区间 ［0，T］的划分:

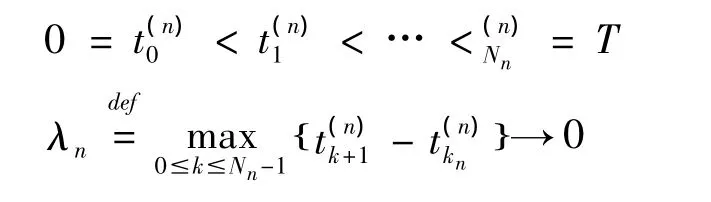
把f(t)的梯形近似函数写作fn(t)为:

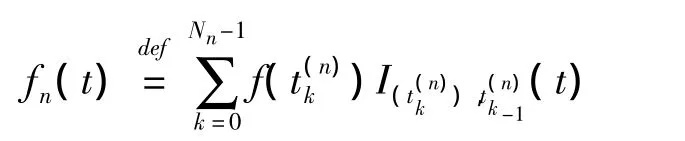
因此，可以定义如下积分和:

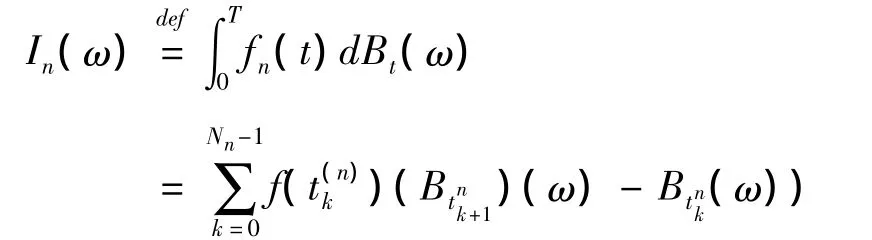
那么就有新的定义如果 (0，T］的子区间(si，ti］(i=1，2，…，m)两两不相交，则称

对于任意固定的ω，梯形函数对布朗运动的积分定义为:

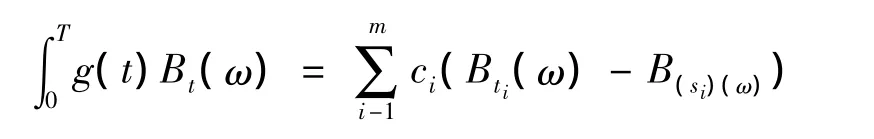
简单记做:

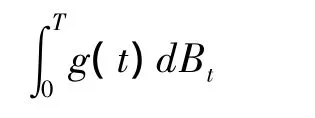
2 It积分

伊藤积分得名于日本数学家伊藤清，是将微积分概念扩展到随机过程中一种数学方法．借助这个积分，可以把一个随机过程 (被积函数)对另一个随机过程 (积分变量)进行积分．积分变量一般属于布朗运动范畴．积分结果是一个随机

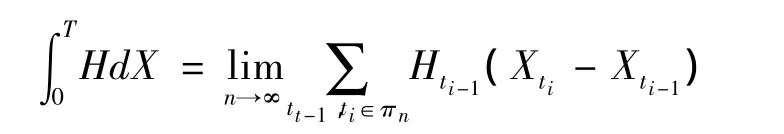
3 Stratonovich积分和it积分

对于伊藤积分和斯特拉托诺维奇积分之间的关系，可以通过以下例题来表述．

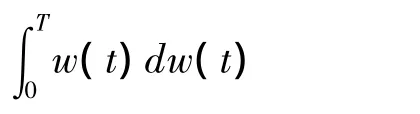
例:求值变量，这个随机变量定义为一特定随机变量序列的极限．

伊藤积分的构造也是根据黎曼和的形式定义出来的，但是由于被积函数是随机过程，所以不同于一般的黎曼积分的构造方式．这里首先要明确，积分对象，也就是什么函数可以为伊藤可积．令V=V(S，T)表示一个函数集合，里面函数满足f(t，ω)∶［0，∞)× Ω － ＞ R 满足:

(1)循序可测性;

(2)关于给定的自然流是适应的;

(3)f在S到T上关于变量t是平方可积的．

对于可以写为离散求和形式的函数，可先直观的写为为伊藤积分的黎曼和形式，剩下的可以分为3个步骤，即:

(1)对于v中有界且固定ω时关于变量t连续的g给出积分定义．找到初等函数列逼近此g，并证明其在L2空间中收敛到g，并证明L2空间中收敛到g．

(2)对于V中有界的函数h给出积分定义．方法是做局部光滑化，回到步骤1中函数．

(3)对于V中一般函数f，找一个有界函数列逼近它．

所以，伊藤积分是对半鞅X以及随机过程H的积分为:

解:

用函数v(t)来近似w(t)，则设

a=t0＜t1＜ … ＜tn，h=(b－a)/n，

且 v(t)= λw(tk)+(1 － λ)w(tk－1)，tk－1≤t≤tk，∀0≤ λ ≤1，

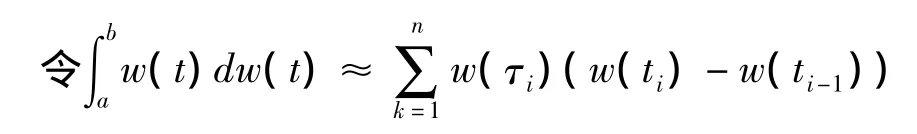
则将上式带入整理得:

渗沥液A/O系统O池为好氧处理工艺，O池的曝气量与除臭风量及加盖密封效果有直接的关系。在方案确定前对曝气量进行了实地监测，依据实际运行的曝气量乘以1.2倍的安全系数，确定除臭系统的风量，以保证加盖后的O池在运行过程中处于微负压状态。

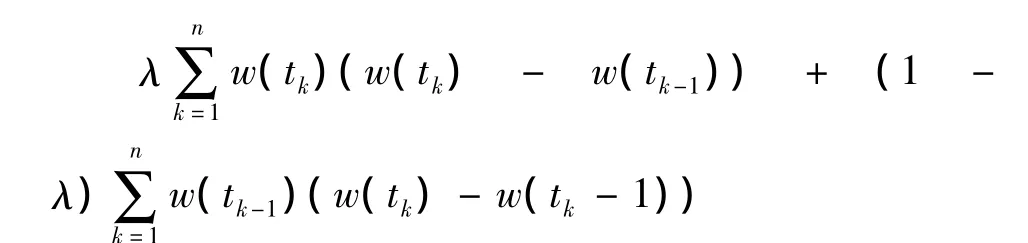
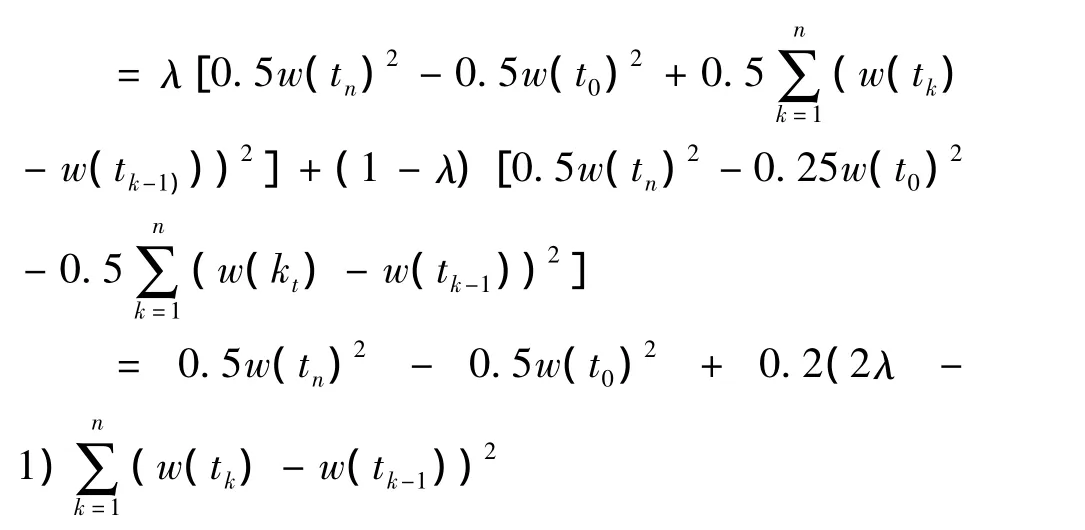
而当上式λ取值不同时，所求的积分值也不同．

当 λ = 0.5 时，τi= 0.5(τi－1+ τi)，

由上面可以看出，可以定义两类积分．其中时，所得积分为伊藤 (It)积分;当λ=0.5时，所得的积分称为斯特拉托诺维奇 (Stratonovich)积分．两者虽有差别，但是在一定条件下可以相互转换．

而通常随机微分方程的积分形式为:

从例题可以看出，伊藤积分和通常积分不同，按照通常积分法则式，右端只有第一项，而伊藤积分的结果还要加上修正项 －(b－a)/2，这是为了保证伊藤积分是一个鞅，也就是:

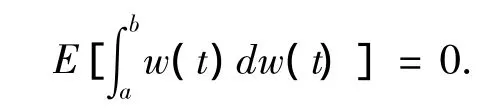
所以，It微分方程和Stratonovich微分方程存在以下关系:

在标量形式下令:

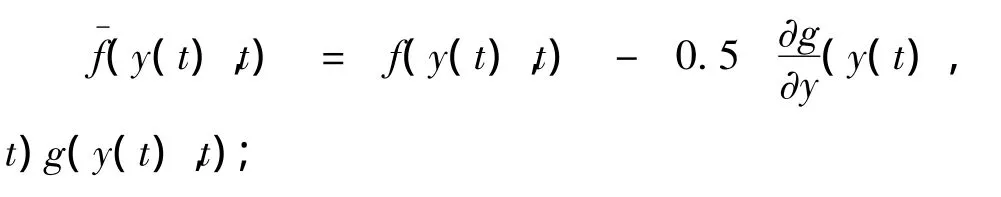
在矢量形势下令:

所以，

又因为当通常随机方程中的第二个积分为Stratonovich积分时，其对应的微分形式为:

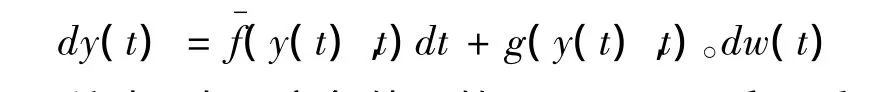
所以，在一定条件下的Stratonovich和it积分可以相互转换．作为拓展，把Stratonovich的多重积分记为:

其中，ji∈{0，1，…，d}对应标号不同的d个维纳过程，并且。dw0(si)≡ dsi．为了方便，可以将Jj1，j2，…jl(t)简单写作 J(j1，j2，…，jl)，其积分形式写作

例如:

j10多重积分记做:其中其中ji∈{0，1，…，d}，对应标号不同d个维纳过程并且dw0(si)≡ dsi。在本文中I(j1，j2，…，jl)(t)可以简单记为I(j1，j2，…，jl)，该积分可写作

由于上述文章中的高阶数值方法使用了两种随机积分，［t，t+h］上的J1和J10/h，它们可以通过两个独立随机数得到u，v～N(0，1)得到

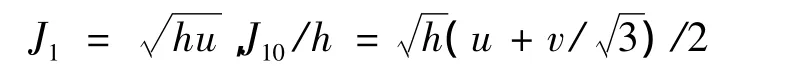
所以，常见的Stratonovich积分和it积分之间的关系有: