车道被占用城市道路通行能力综合分析*

2014-07-09董慧娟陈望云朱家明

九江学院学报(自然科学版) 2014年1期

董慧娟陈望云刘岩朱家明

(1安徽财经大学金融学院;2安徽财经大学统计与应用数学学院安徽蚌埠 233030)

车道被占用是指因交通事故等因素导致车道或道路横断面通行能力在单位时间内降低的现象。由于城市道路具有交通流密度大、连续性强等特点，一条车道被占用，也可能降低路段所有车道的通行能力，即使时间短，也可能引起车辆排队，出现交通阻塞。如处理不当，甚至出现区域性拥堵。本文依据见2013年全国大学生数学建模竞赛A题［1］，分析解决实际通行能力的影响因素以及事故发生后产生的对实际通行能力、车流量、排队长度的影响。

1 实际通行能力的影响因素分析

1.1 建模准备

1.1.1 系数的修正影响道路通行能力的主要因素有车道数、车道宽、侧向净宽、沿线状况、小客车当量系数、红绿灯等。根据事故发生数据，车道数由3个变为1个，车道宽为3.25m，侧向净宽为0.65m。根据道路沿线状况可以判断该道路属于完全城市化区域;从可行性出发，只统计视频中的大客车和电瓶车。根据《道路交通设计规范》，可得到视频中车道宽度的修正系数为0.94，侧向净宽的修正系数为0.98，城市化程度的修正系数为0.75，大客车的换算系数为2，电瓶车的换算系数为0.5。

1.1.2 基本通行能力由于实际通行能力等于基本通行能力和各修正系数的乘积，故先要建立基本通行能力模型。基本通行能力指在理想的道路和交通条件下，当具有标准长度和技术指标的车辆，以前后两车最小车头间隔连续行驶时，单位时间内通过道路上指定断面的最大车辆数，记作CB(辆 /h)。记车速为v(km/h)，前后两车最小车头间隔为d(m)，则有:

最小车头间隔主要由刹车距离决定，而刹车距离又与车速密切相关。常用如下公式计算:

其中d1是刹车时司机在反应时间t0内汽车行驶的距离，d2是刹车时从制动器开始起作用到汽车完全停止行驶的距离，称制动距离，c是与车辆自重、路面阻力、湿度、坡度等诸多因素有关的系数，d3是两车之间的安全距离，d4是车辆的标准长度。

将式(2)代入式(1)，并注意到v(km/h)和d(m)，t0(s)的单位换算，可得:

取理想交通条件下小客车的车速为60km/h，t0=1s，c=0.01，d3=2m，d4=5m，由式(3)计算出CB=10086(辆 /小时)。

1.2 模型的建立与求解

1.2.1 实际通行能力模型用各修正系数乘以基本通行能力，即得在一定环境条件下的实际通行能力，记作CL(辆 /小时)，

其中H表示车道数为单向车行道的车道数，rι表示车道宽度的修正系数，rc表示侧向净宽的修正系数，rz表示沿线状况的修正系数，rT表示大客车的修正系数，rt表示电瓶车的修正系数。

一般认为，大客车的修正系数随着大客车的混入率、换算系数、坡度大小及长度而变化，即:

其中γT表示大客车的修正系数，ET表示大客车的当量小汽车换算系数，T表示大客车的混入率(%)。

同理电瓶车的修正系数的计算公式如式(6)。

其中γt表示电瓶车的修正系数，Et表示电瓶车的当量小汽车换算系数，t表示电瓶车的混入率(%)。

1.2.2 只有车道一可通行时事故横断面处的实际通行能力由于事故发生处上游的四岔路口有一红绿灯，故考虑红绿灯信号周期的影响，以60s为间隔来统计单位时间内大客车与电瓶车的混入率 (见表1)。这样可避免因计时点的不同而导致实际通行能力的计算误差。

表1 大客车和电瓶车从事故发生到撤离的混入率

由表1中的混入率计算出其修正系数，又CB=1006(辆/h)，H=1，rL=0.94，rC=0.98，rz=0.75代入 (4)，得出实际通行能力如表2。

表2 事故横断面的实际通行能力的变化

图1 事故所处断面的实际通行能力变化图

结合表2中的数据利用Excel，可得实际通行能力的变化折线图，结果如图1所示。从图1可知，视频1中事故所处横断面的实际通行能力大致在695辆/公里上下波动。在事故发生后的5min内，实际通行能力不断增加，原因是这段时间内交通量并没有达到最大通行量，在5～12min内，因交通量增加，道路出现拥堵，实际通行能力下降，直至事故撤离后，通行能力才再次回升。

1.2.3 仅有车道三可通行时事故横断面处的实际通行能力根据视频2，得出大客车和电瓶车的混入率，代入 (5)(6)得出大客车和电瓶车的修正系数其他修正系数均不变，代入 (4)计算出仅有车道三可通行时的实际通行能力，如表3所示。

表3 事故横断面的实际通行能力的变化

根据表3中的数据利用Excel作图，结果如图2，可知视频2中事故所处横断面的实际通行能力大致在694.5～695.5辆/公里之间波动。

图2 事故所处断面的实际通行能力变化图

1.2.4 仅车道一和车道三通行时实际通行能力的差异分析为了清晰地比较视频1和视频2事故所处横断面的实际通行能力的差异，利用Matlab编程，把仅车道一和车道三通行时的实际通行能力在同一坐标中展现出来，如图3所示。

图3 两条实际通行能力的曲线比较图

由图3可以看出，视频1事故所处横断面的实际通行能力大体上都比视频2的大。由视频1和视频2的单一车道的密度数据，作出两个车流量的比较图，如图4，又计算出车道一和车道三的平均密度分别为100.91辆/公里、106.39辆/公里，表明视频2车道一，二被占后车辆的阻塞程度大于视频1车道二，三被占后的。

由视频1和视频2的单一车道的车流量数据，作出两个车流量的比较图，如图5，又计算出车道一和车道三的平均车流量分别为1211.25辆/公里、1264.138辆/公里，可以看出视频1中车道一的车流量大部分小于视频2中车道三的，说明事故的占道不同导致车流量不同。这与下游车辆的右转、直行及左转比例不同有关。为了定量分析车辆改道对实际通行能力的影响，引入车道变换系数对其进行修正。

由于车道变换行为涉及多个车道，因此道路通行能力修正系数为:

式中Q为交通量，Qs为损失交通量，nk为车道数，kj为上、下游断面之间的交通阻塞密度，qi为车道变换行为发生率，ιg为单位时间车辆在自由流速Vf下运行的距离，Δv为执行车道变换行车辆的速度与Vf的差值，tc为单位时间损失的交通量。

图4 车道密度比较图

图5 车流量比较图

假设同一条道路上车量需求量不变，所以该道路下游车辆右转、直行及左转比例为每一条车道上的车辆比例，即车道一、二、三上车辆的比例分别为21%、44%、35%。故视频1中 q1=0.79，视频 2中 q2=0.65，又 |Δv|tc1=0.03，| Δv|tc2=0.025，Vf=60km/h，Kj=160pcn/(km/h)，nk=3，代入 (7)得视频1和视频2的车道变换修正系数分别为 rj1=0.83778，rj2=0.868687，由此得出修正后实际通行能力并作图，见图6、7。由图可知在加入车道变换系数后，视频2的实际交通能力反而大于视频1的，因此车辆改道对实际通行能力确有影响。2车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系

图6 视频1修正后的通行能力

图7 视频2修正后的通行能力

2.1 建模准备

由于交通堵塞时引起的车辆排队现象是不定时的，因此以60s为时间间隔来计算当量排队长度。路段上游车流量是与车辆密度有定量关系，因此可以通过车辆密度来计算车流量。然后利用回归分析分别拟合出路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量的关系，建模思路通过流程图如图8所示。

图8 建模思路图

2.2 模型的建立与求解

2.2.1 多车道路段平均当量排队长度模型假设交通流分为阻塞交通流和最佳交通流，阻塞交通流指的是密度达到阻塞密度的交通流，最佳交通流指的是流量达到最大的交通流，当量排队长度即为阻塞交通流的长度。对于单入口单出口的多车道路段，当交通流拥挤时，车辆换道现象是一个事实。因此本文把所有车道看作一个车道组，虽然每一条车道的当量排队长度不一样，但可以计算平均值来描述多车道路段整体上的当量排队长度。

根据流量守恒原理，可知:

其中N0为初始时刻上、下游断面之间的车辆数;NU(t)为t时刻通过上游断面的车辆累计数;ND(t)为t时刻通过下游断面的车辆累计数;ΔN(t)为t时刻上下断面之间的车辆数。

根据二流理论，ΔN(t)可由 (8)计算得到:

其中LD(t)为t时刻上、下游断面之间的当量排队长度;L为上、下游断面之间的距离;km为上、下游断面之间的交通流最佳密度;kj为上、下游断面之间的交通阻塞密度。

联立式 (8)和式 (9)，解得基于二流理论的单车道当量排队长度

由 (11)推导出多车道路段平均当量排队长度模型，即

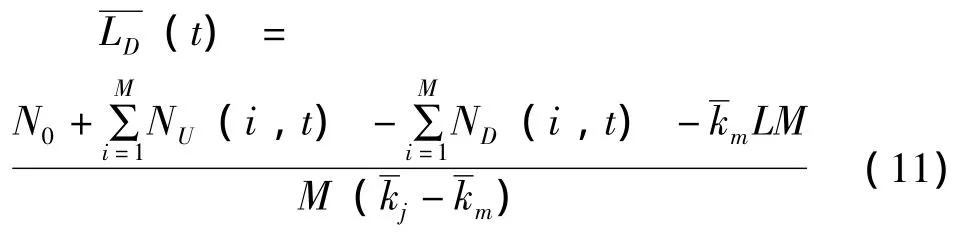
2.2.2 路段上游车流量流量q、速度v和密度k

三者满足关系式:

1935 年，Greenshields［5］通过对观测数据的统计分析，提出车速与密度之间的一个线性模型，即:

将式 (13)代入式 (12)，得到流量与密度的关系［6］:

2.2.3 多车道排队长度模型的求解以一个信号周期 (60s)为时间间隔记录时刻上游断面的车辆累计数NU(i，t)和下游断面的车辆累计数ND(i，t)，并把大客车和电瓶车换算成标准小汽车的累计数。

由格林伯速度－密度模型:

又N0=20.5辆，L=0.24km，M=3，代入式(11)得出多车道的当量排队长度，如表4所示。

表4 多车道的当量排队长度

2.2.4 事故持续时间的记录事故持续时间可以从视频中直接读取，选取和当量排队长度对应的11个信号周期，结果如表5。

表5 当量排队长度对应的11个信号周期

2.2.5 路段上游车流量的计算取kj=160辆/公里，vf=60km/h，统计当量排队长度对应的11个信号周期的密度，把k、kj、vf代入式 (14)，得出上游车流量q，结果如表6所示。

表6 上游车流量值

2.2.6 回归分析把当量排队长度作为，实际通行能力作为，事故持续时间作为，上游车流量作为，用Excel拟合分析，拟合结果如图9、10、11所示。

图9 y与x1的拟合图

图10 y与x2的拟合图

图11 y与x3的拟合图

由图9、图10、图11可以看出 y与 x1、x2、x3的关系都近似为一个二次函数，曲线方程分别为y= －0.0203x21+28.177x1－9753.9，y= －11.3x22+4.7732x2－0.2726，y= －8×10－8x23+0.0001x3－0.1935。3个方程的拟合优度分别为0.6244、0.9113、0.7255，因此3个拟合方程均成立。

用多元线性回归模型拟合y与x1、x2、x3的线性关系。运用Matlab编程，结果见表7和图12，可得多元线性回归模型为:y=14.2381－0.0202x1+0.5982x2－0.0001x3。