车道被交通事故占用城市道路通行能力探究*

韩 军 武伟静 桂雪晴

(安徽财经大学商学院 安徽蚌埠 233030)

车道被占用是指因交通事故、路边停车、占道施工等因素，导致车道或道路横断面通行能力在单位时间内降低的现象。由于城市道路具有交通流密度大、连续性强等特点，一条车道被占用，也可能降低路段所有车道的通行能力，即使时间短，也可能出现交通阻塞。如处理不当，甚至出现区域性拥堵。研究车道被占用对城市道路通行能力的影响及车辆排队问题是一个很有价值的课题。本文基于2013年全国大学生数学建模竞赛A题［1］。所给数据和相关文献，对车道被占用时道路横断面实际通行能力的变化，排队长度与事故横断面道路的实际通行能力、事故持续时间和路段上游车流量之间的关系等问题进行研究

1 研究道路实际通行能力的变化过程

1.1 数据处理

根据视频中的数据首先截取事故发生以前事故发生时以及事故发生以后按照时间序列中计算每一分钟出车流量数目，然后在根据视频中提供的120m的横断面长度标准当量车车头通过横断面的起点到车头到达横断面终点从而计算出车辆的速度。又因为当上游路口绿灯亮时，最前面的车辆车速相对后面比较快，因此笔者把一段车流可分为前、中、后求出他们各自的速度再把他们平均化求出每辆车的平均速度，进而计算横断面的实际通行能力。车辆换算表 (车辆折算标准来自《公路工程技术标准［2］(JTG B01—2003)》)，详见表1。

表1 交通量调查车型划分及车辆折算系数

1.2 模型的建立与求解

1.2.1 模型Ⅰ:交通流模型 流量、速度、密度之间的关系式叫做交通流模型［3］。根据调查观测得到的交通资料假设车流均匀、车种单一时，得到车流速度、密度、流量之间的理论关系式，这就是交通流基本模型，可用下式表示:Q=VsK式中:K为交通密度(辆 /km);Q是交通量(辆 /小时);VS是空间平均车速(km/小时)。20世纪30年代初，格林希尔兹(Greenshield)在研究美国公路车流中，提出了速度与密度的线形关系，这一模型简单直观，研究表明，这一模型与实测数据拟合良好。可用公式表示:V=aK+b。式中a，b是待定系数，当密度趋于零时，空间平均车速接近于自由行驶车速，即K=0时，Vs=Vf(为自由行驶车速)。将此关系代入式中得b=Vf。当密度很大，车辆无法行驶时，这时的密度称为阻塞密度，以Kj表示，即K=Kj，Vs=0，代入式中得a= － Vf/Kj。将a、b系数代入式得速度—密度关系式:

流量与密度的关系:将速度—密度关系式代入速度、密度、流量的理论关系式，得到流量—密度关系式:

流量与密度是两次抛物线的关系，如将流量q对密度K微分，并令其等于零，即可得到流量Q极大值及对应的密度，此时的密度为最佳密度，以Km表示，即可得:

将代入，得到流量与速度关系式:

当交通密度很大时，可以采用格林柏(Grenberg)提出的对数模型:

式中:V表示最佳速度。

利用流量与密度、流量与速度的关系，计算事故发生前后车辆通行能力，结果如表2所示。

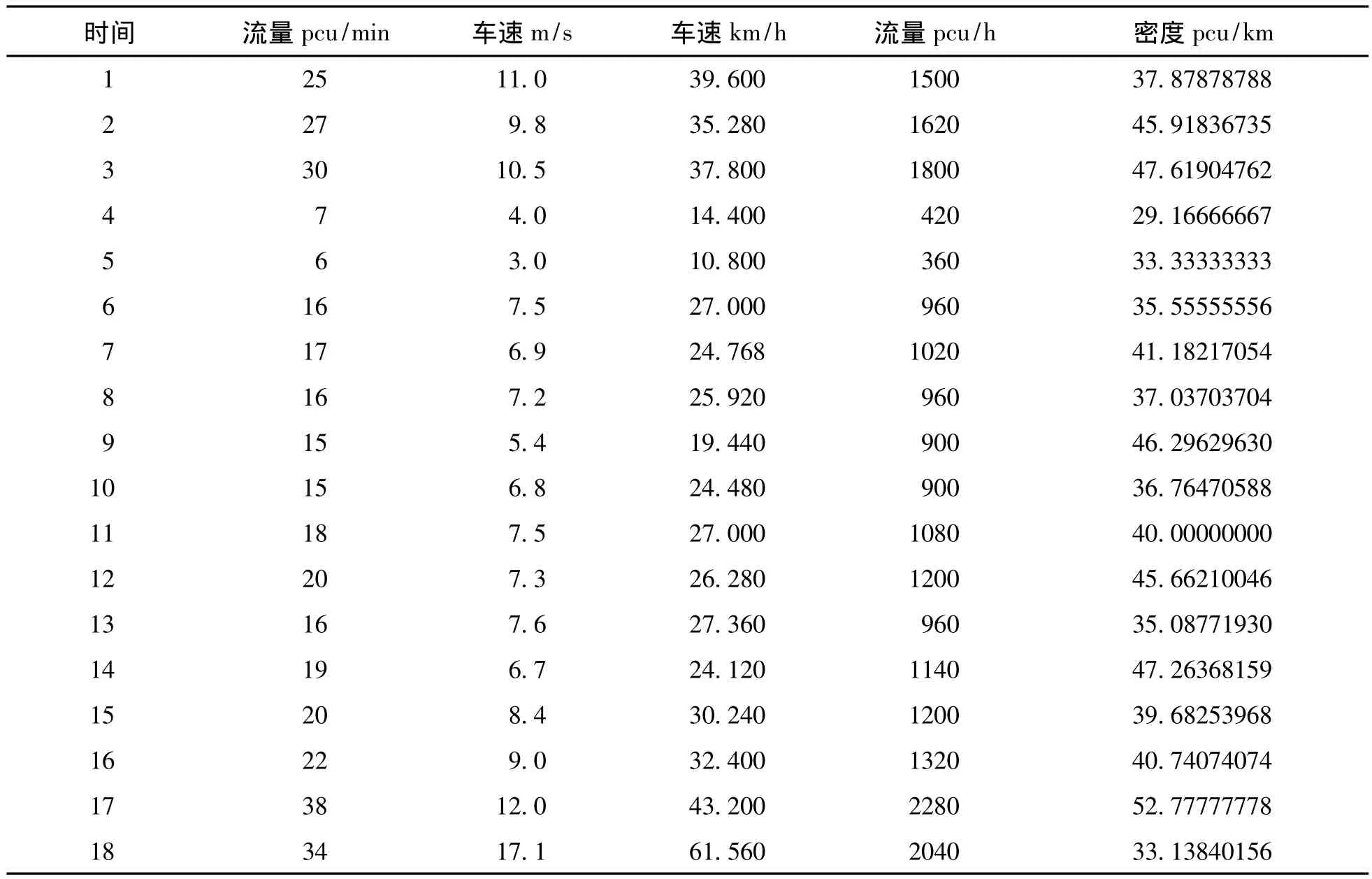
表2 事故发生前后统计交通流量变化

可知在事故发生之前横断面实际通行能力为29～37pcu/min，事故在二、三车道发生以后二、三车道被迫停止通行，增大车辆前行阻力。此时横断面实际通行能力为14～17pcu/min．。图1中事故发生以前每辆车通过路口的速度大约是35.6～40km/h事故发生以后车辆所处横截面密度不断减小上游路口车辆不断往下游路口行驶导致车辆速度下降为19.5～24.4km/h。

2 同一横断面交通事故所占车道不同对该横断面实际通行能力影响的差异

2.1 建模思路

首先根据同样方法做出与问题一的数据处理，假设交通事发生时不同车道能力是相同的，然后根据秩和检验法。从而确定同一横断面交通事故所占车道不同对横断面实际通行能力影响的差异。

2.2 模型I——非参数秩和检验模型

不同占道事故对道路实际通行能力影响的差异分析，笔者对两种事故的流量、密度以及车速均采用非参数秩和检验［4］，检验结果如表3。

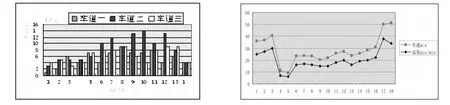
图1 视频一各车道事故发生前后横断面车辆数目与车流量对比图

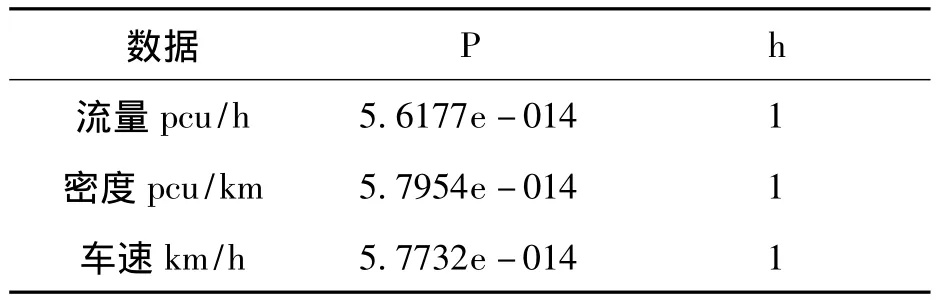
表3 秩和检验结果

由于视频一和视频二中的流量，密度，车速两组数据之间的MATLAB检验概率分别为5.6177e－014，5.7954e－014，5.7732e－014;所以横断面交通事故所占车道不同对该横断面实际通行能力的影响存在高度显著差异。

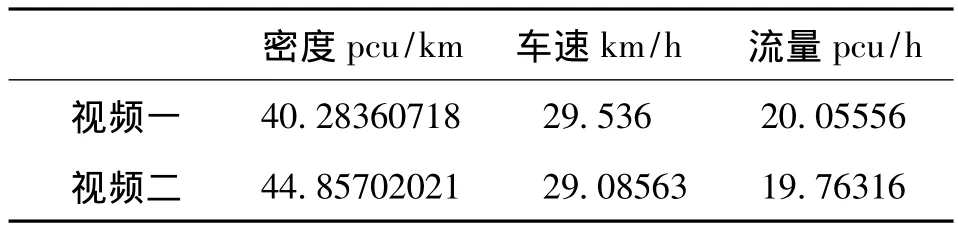
表4 视频一二横断面通行能力

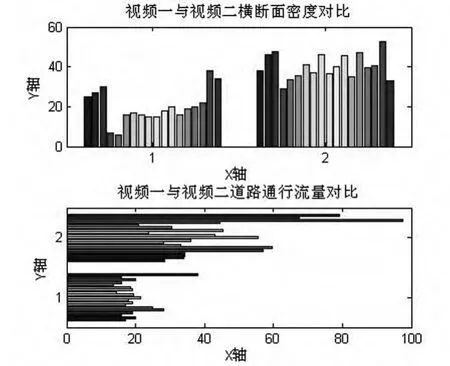
图2 视频一与视频二横断面密度对比

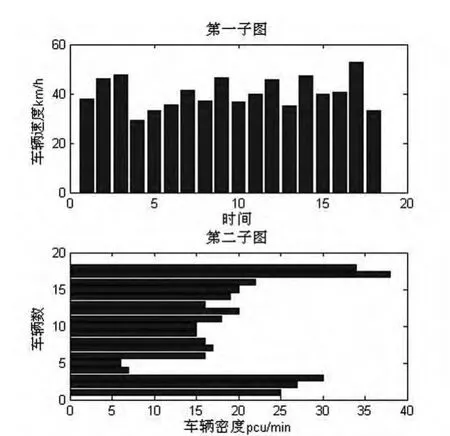
图3 视频二事故发生前后车速与车量对比

上图2、图3、视频一与视频二与道路实际通行流量和二者横断面密度对比可知，视频一中事故所处的横截面车辆滞留数目低于视频二中车辆滞留数目，并且通过统计视频一中车辆通过下游路口数目与视频二中车辆通过下游路口通行流量数目可知视频二中车辆较多。

2.3 模型Ⅱ——综合评价模型

2.3.1 建立理想方案

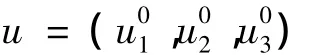
其中:

因为两者视频同一方向车速大致相等，因此计算出视频一和视频二均一化的密度、车速和车流量之间数值如表4所示。

由于第一项指标为成本型，后两项指标为效益型型，故理想方案为:

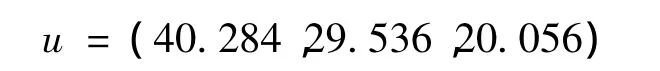
2.3.2 建立相对偏差模糊矩阵 根据公式

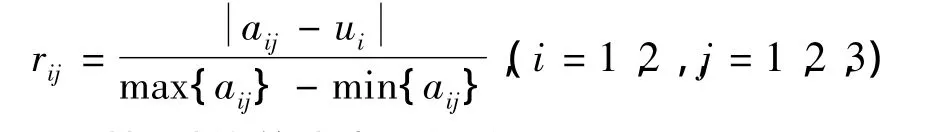
得到相对偏差成本型矩阵:

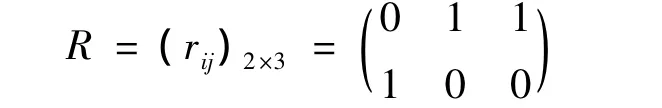
建立综合评价模型［5］。

2.3.3 变异系数法建立权向量

(1)计算各指标的变异系数:

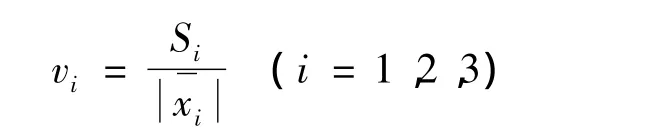
得到:v=(0.0760，0.0109，0.0104)(2)对vi进行归一化求各指标的权数

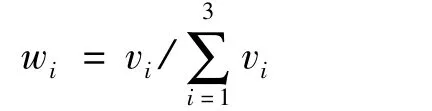
即得权向量:w=(0.7814，0.1118，0.1068)。

2.3.4 建立加权平均综合评价模型:

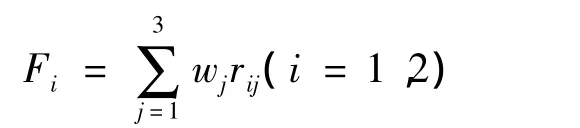
判别准则如下:且若Ft＜Fs，则第t个方案排在第s个方案前。计算得到:F=0.2186，F2=0.7814由此可知:F2＞F1，即第一个方案最优。所以同一横截面的交通事故所占车道实际通行能力车道一车道二对实际交通影响更大。

3 交通事故所影响的路段车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系

3.1 建模准备

交通事故的发生使得实际通行能力出现了变化，当事故路段的车流量大于道路通行量时，造成车辆排队。为了分析事故路段的车辆排队长度与事故横断面实际通行能力、事故持续时间、路段上游车流量间的关系，根据车辆阻塞—消散过程波形时距图和交通波的轨迹方程［5］，进一步推导出事故路段排队长度方程，建立路段排队长度微分方程模型，分析排队长度与各变量指标之间的关系。

3.2 模型的建立与求解

3.2.1 模型 I—— 车辆排队长度微分方程模型［5］在交通事故发生后，本车道上游的流量为q1，对应的密度为k1，事故段的通行能力下降为s1，车流密度相应地上升为kx1。事故排除后，排队车辆以饱和流率驶出，密度为k2。t=0为事故发生时间，y=0表示事故发生点，车流阻塞—消散过程产生的交通波包括线段AB和曲线段BCD，如图4所示。ta是事故排除时间，ta==0.32h。

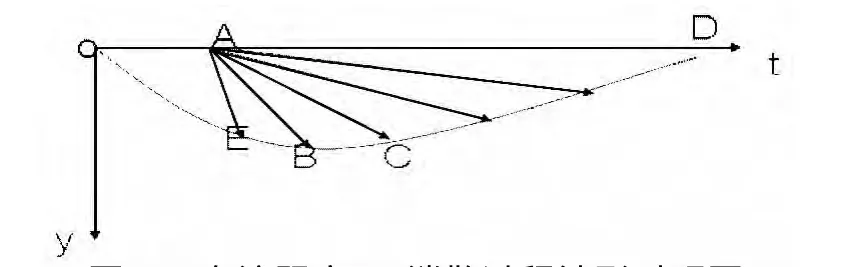
图4 车流阻塞—消散过程波形时距图

OB为事故发生后，交通波的轨迹，波速为:

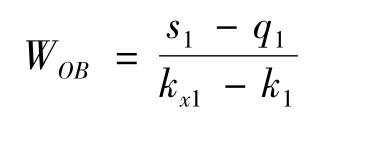
进一步确定为流量密度的关系模型，规定上游车流量q1属于高速低密的畅流态，而s1属于低速高密的拥挤态，kj表示阻塞时的车速，称阻塞密度，取kj=10pcu/km.。vf是密度为零时的车速，即理论上的最高车速，称畅行车速(自由流)，取 vf=120km/h。则有WOB=vf(1－kx1+k1)/kj解三角形可得出:

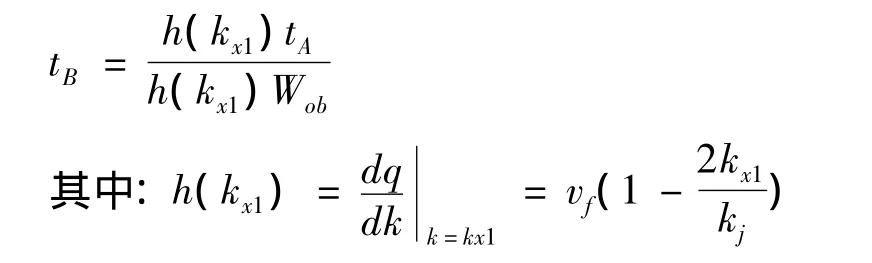
设kR表示曲线段BCD上任意一点的交通流密度，则考虑该点的波速为:

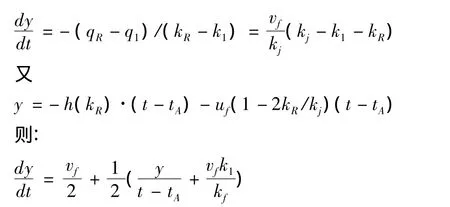
令T=t－tA则方程可化为齐次微分方程h(k1))设y=wT，解微分方程得到该方程的特解，即为曲线段BCD上任意一点的排队长度方程:

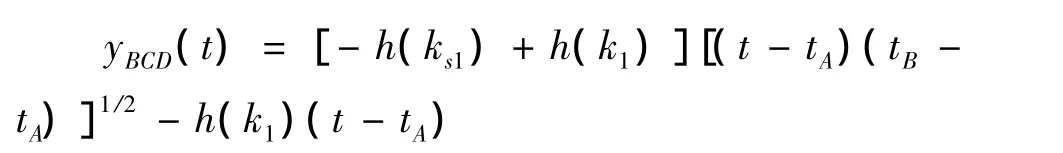
3.2.2 模型Ⅱ——路段上游车流量微分方程模型

对于交通事故所处横断面距离上游路口变为140m，路段上游车流量为1500pcu/h，事故发生点车辆初始排队长度为零，路段下游方向需求不变，且事故持续不撤离。

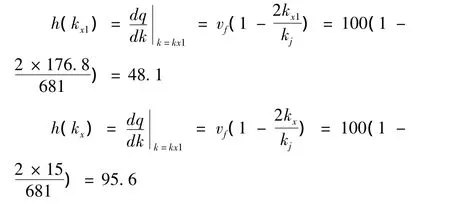
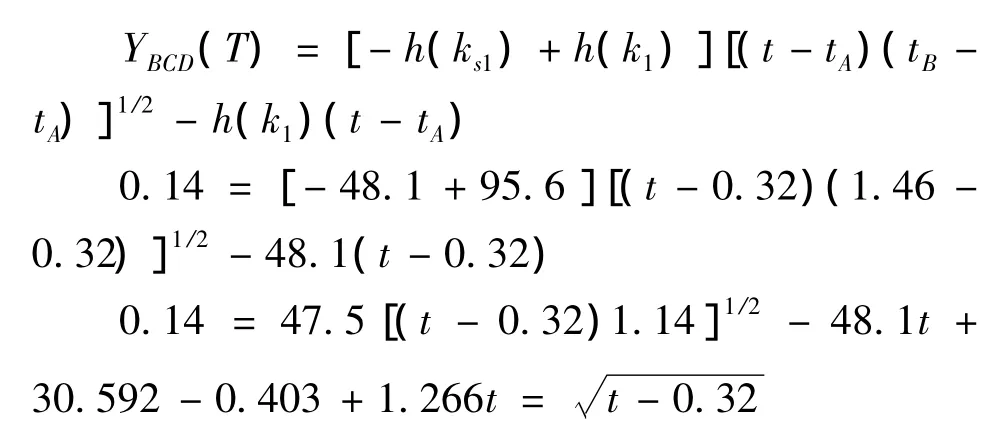
求解无理方程得到t=0.32h和t=0.94h。考虑到实际情况，上游车流量源源不断向事故路段行驶，由于横断面距离上游路口为140米，故舍弃t=0.94h。则最终结果为:t=0.32h，即t=19min

4 结语

基于城市车道被占用对通行能力的影响所使用的交通流模型同时也可以推广到其他方面。例如地震，山体滑坡发生以后根据微分方程模型及时通知过往司机如何最快的安全撤离绕道或给其提供指导性意见以减缓道路拥挤程度，保证城市交通畅通。除此之外，文章中使用的微分方程模型还可以推广到求解溶液浓度的变化规律、人口预测以及传染病这类问题当中。

［1］2013年高教社杯全国大学生数学建模竞赛A题 ［EB/OL］．http://www.mcm.edu.cn/．

［2］中华人民共和国行业标准JTG B01 2003公路工程技术标准 ［S］．2004．

［3］姜启源，谢金星．数学模型 (第4版)［M］．北京:高等教育出版社，2011．38．

［4］李柏年．经济数据处理与优化模型实验教程 ［M］．天津:天津大学出版社，2009．143．

［5］臧华，彭国雄．城市快速道路异常事件下路段行程时间的研究交通运输 ［J］．系统工程与信息，2003，3(2):57．

［6］李柏年，吴礼斌．MATLAB数据分析方法 ［M］．北京:机械工业出版社，2012．49．

［7］杨桂元，黄己立．数学建模 ［M］．合肥:中国科学技术大学出版社，2009．156．

［8］陈仲生，基于Matlab7.0的统计信息处理 ［M］．长沙:湖南科学技术出版社，2005．141．