一个修正的数值积分及在凸轮设计中的应用①

王小炼， 金玲玲， 赵 锋， 王勇勇， 章雷宇

(台州学院数学系，浙江临海317000)

在凸轮构中，由加速度进行积分求得位移是设计凸轮运动特性的一个重要方法之一[1，2]．当前实际生产中是使用正弦函数或变形正弦的加速度，通用加速度曲线[3]．它由于计算简单，因此被广泛使用．但这种加速在边界上是不光滑的，因此在高速运动时，会产生明显的振动．为了解决这个问题，许多学者采用样条函数来设计角加速度[4～7]，但由于其函数表达式比较复杂，很难给出其角位移函数的初等表达式，因而常常采用数值积分的方法来计算角位移．但这种计算需要两次数值积分，因此它会产生较大的累计误差．为了解决这个问题，在此引入一种修正的梯形公式来优化样条函数的数值积分．

1 主要结果

1．1 常用数值积分公式

1．1．1 复合梯形法

设函数 f(x)在[a，b]上连续，对[a，b]n等分，则复合梯形公式为:

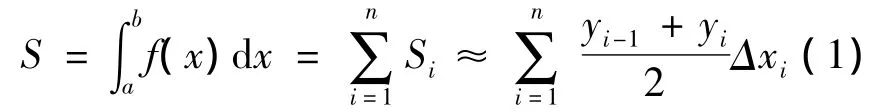
其中 yi=f(xi)，i=1，2，…，n，xi为等分点．

1．1．2 辛普森法

辛普森法(Simpson＇s rule)是一种数值积分方法，是以二次曲线逼近的方式取代矩形或梯形积分公式，以求得定积分的数值近似解．

将积分区间[a，b]作2n等分，设h=(b－a)/(2n)．

1．1．3 四阶 Adams法

假设已经求得tn，tn－1，…，tn－k等k+1 个节点处的函数值 fn，fn－1，…，fn－k，根据插值原理可以构造一个多项式来逼近函数f(t，y)，经过计算处理可以得到

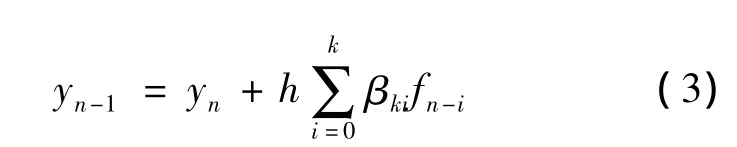
4阶阿达姆斯显式公式

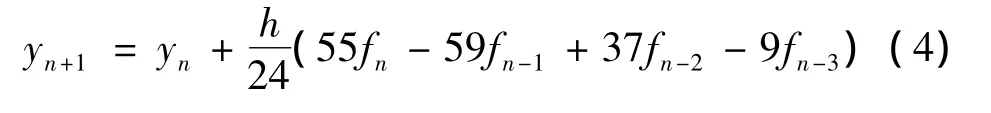
1．2 改进梯形法

文献[8]给出了下列Euler公式

定理1 设函数f(x)在[a，b]上具有(n－1)阶的连续导数，自然数m≤n/2，记

如果 n=2r－ 1，r≥1，那么

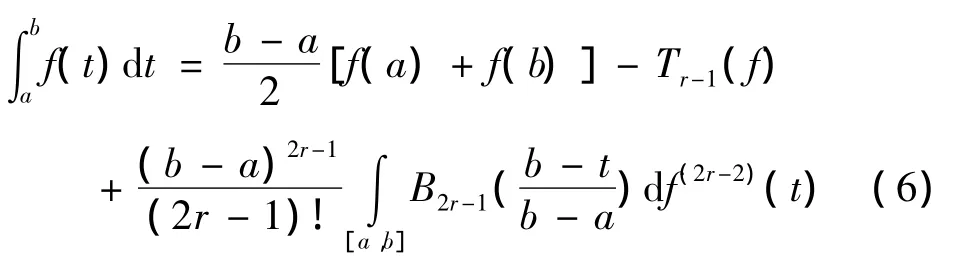
当r=2时，那么对积分取近似值得

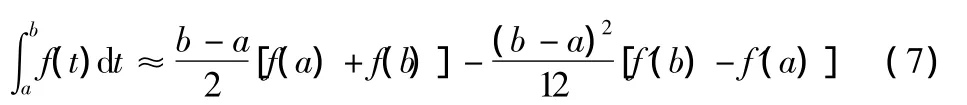
当r=3时，那么对积分取近似值得

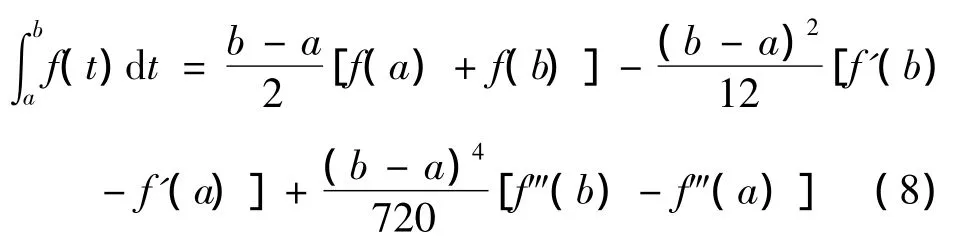
将(7)式两边关于b积分，得到

经过化简可以得到，

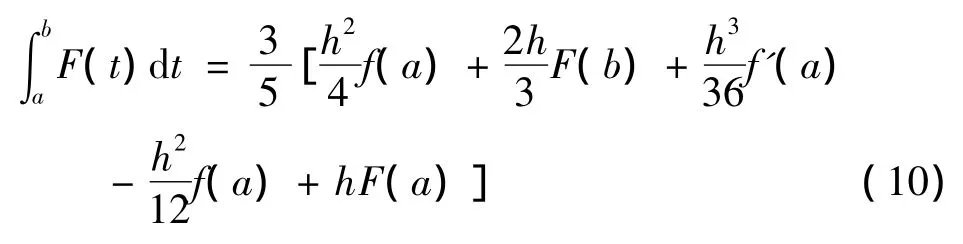
再将(7)式两边关于a积分，化简得到

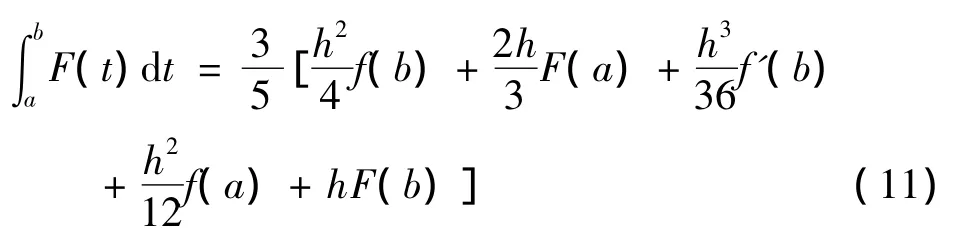
其中，F(t)是f(t)初值为零的原函数．

将(10)与(11)相加除以2得到了式(12)

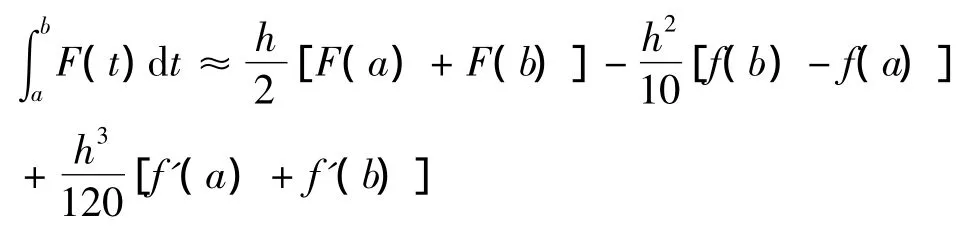
定理2 (1)设函数f(x)在[a，b]上具有连续导数，则f(x)的两次数值积分可用下式近似

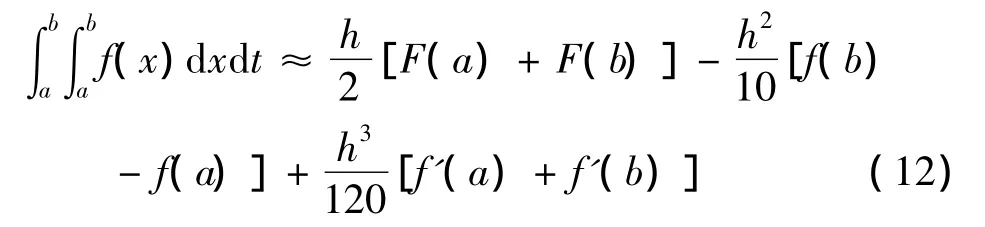
(2)设函数f(x)在[a，b]上具有(n－1)阶的连续导数，自然数m≤n/2，则

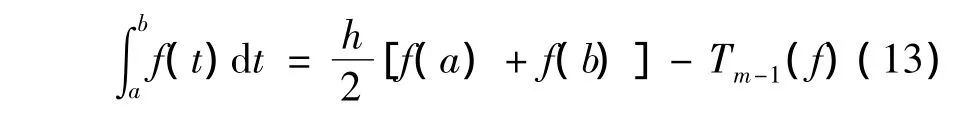
其中h=b－a．

在式(13)只要选取适当的m，就可得到了一种可以将精度提高到六阶甚至更高阶的方法．

注:在凸轮曲线的设计中，改进梯形法式(12)只需一次就可以得到位移曲线，比(7)需两次进行数值积分，其计算量少了一次．

2 数值例子

结合以下实例:

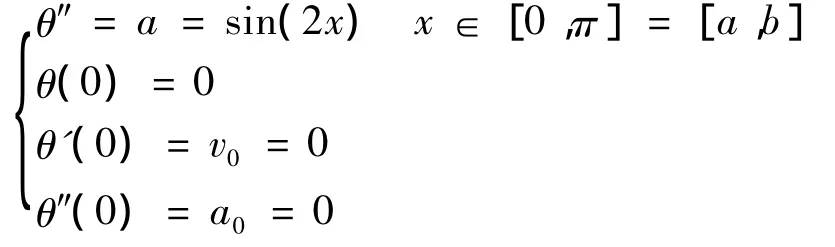
利用上述函数对各种数值积分法进行对比检验．其中辛普森法、四阶Adams法的精度只有四阶．对此在式(13)只要选取适当的m，就可得到了一种可以将精度提高到六阶甚至更高阶的方法．

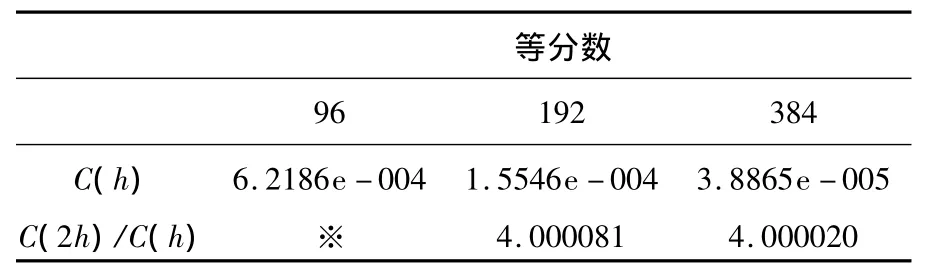
表1 复合梯形法的数值解θ的逐点误差最大值与阶数

由表1可以得到，梯形法的误差的阶数为二阶．

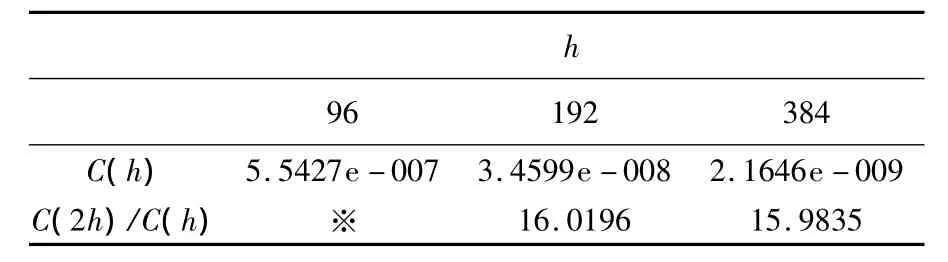
表2 辛普森法的数值解θ的逐点误差最大值与阶数

由表2可以得到，辛普森法的误差的阶数为四阶．

表3 Adams 法的数值解θ的逐点误差最大值与阶数

由表3可以得到，Adams法的误差的阶数为四阶．

表4 改进梯形法式(13)选取(m=2)θ的误差最大值与阶数

由表4可以得到，改进梯形法(m=2)的误差的阶数为四阶．

表5 改进梯形法式(13)选取(m=3)θ的误差最大值与阶数

由表5可以得到，改进梯形法(m=3)的误差的阶数为六阶．

表6 6种方法的数值解的θ的逐点误差最大值比较

改进梯形式(12)4．0037e－008 2．5021e－009 1．5638e－010

对以上表格进行分析，在分割间隙相同时，改进梯形法的误差优于辛普森法的误差再优于Adams法的误差，最差的是复合梯形法．由此可知，改进梯形法的误差最小．

表7 两种改进梯形法式(7)与式(12)的对比

在凸轮曲线的设计中，改进梯形法式(12)只需一次就可以得到位移曲线，比(7)需两次进行数值积分，其计算量少了一次．且其精度也比(7)较优约提高10%左右．

谢辞:本文的写作得到了台州学院数学系赵岳清副教授的精心指导，在此表示感谢．

[1] Chen F Y．Kinematic Synthesis of Camprofiles for Prescribed Acceleration by a Finite Integration Method[J]．Engineering for Industry，1973(2):519 －524．

[2] 齐维浩，李雨宏．按复杂边界条件设计凸轮曲线[J]．机械工程学报，1985，(3):60－66．

[3] 刘昌祺．凸轮机构设计[M]．北京:机械工业出版社，2005，10．

[4] 韦日钰，滕弘飞，隋允康．五次样条配气凸轮型线动力优化设计[J]．内燃机学报，1993(4):360－367．

[5] 韦日钰．具有给定加速度特性的五次样条凸轮曲线设计[J]．广西大学学报，1998，(9):249－254．

[6] 徐健，常学芳，薄玉成．三次样条在转管武器凸轮曲线中的应用[J]．机械工程师，2007(7):83－84．

[7] 张洪．探讨一种凸轮理论曲线的通用方程式[J]．机械传动，2007(4):99－101．

[8] Lj．Dedic，M．Matic，J．Pecaric．On Euler Trapezoid Formulae[J]．Appl．Math．And Compu．123(2001):37 －62．