对几种SPH 方法的对比研究①

热合买提江·依明， 买买提明·艾尼

(1．新疆大学数学与系统科学学院，新疆乌鲁木齐830046．2．新疆大学机械工程学院，新疆乌鲁木齐830047)

0 引言

光滑粒子流体动力学(Smoothed Particle Hydrodynamics，简称SPH)方法是一种新的无网格纯Lagrange粒子方法．1977年，由 Lucy和 Monaghan[1]等人提出，最初用于解决天体物理学和宇宙学中模拟三维无界空间天体的演化问题．Monaghan等人相继提出了适用于SPH方法的人为粘性和人为热流项后[2]，又延伸到了计算流体力学的各个领域．Libersky和 Petschek[3]在 SPH 中引入了材料强度模型，模拟了动态断裂和破片运动等固体的动态响应，此后SPH被迅速的应用到固体力学的研究当中．由于SPH方法计算过程不需要划分网格、容易编程实现、能够有效处理多种材料界面等特点，发展到今天，SPH方法已广泛地应用于科学工程计算和模拟的各个领域．

SPH方法在许多问题上的应用极大地促进了传统SPH方法的发展和改进．经典的SPH方法在模拟计算中，存在很多问题．例如，精度比较低，在边界缺乏插值一致性，不稳定性等等，于是，便出现了SPH的各种修正方法，以弥补传统SPH方法的一些缺点，这些修正导致了SPH方法表达公式的多样性．

J．K．Chen 等[4]，将函数的 Taylor级数展开用在函数及其空间导数近似上，提出了修正(Corrective)后的光滑粒子流体动力学方法(简称CSPH)．R．C．Batra 等[5，6]，通过将核函数及其空间导数乘到函数的Taylor级数展开式两边后组成方程组的思路，得到改进(Modified)后的光滑粒子流体动力学方法(简称 MSPH)．G．M．Zhang等[7]，通过将核函数及其幂函数序列乘到函数的Taylor级数展开式两边后组成方程组的思路，提出了对称(Symmetric)的光滑粒子流体动力学方法(简称SSPH)．本文给出了每种SPH方法的推导过程和表达式，用一维和二维数值实例对这几种方法进行了详细的对比和误差分析．

1 传统SPH方法的理论基础

1．1 核近似

在SPH方法中，将任意函数f(X)在空间某一点X处的值和各阶(一阶和二阶)导数值用核函数与f(X)乘积的积分来表示，然后用粒子近似方法将积分转化成离散形式的粒子求和式．

设函数f(X)，定义在区域Ω的任一连续函数，如果X∈Ω，则在Ω中将函数f(X)可以表示成如下积分形式

式(1)中，X为位置矢量，δ(X－X')为狄拉克δ(Dirac)函数．

如果可以找到一个近似于狄拉克函数的核函数W(X － X'，h)，用W(X － X'，h)来代替(1)中的 δ(X－X')函数，则函数f(X)的积分表达式可写成．

上式简称函数的核近似，式(2)中W(X－X'，h)称为核函数，它依赖于两点之间的距离|X－X'|和定义核函数影响区域的光滑长度h．由于核函数W(X －X'，h)不是δ(X －X')函数，因此，式(2)只能是近似式．在光滑粒子法中，用 ＜ ＞来表示函数的核近似式，于是，式(2)可以改写为

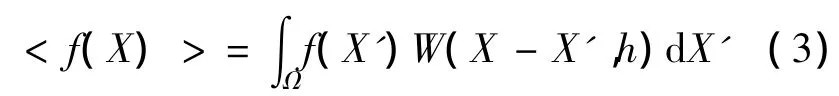
核函数一般若干个性质[8]:

在式(3)中的函数f(X)用函数的空间导数▽f(X)替换，并用分部积分法、高斯定理和核函数性质，可得到函数梯度▽f(X)的核近似式(4)．

同理可得函数的二阶梯度▽2f(X)的核近似式(5)．

可证函数核近似式(3)，(4)和(5)对于光滑长度具有二阶精度[8]．

1．2 粒子近似法

在SPH方法中把整个求解域离散成一系列任意分布有质量和容量的有限多个粒子，如果核近似式中粒子j处微元体dX'的体积为△Vj、质量为mj、密度为ρj、位置矢量为Xj，记函数f(X)在粒子j处的值为，fj=f(Xj)粒子i为中心的核函数影响范围内的粒子总数为N，则函数f(X)在粒子i处的函数及其一阶、二阶导数核近似式(3)、(4)、(5)的核近似粒子求和式分别为．

其中

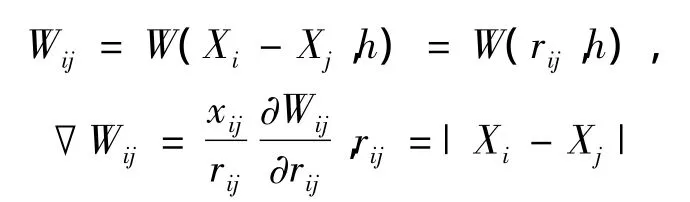
2 其它格式的SPH方法

2．1 CSPH 方法

为了表示简便，假设函数f(X)在直角坐标系中以 x1，x2和x3为自变量的函数，即X=(x1，x2，x3)，则函数f(X)在X'处展开泰勒级数得．

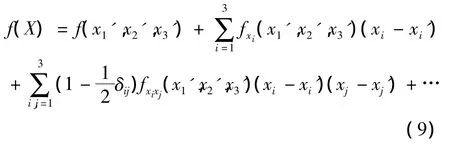
其中，当 i=j时 δij=1，当 i≠ j时 δij=0．

式(9)的两边乘核函数W(X－X'，h)并在核函数影响区域Ω内取积分得

因为∫Ω(xi－xi')W(X －X'，h)dX=0并忽略二级及二阶以上的导数项可得函数的CSPH核近似式为

式(9)的两边乘核函数偏导数▽xjW(X－X'，h)(j=1，2，3)并取积分，忽略二阶及二阶以上的偏导数项后整理可得

当函数为一维时，整理式(12)直接可得函数一阶导数的CSPH核近似式，当函数二维和三维时式(12)分别变成二元和三元方程组．

式(9)的两边乘核函数二阶偏导数▽xixjW(X－ X'，h)(i，j=1，2，3)在Ω上取积分并忽略二阶以上的偏导数项整理得

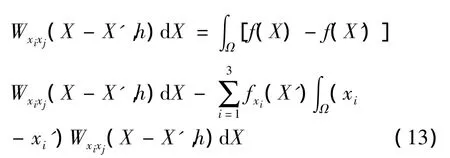
当函数为一维时，由(13)式直接可得函数的二阶导数CSPH核近似式，当函数二维和三维时式(13)分别变成三元和六元方程组．

2．2 MSPH 方法

假设函数f(X)在直角坐标系中以x1，x2和x3为自变量的函数，

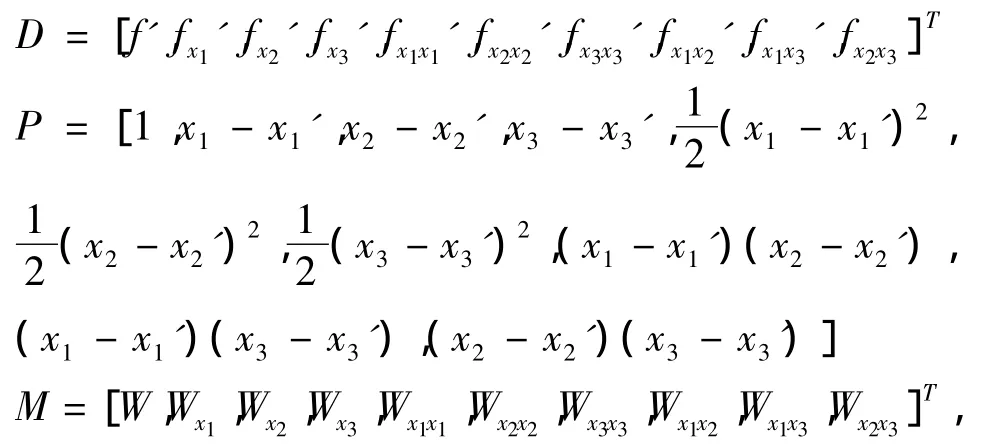
其中

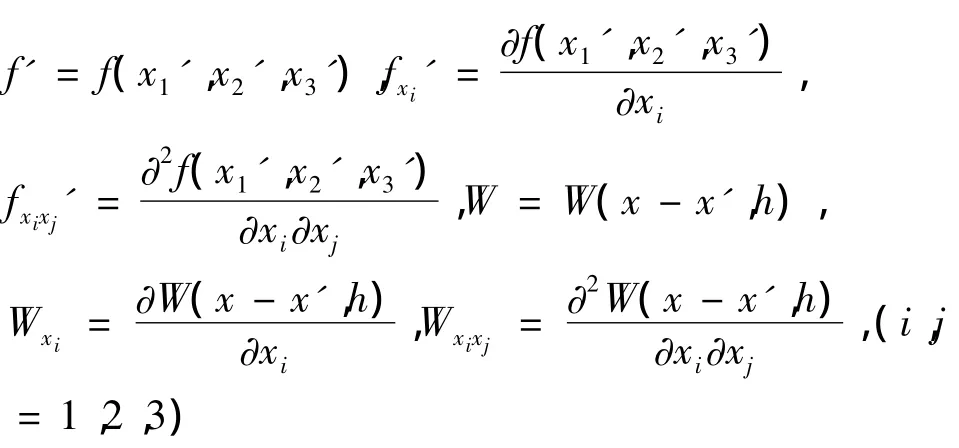
忽略二阶以上的项函数f(X)在X'处的泰勒级数展开式

式(14)的两边分别乘M并在Ω上取积分得

当函数为一维、函数二维和三维函数时，式(15)分别变为三元、六元和十元方程组．

2．3 SSPH 方法

假设S=WPT，式(13)的两边乘S并在Ω上取积分得

当函数为一维、函数二维和三维函数时，式(17)分别变为三元、六元和十元方程组．

3 数值算例

本文中所有数值算例中选用三次B－样条函数，光滑长度为粒子间距的1．2倍．

3．1 一维算例

考虑函数 f(x)=(x － 0．5)4，x∈[0，1]．

区间[0，1]上均匀分布21个粒子时，图1a～1c给出正确值与用SPH，CSPH，MSPH，SSPH方法计算得的函数及其一阶、二阶导数的核近似值对比图．从图1可以看出，在内部区域每一种方法的计算精度没有太大的区别，在边界处SPH方法和CPSPH方法的精度不如MSPH方法和SSPH方法，特别计算二阶导数时，SPH方法和CPSPH方法在边界处的误差变的更大，而SSPH方法的误差最小．

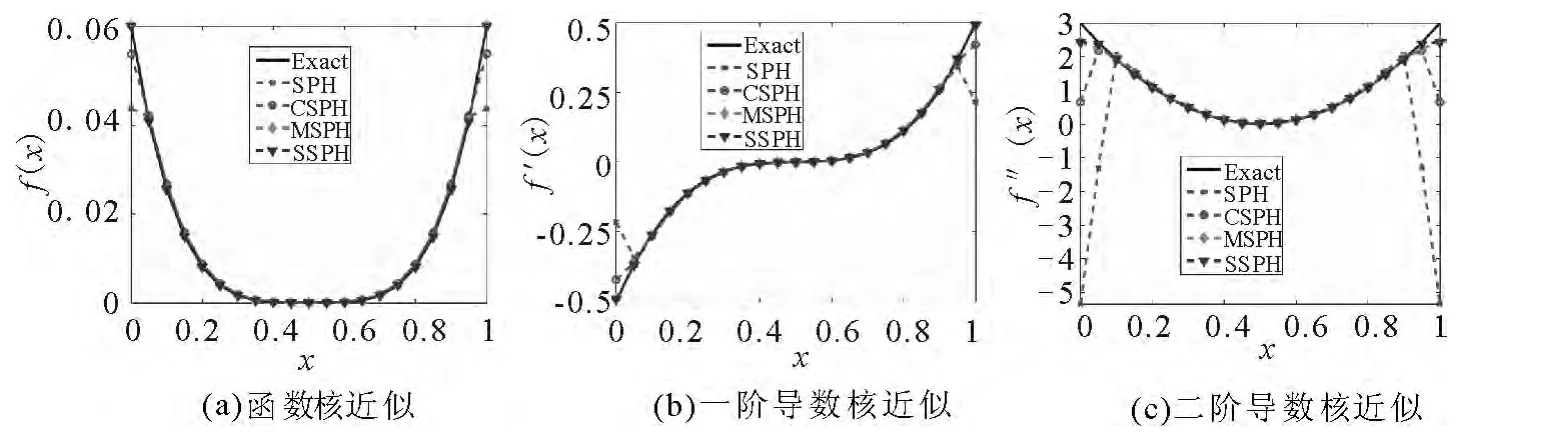
图1 函数核近似

对几种不同类型SPH方法的精度进行更好对别分析，本文引入误差范数比较，误差范数可选择类型有多种多样，本文中误差范数的定义为

其中N是整个计算区域内的粒子数，fExact(xi)分别表示函数及其一阶、二阶导数在i粒子处的值，fCompute(xi)分别表示响应函数在i粒子处的核近似值．

图2给出函数f(x)=(x－0．5)4，x∈[0，1]的区间上均匀分布11，21，41，81，161个粒子时，误差范数比较，结果表明，4种方法的误差都随粒子数的增加而减少，其中SPH方法的误差最大，SSPH方法的误差最小，误差由大到小依次排列为SPH，CSPH，MSPH，SSPH．计算一阶和二阶导数时，随粒子数的增大SPH方法误差的减小不太明显，而MSPH和SSPH方法的误差非常接近．对其它类型的函数如 f(x)=sin(πx)，x ∈ [0，1];f(x)=e－x2，x ∈[－ 1，1]进行计算发现，计算区间上粒子的分布和光滑长度如何改变，SSPH方法的误差还是最小．

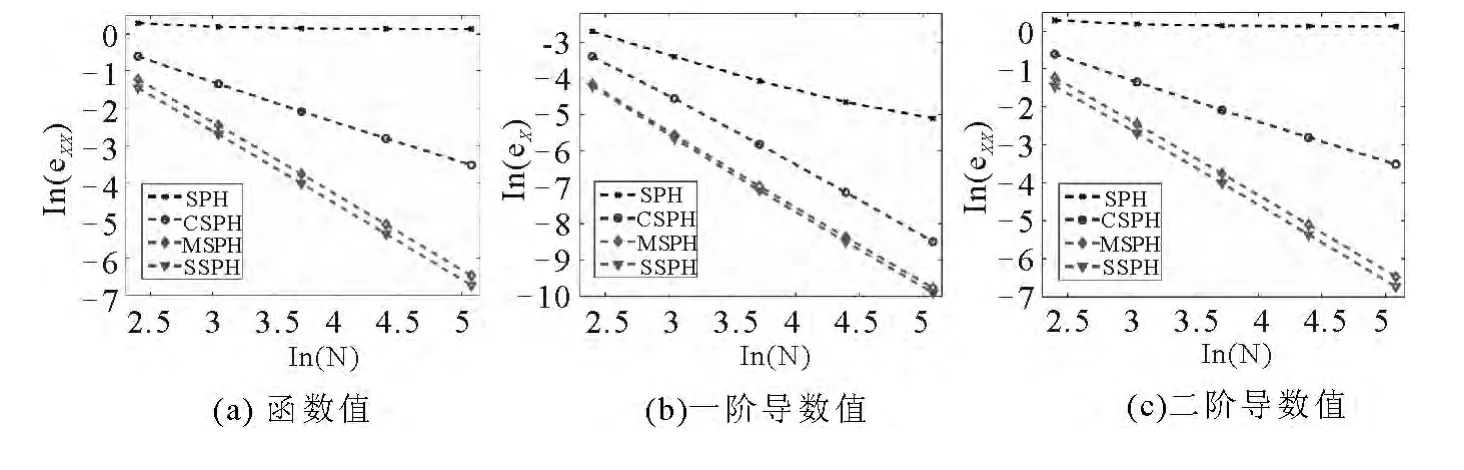
图2 一维情况误差比较

3．2 二维算例

图3给出函数 f(x，y)=sin(πx)+sin(πy)，在[0，1]×[0，1]上分别均匀分布 121，441，1681，6561，25921个粒子时，函数值和两个偏导数值误差范数进行比较，结果表明SSPH方法误差还是最小．对其它类型的f(x，y)=(0．5 － xy)4，f(x，y)=x2y2等函数及其偏导数进行了计算和比较，发现SSPH方法的精度最高．

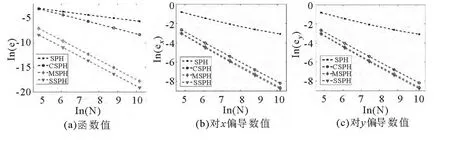
图3 二维情况误差比较

4 结论

本文对几种SPH方法进行了研究，详细介绍了每种方法在一维、二维和三维情况下核近似计算公式的推导过程．用每一种方法对一维和二维问题进行数值计算和误差比较，得出以下几个结论．

(1)用SPH方法和CSPH进行数值计算时，在边界处误差比较大，特别是在计算二阶导数时误差变得更大．用MSPH方法和SSPH进行一阶导数时，在边界处误差非常小，在边界处计算二阶导数时有明显地误差，但SSPH方法的误差比较小．

(2)用每一种方法进行误差分析，对比结果显示，误差由大到小依次排列为SPH，CSPH，MSPH，SSPH．

(3)用SSPH方法进行计算时，避免了核函数导数的计算，这样不仅提高了计算效率，而且放宽了对核函数导数的要求．

[1] R．A．Gingold＆ J．J．Monaghan;Smoothed Particle Hydrodynamics:Theory and Application to Non － Spherical Stars[J]．Mon．Not．R．Astr．Soc．1977，181:375 －389．

[2] J．J．Monaghan;Shock Simu1ation by the Particle Method SPH[J]．Computer Physics，1983，52:374 －389．

[3] L．D．Leberssky，A．G．Petschek;Smoothed Particle Hydrodyna1nics with Strength of Materials[J]．Advances in the Free Lagrange Method，Lecture Notes in Physics，1990，395:248 －257．

[4] J．K．Chen，J．E．Beraun ＆ T．C．Carney;A Corrective Smoothed Particle Method for Boundary Value Problems in Heat Conduction[J]．Comput．Methods App．Mech．Engrg．1999a，23:279－287．

[5] G．M．Zhang＆ R．C．Betra;Modified Smoothed Particle Hydrodynamics Method and Its Application to Transient Problems[J]．Computational Mechanics，2004，34:137 －146．

[6] 陈建设，徐飞，黄其青．光滑粒子流体动力学方法研究[J]．机械强度，2008，30(2):78 －82．

[7] G．M．Zhang＆ R．C．Betra;Symmetric Smoothed Particle Hydrodynamics(SSPH)Method and Its Application to Elastic Problems[J]．Computational Mechanics，2009，43:321 － 340．

[8] G．R．Liu，M．B．Liu．Smoothed Particle Hydrodynamics:A Meshless Particle Method[M]．World Scientific Publishing，2003．