基于BP 神经网络的灰度图像置乱加密方法①

2014-07-09王莉利高新成李瑞芳

佳木斯大学学报（自然科学版） 2014年4期

王莉利，高新成，李瑞芳

(1．东北石油大学计算机与信息技术学院，黑龙江大庆163318;2．东北石油大学现代教育技术中心，黑龙江大庆163318)

0 引言

数字图像是人们表达和获取信息的主要媒质之一，如何保证数字图像的传输安全一直是人们关注的重要问题．目前已经采取了许多安全措施，图像置乱加密就是其中一种，加密思想为:将图像中的像素进行变换，搅乱其原来所在的位置或颜色，将其变成一幅“杂乱无章”的图像[1]．即使图像在传输过程中被截获，也无法还原出图像的信息．

目前常用的置乱加密算法虽然能够取得较好的置乱效果，但置换规则采用穷举法容易被破解．人工神经网络是目前智能信息处理领域中一种有效的技术和方法，它可以根据样本进行自我学习，找出样本的内在规律，并根据已存储的知识对新样本进行识别，对灰度图像的置乱加密和恢复具有较好的适应性[2]．因此，本文提出了一种基于BP神经网络的置乱加密方法，利用神经网络具有的强非线性变换能力，如不给出网络变换模型，第三方很难找出关系进行破解．同时，当网络结构参数和性质参数取不同值时，置乱加密的最终效果不同;同样数字图像恢复时，所需参数亦不同，从而可较大提高图像信息的安全性．

1 常见几种数字图像置乱方法

目前，应用广泛的数字灰度图像置乱方法包括Arnold变换、Baker变换、Hilbert曲线等方法．

1．1 Arnold 变换

Arnold变换是一种常用的图像置乱技术，Arnold 变换公式的定义为[3]:

其中，(X，Y)是原图像的像素点，(X'，Y')是变换后新图像的像素点，n是图像阶数，即图像大小．利用上式，逐一对图像中的像素点进行坐标变换，当遍布了图像所有像素点之后，便产生了置乱后的图像．

1．2 Baker不倾斜

Baker变换是一种浑沌映射，能够产生非常奇妙的浑沌现象，通过Baker映射可以将图像打乱，其能量频谱分布均匀．

其中(Xk，Yk)表示某个初值经过k次映射后的值．

1．3 Hilbert 变换

Hilbert曲线是数学家David发现的一种按照走向规则填满整个正方形的分形曲线[4]．利用Hilbert曲线进行图像置乱的思想为:

(1)根据Hilbert的曲线走向规则遍历图像中所有像素点，并存入矩阵A．

(2)将A中元素进行重新排列，m为元素序号．变换公式 [(m－1)/n，(m－1)modn]．

(3)重新排列像素点，生成最终置乱图像．

1．4 三种图像置乱方法的比较

Arnold变换采用矩阵变换形式，Baker变换采用浑沌映射形式，Hilbert变换采用以按照曲线生成的矩阵与从图像中提取的像素值矩阵加密变换的形式[5]．他们都能快速地将相邻像素分散开，而且耗费的计算量很小．但这三种变换都是基于固定规则的，通过对明密文的像素直接进行比对就可发现置乱规律，在应用中很容易被破解，安全性较低．

2 BP神经网络

BP神经网络是一种具有三层或三层以上的多层神经网络，每一层都由若干个神经元组成，网络各层之间各个神经元实现前馈全连接[6]．典型的BP神经网络模型包括输入层(Input Layer)、隐层(Hide Layer)和输出层(Output Layer)，能学习和存贮大量的输入、输出之间非线性映射关系，通过不断自动调整参数，使输出误差最小．三层BP网络结构如图1所示．

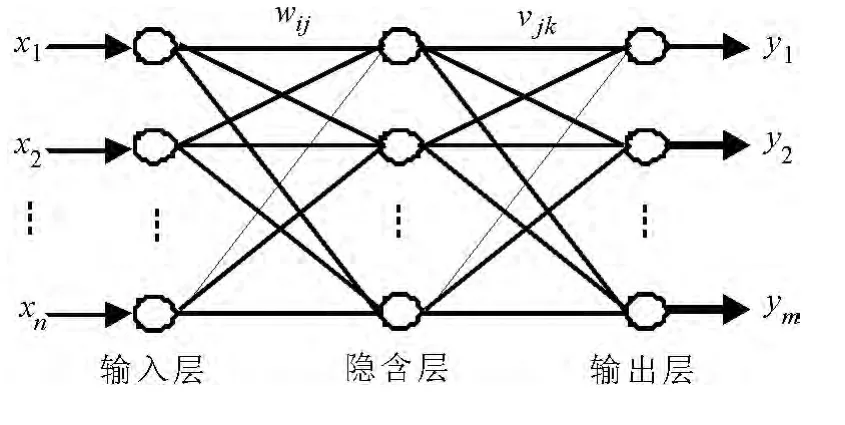
图1 三层BP网络模型

(1)(X，Y)为一维样本空间，其中X为输入样本，Y为输出样本．

(2)W为任意多层BP网络的连接权值(包括阈值)，即W=(w1，w2，…，wn)，

(3)激励函数采用Sigmoid．定义为:g(x)=1/(1+e－x)．

(4)BP算法的标准训练形式为:Wk+1=Wk－h▽E(Wk)W0=W0

其中:h＞0为学习步长．E=‖YX－Y‖2，Y为期望输出，YX为样本X的实际输出．而 ▽E(Wk)为E(Wk)在点Wk的梯度．

3 基于BP神经网络的图像置乱加密

基于BP神经网络的图像置乱加密和恢复方法:首先由一个神经网络建立原始数字图像与置乱后图像之间的变换关系，以对灰度图像进行置乱加密;再采用另一神经网络建立置乱图像与原始图像的反变换关系，以实现对置乱加密图像的恢复．基于BP神经网络的图像置乱加密算法如下:

(1)将N*M象素的原始图分成h个n*m象素的子图，取出每个子图的相应灰度值，按行排列成一维向量，作为一个输入样本．按顺序将所有的子图转换后，作为网络全部输入样本(h*n=N，h*m=M)．

(2)将N*M象素的置乱图分成h个n*m象素的子图，取出每个子图的相应灰度值，按行排列成一维向量，作为一个输出样本．按顺序将所有的子图转换后，作为网络全部输出样本(h*n=N，h*m=M)．

(3)对所有的输入和输出样本进行预处理．

(4)设置神经网络的连接权值、误差函数、计算精度和最大学习次数．

(5)利用输入和输出样本对网络进行训练．

(6)保存训练后的连接权值和阈值．

(7)将原始图片像素点的灰度值输入网络．

(8)输出即为置乱图像各个子图灰度值．

(9)根据灰度值生成子图，将子图按顺序排列，得到最终的置乱图．

图像恢复步骤同上，将置乱图像素的灰度值作为输入样本，将原始图像素的灰度值作为输出样本，提交网络进行训练，存储网络权值和阈值，即可建立置乱图与原始图之间的对应关系．

4 仿真实验

根据上述算法步骤进行置乱加密和恢复实验，训练样本的图像来源选取大小为128*128像素的灰度图像．

4．1 训练样本的获取和训练后图像的生成

实验所选取的置乱前原始图像和置乱后效果图像，如图2和图3所示．将两幅图像分别分成16个32*32像素点的子图，用Delphi中的Scanline函数分别按行取出每个子图所有像素点的灰度值．由于图像是灰度图，所以R，G，B三个分量的取值相同，取其中一个分量值作为样本元素即可，将取出的值按顺序放入定义好的二维数组中．然后按照子图的位置和顺序，用Writeln函数输出每个子图的灰度值．原始图像的灰度值即为网络的输入样本，置乱图像的灰度值即为网络的输出样本．

图2 置乱前原始图

图3 置乱后效果图

当根据训练后的样本值进行图像生成时，用read函数从输出样本中读取样本的每一个数据，分别赋予R，G，B三个分量，即可完成一个像素点的赋值．读入所有子图像素点的灰度值，生成子图并进行顺序排列，得到最终的效果图．

4．2 神经网络训练

网络选用三层BP神经网络．由于每个子图大小为32*32象素，所以设置输入、输出节点个数都为1024，中间隐层节点数设为100．样本训练个数设为16，误差为 0．05，学习速度0．08，惯性系数 0．2，采用的激励函数为Sigmoid．读入训练样本值开始训练网络，将训练后的权值和阈值进行存储，训练后收敛图如图4所示，至此建立了原始图和置乱图之间一一对应的关系．然后同样方法建立置乱图和原始图之间的对应关系．