含有负刚度夹杂复合材料稳定性问题①

王志非， 吴继华

(同济大学土木工程学院，上海200092)

0引言

复合材料中的负刚度夹杂可以提高复合材料的刚度，热膨胀，阻尼特性．很多学者研究含有负刚度夹杂的复合材料的稳定性．Lakes和Drugan［1］指出，在受到足够强的约束时，含有负刚度夹杂的复合材料是可以稳定的．为了研究含有负刚度夹杂复合材料的稳定性，Wang和 Lakes［2］引入了两种方法，分别是能量法和 Lyapunov间接方法(Lyapunov’s indirect method)．其中，Lyapunov间接方法可以用来判断动力作用下的稳定性．文献［3］介绍了低频率情况下含有负刚度夹杂粘弹性复合材料稳定性的判断准则并用FEM时程分析验证了该准则．文献［4］指出，在含有负刚度夹杂时候，常见的时程分析方法都不能无条件地保证数值稳定性．为此，本文采用Lyapunov间接方法考察含负有刚度夹杂复合材料的稳定性．

1 Lyapunov间接方法

假设动力学系统由微分方程控制

其中(1)的Jacobian矩阵J=∂X/∂x有互不相同的特征根u1，u2，…，un，那么有以下结论:如果Reu1，Reu2，…，Reun都是负的，系统是渐近稳定;如果Reu1，Reu2，…，Reun有一个是正的，系统是不稳定的;如果Reu1，Reu2，…，Reun中有至少一个是零，其余的都是负的，则系统是稳定的．

图1为一个含圆形夹杂的复合材料，中间加黑部分表示夹杂．夹杂的刚度可以为负．夹杂所占体积比由比值a/b决定．这里只考虑a/b=1/12的情况(体积比为0．545%)．根据对称性，取四分之一结构进行分析，结果如图2所示．对图2进行离散，按图3所示四种不同密度的网格进行分析．

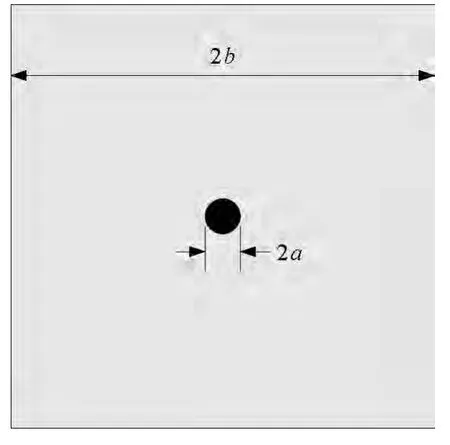
图1 含圆形夹杂的复合材料

图2 四分之一结构

用M表示质量矩阵，C表示阻尼矩阵，K表示刚度矩阵，u表示节点位移向量，f表示节点荷载向量，可以写出结构动力学方程

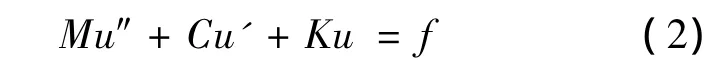
图3 四种不同密度的网格

令v=u'，将改写为

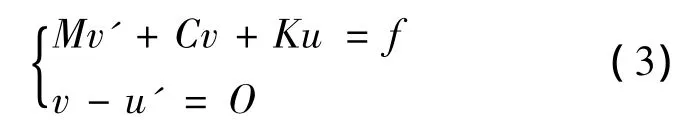
及其分块形式

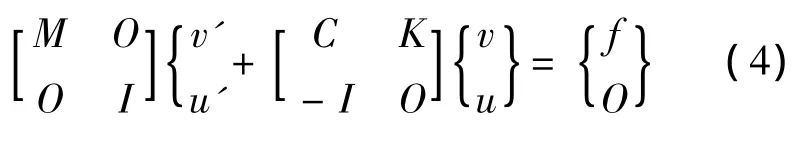
令

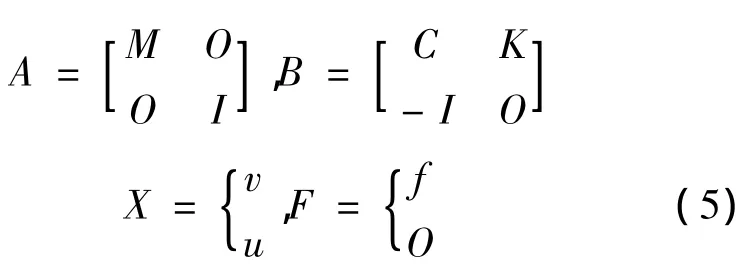
代入(4)有X'=A－1(F－BX)，此时，Jacobian矩阵如下

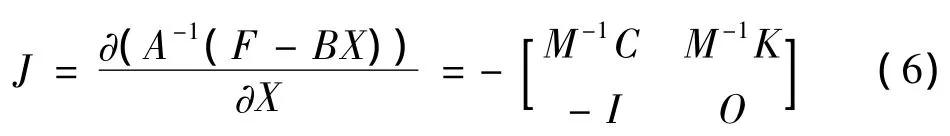
由特征方程(7)的根，可以判断该系统的稳定性．

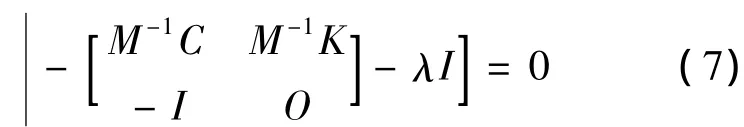
注意到(7)等价于

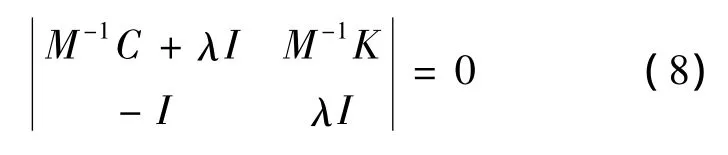
并且λ=0不是(8)的解，所以λI可逆，进而有(8)等价于

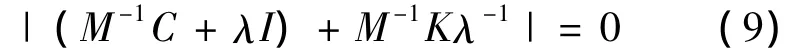
令 μ=λi，则有

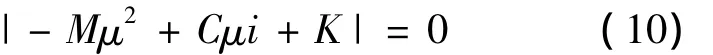
于是，Lyapunov间接方法可如此表述:

a．若方程(10)的所有根的虚部都是负的，则复合材料是渐近稳定的;

b．若存在某个根的虚部是正的，则复合材料是不稳定的;

c．若存在某个根的虚部是零，但是所有根的虚部都不是正的，则复合材料是稳定的．

若忽略阻尼C，方程(10)是实系数方程，情况a不可能存在．该复合材料只能是稳定的或不稳定的．令ω=μ2，则方程(10)可化为质量矩阵和刚度矩阵的相对特征值方程

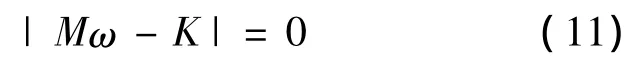
当(11)的所有根都是正实数的时候，复合材料是稳定的;只要(11)有一个负根，复合材料是不稳定的．

当阻尼C存在时，情况a可能存在，复合材料可能是渐近稳定的．

2 数值算例

考虑图1所示含有圆形刚度夹杂的正方形板，其中基体和夹杂的材料参数见表1，表中α表示夹杂的体积模量占基体体积模量之比，如α=－0．5表示夹杂的体积模量K夹杂=－0．5×130=－65GPa．

表1 材料常数

图4和图5是该复合材料在不同的α与不同的网格密度下，方程(11)的根，其中负的根用圆圈突出．图4中可以看出，α=－0．6时，含有ωn中有负值，复合材料是不稳定的．图4也说明了加密网格不一定会导致负的ωn增多;但是一般来说，负的ωn会随着网格的加密而增多，进而更好的反映出复合材料的稳定性．

图5给出了 α=－0．5130和α=－0．5134时的ωn．可以发现α=－0．5134时，复合材料是不稳定的;α=－0．5130时，复合材料是稳定的．

在α=－0．5130和 α=－0．5134之间有一个临界的αb:当α＞αb时，复合材料是稳定的;当α＜αb时，复合材料是不稳定的．

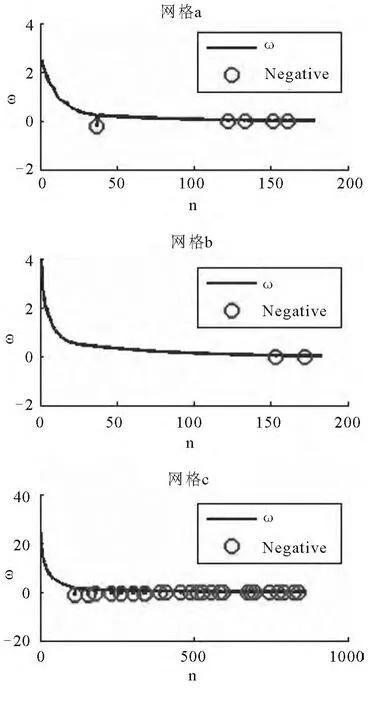
图4 α=－0．6时不同网格密度下的ωn

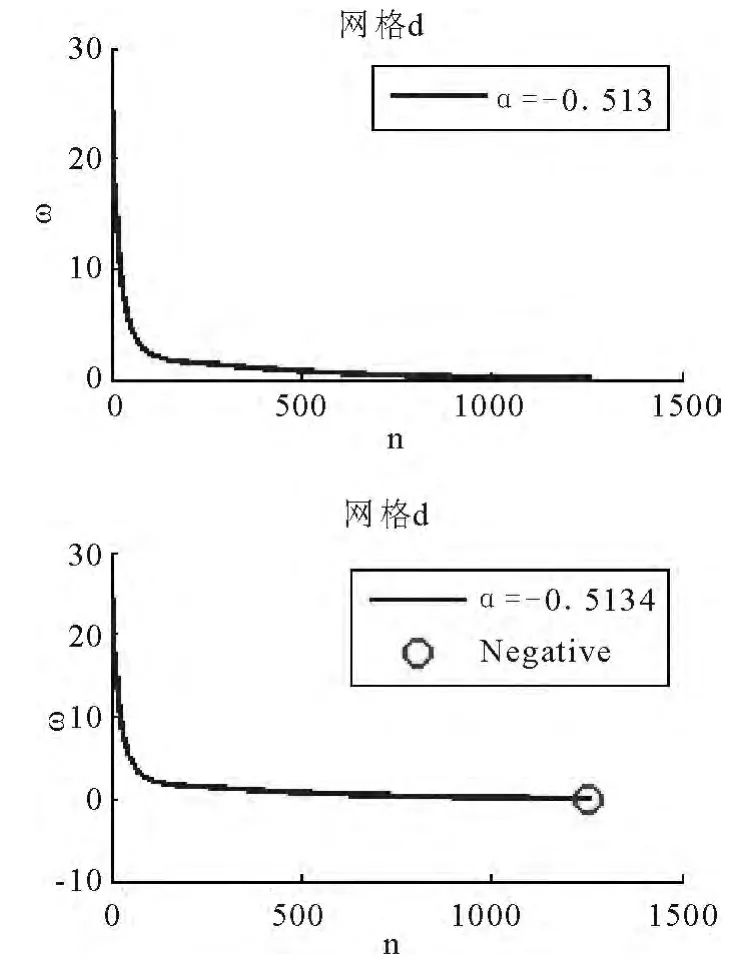
图5 α = －0．5130和 α =－0．5134

3 结 论

本文从动力学方程推导用以判断含有负刚度夹杂复合材料稳定性的Lyapunov间接方法判据．在不考虑阻尼的情况下，该判据可简化为质量矩阵和刚度矩阵相对特征值的符号．

文献[3]认为α=－0．514时，复合材料是不稳定的．本文结果与之相符，但是αb的绝对值比α=－0．514略小．这可能是因为本文不考虑阻尼作用，得到的是稳定与不稳定的界限，而文献[3]考虑阻尼作用，得到的是渐近稳定与不稳定的界限．

[1] Lakes R．S．，Drugan W．J．．Dramatically Stiffer Elastic Composite Materials Due to a Negative Stiffness Phase[J]．Journal of the Mechanics and Physics of Solids，2002，50:979 －1009．

[2] Wang Y．C．，Lakes R．S．．Stable Extremely－High －Damping Discrete Viscoelastic Systems Due to Negative Stiffness Elements[J]．Appl．Phys．Lett．，2004，84:4451 －4453．

[3] Y．C．Wang，C．C．Ko．Stability of Viscoelastic Continuum with Negative－Stiffness Inclusions in the Low－Frequency Range[J]．Phys．Status Solidi B，2013，250(10):2070 －2079．

[4] 苗启松，袁驷，陈肇元．负刚度条件下结构动力学分析的数值稳定性及一种计算方法[A]．岩土力学数值方法的工程应用——第二届全国岩石力学数值计算与模型实验学术研讨会论文集[C]．1990．