混凝土塑性损伤模型参数的研究①

陈少群

(同济大学建筑工程系，上海200092)

0 引言

K＆C模型是Malvar等[1]提出的混凝土塑性损伤模型．该模型将体积变形和形状变形分开考虑，可以考虑强化效应，拉伸和压缩损伤效应，体积变形损伤效应，应变率效应以及剪涨效应，能比较真实地反映混凝土材料的力学特性，可用于建筑结构的静态和动态分析研究．

数值模拟中混凝土材料的强度等级不同，K＆C模型强度参数的取值不同．对于强度等级相同的混凝土，K＆C模型损伤参数值取值依赖于单元尺寸[1]．然而，目前对于混凝土K＆C模型材料参数的取值，一般采用国外文献中的原始数值，或直接采用程序自动生成的参数值，并没有根据混凝土强度等级和单元尺寸的不同而对材料参数的取值做相应的调整，所以计算结果的准确性有待研究．

1 混凝土K＆C模型

K＆C模型采用初始屈服面、极限强度面和残余强度面来描述混凝土的塑性行为，它们分别表示为:

通过线性插值方法，可得到当前应力状态下混凝土的屈服面，表示为:

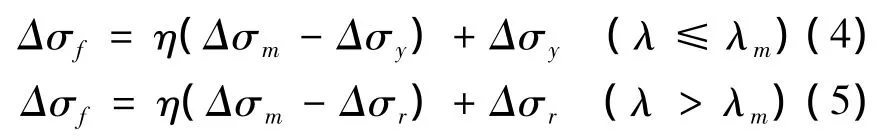
式中，η的取值是由损伤变量λ决定的，当λ从0增至λm时，η从0增至1，表示应力强化，当λ从λm增至无穷大时，η从1降为0，表示应力软化;λ是累积等效塑性应变的函数，表示为:为等效塑性应变增量，eij表示偏应变;rf为应变率效应系数;b1和b2分别为压缩和拉伸损伤参数．

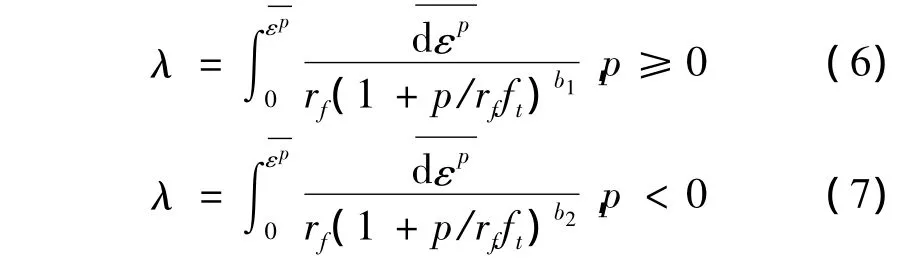
混凝土材料仅发生体积拉伸变形，即处于或近似处于三向等拉受力状态时，损伤变量λ需要考虑由体积变形引起的损伤增量Δλ，其表示为:

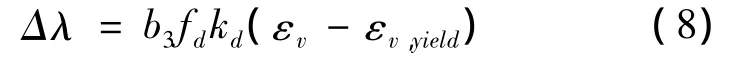
式中，b3为体积拉伸变形损伤参数;kd为一内部乘数;εv表示体积应变;εv，yield表示屈服时的体积应变;fd用于描述应力状态与三向等拉应力状态的

式中接近程度，其表达式为:

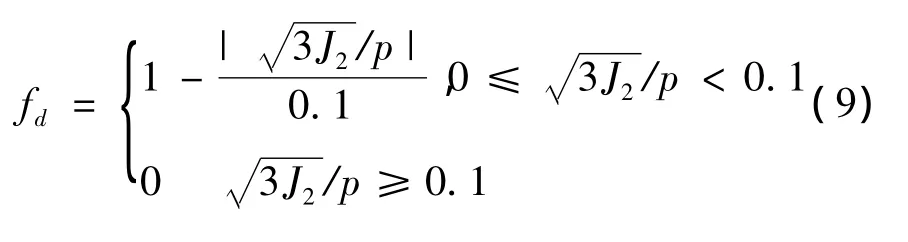
2 K＆C模型参数的确定方法

2．1 K＆C模型强度参数的确定

K＆C 模型强度参数 a0y，a1y，a2y，a0，a1，a2，a1f及a2f的确定方法主要有两种．一是利用LSDYNA程序自动生成参数的功能[2，3]，只需指定混凝土的单轴抗压强度fc，即可生成相应的强度参数值．例如，对于C40混凝土，根据我国混凝土规范，指定其单轴抗压强度fc为19．1MPa，生成的强度参数值a0，a1，a2，a0y，a1y，a2y，a1f及 a2f分别为 5．646MPa，0．446，4．23 × 10－3MPa－1，4．263MPa，0．625，1．348× 10－2MPa－1，0．442 及 6．194 × 10－3MPa－1．

方法二是对混凝土试块进行单轴压缩和不同围压下三轴压缩试验，将试验数据分别代入式(1)、(2)和(3)，从而求得相应的K＆C模型强度参数．但是，由于试验得到的数据离散性往往较高，为了使得到的强度参数比较准确，必须进行大量的试验，费用较高．因此，基于该方法的原理，本文提出一种确定 K＆C 模型强度参数 a0y，a1y，a2y，a0，a1，a2的方法，具体方法如下:

侧压相等(σ1=σ2)的混凝土三轴受压强度，美国Richart建议的直线关系式[4]为:

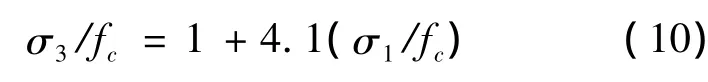
根据式(10)，分别计算单轴受压(σ1=σ2=0)和不同侧压(σ1= σ2= βfc，σ1= σ2=2βfc)下混凝土的三轴受压强度σ3，代入式(2)可求得强度参数a0，a1及a2．本文仅讨论C40混凝土，单轴抗压强度 fc为19．1MPa，分别取 β =0．6，0．7，0．8，0．9，1．0，计算得到强度参数 a0，a1及 a2分别为 8．392MPa，0．581 及 2．27 × 10－3MPa－1．

初始屈服面和极限强度面的关系如图1所示[1]，因此可确定初始屈服面的强度参数 a0y，a1y及a2y的取值．对于C40混凝土，计算得到强度参数a0y，a1y及 a2y分别为 5．676MPa，0．966 及 5．63 ×10－3MPa－1．)

2．2 K＆C模型损伤参数的确定

由LSDYNA自动生成参数法得到损伤参数b1，b2及 b3的值分别为1．65，1．35 和 1．15，不受混凝土强度和单元尺寸的影响．但是，研究表明[1]:损伤参数b1，b2及b3的取值应随混凝土单元尺寸的不同而进行调整．下面以单元边长为25mm的C40混凝土为研究对象，阐述K＆C模型损伤参数的调整方法．

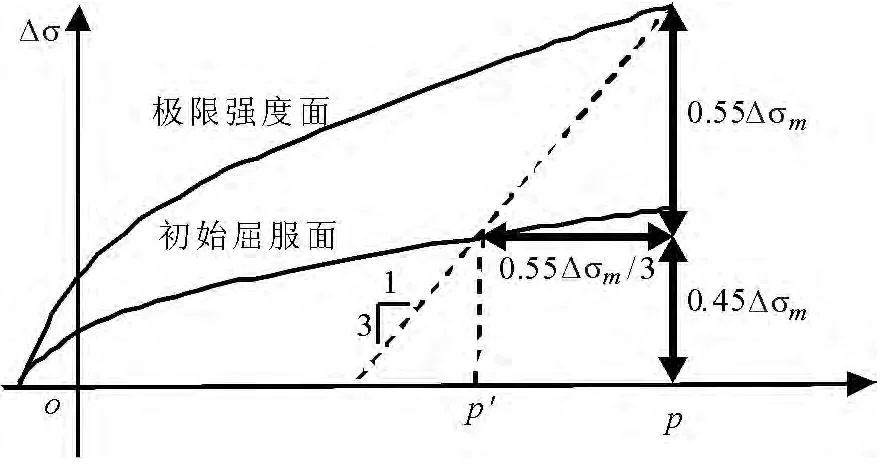
图1 初始屈服面和极限强度面

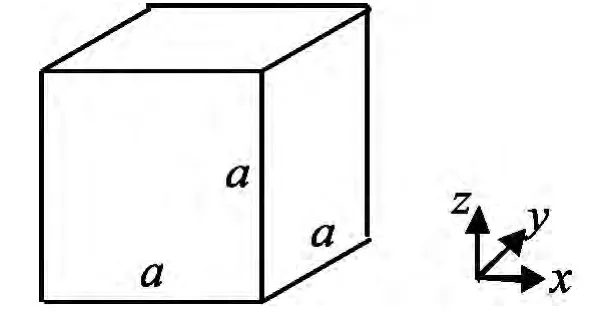
图2 单单元模型

2．2．1 压缩损伤参数b1的确定

混凝土单轴压缩试验得到极限压应变εc，u=0．004[5，6]．另外，根据我国混凝土设计规范，混凝土单轴受压的应力应变曲线可按下列公式确定:

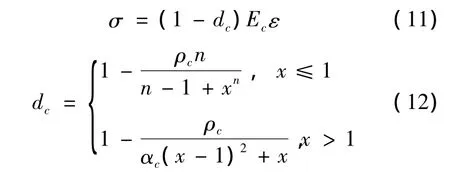
式 中:x =ε/εc，r;ρc=fc，r/Ecεc，r;n=Ecεc，r/(Ecεc，r－fc，r);αc为混凝土单轴受压应力应变曲线下降段的参数值;fc，r为混凝土的单轴抗压强度代表值;εc，r为峰值压应变;Ec为混凝土的弹性模量．对 C40 混凝土，取 αc=0．707，fc，r=fc=19．1MPa，εc，r=1．4 × 10－3及 Ec=32．5GPa．

采用常应力实体单元SOLID164建立单单元模型，如图2所示，对顶面节点施加z负向位移，并约束底面节点的所有自由度，模拟混凝土的单轴压缩试验，改变拉伸损伤参数b1的取值，得到相应的应力应变曲线，如图3所示．由图3可知，随着b1取值的减小，混凝土单轴受压应力应变曲线软化段越来越陡，极限压应变减小;b1取为1．0时得到的计算结果与规范建议的比较符合，此时混凝土的极限压应变为0．0038，与试验结果接近．

2．2．2 拉伸损伤参数b2的确定

由混凝土单轴拉伸试验得到极限拉应变εt，u=0．001[5，6]．另外，根据我国混凝土设计规范，混凝土单轴受拉的应力应变曲线可按下列公式确定:

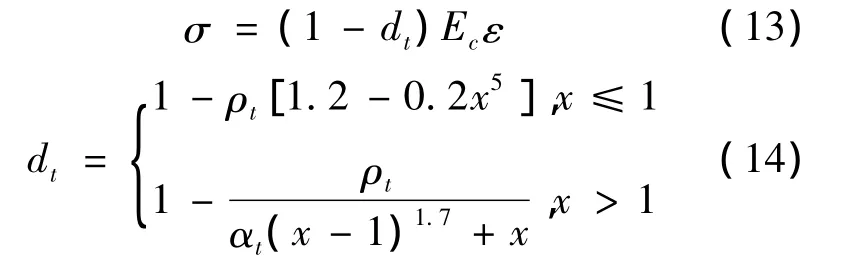
式中:x=ε/εt，r;ρt=ft，r/Ecεt，r;αt为混凝土单轴受拉应力应变曲线下降段的参数值;ft，r为混凝土的单轴抗拉强度代表值;εt，r为峰值拉应变．对C40 混凝土，取 αt=0．931，ft，r=ft=1．71MPa，εt，r=8．7×10－5．

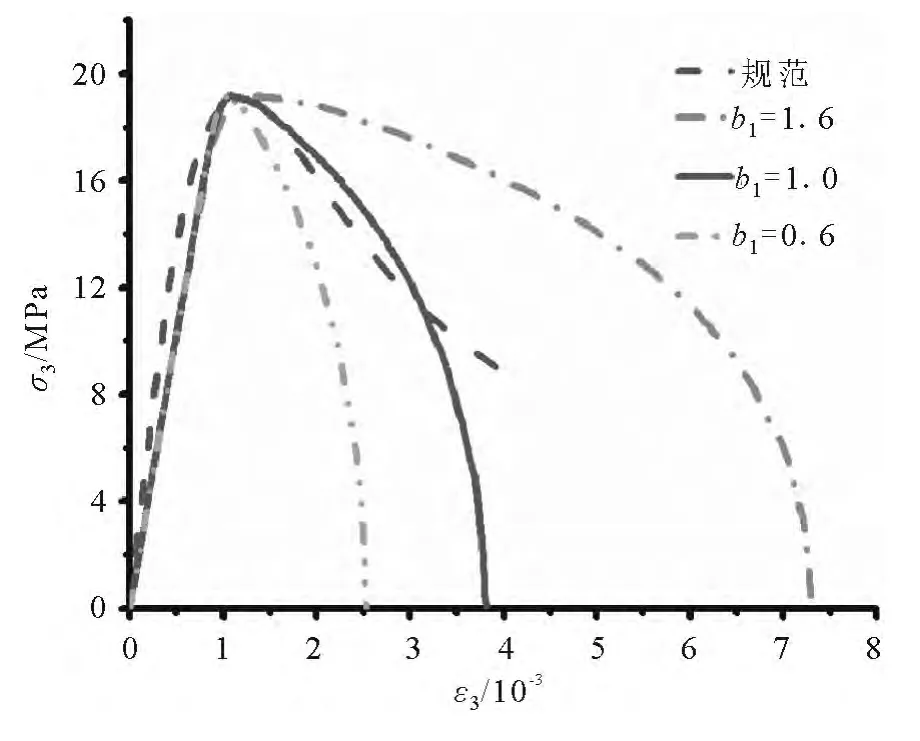
图3 混凝土单轴受压应力应变曲线

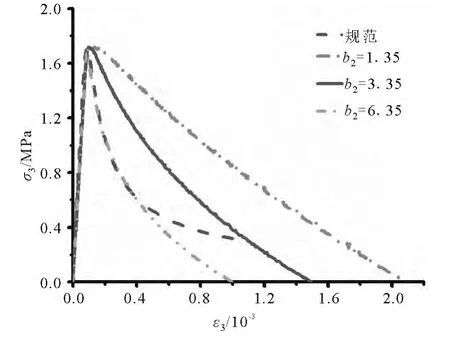
图4 混凝土单轴受拉应力应变曲线

采用常应力实体单元SOLID164建立单单元模型，如图2所示，对顶面节点施加z正向位移，并约束底面节点的所有自由度，模拟混凝土的单轴拉伸试验，改变拉伸损伤参数b2的取值，得到相应的应力应变曲线．将模拟结果与规范建议的混凝土单轴受拉应力应变曲线相比较，如图4所示．由图4可知，随着b2取值的增大，混凝土单轴受拉应力应变曲线软化段越来越陡，极限拉应变减小;b2取为6．35时得到的模拟结果与规范建议的比较符合，且极限拉应变为0．001，与试验结果相等．

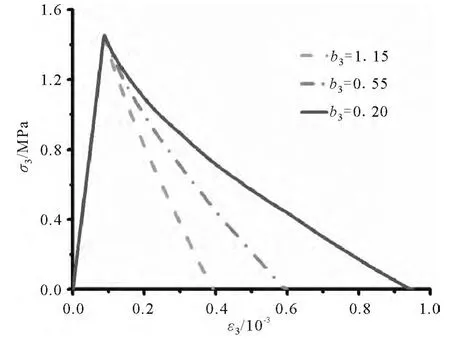
图5 混凝土三轴等拉应力应变曲线

2．2．3 体积变形损伤参数b3的确定

损伤参数b3主要影响混凝土三轴等拉应力应变曲线的软化段．对于混凝土三轴等拉试验，其强度 fttt为(0．7 ～ 1．0)ft，变形性能同单轴拉伸[7]．建立单单元模型，如图2所示，三个方向同时施加位移，模拟混凝土三轴等拉试验，改变损伤参数b3的取值，得到相应的应力应变曲线，如图5所示．由图5可知，混凝土三轴等拉强度fttt为1．45MPa，相当于0．85ft;随着损伤参数b3减小，混凝土三轴等拉应力应变曲线下降段趋于平缓，极限拉应变增大．本文取b3为0．2，此时混凝土三轴等拉的极限应变为0．00095，与单轴拉伸时混凝土的极限应变接近．

3 混凝土常规三轴压缩试验的数值模拟

如图2所示，建立25mm×25mm×25mm的单单元模型，在x和y方向上施加相等的压力(σ1=σ2)，对顶面节点施加z负向位移，并约束底面节点的所有自由度．对于C40混凝土，K＆C模型的强度参数分别取程序自动生成和本文确定的参数值，损伤参数 b1、b2及 b3的取值分别为1．0、6．35 和0．2．

采用不同的K＆C模型强度参数，模拟计算得到无侧向压力和侧向压力(σ1=σ2=0．1fc)作用下混凝土三轴压缩的应力应变曲线如图6所示．由图6可知，由于侧向压力对混凝土提供约束作用，限制混凝土的侧向变形，提高了混凝土的三轴抗压强度σ3，且塑性变形有很大发展，但采用程序自动生成的强度参数值计算得到的混凝土三轴强度σ3提高幅度较大．

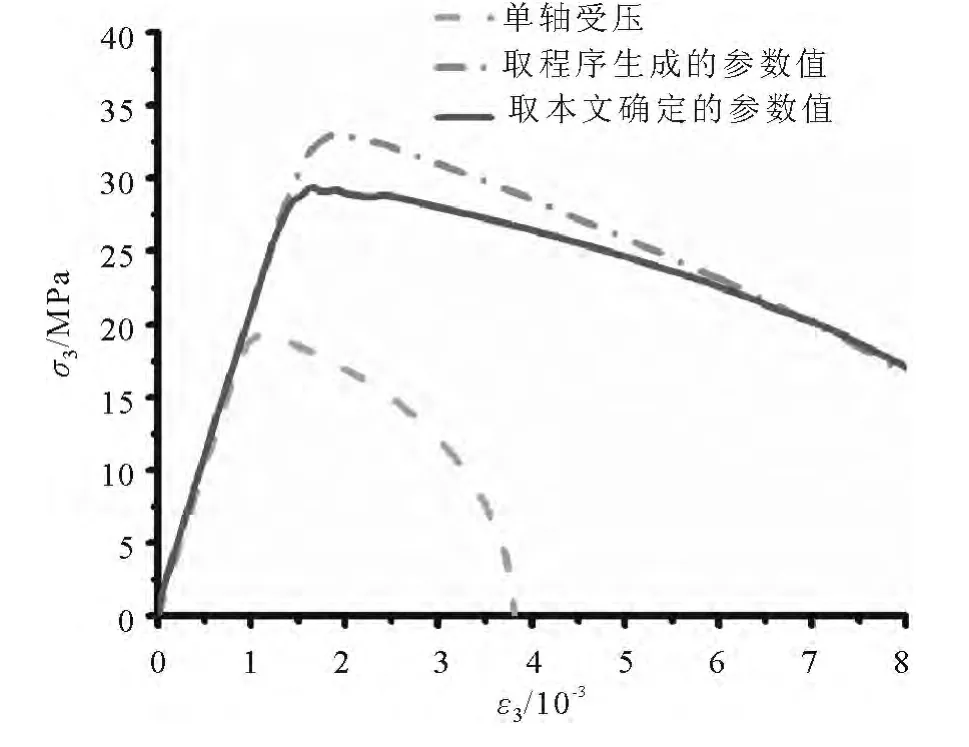
图6 混凝土常规三轴受压应力应变曲线

K＆C模型采用程序自动生成和本文确定的强度参数值，得到不同侧压下混凝土三轴抗压强度，将计算结果与国内外混凝土常规三轴压缩试验数据[4，8]进行比较，如图7 所示．由图7 可知，K＆C 模型采用本文确定的强度参数值，计算得到的混凝土三轴抗压强度与试验结果更接近;当σ1=σ2≤1．2fc时，采用程序自动生成的强度参数值，计算得到的混凝土三轴抗压强度值偏大．因此，K＆C模型的强度参数值由本文提出的方法确定更加合理．

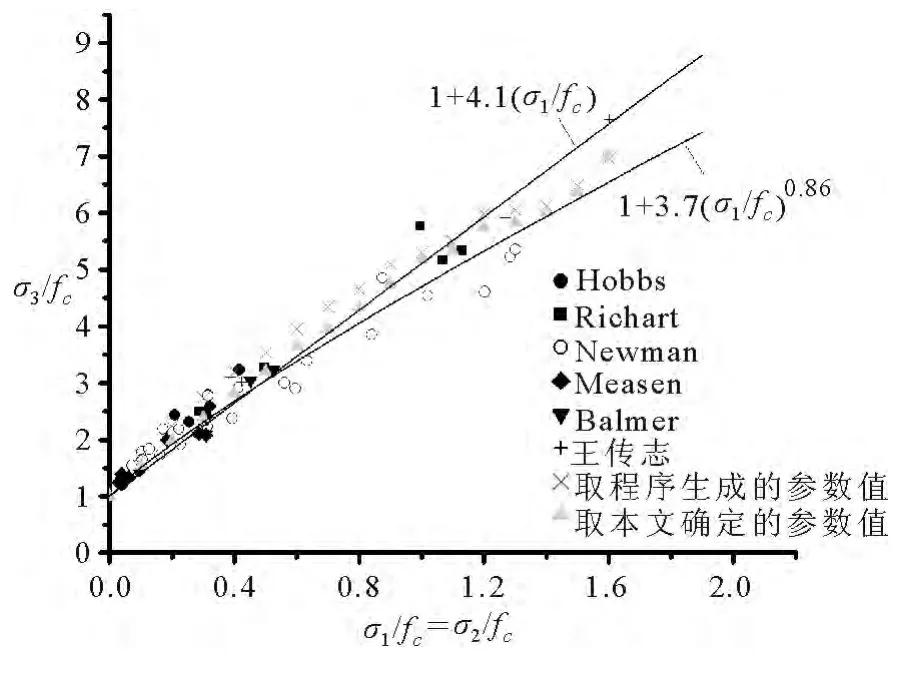
图7 混凝土常规三轴压缩极限强度

4 结 论

(1)根据混凝土常规三轴受压试验研究成果，本文提出了确定K＆C模型初始屈服面和极限强度面强度参数 a0y，a1y，a2y，a0，a1及 a2的方法．

(2)建立单单元模型，模拟单元边长为25mm的C40混凝土单轴受拉、压和三轴等拉试验，分别改变损伤参数b1，b2及b3的取值，得到相应的混凝土应力应变曲线．以规范建议的混凝土本构关系和已有的试验研究成果为基准，确定了损伤参数的取值．

(3)K＆C模型的强度参数分别取程序自动生成和本文确定的参数值，建立单单元模型，模拟混凝土的常规三轴压缩试验，并将计算结果与国内外试验结果进行比较，结果表明K＆C模型取本文确定的参数值时得到的计算结果更加合理．

[1] Malvar LJ，Crawford JE，Wesevich JW．A Plasticity Concrete Material Model for DYNA3D[J]．International Journal of Impact Engineering．1997，19(9 －10):847 －873．

[2] Hallquist，J．Q．LS － DYNA Theoretical Manual[M]．Livermore Software Technology Corporation，1988．

[3] LS－DYNA Keyword User’s Manual(970V)[M]．Livermore:Livermore Software Technology Corporation，2003．

[4] K．Newman，J．B．Newman．Failure Theories and Design Criteria for Plain Concrete．Structure Solid Mechanics and Engineering．Design，Proc．London，Wiley Inter Science，1971．

[5] 朱伯龙，董振祥．钢筋混凝土非线性分析[M]．上海:同济大学出版社，1985．

[6] 吕西林，金国方，吴晓涵．钢筋混凝土非线性有限元理论与应用[M]．上海:同济大学出版社，1997．

[7] 过镇海．钢筋混凝土原理和分析[M]．北京:清华大学出版社，2004．

[8] 王传志，过镇海，张秀琴．二轴和三轴受压混凝土的强度试验[J]．土木工程学报，1987，20(1):15－26．