基于标准系数法的空间系绳系统状态保持稳定控制*

李 超 王长青 李爱军 扎伯罗特诺夫.尤里

1.西北工业大学自动化学院国际空间系绳系统研究中心，西安 7100722.萨马拉国立航空航天大学，俄罗斯萨马拉

基于标准系数法的空间系绳系统状态保持稳定控制*

李 超1王长青1李爱军1扎伯罗特诺夫.尤里2

1.西北工业大学自动化学院国际空间系绳系统研究中心，西安 710072
2.萨马拉国立航空航天大学，俄罗斯萨马拉

首先基于哑铃模型建立空间系绳系统的数学模型，然后对标准系数法进行了介绍，在此基础上提出了基于标准系数法的空间系绳系统状态保持稳定控制算法，最后结合仿真实例对空间系绳系统的状态保持稳定控制进行了分析，并与线性最优二次型设计方法进行了比较，同时还对系统的鲁棒性进行了研究。结果表明使用标准系数法设计的控制系统不仅能够达到控制要求，而且设计简单，所得出的控制系统具有良好的鲁棒性。

标准系数法;空间系绳系统;哑铃模型;状态保持;稳定控制

空间系绳系统是指用柔性系绳将2个或2个以上的航天器连接在一起所构成的空间飞行系统［1］。自1895齐奥尔科夫斯基提出“赤道通天塔”的设想以来，美国、俄罗斯、意大利等多个国家进行了大量的研究和实验［2］。该系统具有广阔的应用前景［3-5］:从基站飞船上发射小卫星、监测高空大气层、轨道机动、依靠系绳返回舱从轨道上回收有效载荷、清理太空垃圾等。

系绳系统执行的主要科学探测活动大多是在状态保持阶段进行的。但是复杂的太空环境会给系统带来干扰，甚至会影响系统正常工作。因此，需要一定的控制策略将系统快速控制到稳定状态。Larsen等设计了一套非线性控制器，并利用电动绳注入阻尼的方法将系绳卫星系统控制到一个渐进稳定的平衡位置［6］。Mankala等设计了一套边界控制器将系统控制到径向相对平衡位置［7］。Pasca研究了系绳卫星系统在状态保持阶段的运动，并提出了利用子星推力来控制系绳的面内振荡［8］。Fujii等人在不考虑系绳的径向振动时，提出了一种波动合并控制方法来抑制系绳的横向振动［9］。国内的Yong He等通过对系统在平衡点稳定性的分析推导出了一种速率控制方法［10］。刘丽丽等研究了系绳系统在状态保持阶段的混沌运动［11］。上述文献主要针对如何将系绳系统控制到平衡位置以及研究状态保持阶段的运动。

本文采用在控制工程领域有较好应用的标准系数法［12-13］来对空间系绳系统状态保持稳定控制进行研究。它避免了复杂的优化算法，把控制系统的设计转化为简单的代数运算，大大简化了控制系统的设计。

1 模型建立

采用哑铃模型，假设系绳为刚性绳，质量不计，忽略在拉力下产生的形变，将主星和子星看作质点，主星、子星及系统总质量分别为m1，m2，m=m1+m2，并且主星质量m1远远大于子星质量m2，所以认为系统质心在主星上。在轨道坐标系下建立系统的动力学方程［14］:

为了方便研究，不考虑面外角的影响。因此系统方程(1)可以简化为

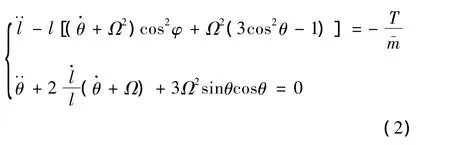
其中，T为系绳的拉力。

2 标准系数法

目前主要的标准系数法有:牛顿二项式标准型、ITAE标准型、Butterworth标准型以及各种标准型的改进型。与其他标准型相比，ITAE标准型性能指标具有较好的实用性和选择性。因此，本文选择采用ITAE标准型对空间系绳系统进行研究。

表1给出了ITAE标准型一到八阶系统的标准特征多项式的形式。其中特征参数ω0的选择具有较大的灵活性，通常是根据所要设计系统的性能要求来选择。如果事先没有给出系统的动态性能指标，ω0的选择就有较大的范围，可以根据具体情况而定。

表1 1～8阶系统的标准特征多项式

3 空间系绳系统状态保持稳定控制算法

基于标准系数法的空间系绳系统状态保持稳定控制算法如下:

1)将空间系绳系统的动力学方程进行线性化处理，得出其状态方程

把方程(2)量纲归一化，并在平衡点附近线性化得:

把系统方程写成状态空间的形式，即:

2)写出系统的开环与闭环传递函数

系绳系统的状态保持稳定控制结构图如图2所示，令C为单位矩阵。

图1 系统状态反馈结构图

系统的开环传递函数为:

系统的闭环传递函数为:

3)将开环传递函数写成分式形式

将式(5)写成如下分式形式:

代入数据，计算得系统特征多项式F(s)和分子多项式g(s)的系数矩阵F，G分别为:

4)写出闭环系统的特征方程，选取标准系数特征多项式

根据步骤2)的闭环传递函数式(6)，系统特征方程为:

将式(8)进行通分，令分子等于标准特征多项式H(s)，得到下面的关系式:

本系统为4阶系统，在表1中选取标准特征多项式H(s)，其系数矩阵H为:

5)选取ω0，求解控制器系数矩阵P

在式(9)中只有矩阵P是未知的。令关系式左右s相同指数的系数对应相等，得到一个方程组，选择适当的ω0，解方程组就可以求出控制器系数矩阵P的所有元素。

本文取ω0=1．5，求解控制器系数矩阵P的代数方程组得:

4 仿真分析

取系统的初始面内角θ=-0．1°，=0．1，系绳系统稳定保持的动态特性仿真结果如图2所示。

由图2可以看出，绳长、绳长变化率、面内角和面内角变化率都在6s内回到稳态值，此时系绳系统又稳定到平衡状态。在系统恢复到平衡状态时，虽然系统有一定的振荡，但是振荡都非常小，其最大振幅分别为 1.054，0.06，0.062，0.1665。

图2 基于标准系数法的状态保持稳定控制

4.1 与线性二次型最优控制方法的比较

针对空间系绳卫星系统在稳定状态附近的线性化模型，也可以采用线性二次型最优控制来设计控制律。在该方法中状态变量和输入变量的加权矩阵Q，R的选择非常重要。本文中取 Q=diag(5，5，30，30)，R=1，得最优化反馈增益矩阵:

在相同的摄动下，系绳系统稳定保持的动态特性仿真结果如图3所示。

图3 基于LQR方法的状态保持稳定控制

由图3可以看出，基于LQR方法设计的控制系统其绳长、绳长变化率、面内角和面内角变化率也都在6s内回到稳态值。在系统恢复到平衡状态时，系统过渡比较平稳，没有太大的振荡，其最大振幅分别为 1.083，0.102，0.031，0.149。

图4为2种设计方法控制效果比较图，其中虚线表示采用标准系数法设计的控制系统的控制效果图;实线表示采用LQR方法设计的控制系统的控制效果图。由图4可以看出，使用标准系数法设计的控制系统能够达到LQR设计方法的控制效果。

图4 2种设计方法控制效果比较

4.2 鲁棒性分析

系绳系统处于太空中，因此会受到太空碎片、极端温度等各种外界因素的影响，所以系统参数会有一定的摄动，这表现为系统方程中A，B阵的变化。当系统初始面内角为-0.1°时，研究系绳系统状态保持动态特性的鲁棒性。

图5～7分别表示A阵、B阵以及A阵和B阵同时变化±20%时系绳系统状态保持的被控变量θ的动态特性曲线。其中实线表示系统具有+20%摄动时的仿真结果，虚线表示系统没有摄动时的仿真结果，点线表示系统具有-20%摄动时的仿真结果。由图可以看出，当系统受到+20%摄动时，θ的最大振幅增加量在0.015°以内;当系统受到-20%摄动时，θ的最大振幅增加量在0.01°以内。由此可见，基于标准系数法的设计方法设计的控制系统具有良好的鲁棒性。

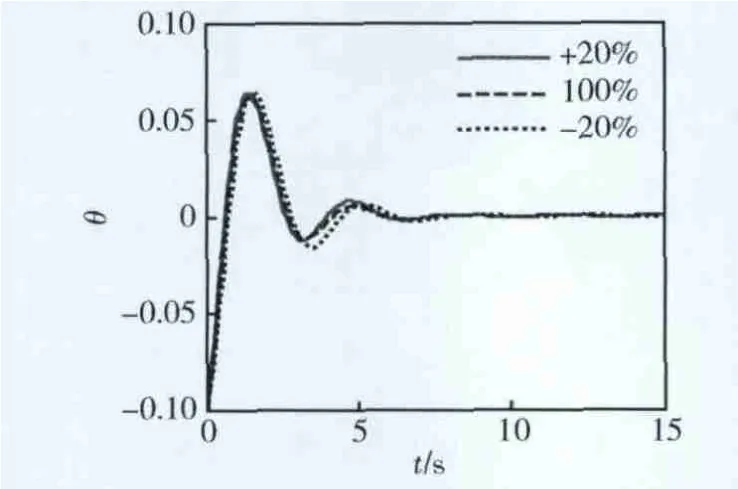
图5 A阵变化±20%时系绳系统状态保持的动态特性

5 结论

在简化的系绳系统模型下，不考虑系绳的面外运动，通过标准系数法来设计系绳系统状态保持稳定控制器。仿真结果表明这种方法与线性二次型最优化设计方法的控制效果相当，但比二次型优化设计方法简单，且得出的结果具有良好的鲁棒性。研究结果对未来空间系绳系统控制器的设计提供了一定的参考。

图6 B阵变化±20%时系绳系统状态保持的动态特性

图7 A，B阵同时变化±20%时系绳系统状态保持的动态特性

［1］孔宪仁，徐大富.空间绳系研究综述［J］.航天器环境工程，2010，27(6):0775-0783.(Kong Xianren，Xu Da fu.The Studies of Space Tether［J］.Spacecraft Environment Engineering，2010，27(6):0775-0783.)

［2］王长青，董哲，李爱军，张丛丛.空间系绳系统实验研究综述［C］.中国制导、导航与控制学术会议，北京航空航天大学，2012.(Wang Changqing，Dong Zhe，Li Aijun，Zhang Congcong.The Overview of Space Tether System Experiments［C］.Chinese Gudiance，Navigation and Control Conference，Bei Hang University，2012.)

［3］郑鹏飞，曹喜滨，张世杰.大气阻力摄动下的绳系辅助离轨系统的相对姿态跟踪控制研究［J］.航天控制，2009，27(4):8-13.(ZHENG Pengfei，CAO Xibin，ZHANG Shijie.Relative Attitude Tracking Control of Tether-assisted Deorbit System Under Drag Perturbation［J］.Aerospace Control，2009，27(4):8-13.)

［4］张玉军，冯书兴.主动式空间碎片清理研究［J］.装备指挥技术学院学报，2010，21(6):78-82.(Zhang Yujun，Feng Shuxing.Research on Active Space Debirs Removal［J］.Journal of the Academy of Equipment Control＆ Technology，2010，21(6):78-82.)

［5］冯杰，鲜勇，雷刚，魏鹏涛.绳系卫星实施安全捕获的能量最优控制［J］.航天控制，2011，29(4):66-70.(FENG Jie，XIAN Yong，LEI Gang，WEI Pengtao.Energy-optimal Control of Safe Capture by Using Tethered Subsatellite［J］.Aerospace Control，2011，29(4):66-70.)

［6］Larsen M B，Blanke M.Control by Damping Injection of Electrodynamic Tether System in an Inclined Orbit［C］.The 2009 American Control Conference，USA，2009.

［7］Mankala K K，Agrawal S K.A Boundary Controller Based on Linear Infinite Dimensional System for Station Keeping of a Tethered Satellite System［C］.The 2006 American ControlConference， Minneapolis， USA，2006.

［8］Pasca M.Nonlinear Control of Tethered Satellite System Oscillations［J］.Nonlinear Analysis:Theory，Methods and Applications，1997，30(6):3867-3878.

［9］Fujii H A，Watanabe T，Trivailo P M.Wave-absorbing Control of Transverse Vibration of Tether Systems［J］.Journal of the Astronautical Science，2003，51(3):249-259.

［10］He Yong，Liang Bin，Xu Wenfu.Study on the Stability of Tethered Satellite System ［J］.ActaAstronautica，2011，(68):1964-1972.

［11］刘丽丽，金栋平，胡海岩.状态保持阶段绳系卫星的混沌运动［C］.全国非线性振动学术会议，北京，2007.(Liu Lili，Jin Dongping，Hu Haiyang.Chaotic Oscillations of A Tethered Satellite in the Station Keeping Phase［C］.The Nonlinear Vibration of Academic Meeting，Beijing，2007.)

［12］王长青，李爱军，王伟.Butterworth滤波器在飞行控制系统中的应用［J］.飞行力学，2009，27(1):74-76.(Wang Changqin，Li Aijun，WangWei.Application of Butterworth Filter to Design of Flight Control Systems［J］.Flight Dynamics，2009，27(1):74-76.)

［13］李晋尧，张明鸣，王燕.基于ITAE的高精度无超调温度校验设备［J］.仪器仪表学报，2008，29(4):497-500.(Li Jinyao，Zhang Mingming，Wang Yan.Hight Accuracy Non-overshooting Temperature Calibrator Based on ITAE［J］.Chinese Journal of Scientific Instrument，2008，29(4):497-500.)

［14］扎伯罗特诺夫·尤里，著.空间系绳系统运动动力学与控制导论［M］.王长青，等.译.北京:科学出版社，2013.

Stability Control for Station-Keeping Phase of Space Tether System Based on Standard Coefficient Method

LI Chao1WANG Changqing1LI Aijun1ZABOLOTNOV Yuriy2
1.International Research Center of Space Tether System，College of Automation，Northwestern Polytechnical University，Xi’an 710072，China
2.Samara State Aerospace University，Samara，Russia

Firstly，the mathematical model of space tether system based on the dumbbell-shaped model is established．Then，the standard coefficient method is briefly described，and detailed discussion follows on how to design the controller．Finally，by employing simulation cases，the steady control of space tether system is analyzed，and also simulation results are given by comparing the method proposed in this paper with the well-known linear quadratic regulator method．At the same time，the robustness of the control system is studied．The simulation results show that the controller based on the standard coefficient method can achieve the requirement of control system while it is simpler than the linear quadratic regulator method and the control system also has good robustness．

Standard coefficient method;Space tether system;Dumbbell-shaped model;Station-keeping phase;Stability control

V448.2

A

1006-3242(2014)02-0073-05

*2011年度国家国际科技合作专项资助;陕西省科学技术研究发展计划项目(2013KW09-02)

2013-09-24

李 超(1986-)，男，河南鹤壁人，硕士研究生，主要研究领域为飞行器控制与仿真、空间系绳系运动动力学与控制等;王长青(1973-)，男，黑龙江富锦人，博士，副教授，主要研究领域为飞行器控制与仿真、空间系绳系统运动动力学与控制等;李爱军(1972-)，男，黑龙江密山人，博士，教授，主要研究领域为飞行器控制与仿真、空间系绳系统运动动力学与控制等;扎伯罗特诺夫·尤里(1952-)，男，俄罗斯宇航科学院院士，萨马拉国航空航天大学教授，西北工业大学高端外国专家，主要研究领域为空间系绳系统运动动力学与控制。